3137 lines
722 KiB
Plaintext
3137 lines
722 KiB
Plaintext
{
|
||
"cells": [
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "40366dea-bec8-4128-b8e9-a7c10536a613",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-44b468fb46efb002",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# 4. Programmierübung: NumPy & MatPlotLib\n",
|
||
"\n",
|
||
"<div style=\"display:flex;\">\n",
|
||
" <div style=\"text-align: left\">\n",
|
||
" Willkommen zur vierten Programmierübung Einführung in Python 3.\n",
|
||
" </div>\n",
|
||
" <img style=\"float: right; margin: 0px 15px 15px 0px\" src=\"https://www.python.org/static/img/python-logo-large.c36dccadd999.png?1576869008\" width=\"100\" />\n",
|
||
"</div>\n",
|
||
"\n",
|
||
"Wenn du Fragen oder Verbesserungsvorschläge zum Inhalt oder Struktur der Notebooks hast, dann kannst du mir gerne eine E-Mail an Phil Keier ([p.keier@hbk-bs.de](mailto:p.keier@hbk-bs.de?subject=[SigSys]%20Feedback%20Programmierübung&)) schreiben.\n",
|
||
"\n",
|
||
"Link zu einem Python Spickzettel: [hier](https://s3.amazonaws.com/assets.datacamp.com/blog_assets/PythonForDataScience.pdf)\n",
|
||
"\n",
|
||
"Der Großteil des Python-Tutorials stammt aus der Veranstaltung _Deep Learning Lab_ und von [www.python-kurs.eu](https://www.python-kurs.eu/python3_kurs.php) und wurde für _Signale und Systeme_, sowie _Einführung in die Programmierung für Nicht Informatiker_ angepasst."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "4d4eed4c-36ff-4643-bbc8-6c5440f73065",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-5ac025a1f69e3f31",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Was ist NumPy\n",
|
||
"\n",
|
||
"NumPy steht für Numerical Python, ist OpenSource und wird mittlerweile von nahezu jedem Python Entwickler eingesetzt. Dabei ist das Core Feature von NumPy seine äußerst effiziente Implementierung eines n-dimensionalen Arrays in C, welches nahtlos in Python verwendet werden kann und eine hohe Performance bei großen Datenmengen ermöglicht. Hinzu kommt eine umfassende Hülle an Funktionen wie leistungsstarke Zufallsalgorithmen sowie mathematische Routinen aus den unterschiedlichsten Bereichen der Statistik und numerischen Berechnung, welche konsequent für NumPy Arrays optimiert sind und eine intuitive, performante Datenverarbeitung erlauben. Im Folgenden wollen wir den grundlegenden sowie fortgeschrittenen Umgang mit NumPy Arrays erlernen und deren vielseitige Einsatzmöglichkeiten näher kennenlernen.\n",
|
||
"\n",
|
||
"__Für dieses Notebook schauen Sie bitte in die [NumPy Docs](https://numpy.org/doc/stable/reference/index.html)!!!__ Dort sind alle Funktionen beschrieben die wir hier bearbeiten und noch mehr!\n",
|
||
"\n",
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "ee26bbc0-d6a6-4721-b371-5cade59879ea",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-d2be4b14819d46e9",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Was ist Matplotlib\n",
|
||
"\n",
|
||
"Matplotlib ist eine leistungsfähige Python Bibliothek zum (interaktiven) Visualisieren von Daten und ermöglicht die Erstellung unterschiedlichster Diagrammtypen, von einfachen Linienplots bis hin zu komplexen wissenschaftlichen Visualisierungen. Die Bibliothek integriert sich dabei nahtlos mit anderen viel benutzten Python Bibliotheken wie NumPy und Pandas, was eine effiziente Weiterverarbeitung der Daten erlaubt. Ein besonderer Vorteil der Kombination mit Jupyter besteht in der direkten, dynamischen Ausgabe eines Plots auf dem Bildschirm, wodurch Visualisierungen unmittelbar analysiert und angepasst werden können.\n",
|
||
"\n",
|
||
"__Nutzen Sie für diese Aufgaben gerne die [Matplotlib Reference](https://matplotlib.org/stable/users/index.html).__\n",
|
||
"\n",
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "8f6a28a6-9ef0-4f80-9432-80375cf3876b",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-b8d545ee5d6cabe7",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Das gesamte Internet importiert NumPy mit dem Kürzel `np` und das pyplot Objekt mit `plt`. \n",
|
||
"\n",
|
||
"Um uns diesem ungeschriebenen Gesetz anzuschließen, importieren wir in der nächsten Zelle NumPy ebenfalls als `np` & MatPlotLib als `plt`, um eine einheitliche und leicht verständliche Schreibweise beizubehalten:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 4,
|
||
"id": "20dc6e2f-9b96-4f0c-85a8-8763e6722ce8",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3d1fe74859052932",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"import numpy as np\n",
|
||
"import matplotlib.pyplot as plt"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "57f719db-3269-49e2-acd2-a676911c0470",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-39e898b8ebe45728",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "9e008318-4d2a-4244-ac91-63d7b8806491",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-b910cff04746aa1d",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Was ist ein Array?\n",
|
||
"\n",
|
||
"Ein Array ist eine kontinuierliche Datenstruktur. Dabei werden die Daten zusammenhängend in Reihe im Arbeitsspeicher hinterlegt, vergleichbar mit der Python Liste. \n",
|
||
"\n",
|
||
"Im Gegensatz zur klassischen Liste besitzen Arrays jedoch eine feste Größe sowie einen einheitlichen Datentyp, was eine deutlich effizientere Speicherverwaltung und schnellere Verarbeitung ermöglicht. Gerade bei numerischen Operationen profitieren Arrays von ihrer strukturierten Anordnung, da Zugriffe und Berechnungen direkt und ohne zusätzlichen Overhead erfolgen können. \n",
|
||
"\n",
|
||
"Aus diesem Grund bilden Arrays die grundlegende Basis für performante Datenverarbeitung und numerische Berechnungen in Bibliotheken wie NumPy.\n",
|
||
"\n",
|
||
"\n",
|
||
"## Erstellen von Arrays\n",
|
||
"\n",
|
||
"Alle folgenden Beispiele findest du im [Beginners Guide](https://numpy.org/doc/stable/user/absolute_beginners.html).\n",
|
||
"\n",
|
||
"Für unser erstes Beispiel erstellen wir aus einer Python Liste ein [NumPy Array](https://numpy.org/doc/stable/reference/arrays.html)."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 5,
|
||
"id": "b44876d4-2376-4651-b489-9708a02f86bd",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-1adaa95f01483572",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([1, 2, 3, 4, 5])"
|
||
]
|
||
},
|
||
"execution_count": 5,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr = np.array([1,2,3,4,5])\n",
|
||
"arr"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a08e52ec-5148-4304-93da-064369cab9f8",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-ea5067ebbb1c99bc",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Der Zugriff auf Elemente des Arrays erfolgt analog zu Pythons Liste. Dabei können einzelne Werte über ihren Index adressiert werden, wobei die Zählung – wie in Python üblich – bei `0` beginnt. \n",
|
||
"\n",
|
||
"Zusätzlich ermöglichen Arrays jedoch auch den Zugriff auf ganze Bereiche mithilfe von Slicing, wodurch mehrere Elemente oder Teilabschnitte effizient und in einem Schritt ausgewählt und verarbeitet werden können."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 9,
|
||
"id": "68679f58-495f-483e-a394-0cb3016dd488",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-cb73ac88e9fa5d93",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"np.int64(5)"
|
||
]
|
||
},
|
||
"execution_count": 9,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr[4]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "97d468b2-2f23-4e8f-9b41-979ae1294754",
|
||
"metadata": {},
|
||
"source": [
|
||
"Slicing:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 7,
|
||
"id": "bd5af69f-9e56-4438-9500-5f8bbf1a50bd",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([2, 3, 4])"
|
||
]
|
||
},
|
||
"execution_count": 7,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr[1:4]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "3f9f7d47-b9d6-47b2-85e3-bdb015cc72d8",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-ec0a814ecfda8547",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"NumPy Arrays sind *n-dimensional*, das heißt Arrays in NumPy können aus geschachtelten Listen bestehen und dadurch mehrere Dimensionen abbilden. Einfache Arrays sind eindimensional, während komplexere Strukturen als zwei-, drei- oder sogar höherdimensionale Arrays vorliegen können. \n",
|
||
"\n",
|
||
"Ein klassisches Beispiel hierfür ist ein 2-dimensionales Array, das sich als Matrix interpretieren lässt und aus Zeilen und Spalten besteht. Solche Strukturen werden häufig zur Darstellung von Tabellen, Bildern oder mathematischen Matrizen verwendet und bilden die Grundlage für viele Operationen in der Datenanalyse und im Machine Learning."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 8,
|
||
"id": "04452b0d-ca06-4dd8-9b6a-47aa00b38011",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-ff72c8352626ac82",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([[1, 2, 3, 4, 5],\n",
|
||
" [6, 7, 8, 9, 8],\n",
|
||
" [7, 6, 5, 4, 3]])"
|
||
]
|
||
},
|
||
"execution_count": 8,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr = np.array(\n",
|
||
" [\n",
|
||
" [1,2,3,4,5],\n",
|
||
" [6,7,8,9,8],\n",
|
||
" [7,6,5,4,3],\n",
|
||
" ])\n",
|
||
"arr"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a4d10e8e-6856-4f14-a18c-b4d0d4cfee96",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-413fcd639649e39a",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Der Zugriff auf ein Element einer Matrix erfolgt nach dem Prinzip *\"Zeile → Spalte\"*, das heißt, zuerst wird die Zeile und dann die Spalte angegeben. \n",
|
||
"\n",
|
||
"Beispielsweise greift man in einem 2-dimensionalen Array `arr` auf das Element in der ersten Zeile und ersten Spalte mit `arr[0, 0]` zu. \n",
|
||
"\n",
|
||
"Die erste Spalte einer Matrix kann durch die Angabe aller Zeilen und der Spalte `0` ausgewählt werden, zum Beispiel mit `arr[:, 0]`, wodurch alle Elemente der ersten Spalte als neues Array zurückgegeben werden."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 9,
|
||
"id": "9539a428-4cb1-426e-9ff0-bb10f9e5dd75",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-c7a59ce293c8e402",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([1, 2, 3, 4, 5])"
|
||
]
|
||
},
|
||
"execution_count": 9,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr[0]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 10,
|
||
"id": "a7e11cb8-526f-4ded-afef-f2e2b990d3a6",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([1, 6, 7])"
|
||
]
|
||
},
|
||
"execution_count": 10,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr[:, 0]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "eb7b82f2-c8ba-4336-b3f9-505d89010e3b",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-fb0cf79581b45e5e",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Der Zugriff auf ein einzelnes Element erfolgt dann Analog:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 11,
|
||
"id": "c940ad92-43b4-4783-be50-687b2be51541",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-2f107dba2b747fbb",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"np.int64(5)"
|
||
]
|
||
},
|
||
"execution_count": 11,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr[0][4]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "37cd7d69-9a6f-4136-95bc-3470ea512f45",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-617d777cf3216789",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Oder mit NumPys eigener Syntax `arr[<spalte>, <reihe>]`"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 12,
|
||
"id": "630ba433-c2e5-4faf-980a-ae34e57d470a",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3e1e7323c57088ad",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"np.int64(5)"
|
||
]
|
||
},
|
||
"execution_count": 12,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"arr[0, 4]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "2b1ad36a-eeec-410f-82f1-768bb134accd",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-62701cdd045c7c4c",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Platzreservierung\n",
|
||
"\n",
|
||
"Falls bereits bekannt ist, wie viele Elemente ein Array im späteren Programmverlauf enthalten soll, bietet NumPy die Möglichkeit, den benötigten Speicherplatz im Voraus zu reservieren. \n",
|
||
"\n",
|
||
"Hierfür stellt NumPy verschiedene Funktionen bereit, wie zum Beispiel `np.zeros()`, `np.ones()` oder `np.empty()`. Diese Funktionen erzeugen Arrays mit einer vorgegebenen Größe, wobei die Elemente standardmäßig mit Nullen, Einsen oder undefinierten Werten initialisiert werden. Das Vorreservieren des Speichers kann die Effizienz erheblich steigern, da späteres dynamisches Erweitern des Arrays vermieden wird.\n",
|
||
"\n",
|
||
"### Ones\n",
|
||
"\n",
|
||
"1-Dimensionales NumPy Array der Größe 10 mit 1 gefüllt:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 14,
|
||
"id": "1da0eee9-4aa6-4a2e-91ab-7f9110ba5961",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-d3aeedf2a30a9b30",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])"
|
||
]
|
||
},
|
||
"execution_count": 14,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.ones(10)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "dec9de1d-0415-4ce1-8182-cdf5f50cb8cd",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-6e683d4afe40b7ff",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Zeros\n",
|
||
"\n",
|
||
"Analog dazu mit 0 gefüllt:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 15,
|
||
"id": "22b81912-0f2b-4ea6-b085-938e8f835daa",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-450f40270416767a",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])"
|
||
]
|
||
},
|
||
"execution_count": 15,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.zeros(10)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "794bfa8c-2c62-4d13-b2cf-65165b9f66d8",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-ef1e55c1165e2de5",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Empty\n",
|
||
"\n",
|
||
"Analog mit zufälligen Werten (bzw. Werte, die bereits an der Speicherstelle waren, meistens 0):"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 16,
|
||
"id": "5bede573-fda6-4065-bc05-2238cdcd7dc5",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-896e48c096be9062",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])"
|
||
]
|
||
},
|
||
"execution_count": 16,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.empty(10)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "f8543f2c-37a1-45c7-9e6f-387126d2e0c4",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-947ed3289815694d",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Arange\n",
|
||
"\n",
|
||
"Analog dazu bietet NumPy die Funktion `arange()`, die ähnlich wie die Python `range()` Funktion funktioniert. \n",
|
||
"\n",
|
||
"Mit `np.arange(start, stop, step)` kann ein Array erzeugt werden, das eine Sequenz von Zahlen von `start` bis `stop` (ausschließlich) in Schritten von `step` enthält. Im Gegensatz zu `range()` liefert `arange()` jedoch direkt ein NumPy Array, das sofort für numerische Berechnungen und Operationen genutzt werden kann."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 17,
|
||
"id": "57a83964-bf61-4db8-8358-d415d92e49bb",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-5329dd48e6129b33",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])"
|
||
]
|
||
},
|
||
"execution_count": 17,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.arange(10)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "14461c48-a442-41d8-a9dc-bd411beb6b14",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-299417e99c41e05f",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Linspace\n",
|
||
"\n",
|
||
"Um später mit Matplotlib besser arbeiten zu können, bietet NumPy die [`linspace`](https://numpy.org/doc/stable/reference/generated/numpy.linspace.html#numpy-linspace) Funktion. \n",
|
||
"\n",
|
||
"Mit `np.linspace(start, stop, num=...)` werden Werte gleichmäßig (linear) zwischen einem Start- und einem Endpunkt berechnet. Zusätzlich kann über den Parameter `num` die gewünschte Anzahl der Elemente im Array festgelegt werden. Diese Funktion ist besonders nützlich, wenn man eine feste Anzahl an Punkten für die Darstellung von kontinuierlichen Funktionen oder Graphen benötigt.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 18,
|
||
"id": "1defeafc-b02a-4e84-a1d3-30878fc69071",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-036bdec449f35dc5",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([ 0. , 2.5, 5. , 7.5, 10. ])"
|
||
]
|
||
},
|
||
"execution_count": 18,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.linspace(0,10, num=5)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 19,
|
||
"id": "72416872-9e66-4ff8-88ad-9244b6e67827",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-9ac9d3f215fc0237",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
},
|
||
"scrolled": true
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([ 400. , 466.66666667, 533.33333333, 600. ,\n",
|
||
" 666.66666667, 733.33333333, 800. , 866.66666667,\n",
|
||
" 933.33333333, 1000. ])"
|
||
]
|
||
},
|
||
"execution_count": 19,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.linspace(400, 1000, num=10)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "53cd285e-fe83-4c8b-9ac5-ee65db57107d",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-522faf35a6c76300",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe\n",
|
||
"\n",
|
||
"*1 Punkt*\n",
|
||
"\n",
|
||
"Erstelle ein NumPy Array, welches 6 Nullen reserviert und speicher das Array in der Variablen `only_zeros`. "
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 22,
|
||
"id": "8f64d227-64cc-4b26-b076-b9ea3db3d798",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-176f6befb5f45c58",
|
||
"locked": false,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"only_zeros = None\n",
|
||
"# BEGIN SOLUTION\n",
|
||
"only_zeros = np.zeros(600)\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 24,
|
||
"id": "ca435e4c-e686-4e64-b796-6f6884708ce3",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-8ad1e3a41d459d55",
|
||
"locked": true,
|
||
"points": 1,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.\n",
|
||
" 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"print(only_zeros)\n",
|
||
"\n",
|
||
"# Check i length is correct\n",
|
||
"assert len(only_zeros) == 600\n",
|
||
"\n",
|
||
"# Check if every element contains a zero\n",
|
||
"for el in only_zeros:\n",
|
||
" assert el == 0"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "07012ea7-35b0-4e24-83d4-5732853761bd",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-0108e88f3110e70f",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe\n",
|
||
"\n",
|
||
"*1 Punkt*\n",
|
||
"\n",
|
||
"Erstelle ein NumPy Array mit 11 Elementen mithilfe der Funktion `linspace`. Der Startwert soll `-6` und der Endwert `16.5` betragen.\n",
|
||
"\n",
|
||
"Speichere das Ergebnis in der Variablen `x_scale`."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 27,
|
||
"id": "41f68397-24db-44d8-a2cf-4e7aec431b57",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3231ee937ba8ab7a",
|
||
"locked": false,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"x_scale = None\n",
|
||
"# BEGIN SOLUTION\n",
|
||
"x_scale = np.linspace(-6, 16.5, num=11)\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 28,
|
||
"id": "2439440f-f8f6-4ee1-ae2b-3bca19992675",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-e5d66ef7599f7b91",
|
||
"locked": true,
|
||
"points": 1,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"[-6. -3.75 -1.5 0.75 3. 5.25 7.5 9.75 12. 14.25 16.5 ]\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"# Hier werden ihre Lösungen getestet\n",
|
||
"print(x_scale)\n",
|
||
"\n",
|
||
"# Check if length is correct\n",
|
||
"assert len(x_scale) == 11\n",
|
||
"### BEGIN HIDDEN TESTS\n",
|
||
"s = np.linspace(-6, 16.5, num=11)\n",
|
||
"### END HIDDEN TESTS\n",
|
||
"\n",
|
||
"# Test if elements are correct\n",
|
||
"for el1, el2 in zip(x_scale, s):\n",
|
||
" assert el1 == el2"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "55b7093a-9fe9-443b-a680-9f5dfc2baf41",
|
||
"metadata": {},
|
||
"source": [
|
||
"## Aufgabe\n",
|
||
"\n",
|
||
"*6 Punkte*\n",
|
||
"\n",
|
||
"Erstelle ein NumPy Array und bearbeite es anschließend wie folgt:\n",
|
||
"\n",
|
||
"1. Erzeuge ein eindimensionales NumPy Array `numbers` mit **20 gleichmäßig verteilten Zahlen** zwischen `10` und `50` mithilfe von `np.linspace`. \n",
|
||
"2. Berechne ein neues Array `squared_numbers`, das die **Quadrate** der Werte aus `numbers` enthält. \n",
|
||
"3. Finde alle Elemente in `numbers`, die **größer als 30** sind, und speichere sie in einem neuen Array `numbers_gt_30`. \n",
|
||
"4. Berechne die **Summe** aller Werte in `squared_numbers` und speichere das Ergebnis in `total_squared`. \n",
|
||
"5. Sortiere `numbers` absteigend und speichere das Ergebnis in `numbers_sorted_desc`. \n",
|
||
"6. Gebe als Kommentar die NumPy Referenz zu den verwendeten Funktionen an. (Keine Kommentare = 0 Punkte)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 89,
|
||
"id": "aa10a185-e36c-4121-91d2-7dfa913ffa63",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"array([False, False, False, False, False, False, False, False, False,\n",
|
||
" False, True, True, True, True, True, True, True, True,\n",
|
||
" True, True])"
|
||
]
|
||
},
|
||
"execution_count": 89,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"# 1. Create the NumPy array\n",
|
||
"numbers = np.linspace(10, 50, 20)\n",
|
||
"\n",
|
||
"# 2. Calculate the squares of the values\n",
|
||
"squared_numbers = numbers**2\n",
|
||
"squared_numbers = np.square(numbers)\n",
|
||
"\n",
|
||
"# 3. Find all elements greater than 30\n",
|
||
"numbers_gt_30 = numbers[numbers > 30]\n",
|
||
"\n",
|
||
"# 4. Sum all values in squared_numbers\n",
|
||
"total_squared = np.sum(squared_numbers)\n",
|
||
"\n",
|
||
"# 5. Sort in descending order\n",
|
||
"numbers_sorted_desc = np.sort(numbers)[::-1]\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 88,
|
||
"id": "464b0b7c-8209-4652-98a4-2d8b80137a7d",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"ename": "AssertionError",
|
||
"evalue": "All elements in numbers_gt_30 should be greater than 30",
|
||
"output_type": "error",
|
||
"traceback": [
|
||
"\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
|
||
"\u001b[0;31mAssertionError\u001b[0m Traceback (most recent call last)",
|
||
"Cell \u001b[0;32mIn[88], line 18\u001b[0m\n\u001b[1;32m 15\u001b[0m \u001b[38;5;28;01massert\u001b[39;00m np\u001b[38;5;241m.\u001b[39mallclose(squared_numbers, expected_squared), \u001b[38;5;124m\"\u001b[39m\u001b[38;5;124mSquared numbers are incorrect\u001b[39m\u001b[38;5;124m\"\u001b[39m\n\u001b[1;32m 17\u001b[0m \u001b[38;5;66;03m# Test 3: Check numbers_gt_30 filtering\u001b[39;00m\n\u001b[0;32m---> 18\u001b[0m \u001b[38;5;28;01massert\u001b[39;00m np\u001b[38;5;241m.\u001b[39mall(numbers_gt_30 \u001b[38;5;241m>\u001b[39m \u001b[38;5;241m30\u001b[39m), \u001b[38;5;124m\"\u001b[39m\u001b[38;5;124mAll elements in numbers_gt_30 should be greater than 30\u001b[39m\u001b[38;5;124m\"\u001b[39m\n\u001b[1;32m 19\u001b[0m \u001b[38;5;28;01massert\u001b[39;00m np\u001b[38;5;241m.\u001b[39marray_equal(numbers_gt_30, numbers[numbers \u001b[38;5;241m>\u001b[39m \u001b[38;5;241m30\u001b[39m]), \u001b[38;5;124m\"\u001b[39m\u001b[38;5;124mnumbers_gt_30 values are incorrect\u001b[39m\u001b[38;5;124m\"\u001b[39m\n\u001b[1;32m 21\u001b[0m \u001b[38;5;66;03m# Test 4: Check total_squared sum\u001b[39;00m\n",
|
||
"\u001b[0;31mAssertionError\u001b[0m: All elements in numbers_gt_30 should be greater than 30"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"# Hier werden ihre Lösungen getestet ...\n",
|
||
"\n",
|
||
"### BEGIN HIDDEN TESTS\n",
|
||
"expected_squared = numbers**2\n",
|
||
"expected_sum = np.sum(numbers**2)\n",
|
||
"expected_sorted_desc = np.sort(numbers)[::-1]\n",
|
||
"### END HIDDEN TESTS\n",
|
||
"\n",
|
||
"# Test 1: Check if numbers array has correct length and values\n",
|
||
"assert len(numbers) == 20, \"Numbers array should have 20 elements\"\n",
|
||
"assert np.isclose(numbers[0], 10), \"First element should be 10\"\n",
|
||
"assert np.isclose(numbers[-1], 50), \"Last element should be 50\"\n",
|
||
"\n",
|
||
"# Test 2: Check squared_numbers calculation\n",
|
||
"assert np.allclose(squared_numbers, expected_squared), \"Squared numbers are incorrect\"\n",
|
||
"\n",
|
||
"# Test 3: Check numbers_gt_30 filtering\n",
|
||
"assert np.all(numbers_gt_30 > 30), \"All elements in numbers_gt_30 should be greater than 30\"\n",
|
||
"assert np.array_equal(numbers_gt_30, numbers[numbers > 30]), \"numbers_gt_30 values are incorrect\"\n",
|
||
"\n",
|
||
"# Test 4: Check total_squared sum\n",
|
||
"assert np.isclose(total_squared, expected_sum), \"Sum of squared numbers is incorrect\"\n",
|
||
"\n",
|
||
"# Test 5: Check descending sort\n",
|
||
"assert np.array_equal(numbers_sorted_desc, expected_sorted_desc), \"Descending sort is incorrect\""
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "dfdb02ea-44b4-4368-9b46-235ca1dca667",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-5d8e19cc802e33a4",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "9276ba6e-30a0-4803-ace7-14147cd214ee",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-30de8243b097dfdc",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# First plot\n",
|
||
"\n",
|
||
"Wie dem [Getting Started](https://matplotlib.org/stable/users/getting_started/index.html#getting-started) Beispiel zu entnehmen ist, wollen wir die Sinus-Funktion einmal plotten. \n",
|
||
"\n",
|
||
"Dazu benötigen wir zwei Attribute: \n",
|
||
"1. **x-Skala** – Dies kann die Länge eines Datensets oder ein allgemeiner `linspace` sein. Auf jeden Fall sollte es sich um eine Liste oder ein Array handeln. \n",
|
||
"2. **y-Skala** – Im Allgemeinen die Werte des zu plottenden Datensets, ebenfalls als Liste oder Array. \n",
|
||
"\n",
|
||
"Im Folgenden plotten wir die Sinus-Funktion. Eine der schönen Eigenschaften der Sinus-Funktion ist, dass sie sich im Intervall $[0, 2\\pi]$ wiederholt. Daher enthält die x-Skala einen `linspace` von $0$ bis $2\\pi$. Als Wert für $\\pi$ verwenden wir die NumPy Konstante [np.pi](https://numpy.org/doc/stable/reference/constants.html#numpy.pi). \n",
|
||
"\n",
|
||
"Auf der y-Skala verwenden wir die zuvor berechneten Werte der Sinus-Funktion. Hierfür wird die Funktion [np.sin](https://numpy.org/doc/stable/reference/generated/numpy.sin.html) genutzt. \n",
|
||
"\n",
|
||
"Das `plt`-Objekt bietet mehrere Funktionen, die in einer bestimmten Reihenfolge aufgerufen werden müssen. Zuerst können mehrere Plots mit [plt.plot](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html) definiert werden. Zum Schluss erfolgt die Ausgabe des Plots mit [plt.show](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.show.html).\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 29,
|
||
"id": "63f7bd92-7a44-4fe0-b03e-d13b1374be1c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-2eaf77b2d04abff1",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAWWhJREFUeJzt3XlYVPXiBvD3zADDvskum4iKpoKiEi5lSaKZZVlpV0PN9GZqmd5K7q+022b7Lc2raa5l2WqZ3VDDLRVFUVxwRUE22URm2JeZ8/sDnOK6gTJ8Z3k/z3Oeex3OHN5Bc17PfBdJlmUZRERERGZEIToAERERUWtjwSEiIiKzw4JDREREZocFh4iIiMwOCw4RERGZHRYcIiIiMjssOERERGR2WHCIiIjI7FiJDiCCTqdDXl4enJycIEmS6DhERETUDLIso6ysDH5+flAobnyPxiILTl5eHgICAkTHICIioluQnZ0Nf3//G55jkQXHyckJQMMPyNnZWXAaIiIiag6NRoOAgAD9+/iNWGTBufKxlLOzMwsOERGRiWnO8BIOMiYiIiKzw4JDREREZocFh4iIiMwOCw4RERGZHRYcIiIiMjssOERERGR2WHCIiIjI7LDgEBERkdlhwSEiIiKzY9CCs2vXLowcORJ+fn6QJAk//fTTTZ+zY8cO9O7dGyqVCqGhoVi9evVV5yxevBjBwcGwtbVFVFQUkpOTWz88ERERmSyDFpyKigqEh4dj8eLFzTo/IyMDI0aMwD333IPU1FTMmjULTz/9NDZv3qw/55tvvsHs2bMxf/58HDp0COHh4YiNjUVhYaGhXgYRERGZGEmWZblNvpEkYcOGDRg1atR1z3n55Zfx66+/4vjx4/rHxo4di9LSUiQkJAAAoqKi0LdvX3z66acAAJ1Oh4CAAMycORNz585tVhaNRgMXFxeo1WruRUVERGQiWvL+bVSbbSYlJSEmJqbJY7GxsZg1axYAoLa2FikpKYiPj9d/XaFQICYmBklJSde9bk1NDWpqavS/1mg0rRucTFJ1nRYZxRXIKK5AUVkNLpXXoKZehzqtDGsrCU4qK7ja28DfzQ6B7vYIaucApeLmG7wREZF4RlVw8vPz4e3t3eQxb29vaDQaVFVV4fLly9Bqtdc859SpU9e97oIFC/Cvf/3LIJnJdFTU1GPXmSIknb+E5IwSnCkog64F9y8dbJS4o70L+gW7467OnugV6AprJcfpExEZI6MqOIYSHx+P2bNn63+t0WgQEBAgMBG1lZp6LbaeKMCGQ7n4I70YtfW6Jl93srVCqJcjfJxt4eGogp2NEkqFhLp6Hcpr6lFcXoucy5XIvFSBilotkjNKkJxRgk+3p8PV3hrDu/tiVIQf+nVwhyTx7g4RkbEwqoLj4+ODgoKCJo8VFBTA2dkZdnZ2UCqVUCqV1zzHx8fnutdVqVRQqVQGyUzGqVBTjZV7MvHNgSxcrqzTPx7czh6Du3ihb7A7ege5wsfZtlnFRKuTca6oHKlZpdidXozd6cUoqajF18lZ+Do5C528HBEXHYTRkf6wtzGq/6yIiCySUf1NHB0djf/+979NHtu6dSuio6MBADY2NoiMjERiYqJ+sLJOp0NiYiJmzJjR1nHJCF1UV2FhYjp+SMlBrbbhbo2Psy1GR7bHQxHt0cnL8ZbutCgVEjp7O6GztxMe7xsArU7G/vOX8HNqHjYdzcPZwnK8+nMaPv79LKbeFYLxdwbBQWVU/3kREVkUg/4NXF5ejvT0dP2vMzIykJqaCnd3dwQGBiI+Ph65ublYu3YtAOCZZ57Bp59+ipdeeglPPfUUtm3bhm+//Ra//vqr/hqzZ8/GhAkT0KdPH/Tr1w8ff/wxKioqMGnSJEO+FDJyZdV1+HRbOlbvzURN48dQfYLcMOWuEMR09W71wcFKhYT+oR7oH+qB/3ugK35MycGKPRnILqnCgt9O4fPdGXgxtgse7e0PBQcmExG1OYNOE9+xYwfuueeeqx6fMGECVq9ejYkTJyIzMxM7duxo8pwXXngBJ06cgL+/P1599VVMnDixyfM//fRTvP/++8jPz0dERAQWLlyIqKioZufiNHHzIcsyNh7Jw5u/nkRRWcNMuX7B7vhHbBf06+DeplnqtDr8dDgXC7edRXZJFQCge3tnvPNIT3Rv79KmWYiIzFFL3r/bbB0cY8KCYx7y1dWY++NR7DhdBKBhfM28kd1wTxcvoQN+a+q1WLM3E4sS01FWUw+lQsLkgR0w+77OsLVWCstFRGTqWHBuggXH9P2cmotXfjqOsup62FgpMPOeUEy9OwQqK+MpEEVlNfjXL2nYdPQiAKCztyM+HtML3fz4Z46I6Faw4NwEC47pqqrV4rWNafjmYDYAINzfBR88Fo5O3k6Ck13f7ycKMPfHYygur4GNUoH/G9EVcdFBnFZORNRCLDg3wYJjmrIuVWLK2oM4XVAGSQJm3hOK54Z0gpUJLLZXXF6DuT8cxe8nG/ZMGxXhh7cf6cEp5URELdCS92/jf2cgArAnvRgPLt6N0wVl8HBUYd3kKMwe2sUkyg0AeDiqsDyuD14Z0RVKhYSfUvPwyH/2Ire0SnQ0IiKzZBrvDmTR1idnIW5lMkor6xAe4IpfnxuI/qEeomO1mCRJeHpQCL56Ogoejiqcyi/DqMV7cCS7VHQ0IiKzw4JDRkuWZXy09Qzm/ngMWp2MR3q1xzdT74S3s63oaLclKqQdfpreH2E+Tigqq8GYZUnYdqrg5k8kIqJmY8Eho6TVyfjnhmNYmHgWAPDckE748PFws5lm7e9mj++eicbgLp6ortNhytoU/HgoR3QsIiKzwYJDRqdOq8Psb1PxdXI2FBKw4JEemH1fZ7ObdeRka43lcX3wcK/20OpkzP72CL7cd0F0LCIis8ApHGRU6rQ6zPzqMBLS8mGlkPDJ2F4Y0dNXdCyDsVYq8OFj4XC1t8aqPZl45afjsFJIGNsvUHQ0IiKTxoJDRkOrk/GP744gIS0fNlYKLB3fG/eGeYuOZXAKhYR5D3SDBAkr92QgfsMxKBUSHusTIDoaEZHJ4kdUZBRkWcYrPx3Dz6l5sFJIWDLOMsrNFZIk4dUHumJCdBBkGXjph6PYcJhjcoiIbhULDgknyzLe/PWkfszNv8dEYEhXyyk3V0iShNcevAPjogIhy8Ccb49g45E80bGIiEwSCw4J9+/fz2LF7gwAwDuje2JkuJ/gROJIkoQ3HuqOsX0DoJOB2d+kYvfZYtGxiIhMDgsOCfVFUqZ+KvhrI7vhcY47gUIh4e2He+DBcD/U62RM+zIFp/PLRMciIjIpLDgkzM4zRXjtlxMAgDn3dcbEAR0EJzIeCoWE9x/riX7B7iirqcekVcko0FSLjkVEZDJYcEiIMwVlmLHuELQ6GaN7+2PGvaGiIxkdlZUSy+IiEeLpgDx1NZ5afQAVNfWiYxERmQQWHGpzxeU1eGr1AZTV1KNfB3cseKSH2S3i11pc7W2wemI/tHOwQVqeBjO+OoR6rU50LCIio8eCQ22quk6LqWsPIudyFYLa2eOz8ZGwseIfwxsJbGePFRP7wtZage2ni/D2f0+JjkREZPT4zkJtRpZlxP94DIeySuFsa4WVE/vCzcFGdCyTEBHgio/HRAAAVu7J4PRxIqKbYMGhNvPlvgvYcDgXSoWEJeMj0dHTUXQkkzKsuy+eHdwRAPDy90c5s4qI6AZYcKhNpGaX4vVNDTOm4oeHYUCoh+BEpmnO0C4YGOqBqjotnvkyBZrqOtGRiIiMEgsOGdzlilpMX3cIdVoZsXd4Y/JATge/VUqFhIVP9EJ7VztkFFdgzrdHoNPJomMRERkdFhwyKJ1OxuxvU5Fb2jCo+P3Hwjlj6ja5O9hgyfjesLFSYOuJAizZeU50JCIio8OCQwa1ZOc5bD9dBJWVAv8Z1xvOttaiI5mFnv6ueOOhOwAAH245jeSMEsGJiIiMCwsOGcy+85fw4ZbTAIA3HuqOO/xcBCcyL2P6BmJ0b3/oZOCFb1KhruJ4HCKiK1hwyCDUVXWY/U0qdDIwurc/Hu/LPaYM4V8P3YGgdvbILa3C/204BlnmeBwiIoAFhwxk3s/HkaeuRlA7e7ze+FEKtT5HlRU+GdsLVgoJm45exA+HckVHIiIyCiw41Op+Ts3Fz6l5UCok/HtMBBxUVqIjmbWIAFe8cF9nAA3FMrO4QnAiIiLxWHCoVeWVVuGVn44DAGbcE4regW6CE1mGZ+7uiKgO7qis1eL59YdRx/2qiMjCseBQq9HpZMz59gjKqusREeDKHcLb0JW7Zc62VjiSo8aixLOiIxERCcWCQ61mxe4MJJ2/BDtrJf49JgLWSv7xakt+rnZ4+5EeAIDFO87heK5acCIiInHa5B1o8eLFCA4Ohq2tLaKiopCcnHzdcwcPHgxJkq46RowYoT9n4sSJV3192LBhbfFS6DrSC8vxfuOU8Hkju6GDh4PgRJbpgZ5+uL+HD7Q6GS9+fxS19fyoiogsk8ELzjfffIPZs2dj/vz5OHToEMLDwxEbG4vCwsJrnv/jjz/i4sWL+uP48eNQKpV47LHHmpw3bNiwJud9/fXXhn4pdB06nYy5PzS8md7d2RNjOSVcqNcf6g43e2ucvKjBkh1c5ZiILJPBC85HH32EKVOmYNKkSejWrRuWLl0Ke3t7rFy58prnu7u7w8fHR39s3boV9vb2VxUclUrV5Dw3Nw5mFeWLfRdw8MJlONgo8fYjPbgVg2Aejiq89mDD1PxF287i5EWN4ERERG3PoAWntrYWKSkpiImJ+fMbKhSIiYlBUlJSs66xYsUKjB07Fg4OTT/y2LFjB7y8vNClSxdMmzYNly5duu41ampqoNFomhzUOnIuV+LdhFMAgLnDw9De1U5wIgKAB8P9cF83b9TrZLz4/RHOqiIii2PQglNcXAytVgtvb+8mj3t7eyM/P/+mz09OTsbx48fx9NNPN3l82LBhWLt2LRITE/Huu+9i586dGD58OLRa7TWvs2DBAri4uOiPgAB+hNIaZFnGPzccR2WtFn2D3TAuKkh0JGokSRLeGtUdLnbWOJ6rwbJd50VHIiJqU0Y9zWXFihXo0aMH+vXr1+TxsWPH4sEHH0SPHj0watQobNq0CQcOHMCOHTuueZ34+Hio1Wr9kZ2d3Qbpzd8Ph3Kx60wRbKwUeGd0TygU/GjKmHg522L+yG4AgE9+P4tzReWCExERtR2DFhwPDw8olUoUFBQ0ebygoAA+Pj43fG5FRQXWr1+PyZMn3/T7hISEwMPDA+np6df8ukqlgrOzc5ODbk9hWTXe2HQCADArphM6ejoKTkTX8nCv9hjcxRO1Wh1e/ek496oiIoth0IJjY2ODyMhIJCYm6h/T6XRITExEdHT0DZ/73XffoaamBuPHj7/p98nJycGlS5fg6+t725mped7cdBLqqjrc4eeMKYNCRMeh65AkCa8/2B0qKwX2nruEn1PzREciImoTBv+Iavbs2Vi+fDnWrFmDkydPYtq0aaioqMCkSZMAAHFxcYiPj7/qeStWrMCoUaPQrl27Jo+Xl5fjxRdfxL59+5CZmYnExEQ89NBDCA0NRWxsrKFfDgHYm16MjUfyIEnAO4/05IJ+Ri6wnT2eG9IJAPDmryegrqwTnIiIyPAMvgvimDFjUFRUhHnz5iE/Px8RERFISEjQDzzOysqCQtH0DfL06dPYvXs3tmzZctX1lEoljh49ijVr1qC0tBR+fn4YOnQo3njjDahUKkO/HItXW6/Dqz837DU1PioIPfxdBCei5pgyKAQbDucivbAc720+hbce7iE6EhGRQUmyBX4or9Fo4OLiArVazfE4LbRkxzm8m3AK7RxssG3OYLjYW4uORM207/wljF22D5IE/DCtPzdCJSKT05L3b362QM2WW1qFhY2bOP7z/q4sNybmzpB2eKR3e8gy8H8bjqOea+MQkRljwaFme/2XNFTVadEv2B2P9G4vOg7dgn/e3xUudg3bOKxJuiA6DhGRwbDgULNsP12IzWkFUCokvD7qDm7HYKI8HFV4eVgYAODj38+guLxGcCIiIsNgwaGbqqnX4rWNaQCASf2DEebDcUumbEzfAHRv74yy6np82LgDPBGRuWHBoZtatScTFy5VwstJhVn3dRYdh26TUiFh/siGzTjXH8jG8Vy14ERERK2PBYduqKisBp9ua1gh+qVhYXBUGXxlAWoDfYPdMTLcD7IM/OuXNK5wTERmhwWHbujDLadRXlOPnv4ueKQXBxabk/jhYbC1VuBA5mVsOnpRdBwiolbFgkPXlZanxjcHGzYmnfdAN26maWb8XO0w7e5QAMCC/55EVa1WcCIiotbDgkPXJMsyXv/lBGQZeKCnL/oEu4uORAbw97tD0N7VDnnqaizdeU50HCKiVsOCQ9e0Oa0A+zNKoLJSYO7wMNFxyEBsrZX45/1dAQBLd55DXmmV4ERERK2DBYeuUlOvxdv/PQkAmHpXCPzd7AUnIkO6v4cP+gW7o6Zehw+3nBEdh4ioVbDg0FVW78lEVknDtPBn7u4oOg4ZmCRJ+OeIhrs4Px7OwYk8jeBERES3jwWHmiitrMXi7Q3Twl+M7QIHTgu3CBEBrnigpy9kGVjw20nRcYiIbhsLDjXxnx3noKmuR5iPEx7p7S86DrWhl2LDYK2U8MfZYuw6UyQ6DhHRbWHBIb3c0iqs3psJAHh5WBiUnBZuUQLb2ePJO4MBAAt+OwWtjov/EZHpYsEhvQ+3nEZtvQ53hrhjcBdP0XFIgJn3hsLJ1gonL2qw4XCu6DhERLeMBYcAACfy/nxDix/elbuFWyg3BxtMv6dh8b8Pt5xGdR0X/yMi08SCQwCA9zafgiwDI3r6IjzAVXQcEmhi/2C0d7XDRXU1Vu7JEB2HiOiWsOAQ9p4rxo7TRbBSSHhxaBfRcUgwW2sl5gxt2DV+6Y5zUFfWCU5ERNRyLDgWTpZlvPPbKQDAuKhABHs4CE5ExuChiPbo4u0ETXU9lv3BLRyIyPSw4Fi4zWn5OJqjhoONEjOHdBIdh4yEUiHp7+Ks3J2JorIawYmIiFqGBceCaXWyfmn+yQM7wMNRJTgRGZP7unkjPMAVVXVa/eKPRESmggXHgv1yJA9nC8vhbGuFyYNCRMchIyNJf47J+mp/FnK5EScRmRAWHAtVp9Xh37833L35+90d4WJnLTgRGaMBoe0QHdIOtVodFv5+VnQcIqJmY8GxUD+k5ODCpUp4ONpg0oBg0XHISEmShH/ENtzF+f5QDs4VlQtORETUPCw4FqimXouFiQ3/Gp82OBT2NtxQk64vMsgNMV29oNXJ+PfWM6LjEBE1CwuOBfp6fxby1NXwcbbFuKhA0XHIBMxpHIuz6ehFnMjTCE5DRHRzLDgWpqpWi0+3N6xrMnNIKGytlYITkSno6uuMB3r6AgA+SeRdHCIyfiw4FmZtUiaKy2sQ6G6Px/sEiI5DJuT5IZ0gScDmtAKk5alFxyEiuiEWHAtSUVOPz3adBwA8N6QTrJX87afm6+TthAd6+gEAPuGMKiIycnyHsyBf7ruAkopaBLezx6gIP9FxyAQ9PyQUkgRsOVGA47m8i0NExqtNCs7ixYsRHBwMW1tbREVFITk5+brnrl69GpIkNTlsbW2bnCPLMubNmwdfX1/Y2dkhJiYGZ8/yX5Q3Ullbj2WNd29m3NsJVrx7Q7cg1MsJI6/cxUnkf3NEZLwM/i73zTffYPbs2Zg/fz4OHTqE8PBwxMbGorCw8LrPcXZ2xsWLF/XHhQsXmnz9vffew8KFC7F06VLs378fDg4OiI2NRXV1taFfjslaty8LlypqEcS7N3Sbnmsci7OVd3GIyIgZvOB89NFHmDJlCiZNmoRu3bph6dKlsLe3x8qVK6/7HEmS4OPjoz+8vb31X5NlGR9//DFeeeUVPPTQQ+jZsyfWrl2LvLw8/PTTT4Z+OSapqlaLz3Y1zJyafk8o797QbQn1csSD4Q0l+WOOxSEiI2XQd7ra2lqkpKQgJibmz2+oUCAmJgZJSUnXfV55eTmCgoIQEBCAhx56CGlpafqvZWRkID8/v8k1XVxcEBUVdd1r1tTUQKPRNDksybr9F1BcXosAdzs83Ku96DhkBmbe2wkKCfj9JO/iEJFxMmjBKS4uhlarbXIHBgC8vb2Rn59/zed06dIFK1euxM8//4wvv/wSOp0O/fv3R05ODgDon9eSay5YsAAuLi76IyDAcqZHV9VqsXRnw9ibmfdw5hS1Dt7FISJjZ3TvdtHR0YiLi0NERATuvvtu/Pjjj/D09MRnn312y9eMj4+HWq3WH9nZ2a2Y2Lh9lZyF4vKahrs3vXn3hlrPzMaxOL+fLMCpfMu6K0pExs+gBcfDwwNKpRIFBQVNHi8oKICPj0+zrmFtbY1evXohPT0dAPTPa8k1VSoVnJ2dmxyWoLpOi6U7G8feDA7l3RtqVR09HXF/j4bVjRc3ro5NRGQsDPqOZ2Njg8jISCQmJuof0+l0SExMRHR0dLOuodVqcezYMfj6NvxF2qFDB/j4+DS5pkajwf79+5t9TUvx3cFsFJXVoL2rHR7p7S86Dpmh6YNDAQC/Hs1DRnGF4DRERH8y+D/pZ8+ejeXLl2PNmjU4efIkpk2bhoqKCkyaNAkAEBcXh/j4eP35r7/+OrZs2YLz58/j0KFDGD9+PC5cuICnn34aQMMMq1mzZuHNN9/Exo0bcezYMcTFxcHPzw+jRo0y9MsxGXVanX7szTN3h8DGindvqPV183PGkDAv6GRgyY500XGIiPSsDP0NxowZg6KiIsybNw/5+fmIiIhAQkKCfpBwVlYWFIo/33wvX76MKVOmID8/H25uboiMjMTevXvRrVs3/TkvvfQSKioqMHXqVJSWlmLgwIFISEi4akFAS7YxNQ+5pVXwcFThMe45RQY0/d5QJJ4qxI+HcvF8TGe0d7UTHYmICJIsy7LoEG1No9HAxcUFarXaLMfj6HQy7vv3TpwrqsDc4WF45u6OoiORmXti2T4knb+ECdFB+NdD3UXHISIz1ZL3b35uYYa2nMjHuaIKONtaYVxUoOg4ZAFm3NswFmf9gYZxX0REorHgmBlZlvUzWib2D4aTrbXgRGQJ+ndsh4gAV9TU6/D57vOi4xARseCYmz/OFuNYrhp21kpMHNBBdByyEJIkYcY9DXdxvky6gNLKWsGJiMjSseCYmcXbG2ay/C0qEO4ONoLTkCUZ0tULYT5OqKjVYvXeTNFxiMjCseCYkYOZJdifUQJrpYQpg0JExyELI0kSpjfexVm1JxPlNfWCExGRJWPBMSP/2dEw9ubRSH/4uHDKPLW9+3v4IsTDAeqqOny1/4LoOERkwVhwzERanhrbThVCIQF/v4vTwkkMpULCM4Mb/vwt/yMD1XVawYmIyFKx4JiJJY13b0b09EOwh4PgNGTJHu7VHu1d7VBUVoPvDlrOxrZEZFxYcMzA+aJy/HrsIgDg2cG8e0NiWSsV+PvdDWPAlv+RgXqtTnAiIrJELDhm4LOd5yHLwJAwL3T1Nb+Vmcn0PBYZADd7a2SVVCIhLV90HCKyQCw4Ji5fXY0fD+cAAJ69h3dvyDjY2SgxoX8wgCsF3OJ2hCEiwVhwTNyqvRmo08roF+yOyCB30XGI9OKig2FrrcCxXDWSzl8SHYeILAwLjgkrq67DV/uyAABT7+K6N2Rc3B1s8HjjTvaf7eT2DUTUtlhwTNj65GyU1dSjo6cD7g3zEh2H6CpPDwyBQgJ2ninCyYsa0XGIyIKw4JioOq0OK/dkAGi4e6NQSIITEV0tsJ097u/hCwBYtot3cYio7bDgmKhfjuThoroank4qjOrVXnQcouu6svDkL0fykFtaJTgNEVkKFhwTJMuy/l/DE/sHQ2WlFJyI6Pp6+Lugf8d2qNfJWLk7Q3QcIrIQLDgmaNfZYpzKL4O9jRLjo4JExyG6qb/f3XAX5+vkLKgr6wSnISJLwIJjgpbtatiWYWzfQLjYWwtOQ3Rzd3XyQJiPEyprtfiSm3ASURtgwTExx3PV2JN+CUqFhKcGBouOQ9QskiTpt29YtSeTm3ASkcGx4JiYK2NvHujpC383e8FpiJrvgZ5+8HOxRXF5DTYczhUdh4jMHAuOCcm5XKnfVJML+5GpsVYqMHlQ4yacu85Dq+P2DURkOCw4JmTF7gxodTIGhnrgDj8X0XGIWmxs3wA421rhfHEFtp4oEB2HiMwYC46JUFfW4ZsD2QB494ZMl4PKCuPvbJj5xynjRGRILDgm4sv9F1BZq0VXX2cM6uQhOg7RLZvQPxjWSgnJmSU4kl0qOg4RmSkWHBNQU6/F6r2ZAICpd3WAJHFbBjJd3s62GNnTD0DDx65ERIbAgmMCNh25iKKyGvg42+KBxjcGIlP21MAOAIBfj11EHrdvICIDYMExcrIs6/+VG9c/CNZK/paR6eve3gXRIe2g1clY03h3koioNfHd0sjtO1+CExc1sLVW4G/9AkXHIWo1Tw9quIvzVXIWymvqBachInPDgmPkrty9Gd3bH672NoLTELWee7p4IcTDAWXV9fjuYLboOERkZlhwjFhmcQUSTzWsFXJlzAKRuVAoJP2f65V7MrjwHxG1qjYpOIsXL0ZwcDBsbW0RFRWF5OTk6567fPlyDBo0CG5ubnBzc0NMTMxV50+cOBGSJDU5hg0bZuiX0eZW7cmALAP3dPFER09H0XGIWl3DnUlrZJdUYeuJfNFxiMiMGLzgfPPNN5g9ezbmz5+PQ4cOITw8HLGxsSgsLLzm+Tt27MATTzyB7du3IykpCQEBARg6dChyc5vuXTNs2DBcvHhRf3z99deGfiltSl1Vh+9ScgAAkwdyYT8yT3Y2SoyPalj47/M/OGWciFqPwQvORx99hClTpmDSpEno1q0bli5dCnt7e6xcufKa569btw7PPvssIiIiEBYWhs8//xw6nQ6JiYlNzlOpVPDx8dEfbm5uhn4pbWp9chYqa7UI83HCgNB2ouMQGUxcdBCslRIOXriMw1mXRcchIjNh0IJTW1uLlJQUxMTE/PkNFQrExMQgKSmpWdeorKxEXV0d3N3dmzy+Y8cOeHl5oUuXLpg2bRouXbp03WvU1NRAo9E0OYxZvVannzr71AAu7EfmzcvZFiPDufAfEbUugxac4uJiaLVaeHt7N3nc29sb+fnN+7z95Zdfhp+fX5OSNGzYMKxduxaJiYl49913sXPnTgwfPhxarfaa11iwYAFcXFz0R0BAwK2/qDbw2/F85Kmr4eFogwcjuLAfmb/JjYONfzuej5zLlYLTEJE5MOpZVO+88w7Wr1+PDRs2wNbWVv/42LFj8eCDD6JHjx4YNWoUNm3ahAMHDmDHjh3XvE58fDzUarX+yM427impV/4VOy4qCLbWSsFpiAzvDj8X9O/Ihf+IqPUYtOB4eHhAqVSioKCgyeMFBQXw8fG54XM/+OADvPPOO9iyZQt69ux5w3NDQkLg4eGB9PT0a35dpVLB2dm5yWGsUi5cRmp2KWyUCv2uy0SW4MrCf+uTs1FWXSc4DRGZOoMWHBsbG0RGRjYZIHxlwHB0dPR1n/fee+/hjTfeQEJCAvr06XPT75OTk4NLly7B19e3VXKLtLLx7s1DEX7wdFIJTkPUdgZ39kKIpwPKaurxfeMMQiKiW2Xwj6hmz56N5cuXY82aNTh58iSmTZuGiooKTJo0CQAQFxeH+Ph4/fnvvvsuXn31VaxcuRLBwcHIz89Hfn4+ysvLAQDl5eV48cUXsW/fPmRmZiIxMREPPfQQQkNDERsba+iXY1A5lyvx2/GLAIDJg7iwH1kWhULCpP7BAIA1ezOh48J/RHQbDF5wxowZgw8++ADz5s1DREQEUlNTkZCQoB94nJWVhYsXL+rPX7JkCWpra/Hoo4/C19dXf3zwwQcAAKVSiaNHj+LBBx9E586dMXnyZERGRuKPP/6ASmXadzzW7M2ETgYGhLZDmI/xfoxGZCiP9PaHk60VMi9VYvvpa6+VRUTUHJIsyxb3zySNRgMXFxeo1WqjGY9TXlOP6LcTUVZTj5UT++DeMO+bP4nIDL316wks/yMDA0M98OXTUaLjEJERacn7t1HPorIk3x3MRllNPUI8HTC4s5foOETCxEUHQyEBu9OLcaagTHQcIjJRLDhGQKuTsWpPJgBg0oAOUCi4sB9ZrgB3e9zXreEO5pX/LoiIWooFxwj8frIAWSWVcLGzxuje7UXHIRJu0oCGQfYbDuegtLJWcBoiMkUsOEbgysJ+f4sKhL2NleA0ROJFdXBHN19nVNfp8HWycS/MSUTGiQVHsLQ8NZIzSqBUSIiL5sJ+RAAgSRImDQgGAHyRlIl6rU5sICIyOSw4gl1Zln54dx/4utiJDUNkREaG+6Gdgw3y1NXYnFZw8ycQEf0FC45AJRW1+Ck1DwD0/1ologa21kqMiwoEAKzcw13GiahlWHAE+jo5C7X1OvRo74LegW6i4xAZnfF3BsFaKSHlwmUczSkVHYeITAgLjiB1Wh2+3HcBADCxfzAkiVPDif6Xl7MtRvRo2GOOU8aJqCVYcATZklaAi+pqeDja4IFw098klMhQrkwZ33Q0D4WaasFpiMhUsOAIsnpv49TwfoFQWSkFpyEyXuEBrugd6Io6rYwv92eJjkNEJoIFR4DjuWocyLwMK4WEcXdyajjRzTw1sOEuzlf7L6CmXis4DRGZAhYcAVY3Tg2/v4cvvJ1txYYhMgGxd/jA18UWxeW1+OXIRdFxiMgEsOC0seLyGmxsnBo+kVPDiZrFWqnAk40LYa7akwFZlgUnIiJjx4LTxtYnZ6FWq0O4vwt6BbiKjkNkMp7oGwhbawXS8jQ4kHlZdBwiMnIsOG2oTqvDF1emhg/g1HCilnBzsMHDvRo2o13Fhf+I6CZYcNpQwvF8FGhq4OGowv09ODWcqKUm9m8YbLw5LR85lysFpyEiY8aC04auDC4eF8Wp4US3oouPEwaEtoNOhv5uKBHRtbDgtJGjOaVIuXAZ1kpJv78OEbXcpMa7OOuTs1FVyynjRHRtLDht5MrdmxE9fOHFqeFEt+yeMC8EuttDXVWHn1JzRcchIiPFgtMGispqsKlx7Y6JjcvOE9GtUSokxDVOGV+9J5NTxonomlhw2sDXjVPDIwJcEcGp4US37bE+AbC3UeJ0QRmSzl8SHYeIjBALjoHV1v+5a/gkLuxH1Cpc7Kwxurc/AO4yTkTXxoJjYL8dv4jCshp4OqkwvDunhhO1lgn9Gz6m+v1kAbJLOGWciJpiwTGwK4OLx0cFwcaKP26i1hLq5YRBnTwgy8DapEzRcYjIyPAd14BSs0txOKsU1koJf+PUcKJWd+Vj3/UHslFRUy82DBEZFRYcA1rTePdmZE8/eDqpxIYhMkODO3shuJ09yqrrseEwp4wT0Z9YcAyksKwam4427Bo+oX+w2DBEZkqhkPT/fa3eyynjRPQnFhwD+Wp/Fuq0MnoHuiKcU8OJDObRSH842CiRXliOPemcMk5EDVhwDKBhangWAC7sR2RoTrbWeKxPAABg9V7uMk5EDVhwDOC/xy6iuLwG3s4qDO/uIzoOkdm7srJx4qlCXLhUITgNERmDNik4ixcvRnBwMGxtbREVFYXk5OQbnv/dd98hLCwMtra26NGjB/773/82+bosy5g3bx58fX1hZ2eHmJgYnD171pAvoUVW/WVquLWSHZLI0EI8HTG4iydkGVizl7uME1EbFJxvvvkGs2fPxvz583Ho0CGEh4cjNjYWhYWF1zx/7969eOKJJzB58mQcPnwYo0aNwqhRo3D8+HH9Oe+99x4WLlyIpUuXYv/+/XBwcEBsbCyqq6sN/XJu6nDWZRzJLoWNUoEnODWcqM1MbBxs/N3BbJRzyjiRxZNkA087iIqKQt++ffHpp58CAHQ6HQICAjBz5kzMnTv3qvPHjBmDiooKbNq0Sf/YnXfeiYiICCxduhSyLMPPzw9z5szBP/7xDwCAWq2Gt7c3Vq9ejbFjx940k0ajgYuLC9RqNZydnVvplTZ4fv1h/Jyah9G9/fHh4+Gtem0iuj6dTkbMRztxvrgCrz90B+Kig0VHIqJW1pL3b4PewamtrUVKSgpiYmL+/IYKBWJiYpCUlHTN5yQlJTU5HwBiY2P152dkZCA/P7/JOS4uLoiKirruNWtqaqDRaJochlCgqcavRxt3DefUcKI2pVBImNi48N/qvZnQ6ThlnEiEMwVl+PsXB7FP8Ea4Bi04xcXF0Gq18Pb2bvK4t7c38vPzr/mc/Pz8G55/5X9bcs0FCxbAxcVFfwQEBNzS67mZdfuzUK+T0SfIDT38XQzyPYjo+h7p7Q8nlRXOF1Xgj/Ri0XGILNLqvZnYnFagX+xWFIsYARsfHw+1Wq0/srOzDfJ9Hu3tj6cHdsDUu0IMcn0iujFHldWfU8b3cMo4UVtTV9Zhw6GGVcVFL3Jr0ILj4eEBpVKJgoKCJo8XFBTAx+fa06d9fHxueP6V/23JNVUqFZydnZschhDYzh6vPNANQ+/g1HAiUeKigyBJwPbTRThfVC46DpFF+fZgNqrqtAjzcUJUB3ehWQxacGxsbBAZGYnExET9YzqdDomJiYiOjr7mc6Kjo5ucDwBbt27Vn9+hQwf4+Pg0OUej0WD//v3XvSYRWY5gDwfc28ULALA2iVPGidqKVidjTVImgIaNcCVJEprH4B9RzZ49G8uXL8eaNWtw8uRJTJs2DRUVFZg0aRIAIC4uDvHx8frzn3/+eSQkJODDDz/EqVOn8Nprr+HgwYOYMWMGAECSJMyaNQtvvvkmNm7ciGPHjiEuLg5+fn4YNWqUoV8OEZmAK4ONvzuYjbLqOrFhiCxE4skC5Fyugqu9NR6KaC86DqwM/Q3GjBmDoqIizJs3D/n5+YiIiEBCQoJ+kHBWVhYUij97Vv/+/fHVV1/hlVdewT//+U906tQJP/30E7p3764/56WXXkJFRQWmTp2K0tJSDBw4EAkJCbC1tTX0yyEiEzAw1AOhXo5ILyzH9yk5mMQtU4gM7srdm7F9A2FrrRQbBm2wDo4xMuQ6OERkHL7YdwGv/nQcwe3ssW3OYCgUYm+XE5mzMwVlGPrvXVBIwB8v34v2rnYG+T5Gsw4OEZEoo3u3h5OtFTIvVWLnmSLRcYjM2urGKeFDu/kYrNy0FAsOEZklexsrjO3bMGV8leD1OIjM2V+nhl8Z/2YMWHCIyGzFRQdDkoBdZ4qQXsgp40SGYExTw/+KBYeIzFaAuz1iujZMaBC9qiqROfrr1PCJ/cVPDf8rFhwiMmuTGldT/eFQDtRVnDJO1Jq2nSo0qqnhf8WCQ0RmLbpjO3T2dkRlrRbfHTTMNi1Elmr13oYtUcb0DYCdjfip4X/FgkNEZk2SJEzs37AOztqkC9Byl3GiVnGmoAx70i9BIQFP3hkkOs5VWHCIyOyN6uUHFztrZJVUYvupQtFxiMzCmr9MDfd3sxcb5hpYcIjI7P11yvhqDjYmum3qyjr8aCS7hl8PCw4RWYQno4OgkIDd6cU4W1AmOg6RSfsu5c+p4XeGGM/U8L9iwSEii+DvZo+h3XwAcOE/otvx16nhE4xsavhfseAQkcW4ssrqj4dyoK7klHGiW7HtVCGyS6rgYmeNUUY2NfyvWHCIyGJEdXBHmI8Tqut0+OZglug4RCbpyuDisf2Mb2r4X7HgEJHFkCQJkxrv4qzZyynjRC11tqAMu9OLjXZq+F+x4BCRRXkooj1c7a2RW1qF308WiI5DZFKuzEK8r5u3UU4N/ysWHCKyKLbWSjzRLxAAsHpPptgwRCaktLIWPxzKAQD94pnGjAWHiCzOk3cGQamQkHT+Ek7la0THITIJ6w9ko7pOh66+zkY7NfyvWHCIyOL4udph2B0NU8Z5F4fo5uq1Oqxt/Hhq0gDjnRr+Vyw4RGSRrkwZ33A4F5crasWGITJym9MKkKeuRjsHGzwY7ic6TrOw4BCRReoT5IY7/JxRU6/D+gPcZZzoRlbtadg1fFxUIGytjXdq+F+x4BCRRWrYZTwYAPBFUibqtTqxgYiM1NGcUhy8cBnWSgnjjXxq+F+x4BCRxRoZ7gd3Bxvkqaux9QSnjBNdy6rGcWoP9PSDl7Ot2DAtwIJDRBbL1lqJvzVOGef+VERXK9RUY9PRPADQL5JpKlhwiMiijW+cMp6cUYK0PLXoOERG5ct9F1CnlREZ5Iae/q6i47QICw4RWTQfF1sM794wZXwN7+IQ6VXXabFuf8OebU8NMP6F/f4XCw4RWbxJjX95/5Sah0vlNYLTEBmHjUfycKmiFn4utoi9w1t0nBZjwSEii9c70BU9/V1QyynjRAAAWZb1g4vj+gfDSml6dcH0EhMRtbKmU8YvoI5TxsnC7c8owcmLGthaKzC2b4DoOLeEBYeICMCInr7wcLRBvqYam9PyRcchEmrl7oaF/R7p7Q9XexvBaW4NCw4REQCVlRJ/i2pYxIz7U5Ely7pUia0nG9aFmtR4Z9MUseAQETUaHxUIK4WEgxcu41gOp4yTZVqTlAlZBgZ18kAnbyfRcW6ZQQtOSUkJxo0bB2dnZ7i6umLy5MkoLy+/4fkzZ85Ely5dYGdnh8DAQDz33HNQq5v+RSNJ0lXH+vXrDflSiMgCeDnbYkRPXwDAak4ZJwtUXlOPbxsH2j810PSmhv+VQQvOuHHjkJaWhq1bt2LTpk3YtWsXpk6det3z8/LykJeXhw8++ADHjx/H6tWrkZCQgMmTJ1917qpVq3Dx4kX9MWrUKAO+EiKyFFcGG/9yJA9FZZwyTpbl+4PZKKupR4iHA+7u5Ck6zm2xMtSFT548iYSEBBw4cAB9+vQBACxatAj3338/PvjgA/j5Xb3devfu3fHDDz/of92xY0e89dZbGD9+POrr62Fl9WdcV1dX+Pj4GCo+EVmoXoFuiAhwRWp2Kb7YdwGz7+ssOhJRm9DpZKxJugAAmDggGAqFJDjR7THYHZykpCS4urrqyw0AxMTEQKFQYP/+/c2+jlqthrOzc5NyAwDTp0+Hh4cH+vXrh5UrV0KW5eteo6amBhqNpslBRHQ9Tw9quDX/5b4LqK7TCk5D1DZ2nClERnEFnGytMLq3v+g4t81gBSc/Px9eXl5NHrOysoK7uzvy85s3BbO4uBhvvPHGVR9rvf766/j222+xdetWjB49Gs8++ywWLVp03essWLAALi4u+iMgwDTn9BNR2xh2hw/au9qhpKIWGw7nio5D1CZWNE4NH9s3AA4qg33A02ZaXHDmzp17zUG+fz1OnTp128E0Gg1GjBiBbt264bXXXmvytVdffRUDBgxAr1698PLLL+Oll17C+++/f91rxcfHQ61W64/sbK5USkTXZ6VU6HdOXrE7Azrd9e8QE5mDtDw19qRfglIhYYIJTw3/qxZXtDlz5mDixIk3PCckJAQ+Pj4oLCxs8nh9fT1KSkpuOnamrKwMw4YNg5OTEzZs2ABra+sbnh8VFYU33ngDNTU1UKlUV31dpVJd83Eiout5vG8APv79LNILy7HzbBHu6eJ18ycRmagrd2+Gd/eBv5u94DSto8UFx9PTE56eNx9ZHR0djdLSUqSkpCAyMhIAsG3bNuh0OkRFRV33eRqNBrGxsVCpVNi4cSNsbW1v+r1SU1Ph5ubGEkNErcbZ1hpj+gZgxe4MrNydwYJDZqtAU41fjuQBAJ4eFCI4Tesx2Bicrl27YtiwYZgyZQqSk5OxZ88ezJgxA2PHjtXPoMrNzUVYWBiSk5MBNJSboUOHoqKiAitWrIBGo0F+fj7y8/Oh1TYM9Pvll1/w+eef4/jx40hPT8eSJUvw9ttvY+bMmYZ6KURkoSb2D4ZCAv44W4xT+ZycQOZpzd5M1Gll9A1umEFoLgw6imjdunWYMWMGhgwZAoVCgdGjR2PhwoX6r9fV1eH06dOorKwEABw6dEg/wyo0NLTJtTIyMhAcHAxra2ssXrwYL7zwAmRZRmhoKD766CNMmTLFkC+FiCxQgLs9hnf3xa/HLmLFHxl4/7Fw0ZGIWlVlbT3W7c8CYF53bwBAkm80v9pMaTQauLi46KegExFdz6Gsy3jkP3tho1Rg99x74OV084/NiUzF2qRMzPs5DUHt7LFtzmAojXztm5a8f3MvKiKiG+gd6Ibega6o1erwZeMiaETmQKuT9YOLJw/sYPTlpqVYcIiIbuLKrfsvuPAfmZHfTxbgwqVKuNhZ49FI01/Y73+x4BAR3cTQbt7wd7PD5co6/HiIC/+Refj8j/MAgHFRgbC3Mf2F/f4XCw4R0U00LPzXsH3Dit3nufAfmbzU7FIcyLwMa6X5LOz3v1hwiIia4fE+/nBSWeFcUQV2nikSHYfotly5ezMy3A/ezuY5cJ4Fh4ioGZxsrTG2X8M+dssb3xyITFHO5Ur8drxhT8inB5rX1PC/YsEhImqmiQMaZprsPXcJx3PVouMQ3ZLVezKh1ckYENoO3fzMd6kUFhwiomZq72qHB3r6AgA+28W7OGR6yqrrsP5Aw4bT5raw3/9iwSEiaoGpdzW8Kfx6NA/ZJZWC0xC1zPrkbJTX1CPUyxF3d7r5vpKmjAWHiKgF7vBzwaBOHtDJf+7ATGQKaut1+j+zUwZ1gMLMFvb7Xyw4REQt9MzdHQEA6w9koaSiVnAaoub5OTUX+ZpqeDmpMKpXe9FxDI4Fh4iohfp3bIc7/JxRXafDF9y+gUyATidjWeO4sacGdoDKSik4keGx4BARtZAkSfh7412cNUmZ3L6BjN62U4U4W1gOJ5UV/hYVKDpOm2DBISK6Bfd394G/mx1KKmrxXUqO6DhEN/TZrnMAgL/dGQhnW2vBadoGCw4R0S2wUirw9MCG7RuW7zoPLbdvICOVcqEEBzIvw0apwFONW45YAhYcIqJb9HjfALjaWyOrpBIJjSvDEhmbpTsbxt483Ku92W7LcC0sOEREt8jexgpx0cEAgGW7zkGWeReHjEt6YRm2niiAJAFT7zbvhf3+FwsOEdFtmBAdBJWVAkdy1Nh3vkR0HKImrsycuq+rNzp6OgpO07ZYcIiIbkM7RxUe6+MP4M+BnETGIF9djQ2HcwEAzwzuKDhN22PBISK6TU8PDIFCAnacLsKpfI3oOEQAgFV7MlCnldEv2B29A91Ex2lzLDhERLcp2MMBw7r7AACW7eQmnCSeuqoO6/ZnAQCeGWxZY2+uYMEhImoFV7Zv+PkIN+Ek8dbtv4Dymnp08XbCPV28RMcRggWHiKgV9PR3xaBOHtDqZCzdybE4JE51nRar9mQCAKbeFQJJMu9NNa+HBYeIqJVMvycUAPDdwRwUaKoFpyFL9X1KDorKauDrYosHI/xExxGGBYeIqJVEdXBHnyA31Gp1WL6LY3Go7dVpdViyo+EO4t/vCoG10nLf5i33lRMRtTJJkjD93oa7OOv2Z6GkolZwIrI0P6fmIbe0Ch6ONhjbzzI21bweFhwiolY0uLMnurd3RlWdFqv2ZIiOQxZEq5Pxn+3pAIApg0Jga60UnEgsFhwiolYkSRKmD264i7N6byY01XWCE5Gl+O+xizhfXAFXe2uMuzNIdBzhWHCIiFpZ7B0+CPVyRFl1Pb5IuiA6DlkAnU7Gp9sa7t48NaADHFVWghOJx4JDRNTKFAoJzzYujb9ydwaqarWCE5G5+/1kAU4XlMFJZYUJ/YNFxzEKLDhERAbwYLgfAtztcKmiFl8nZ4mOQ2ZMlmV82jj2Jq5/EFzsrAUnMg4GLTglJSUYN24cnJ2d4erqismTJ6O8vPyGzxk8eDAkSWpyPPPMM03OycrKwogRI2Bvbw8vLy+8+OKLqK+vN+RLISJqESulQr+68bJd51FbrxOciMzVrrPFOJqjhp21Ek8N6CA6jtEwaMEZN24c0tLSsHXrVmzatAm7du3C1KlTb/q8KVOm4OLFi/rjvffe039Nq9VixIgRqK2txd69e7FmzRqsXr0a8+bNM+RLISJqsUcj/eHtrEK+pho/HsoRHYfMkCzLWJR4FgDwt6hAtHNUCU5kPAxWcE6ePImEhAR8/vnniIqKwsCBA7Fo0SKsX78eeXl5N3yuvb09fHx89Iezs7P+a1u2bMGJEyfw5ZdfIiIiAsOHD8cbb7yBxYsXo7aWa04QkfFQWSkxZVDDRodLdp5DvZZ3cah17c8owcELl2GjVGDqXZa5qeb1GKzgJCUlwdXVFX369NE/FhMTA4VCgf3799/wuevWrYOHhwe6d++O+Ph4VFb+uXFdUlISevToAW9vb/1jsbGx0Gg0SEtLu+b1ampqoNFomhxERG3hb1GBcHewwYVLldh09KLoOGRmrsyceryvP7ydbQWnMS4GKzj5+fnw8mq6g6mVlRXc3d2Rn59/3ef97W9/w5dffont27cjPj4eX3zxBcaPH9/kun8tNwD0v77edRcsWAAXFxf9ERAQcKsvi4ioRextrDB5YMO4iEXbzkKrkwUnInNxKOsydqcXw0oh4e93dRQdx+i0uODMnTv3qkHA/3ucOnXqlgNNnToVsbGx6NGjB8aNG4e1a9diw4YNOHfu1nfnjY+Ph1qt1h/Z2dm3fC0iopaKiw6Cq701zhVVYNPRG39ET9Rcixvv3jzcqz0C3O0FpzE+LV4JaM6cOZg4ceINzwkJCYGPjw8KCwubPF5fX4+SkhL4+Pg0+/tFRUUBANLT09GxY0f4+PggOTm5yTkFBQUAcN3rqlQqqFQceEVEYjjZWmPKoBC8v/k0Pkk8iwd6+kGpkETHIhN2LEeNxFOFUEjAtMG8e3MtLS44np6e8PT0vOl50dHRKC0tRUpKCiIjIwEA27Ztg06n05eW5khNTQUA+Pr66q/71ltvobCwUP8R2NatW+Hs7Ixu3bq18NUQEbWNCf2DsfyP8zhfVIFfjuRhVK/2oiORCfv372cAAKMi2iPE01FwGuNksDE4Xbt2xbBhwzBlyhQkJydjz549mDFjBsaOHQs/Pz8AQG5uLsLCwvR3ZM6dO4c33ngDKSkpyMzMxMaNGxEXF4e77roLPXv2BAAMHToU3bp1w5NPPokjR45g8+bNeOWVVzB9+nTepSEio+WostLPqFqYyLE4dOsOZ13GtlOFUCokzBzSSXQco2XQdXDWrVuHsLAwDBkyBPfffz8GDhyIZcuW6b9eV1eH06dP62dJ2djY4Pfff8fQoUMRFhaGOXPmYPTo0fjll1/0z1Eqldi0aROUSiWio6Mxfvx4xMXF4fXXXzfkSyEium0T+gfDzd4a54srsPFIrug4ZKL+/XvDujcP92qPDh4OgtMYL0mWZYv7Z4RGo4GLiwvUanWTNXaIiAztPzvS8V7CaYR4OGDLC3fBSskdc6j5Ui6UYPSSJCgVErbPGYzAdpY1uLgl79/8L4uIqA3FRf/1Lg5nVFHL/Htrw92bxyL9La7ctBQLDhFRG3JUWWFq45oli7alc3Vjarb95y/p172Zfk+o6DhGjwWHiKiNxUUHwd3BBhnFFfjxEMfiUPNcmTn1eN8ArnvTDCw4RERtzEFlhWcb1y75+PczqKnXCk5Exm7vuWLsO18CG6WCd2+aiQWHiEiA8XcGwdfFFnnqany1P0t0HDJisizjg82nAQBj+gagvaud4ESmgQWHiEgAW2slnmtcw2Tx9nRU1NQLTkTG6veThTiUVQpbawVm3su7N83FgkNEJMijkf4IbmeP4vJarN6bKToOGSGt7s+7N5MGdIAXdwxvNhYcIiJBrJUKvHBfZwDA0p3noK6sE5yIjM3GI7k4XVAGZ1srPMMdw1uEBYeISKCRPf0Q5uOEsup6fLbrnOg4ZERq63X4aGvDzKlnBneEi7214ESmhQWHiEgghULCnKFdAACr9mSisKxacCIyFusPZCG7pApeTipM6t9BdByTw4JDRCRYTFcvRAS4oqpOi0WJ6aLjkBGorK3HwsY/CzOHdIKdjVJwItPDgkNEJJgkSXh5WBgA4OvkLJwvKheciERbtScTxeU1CGpnj7F9A0THMUksOERERiC6YzvcG+aFep2M9xJOi45DAl2uqMXSnQ3jsWbf1xnW3JD1lvCnRkRkJOYOD4NCAhLS8nEws0R0HBLkk8SzKKuuR1dfZ4zs6Sc6jsliwSEiMhKdvZ3weJ+GjyPe/u9JyLIsOBG1tYziCny57wIA4JURXaFQSIITmS4WHCIiI/LCfZ1hZ63EoaxSJBzPFx2H2tg7v51EvU7GPV08MSDUQ3Qck8aCQ0RkRLydbTFlUMOU4HcTTqFOqxOciNpKckYJNqcVQCEB/7y/q+g4Jo8Fh4jIyEy9uyM8HG2QeamSG3FaCJ1Oxlu/ngAAjO0XiE7eToITmT4WHCIiI+OossLzMQ1bOHySeBaaam7hYO5+OZqHIzlqONgo8ULj7z3dHhYcIiIjNLZvADp6OqCkohaLEs+KjkMGVF2n1S8NMG1wR3g6qQQnMg8sOERERshaqcCrD3QD0LDo2zku/me2Vu3JRG5pFXycbTF5YIjoOGaDBYeIyEgN7uKlX/zvzU0nRMchAyjQVOPTbQ136F6M7cItGVoRCw4RkRF7ZURXWCslbD9dhO2nCkXHoVb2zm+nUFGrRa9AVzzcq73oOGaFBYeIyIiFeDpi0oCGaeNvbDqB2npOGzcXBzNLsOFwLiQJeG3kHVzUr5Wx4BARGbmZ94bCw9EG54srsDYpU3QcagVanYz5G9MAAI9HBiA8wFVsIDPEgkNEZOScbK3xUmzDbuOf/H4WxeU1ghPR7frmQDbS8jRwsrXCi8O6iI5jllhwiIhMwKOR/ujR3gVlNfV4L+GU6Dh0G9SVdXh/c8Pv4QsxneHhyGnhhsCCQ0RkAhQKCa89eAcA4NuDOTjA3cZN1kdbT+NyZR06ezviyegg0XHMFgsOEZGJiAxywxP9GnYb/78Nx7hPlQlKy1Pji8bdwl8beQeslXwbNhT+ZImITMjLw8Lg7mCDMwXlWLE7Q3QcagGtTkb8j8egk4ERPX3Rn7uFGxQLDhGRCXG1t9HvNP3J72eRc7lScCJqri+SMnE0Rw0nWyvMb1ylmgzHoAWnpKQE48aNg7OzM1xdXTF58mSUl19/ufHMzExIknTN47vvvtOfd62vr1+/3pAvhYjIaIzu3R5RHdxRVafFaxu5wrEpuKiuwvubG/abenlYGLycbQUnMn8GLTjjxo1DWloatm7dik2bNmHXrl2YOnXqdc8PCAjAxYsXmxz/+te/4OjoiOHDhzc5d9WqVU3OGzVqlCFfChGR0ZAkCW893B3WSgm/nyzAlrR80ZHoJl7bmIaKWi16B7rib/0CRcexCFaGuvDJkyeRkJCAAwcOoE+fPgCARYsW4f7778cHH3wAPz+/q56jVCrh4+PT5LENGzbg8ccfh6OjY5PHXV1drzqXiMhShHo5YcqgEPxnxzm8tjENA0I94KAy2F/pdBu2pOVjc1oBrBQSFjzSkysWtxGD3cFJSkqCq6urvtwAQExMDBQKBfbv39+sa6SkpCA1NRWTJ0++6mvTp0+Hh4cH+vXrh5UrV0KW5etep6amBhqNpslBRGTqZt7bCQHudshTV+Ndro1jlMpr6vUrFk+9KwRdfJwEJ7IcBis4+fn58PLyavKYlZUV3N3dkZ/fvNupK1asQNeuXdG/f/8mj7/++uv49ttvsXXrVowePRrPPvssFi1adN3rLFiwAC4uLvojICCg5S+IiMjI2Nko8c4jPQEAa5MuIOncJcGJ6H99sPk0LqqrEehuj+eGdBIdx6K0uODMnTv3ugOBrxynTt3+vySqqqrw1VdfXfPuzauvvooBAwagV69eePnll/HSSy/h/fffv+614uPjoVar9Ud2dvZt5yMiMgYDQj3wROOYjpd/OIrK2nrBieiKpHOXsHpvJgDgrYe7w9ZaKTaQhWnxB7Zz5szBxIkTb3hOSEgIfHx8UFhY2OTx+vp6lJSUNGvszPfff4/KykrExcXd9NyoqCi88cYbqKmpgUp19ZLXKpXqmo8TEZmDf94fhp2nC5FVUon3N5/G/JF3iI5k8Spq6vHi90cAAE/0C8SgTp6CE1meFhccT09PeHre/DcqOjoapaWlSElJQWRkJABg27Zt0Ol0iIqKuunzV6xYgQcffLBZ3ys1NRVubm4sMURkkZxsrbFgdE9MWJmM1XszcX8PX/QNdhcdy6K9/d+TyLlchfaudvi/EV1Fx7FIBhuD07VrVwwbNgxTpkxBcnIy9uzZgxkzZmDs2LH6GVS5ubkICwtDcnJyk+emp6dj165dePrpp6+67i+//ILPP/8cx48fR3p6OpYsWYK3334bM2fONNRLISIyend39sTjffwhy8BL3x9FVa1WdCSL9cfZIqzbnwUAeP/RnnDk7DYhDLoOzrp16xAWFoYhQ4bg/vvvx8CBA7Fs2TL91+vq6nD69GlUVjZdiXPlypXw9/fH0KFDr7qmtbU1Fi9ejOjoaEREROCzzz7DRx99hPnz5xvypRARGb3/G9EN3s4qZBRX4IMtp0XHsUia6jq8/P1RAEBcdBC3YxBIkm80v9pMaTQauLi4QK1Ww9nZWXQcIqJWs/1UISatPgAA+GJyP479aGMvfX8E3x7MQaC7PRJmDYK9De/etKaWvH9zLyoiIjNyT5gXnrwzCAAw+9sjuFReIziR5diSlo9vD+ZAkoAPHgtnuRGMBYeIyMz834iu6OTliKKyGrz8w9EbLoRKrSOvtAovNn409fTADujXgYO8RWPBISIyM7bWSix8ohdslAr8frIQX+67IDqSWavX6vD8+sNQV9Whp78LXowNEx2JwIJDRGSWuvo64+XhDW+0b/56EmcKygQnMl8Lt6XjQOZlOKqssOiJXrCx4lurMeDvAhGRmZrUPxh3d/ZETb0Oz319GNV1nDre2vadv4RPt50F0LBacVA7B8GJ6AoWHCIiM6VQSPjgsXC0c7DBqfwyzPv5OMfjtKLLFbWYtT4VOhl4NNIfD0W0Fx2J/oIFh4jIjHk6qfDJ2F5QSMC3B3Ow/gD34msNWp2M2d+mIl9TjRBPB/zrQW6PYWxYcIiIzNzATh6YM7QLAGD+z2lIzS4VG8gM/HvrGWw/XQSVlQKLnugFB65WbHRYcIiILMCzgztiaDdv1Gp1ePbLFK6Pcxv+e+wiPt2eDgB4d3RP3OHnIjgRXQsLDhGRBZAkCR88Ho4QDwfkqasx8+vDqNfqRMcyOafyNfjHdw27hD89sANG9eK4G2PFgkNEZCGcba2x9MlI2NsosffcJbybcEp0JJNSWlmLqWtTUFmrxYDQdpg7nOvdGDMWHCIiC9LZ2wnvPdoTALD8jwys289FAJujXqvDzK8PI6ukEv5udvj0id6wUvIt1Jjxd4eIyMI80NMPs2I6AQBe/ek4tp8qFJzIuMmyjFd/TsMfZ4thZ63Esif7wM3BRnQsugkWHCIiC/T8kE54NNIfOhmY/tUhHM9Vi45ktBYmpuPr5CxIEvDvMRHo5nfjXazJOLDgEBFZIEmS8PbDPTAgtB0qa7WYtPoAckurRMcyOuuTs/Dv388AAF5/qDuGdfcRnIiaiwWHiMhC2VgpsGR8JLp4O6GorAaTViVDXVknOpbR+P1EAf654RgAYMY9oXjyziDBiaglWHCIiCyYs601Vk7qCy8nFc4UlCNu5X5oqllyUi5cxoyvD0EnA49F+mPO0M6iI1ELseAQEVm49q52WDu5H9zsrXEkR40JK5NRZsEl53DWZUxclYzqOh3u6eKJtx/pAUmSRMeiFmLBISIihPk448uno+BiZ43DWaWYtOoAKmrqRcdqcykXSvDkimSUVdejX7A7Fo/rDWtOBzdJ/F0jIiIAwB1+Llj3dBScba1w8MJlTFp9AJW1llNyDmSWIG5FMspr6nFniDtWP9UX9jbcY8pUseAQEZFe9/Yu+GJyFJxUVkjOKMHEVQcsYkzOvvOXMGFlMioaVyleNbEfy42JY8EhIqImwgNcsWZyP33JGfvZPhSVme/mnNtPFWLSqgOorNViUCcPrJjQF3Y2StGx6Dax4BAR0VV6B7rh66l3wsPRBicuavDo0r04V1QuOlarW5+chafXHkRVnRZ3d/bE8rg+sLVmuTEHLDhERHRN3du74Ptn+iPA3Q4XLlXikf/sxd5zxaJjtQqtTsa7Cacw98dj0OpkPNK7PcuNmWHBISKi6wr2cMCGZwegV6Ar1FV1iFuRjLVJmZBlWXS0W6aprsOUtQexZMc5AA2L+H34WDhsrPiWaE74u0lERDfk4ajC11PuxMhwP9TrZMz7OQ2zvz1ikjOs0vLUGPXpHmw7VQiVlQIfj4nAP2K7cJ0bM8SCQ0REN2VrrcTCsRF4ZURXKBUSNhzOxchFu01mk05ZlvFFUiYe/s9enC+ugK+LLb57JhqjerUXHY0MRJJN+T7jLdJoNHBxcYFarYazM3eFJSJqiX3nL+G5rw+jsKwG1koJs2I6Y+pdIUa7IN5FdRVe/uEYdp0pAgAMCfPCB4+Fw83BRnAyaqmWvH+z4LDgEBG12OWKWsz98Sg2pxUAALr6OuPd0T3Q099VbLC/0OpkfLX/At7bfBpl1fWwsVLgpdgumDywAz+SMlEsODfBgkNEdPtkWcYPh3LxxqYTUFfVQZKAxyMDMCe2M7ycbIVmS84oweub0nA8VwOgYW2fDx8LR6iXo9BcdHtYcG6CBYeIqPUUl9fgjU0n8HNqHgDAwUaJiQOC8fTAkDb/GOh4rhofbjmN7acbPo5ysrXCi7FdMC4qCEoF79qYupa8fxvsA9O33noL/fv3h729PVxdXZv1HFmWMW/ePPj6+sLOzg4xMTE4e/Zsk3NKSkowbtw4ODs7w9XVFZMnT0Z5ufktPkVEZCo8HFX4ZGwv/DAtGuEBrqio1WLx9nMY+O42vP7LCWQUVxj0++t0MnadKcKTK/bjgUW7sf10EZQKCU/0C8S2OYMRFx3McmOBDHYHZ/78+XB1dUVOTg5WrFiB0tLSmz7n3XffxYIFC7BmzRp06NABr776Ko4dO4YTJ07A1rbhdufw4cNx8eJFfPbZZ6irq8OkSZPQt29ffPXVV83Oxjs4RESGodPJ2HqyAAsTzyItT6N/fGCoBx6M8MOw7j5wtrVule+VXliOX49exHcp2ci5XAUAUEjAAz39MCumE0I8+XGUuTGqj6hWr16NWbNm3bTgyLIMPz8/zJkzB//4xz8AAGq1Gt7e3li9ejXGjh2LkydPolu3bjhw4AD69OkDAEhISMD999+PnJwc+Pn5NSsTCw4RkWHJsoydZ4qwZm8mdpwpwpV3GmulhN6Bbrirsyd6Bbqie3uXZhUeWZaRp65GalYpDmSWYNfZIpwv+vPOkJPKCqMj/TF5YAcEuNsb6mWRYC15/zaarVIzMjKQn5+PmJgY/WMuLi6IiopCUlISxo4di6SkJLi6uurLDQDExMRAoVBg//79ePjhh6957ZqaGtTU/LlRnEajueZ5RETUOiRJwuAuXhjcxQtZlyqx8UgufkrNQ3phOfZnlGB/Ron+XG9nFQLc7OHlrIKTyhq21grU62TU1OtQUlGLwrJqZBRVoKJW2+R7WCslRHf0wKgIPwzv7ssNMqkJoyk4+fn5AABvb+8mj3t7e+u/lp+fDy8vryZft7Kygru7u/6ca1mwYAH+9a9/tXJiIiJqjsB29phxbyfMuLcTMosr8MfZIiSdv4SjOWrkXK5CgaYGBZqb71ZupZDQydsJ/YLd0K9DO9zV2QNOrfRxF5mfFhWcuXPn4t13373hOSdPnkRYWNhthWpt8fHxmD17tv7XGo0GAQEBAhMREVmmYA8HBHs44MnoYABAaWUtLlyqRFZJJUoqalFeU4/qOi2UCgnWSgXaOdjAw1GFoHb2CPZwMNrFBMn4tKjgzJkzBxMnTrzhOSEhIbcUxMfHBwBQUFAAX19f/eMFBQWIiIjQn1NYWNjkefX19SgpKdE//1pUKhVUKtUt5SIiIsNxtbeBq70NwgNcRUchM9OiguPp6QlPT0+DBOnQoQN8fHyQmJioLzQajQb79+/HtGnTAADR0dEoLS1FSkoKIiMjAQDbtm2DTqdDVFSUQXIRERGR6THYvb6srCykpqYiKysLWq0WqampSE1NbbJmTVhYGDZs2ACgYUDarFmz8Oabb2Ljxo04duwY4uLi4Ofnh1GjRgEAunbtimHDhmHKlClITk7Gnj17MGPGDIwdO7bZM6iIiIjI/BlskPG8efOwZs0a/a979eoFANi+fTsGDx4MADh9+jTU6j93on3ppZdQUVGBqVOnorS0FAMHDkRCQoJ+DRwAWLduHWbMmIEhQ4ZAoVBg9OjRWLhwoaFeBhEREZkgbtXAdXCIiIhMglFs1UBEREQkCgsOERERmR0WHCIiIjI7LDhERERkdlhwiIiIyOyw4BAREZHZYcEhIiIis8OCQ0RERGaHBYeIiIjMjsG2ajBmVxZv1mg0gpMQERFRc115327OJgwWWXDKysoAAAEBAYKTEBERUUuVlZXBxcXlhudY5F5UOp0OeXl5cHJygiRJrXptjUaDgIAAZGdnc5+r/8GfzY3x53Nj/PncGH8+18efzY2Z0s9HlmWUlZXBz88PCsWNR9lY5B0chUIBf39/g34PZ2dno/+DIgp/NjfGn8+N8edzY/z5XB9/NjdmKj+fm925uYKDjImIiMjssOAQERGR2WHBaWUqlQrz58+HSqUSHcXo8GdzY/z53Bh/PjfGn8/18WdzY+b687HIQcZERERk3ngHh4iIiMwOCw4RERGZHRYcIiIiMjssOERERGR2WHBa0eLFixEcHAxbW1tERUUhOTlZdCSjsWvXLowcORJ+fn6QJAk//fST6EhGY8GCBejbty+cnJzg5eWFUaNG4fTp06JjGY0lS5agZ8+e+kXIoqOj8dtvv4mOZZTeeecdSJKEWbNmiY5iFF577TVIktTkCAsLEx3LqOTm5mL8+PFo164d7Ozs0KNHDxw8eFB0rFbBgtNKvvnmG8yePRvz58/HoUOHEB4ejtjYWBQWFoqOZhQqKioQHh6OxYsXi45idHbu3Inp06dj37592Lp1K+rq6jB06FBUVFSIjmYU/P398c477yAlJQUHDx7Evffei4ceeghpaWmioxmVAwcO4LPPPkPPnj1FRzEqd9xxBy5evKg/du/eLTqS0bh8+TIGDBgAa2tr/Pbbbzhx4gQ+/PBDuLm5iY7WOmRqFf369ZOnT5+u/7VWq5X9/PzkBQsWCExlnADIGzZsEB3DaBUWFsoA5J07d4qOYrTc3Nzkzz//XHQMo1FWViZ36tRJ3rp1q3z33XfLzz//vOhIRmH+/PlyeHi46BhG6+WXX5YHDhwoOobB8A5OK6itrUVKSgpiYmL0jykUCsTExCApKUlgMjJFarUaAODu7i44ifHRarVYv349KioqEB0dLTqO0Zg+fTpGjBjR5O8ganD27Fn4+fkhJCQE48aNQ1ZWluhIRmPjxo3o06cPHnvsMXh5eaFXr15Yvny56FithgWnFRQXF0Or1cLb27vJ497e3sjPzxeUikyRTqfDrFmzMGDAAHTv3l10HKNx7NgxODo6QqVS4ZlnnsGGDRvQrVs30bGMwvr163Ho0CEsWLBAdBSjExUVhdWrVyMhIQFLlixBRkYGBg0ahLKyMtHRjML58+exZMkSdOrUCZs3b8a0adPw3HPPYc2aNaKjtQqL3E2cyFhNnz4dx48f5ziB/9GlSxekpqZCrVbj+++/x4QJE7Bz506LLznZ2dl4/vnnsXXrVtja2oqOY3SGDx+u//89e/ZEVFQUgoKC8O2332Ly5MkCkxkHnU6HPn364O233wYA9OrVC8ePH8fSpUsxYcIEweluH+/gtAIPDw8olUoUFBQ0ebygoAA+Pj6CUpGpmTFjBjZt2oTt27fD399fdByjYmNjg9DQUERGRmLBggUIDw/HJ598IjqWcCkpKSgsLETv3r1hZWUFKysr7Ny5EwsXLoSVlRW0Wq3oiEbF1dUVnTt3Rnp6uugoRsHX1/eqfyR07drVbD7GY8FpBTY2NoiMjERiYqL+MZ1Oh8TERI4ToJuSZRkzZszAhg0bsG3bNnTo0EF0JKOn0+lQU1MjOoZwQ4YMwbFjx5Camqo/+vTpg3HjxiE1NRVKpVJ0RKNSXl6Oc+fOwdfXV3QUozBgwICrlqQ4c+YMgoKCBCVqXfyIqpXMnj0bEyZMQJ8+fdCvXz98/PHHqKiowKRJk0RHMwrl5eVN/tWUkZGB1NRUuLu7IzAwUGAy8aZPn46vvvoKP//8M5ycnPTjtlxcXGBnZyc4nXjx8fEYPnw4AgMDUVZWhq+++go7duzA5s2bRUcTzsnJ6aqxWg4ODmjXrh3HcAH4xz/+gZEjRyIoKAh5eXmYP38+lEolnnjiCdHRjMILL7yA/v374+2338bjjz+O5ORkLFu2DMuWLRMdrXWInsZlThYtWiQHBgbKNjY2cr9+/eR9+/aJjmQ0tm/fLgO46pgwYYLoaMJd6+cCQF61apXoaEbhqaeekoOCgmQbGxvZ09NTHjJkiLxlyxbRsYwWp4n/acyYMbKvr69sY2Mjt2/fXh4zZoycnp4uOpZR+eWXX+Tu3bvLKpVKDgsLk5ctWyY6UquRZFmWBXUrIiIiIoPgGBwiIiIyOyw4REREZHZYcIiIiMjssOAQERGR2WHBISIiIrPDgkNERERmhwWHiIiIzA4LDhEREZkdFhwiIiIyOyw4REREZHZYcIiIiMjssOAQERGR2fl/dYvO+rD7BaEAAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"x = np.linspace(0, 2*np.pi, num=200) # Definiere einen linearen Bereich von 0 bis 2pi\n",
|
||
"y = np.sin(x) # Berechne den Sinus mit den Werten von x\n",
|
||
"\n",
|
||
"plt.plot(x, y) # Setze für die X-Achse x und für die Y-Achse y\n",
|
||
"plt.show() # Zeige den Plot"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "9dc5f266-8956-431d-aa8e-cb33afc8fc34",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-1dd3b7172bc39b59",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Zwei Funktionen \n",
|
||
"\n",
|
||
"Wie bereits zuvor erwähnt, lässt sich `plt.plot` mehrfach aufrufen. Im Folgenden wollen wir zusätzlich die Kosinus-Funktion mit [np.cos](https://numpy.org/doc/stable/reference/generated/numpy.cos.html) plotten. \n",
|
||
"\n",
|
||
"Dabei werden die Werte aus der bereits definierten x-Skala wiederverwendet. Die Variablen `y1 = np.sin(x)` und `y2 = np.cos(x)` enthalten die jeweiligen y-Werte für Sinus und Kosinus. Auf diese Weise können beide Funktionen in einem gemeinsamen Plot dargestellt werden, was den direkten Vergleich erleichtert.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 30,
|
||
"id": "7f63b65d-875d-4ee2-998b-fc6f39935ab0",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-2e9cc2ce95f1e20e",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAfZJJREFUeJzt3XlclOX6x/HPzLDvILuCu+KOK+KSphyXrLSstCyXTE+lbXZaPL/Kdk/7ama5VpatltnJMvcVFMV9FwRFQERZZZuZ3x8PoJxcABnumeF6v17z4nF4ZuY7aM3F/dz3devMZrMZIYQQQgg7olcdQAghhBCitkmBI4QQQgi7IwWOEEIIIeyOFDhCCCGEsDtS4AghhBDC7kiBI4QQQgi7IwWOEEIIIeyOFDhCCCGEsDsOqgOoYDKZSE1NxdPTE51OpzqOEEIIIarAbDaTm5tLaGgoev3Vx2jqZYGTmppKWFiY6hhCCCGEqIGUlBQaNWp01XPqZYHj6ekJaD8gLy8vxWmEEEIIURU5OTmEhYVVfI5fTb0scMovS3l5eUmBI4QQQtiYqkwvkUnGQgghhLA7UuAIIYQQwu5IgSOEEEIIuyMFjhBCCCHsjhQ4QgghhLA7UuAIIYQQwu5IgSOEEEIIuyMFjhBCCCHsjhQ4QgghhLA7Fi1w1q9fzy233EJoaCg6nY6ff/75mo9Zu3YtXbp0wdnZmRYtWrBw4cK/nTNr1iyaNGmCi4sLUVFRxMXF1X54IYQQQtgsixY4+fn5dOrUiVmzZlXp/MTERIYNG8aNN95IQkICjz/+OA888AB//PFHxTnffvst06ZNY8aMGezYsYNOnToxePBgMjIyLPU2hBBCCGFjdGaz2VwnL6TTsXTpUkaMGHHFc5555hl+++039u7dW3Hf6NGjOX/+PCtWrAAgKiqK7t278/HHHwNgMpkICwvjkUce4dlnn61SlpycHLy9vcnOzpa9qIQQQggbUZ3Pb6vabHPLli3ExMRUum/w4ME8/vjjABQXFxMfH8/06dMrvq/X64mJiWHLli1XfN6ioiKKiooq/pyTk1O7wculxMGeH8DRBRzdwNUPvELBtzH4twIHZ8u8rqiRolIjiZn5JJ7J50xeEZl5xRSVGik1mnE06PF0ccDHzZFGvm409nMj3M8Nvf7aG7wJIUS9YTJC1nHISoSck5CfCSUFUHIBwqKg/e3KollVgZOWlkZQUFCl+4KCgsjJyeHChQucO3cOo9F42XMOHjx4xeedOXMmL730kkUyV5K+F+LmXP57egcIaAONe0HTG6BZP3C+9nbvovbkF5Wy4cgZth7PIi4xi0PpuRhNVR/A9HB2oF2oFz2a+nFDqwAiw3xwNMg8fSFEPVJaDCc2QeJ6SNoIaXug9MIVzi2SAsfSpk+fzrRp0yr+nJOTQ1hYWO2/UHAn6PsvKC2E4nwoyIScVDh7FAqzIX2PdoubAwZnaBEDHUZCxM0yumMhRaVG/tqfwdKdJ1l/JJPiUlOl73s6O9As0INgL2f8PZxxdTTgYNBTYjSRW1jC2bxiUs4VcOJsAXlFpcQmZhGbmMVHq4/i4+bITR1CGBHZkO5NfNHpZHRHCGGHTCZIXAe7v4NDv2mfZ5dycAX/FuDVCDwCwckdHFygUTc1ectjKX31/xEcHEx6enql+9LT0/Hy8sLV1RWDwYDBYLjsOcHBwVd8XmdnZ5yd66CAaNRVu/0vsxmyT0LqDkjcAMdWaUN6h37Tbm7+0PleiHoQvEIsn7MeyMgpZMHmJJbEJXOuoKTi/nA/N/q3DqBHUz+6hPsS4u1SpcKk1Gji2Jl8ElLOseFIJhuPZnK+oISvY5P5OjaZloEejO3VhDu6NMLVyWDJtyaEEHWjKBfiF8G2uXAu8eL97oHQYiA06QthPcCvGeit7/97VlXgREdH89///rfSfStXriQ6OhoAJycnunbtyqpVqyomK5tMJlatWsXUqVPrOm7V6XTgE6bd2g7XCp70fbBvKSQshtzTsOl92PoJRI6Bvk9q54pqS8su5MPVR/hh+0mKjdpoTZCXMyO7NGJ4ZENaBXnUaKTFwaCndbAnrYM9GdU9nFKjiS3Hz7IsIZXf9pzmSEYez/+8lw/+OszkG5pxb8/GuDlZ1X9eQghRNYXZsOUTiP0UCs9r9zl7QYc7of1ICO9plQXN/7LoKqq8vDyOHj0KQOfOnXn33Xe58cYb8fPzIzw8nOnTp3Pq1Cm++OILQFsm3r59e6ZMmcL999/P6tWrefTRR/ntt98YPHgwoC0THzduHHPmzKFHjx68//77fPfddxw8ePBvc3OuxKpWURlL4fAK2PwRpGzV7jM4Q8+HoO80cPFWm89G5BaW8PGaoyzclERR2WWoLuE+TL6hOTFtAnGw4FyZ7Asl/Bh/kvmbEjl5TrsWHejpzFODWzOySyOZmCyEsA3GEtg+H9a9AQVntfsatIBej2jFjZO72nxU7/PbogXO2rVrufHGG/92/7hx41i4cCHjx48nKSmJtWvXVnrME088wf79+2nUqBHPP/8848ePr/T4jz/+mLfeeou0tDQiIyP58MMPiYqKqnIuqypwLnViM6x+VZvABdow4JCZWsUs8zsuy2w28+vu07y6fD8ZudpKuW6NfXlqcGuimjWo0ywlRhNLd57io9VHSMnSCp2Ojbx5/bYOtG8ohaoQwoqd2ALLn4AzB7Q/+7eCG/8NbW61qtEaqylwrJXVFjigXb46/Af8+X/a5GSA5gNh+MfaknNRIT2nkGd/3M2aQ2cAaNzAjeeHtWVgm0ClE36LSo0s3JTEx6uPkltUikGv44E+TXniH61wcbSe/1EIIQRFefDncxC/QPuzWwMY8Bx0HgsG67vMLgXONVh1gVOutAg2fQDr3wZjkXapati70OEO1cmswq+7Uvm/pXvIKSzFyaBn6oAWTL6hmVUVEBm5hbz0635+230agNZBnnxwdyQRwVb6b04IUb8kx8LSyXAuSftzl7EQ8xK4+SmNdTVS4FyDTRQ45TKPwE+TtRVYoK22uultcHRVm0uRwhIjL/26j2/iUgDtEtA7d3aiZZD19hRauT+d6T/tJjOvGCeDnudubsN9PRvLsnIhhBomk7awZfUrYDaBdxiM+ETr0WblpMC5BpsqcECb+LX+bVj/pvaPMag93PUFNGiuOlmdSskqYNIX2zmYlotOB4/c2IJHB7a06ATi2pKZV8QzP+xm1UFtz7QRkaG8fnsHWWklhKhbF87BT/+EI2V7PHYcBTe9ZTMLWqTAuQabK3DKHV8HP06E/DPg4qMVOc36qU5VJzYfzeThr3dwvqAEfw9nPhgdSe8W/qpjVYvZbGbexkRm/n4Qo8lMmxAv5o3rRqhP/RyNE0LUscyj8M0obX6nwVkrbLqMtalFLNX5/Lb+X33FRc36wT83QMNuWm+CL2/TlvTZuW+3JXPf/DjOF5TQqZE3yx/pY3PFDWgbzj7QtxmLH4jC38OJA6dzGD5rE7tSzquOJoSwd8fXwdwBWnHj1QgeWAldx9lUcVNdUuDYGq8QGP8bdLgLzEZtWd/qV7XVV3bGbDbz7srDPPPjHowmMyMiQ/n2n9EEe7uojnZdejZrwM9TetM6yJMzuUWM+mwLa8ouXQkhRK3b8wN8NVJr4NeoB0xeAyGdVKeyOClwbJGjC9z+GfQv21V9/Vvw66Parq52wmgy8++le/lw1REAHh3QgvdGRVrVKqnr0cjXjR8eiqZfqwAKS0xM+mI7P+88pTqWEMLebP1Um9pgKoF2t8G4X7X9ouoBKXBslU4H/Z+Fm98HnR52fAG/TLGLIqfEaGLadwl8E5eMXgev39aBaYNa292qI08XR+aO68aIyFBKTWYe/zaBr2OTVccSQtiLzR/Bime046gHYeR87RfkekIKHFvXbQLcsQB0Btj1jc0XOaVGE498vZNfElJx0Ov48O7O3BMVrjqWxTga9Lx7VyTjezUB4N9L9/DdthS1oYQQtm/zx1oDP4B+z8CQ/4C+fn3kyxpVe9BuhPb1h/u1Iged1vnYitprV4XJZOZf3+9ixb40nAx6Zt/bhYFtqra/mC3T63XMuKUtOh0s2JTEMz/tRq/XcUfXRqqjCSFs0eaPtW74AP2ehRunq82jSP0q5+xZuxFwx/yykZyv4ZepNjWSYzabee6XvfxcNnLzyZj6UdyU0+l0vHBzW8ZGN8Zshqd+2CVzcoQQ1VepuHmm3hY3IAWOfWk3Au6Yd7HIWf6ETayuMpvNvPbbAb6OTUang3dHRRLTtv4UN+V0Oh0v3dqOe6LCMZth2ncJ/LorVXUsIYSt2Da3cnHTv/4WNyAFjv1pd1tZkaOHHYu0DshW7v2/jjB3YyIAb9zekVs71d9NRXU6Ha8Ob8+obmGYzPDEtwlsOpqpOpYQwtod/A3++5R23PdfWnFjZwszqksKHHvU7jatQyXAmldh52K1ea7iy60n+KBsKfiMW9pyV/cwxYnU0+t1zLy9A7d00lZXPfhlPIfSclXHEkJYq5Rt8MNEbSufLuO03cDreXEDUuDYr+4PQJ8ntONfH4Wjq9TmuYx1h8/w4rJ9ADwR04oJvZsqTmQ99Hodb9/ZkR5N/MgtKmXCgjjScwpVxxJCWJuzx7TtF0ovQMtBMOxdKW7KSIFjzwa8oHU8NpXCd2Ph9G7ViSocTs9l6uIdGE1mRnZpxKMDW6iOZHWcHQzMua8rzfzdSc0uZOKibeQXlaqOJYSwFnlntA7FBWchtLPWMsQgi6PLSYFjz/R6GD4Lmt4AxXmw+E7IVr8y52xeEfcv3EZuUSk9mvjx+u3t7a6JX23xdXdi4YQeNHB3Yu+pHKZ+vYNSo0l1LCGEaiWF8M1oOJcIPo3hnu/A2UN1KqsiBY69c3CCUV9BYFvIS9NGckqLlMUpLDEy+ct4Tp67QOMGbnx6X1ecHWyrX09dC2/gxtxx3XB20LPm0Blm/n5QdSQhhEpmM/z2JJzaDq6+cO+P9Wb7heqQAqc+cPGG0V+Di4/2H0T5TPs6Zjab+fdPe4g/cQ4vFwfmjeuOn7uTkiy2pnO4L++PigRg3sZElsnycSHqr+3zIOErbbXsHQvAv6XqRFZJCpz6wq8pjJwH6LTl4/EL6zzCV7HJ/LTzFAa9jtn3dqVFoAynVsfQDiE81L85AM/8sJvD6bKySoh6J3kr/P6sdjxwBjS/UW0eKyYFTn3SMkZbPgjaKM7J7XX20rtSzvPKr/sBeHZIBL1b+NfZa9uTfw1qTZ8W/lwoMfLPL+PJKSxRHUkIUVdyTmvTDEwl0HYE9H5MdSKrJgVOfdP3SWhzCxiL4dv7IC/D4i95vqCYhxfvoNhoYlDbIB7oK8vBa8pQtgFpQx9XEjPzefK7XZhM1t+tWghxnUqL4ftxkJcOAW20BSSyOOOqpMCpb3Q6GDEb/FtDbqq2QacF96wymcxM+24Xp85rk4rfurOTrJi6Tn7uTnwypgtOBj0r96cze90x1ZGEEJa28gVIiQVnbxi9WFZMVYEUOPWRs6f2H4ijOyRtgI3vWeylZq87xuqDGTg56PlkTBe8XR0t9lr1SacwH14e3g6Ad/48xLakLMWJhBAWc/gPiJ2tHd8+Bxo0V5vHRkiBU1/5t7xkO4fXtVbftWzr8bO88+chAF4Z3o52od61/hr12ege4Yzs0giTGR5fkkD2BZmPI4TdyU2Dnx/SjqMehNZD1eaxIVLg1GeR90D7O8BshB8nQmF2rT119oUSpn2bgMkMt3dpyF3dZI8pS3hpeDsaN3Dj1PkLPPfzXsw2sHu8EKKKTCZY+k+tU3FQB4h5SXUimyIFTn2m08HN74JPOJw/AcunaQ2kasGMX/aSml1IuJ8bLw+XTsWW4uHswPujIjHodfy6K5WfdqjvVC2EqCVbPoLja8HBFe6YB44uqhPZFClw6jsXbxg5H3QG2PsD7Prmup9y2a5Ufk5IRa+D90ZF4uEse6NYUudwX56I0Rp9vfDLXpIy8xUnEkJct1PxsOpl7XjofyCgtdo8NkgKHAFh3eHGf2vHv/0Lso7X+KlSz1/guaV7AJg6oCVdG/vWRkJxDQ/1b0GPpn7kFxt57NsESmS/KiFsV3E+/PiAtlFy2+HQZZzqRDZJChyh6fMENOkLJfnwy1Tt2m81mUxmnvxuFzmFpXRq5M0jA2SH8Lpi0Ot4f1QkXi4O7Eo5z0erjqiOJISoqb9e0n7R9GoIt3wg/W5qSAocodEbYPjH2tLxE5sg7rNqP8X8TYlsOX4WV0cD742KxNEg/7zqUqiPK6/d1gGAT9YeY19q7U0aF0LUkaSNEDdHO771I20zTVEjdfIJNGvWLJo0aYKLiwtRUVHExcVd8dz+/fuj0+n+dhs2bFjFOePHj//b94cMGVIXb8W++TaBQWXXfP96Ec5WvYHcsTN5vPmHtiT8+Zvb0ixAmlCpcEunUIa2D6bUZOZf3++WS1VC2JLifPhlinbcZRy0GKg2j42zeIHz7bffMm3aNGbMmMGOHTvo1KkTgwcPJiPj8lsE/PTTT5w+fbritnfvXgwGA3feeWel84YMGVLpvG++uf7JsQLoej80vQFKL1T5UpXJZOaZH3ZTXGrihlYB3N1DloSr9PLw9vi6OXLgdA6frJEux0LYjL9egnNJ4B0Gg15VncbmWbzAeffdd5k0aRITJkygbdu2fPrpp7i5uTF//vzLnu/n50dwcHDFbeXKlbi5uf2twHF2dq50nq+vDOPVCr0ebi27VJW8uUqXqr6KPcH2E+dwdzLw+m2yJFy1AE9nXrxV63L88ZojHEzLUZxICHFNlS5NfQguXmrz2AGLFjjFxcXEx8cTExNz8QX1emJiYtiyZUuVnmPevHmMHj0ad3f3SvevXbuWwMBAWrduzUMPPcTZs2ev+BxFRUXk5ORUuomr8G1c5UtVJ88V8MbvBwF4ZmgEjXzd6iCguJZbO4Xyj7ZBlBjN/Ov7XXKpSghr9r+XppoPUJvHTli0wMnMzMRoNBIUFFTp/qCgINLS0q75+Li4OPbu3csDDzxQ6f4hQ4bwxRdfsGrVKt544w3WrVvH0KFDMRovv2nkzJkz8fb2rriFhckllGu69FLVskcu2wDQbDbzf0v3kl9spFtjX+6NaqwgqLgcnU7HayPa4+3qyN5TOXy2vuZL/4UQFrbqFbk0ZQFWvcxl3rx5dOjQgR49elS6f/To0dx666106NCBESNGsHz5crZt28batWsv+zzTp08nOzu74paSklIH6W1cxaUqN21VVcLiv52ydOcp1h0+g5ODnjfu6IheL5emrEmglwsv3NwWgA/+OsKxM3mKEwkh/iZ158VLU7e8L5emapFFCxx/f38MBgPp6emV7k9PTyc4OPiqj83Pz2fJkiVMnDjxmq/TrFkz/P39OXr06GW/7+zsjJeXV6WbqALfxtD/We34z+ch/+JlwDO5Rby8fD8Aj8e0pLmsmrJKt3dpSL9WARQbTTwve1UJYV1MRvj1cTCbtH0BW8Rc8yGi6ixa4Dg5OdG1a1dWrVpVcZ/JZGLVqlVER0df9bHff/89RUVF3Hvvvdd8nZMnT3L27FlCQkKuO7P4Hz0fhqD2cCELVj5fcfdrv+3nfEEJ7UK9mNS3mcKA4mp0Oh2vDG+Ps4OezcfOsmxXqupIQohycZ/D6QRty5zBr6tOY3csfolq2rRpfP755yxatIgDBw7w0EMPkZ+fz4QJEwAYO3Ys06dP/9vj5s2bx4gRI2jQoEGl+/Py8njqqafYunUrSUlJrFq1iuHDh9OiRQsGDx5s6bdT/xgc4eb3AZ12mSpxA5uPZfJzQio6Hcy8vYM09LNy4Q3cKrpKv7J8P9kFJYoTCSHIPgWrX9GOY14Ez6Crni6qz+KfTKNGjeLtt9/mhRdeIDIykoSEBFasWFEx8Tg5OZnTp09XesyhQ4fYuHHjZS9PGQwGdu/eza233kqrVq2YOHEiXbt2ZcOGDTg7O1v67dRPYd2hm1aQmpc/wSs/JwAwJiqcjo181OUSVTbphmY0D3AnM6+Yt/48qDqOEGLFM1CcB416QJfxqtPYJZ25Hl6Uz8nJwdvbm+zsbJmPU1UXzsPH3SE/g3dK7uBrl9GsfrI/3m6OqpOJKtpy7Cx3f74VnQ6WPtybyDAf1ZGEqJ8OrYBvRoHOAP9cD8HtVSeyGdX5/JZrC6JqXH041/clAKY6/MKr/dykuLEx0c0bcHuXhpjN8H9L91AqvXGEqHvFBfDfp7Tj6ClS3FiQFDiiyqYfbsV6YwecdSUMOfmB6jiiBv59Uxu8XR3Zl5rDF1tOqI4jRP2z8T3ITtZ63pSvUhUWIQWOqJK1hzJYsT+dV4zjMOsd0B3+A478pTqWqCZ/D2eeGRIBwHt/HeZsXpHiRELUI+dOwOYPtePBr4GT+9XPF9dFChxxTUWlRl5ctg+Afr16o4t6UPvGimehtFhhMlETo7qH0S7Ui9zCUt7+87DqOELUH38+B6WFWpf4NreqTmP3pMAR17RwUxJJZwsI9HTm8X+0gn5Pg3sAnD1ysQOnsBkGvY4Zt2ibcS7Zlsy+1GzFiYSoB46vgwPLtInFQ94A2ZTY4qTAEVd1JreIj1ZrHaKfHhKBh7OD1pRq4AzthLVvQG76VZ5BWKMeTf24pVMoZjO8tGy/dDgWwpKMpfD7M9px9wcgqK3aPPWEFDjiqt5deYi8olI6NPTm9s4NL34jcgyEdobiXFj1srqAosamD43AxVFPXFIWv+05fe0HCCFqZvs8OHMAXP3gxr83thWWIQWOuKJ9qdks2aZtTPrCLW0rb6ap18PQt7TjhK/gVLyChOJ6hPq48lA/rcPx678d4EKxUXEiIexQ/llY85p2PPB5cPVVm6cekQJHXJbZbOaV5fsxm+HmjiF0b+L395PCukPH0drx78+AXOawOZNvaEZDH1dSswuZs/6Y6jhC2J81r0FhNgR3gC7jVKepV6TAEZf15/50th7PwslBz7NDI658YsyL4OgOJ7fB/p/rKp6oJa5OBqbfpP39zl57jNTzFxQnEsKOnDkM8Qu14yFvgN6gNE59IwWO+JuiUiOv//cAAJP7NqORr9uVT/YKgd6Pasd/vSjLxm3QsA4h9GjiR1GpiXdXyrJxIWrNXzPAbISIm6FJb9Vp6h0pcMTfLNqcxImyZeEP9W9+7QdETwWPIDiXBNvmWjyfqF06nY5/D2sDwI87TrI/NUdxIiHsQNJGOPRfbVl4zIuq09RLUuCISrILSvi4bFn4vwa3xt3Z4doPcvaAG/9PO17/Jlw4Z8GEwhIiw3wY1jEEsxn+s0J2GxfiuphMWlM/gG4TwL+l2jz1lBQ4opJP1h4lp7CUiGBPRnZpVPUHdr4XAtpoxc2GdywXUFjM04Nb42jQsf7wGTYcOaM6jhC2a++PkLoTnDyhn+w3pYoUOKLCqfMXWLA5CYBnhkRg0Fej06beAINe0Y5j52h7rgib0riBO/f2bAzA6/89iMkkq+KEqLaSwou9wfo8Dh4BSuPUZ1LgiArv/nmY4lITPZv50b91Df6jbBEDTfuBsVia/9moRwe0xNPFgQOnc1i685TqOELYnrg52m7hnqHQ82HVaeo1KXAEAAdO5/DTzpMATB/aBl1N9knR6WDQq4AO9v4gzf9skK+7Ew/315r/vfPnIQpLpPmfEFVWkAXryy7RD3wenK6yAlVYnBQ4AoA3VxzEbNaWDHcK86n5E4V0hE5lzf9kFMcmTejdhFBvF1KzC1mwKUl1HCFsx8b3oCgbgjpAx1Gq09R7UuAIthw7y5pDZ3DQ63hqcOvrf8L+00HvCMfXajvoCpvi4mjgyUHav4PZa4+SfaFEcSIhbEBOKsR9ph0PfEGa+lkBKXDqObPZzH9+15r63RMVThN/9+t/Ut/G2tJI0EZxZAsHmzOic0NaBXmQU1jK5+uPq44jhPVb/xaUFkJYT2j5D9VpBFLg1Ht/7Etn18ls3J0MPDqwFns19P0XOLrBqe1asythUwx6XcUozvxNiZzJLVKcSAgrlnUcdnyhHcfM0OYjCuWkwKnHjCYz7648BMD9fZri7+Fce0/uGQRRD2rHq14Bk0xWtTWD2gbRqZE3BcVGPll7VHUcIazXmtfBVAot/gGNe6lOI8pIgVOPLd+dyuH0PLxcHHigb7Paf4Hej4KLN5w5AHu+r/3nFxal0+l4arC2Eefircmcko04hfi7tL2w5wfteODzarOISqTAqadKjCbeK9tY8Z/9muPt6lj7L+LqC70f147XvC4bcdqg3i0a0LOZH8VGEx/+dUR1HCGsz+pXATO0uw1COqlOIy4hBU499dOOkySdLcDfw4nxvZpY7oWi/gnugXD+BOxYZLnXERahjeJoc3F+2HGS42fyFCcSwookx8Lh37UNNW98TnUa8T+kwKmHikqNfLhKm1PxUP8WVdtQs6ac3KHf09rx+regRC5z2Jqujf0YGBGI0WTmPRnFEeKi1WXb03QeA/4t1GYRfyMFTj20JC6FU+cvEOzlwpiocMu/YJdx4B0Oeemwfb7lX0/UuvIVVb/uSmV/ao7iNEJYgcQNkLQBDE5ww9Oq04jLkAKnnrlQbOTjNdrozSMDW+DiWAfNqByc4IYnteON70NxgeVfU9SqtqFeDOsYAsCHq2QUR9RzZjOsnakddxkLPmFq84jLkgKnnvliSxJncosI83Plzq51+B9l5BjwCYf8DNg+r+5eV9Saxwe2RKeDFfvS2JearTqOEOokrocTm7TRmz7TVKcRVyAFTj1SUFzKZ2VdaR8b2Aonhzr86zc4wg1Paccb34fi/Lp7bVErWgZ5cnPHUEBGcUQ9dunoTdfx4N1QaRxxZVLg1CNfbT3B2fximjRwY0RkaN0H6HQ3+DaBgkzYNrfuX19ct0cHtECn0zpgyyiOqJeOr4XkLWBwltEbK1cnBc6sWbNo0qQJLi4uREVFERcXd8VzFy5ciE6nq3RzcXGpdI7ZbOaFF14gJCQEV1dXYmJiOHJEfqO8moLiUuas00ZvptzYAgeDgtr20lGcTR9AkSw5tjUtgzy5pWwU5wNZUSXqm0tHb7pNAK8QtXnEVVn8U+7bb79l2rRpzJgxgx07dtCpUycGDx5MRkbGFR/j5eXF6dOnK24nTpyo9P0333yTDz/8kE8//ZTY2Fjc3d0ZPHgwhYWFln47Nmvx1mTO5hcT7ufGbZ0VDql2HA2+TaHgLGz7XF0OUWOPDtRGcf7cn87eUzKKI+qRY6shJRYcXKDPE6rTiGuweIHz7rvvMmnSJCZMmEDbtm359NNPcXNzY/78Ky8X1ul0BAcHV9yCgoIqvmc2m3n//fd57rnnGD58OB07duSLL74gNTWVn3/+2dJvxyZdKDYyZ/0xAKYOUDR6U87gAP2e0Y43fQBFueqyiBppEejJrZ3KRnFkLo6oL8xmrSM7QLeJ4BmsNo+4Jot+0hUXFxMfH09MTMzFF9TriYmJYcuWLVd8XF5eHo0bNyYsLIzhw4ezb9++iu8lJiaSlpZW6Tm9vb2Jioq64nMWFRWRk5NT6VafLI49QWZeMWF+rmpHb8p1uBP8msOFcxD3meo0ogYeGdASvQ5WyiiOqC+OrYJT28HBFfo8rjqNqAKLFjiZmZkYjcZKIzAAQUFBpKWlXfYxrVu3Zv78+fzyyy989dVXmEwmevXqxcmTJwEqHled55w5cybe3t4Vt7Cw+tOz4EKxkU/L5t5MvbEFjipHb8oZHC7OxdnyifTFsUEtAj0qRnHel7k4oj5Y/7b2tdv94BGoNouoEiv4tKssOjqasWPHEhkZSb9+/fjpp58ICAhgzpw5NX7O6dOnk52dXXFLSUmpxcTW7eu4ZDLzimjk68rtXRqpjnNRhzvAp7G2okr2qLJJUwdofXH+OpDOwbT6NSoq6pmkTWUrp5yg1yOq04gqsmiB4+/vj8FgID09vdL96enpBAdX7fqlo6MjnTt35uhRrftu+eOq85zOzs54eXlVutUHhSVGPl2nzb2ZYi2jN+UMjheHeTd9CKVFSuOI6msR6MFN7bVVJLPWHFOcRggL2lA2etP5Xlk5ZUMs+onn5ORE165dWbVqVcV9JpOJVatWER0dXaXnMBqN7Nmzh5AQ7R9V06ZNCQ4OrvScOTk5xMbGVvk564vvt6dwJreIhj6ujLSm0ZtykWPAMwRyUyHha9VpRA08fGNzAH7bnUpipjRvFHboVLy2ekpngN6PqU4jqsHiv9JPmzaNzz//nEWLFnHgwAEeeugh8vPzmTBhAgBjx45l+vTpFee//PLL/Pnnnxw/fpwdO3Zw7733cuLECR544AFAW2H1+OOP8+qrr7Js2TL27NnD2LFjCQ0NZcSIEZZ+OzajxGiqmHvzYL9mddu1uKocnKHXo9rxxvfAWKo2j6i2dqHeDIgIxGSG2WuPqo4jRO1b/472teMorVGpsBkOln6BUaNGcebMGV544QXS0tKIjIxkxYoVFZOEk5OT0esvfvieO3eOSZMmkZaWhq+vL127dmXz5s20bdu24pynn36a/Px8Jk+ezPnz5+nTpw8rVqz4W0PA+mxZQiqnzl/A38OZO7tZ8aTqruNgwztw/gTs/QE6jVadSFTTlBtbsPpgBj/tOMVjMa1o6OOqOpIQtSN9Hxz6DdBBX+labGt0ZrPZrDpEXcvJycHb25vs7Gy7nI9jMpn5x3vrOHYmn2eHRvBgv+aqI13dhndg1cvg3woejgW9FY42iau6+7OtbDl+lvG9mvDire1UxxGidvxwP+z9EdrdBncuVJ1GUL3Pb/kksUN/7k/j2Jl8vFwcGBMVrjrOtXWfBC7ekHkYDixTnUbUwNQBLQD4Ji6ZM7kyYVzYgcyjsPcn7bjvk2qziBqRAsfOmM3mihUt43o1wdPFUXGiKnDxgh7/1I43vKN1DBU2pVfzBkSG+VBUamLexkTVcYS4fhvfA8zQaigEd1CdRtSAFDh2ZsORTPacysbV0cCE3k1Vx6m6ng+Bozuk7YYjK1WnEdWk0+mYeqM2ivPV1hNkF5QoTiTEdTifDLuXaMc3/EttFlFjUuDYmVlrtJUsd/cIx8/dSXGaanDzg+73a8fr35JRHBs0sE0gEcGe5BWVsnBzkuo4QtTcpg/AVApN+0GjbqrTiBqSAseObE/KIjYxC0eDjkk32NDoTbnoR8DgDCfjIGmD6jSimnQ6HVPKRnEWbE4kv0iW/QsblJsGO77Ujsu3lBE2SQocO/LJWm3uzcgujQjxtsGlup5B0GWsdrz+LbVZRI3c1CGEZv7unC8oYXHsCdVxhKi+zR+BsQjCoqBJH9VpxHWQAsdO7EvNZvXBDPQ6+Ke1Lwu/mt6Pgd4BEtdDyjbVaUQ1GfQ6Huyv/fv7fEMihSVGxYmEqIaCLNi+QDu+4SnQ6dTmEddFChw7Mbts9GZYx1Ca+rsrTnMdfMKgY1mzv80fqM0iauS2zg1p6OPKmdwivt9efza2FXZg2zwoyddWTbWIUZ1GXCcpcOzA8TN5/LbnNAAP97fh0Zty5bv1Hliu9aIQNsXRoGfyDc0AbRTHaJIJ48IGlFyA2E+1496Py+iNHZACxw7MWXccsxkGRgTSJsQOOjMHRmi9JzDD5g9VpxE1cFe3MHzdHEnOKmDF3jTVcYS4toTFUJAJ3uHQdoTqNKIWSIFj49JzCvlp50ng4s7OdqF8195d30BuutosotpcnQyMjW4CwKfrjlEPd4QRtsRk1CYXA/SaCgaLb9Mo6oAUODZu/qZESoxmujfxpWtjP9Vxak94T2jUA4zFF4eNhU0ZG90YF0c9e05ls+X4WdVxhLiyA8vgXBK4+kLne1WnEbVEChwblltYwtdbkwGYfIMdjd6Adv27fBRn2zwoylWbR1RbAw9n7irbyX7OuuOK0whxBWYzbHxfO+4xGZxseJGGqEQKHBu2JC6F3KJSmge4MzAiUHWc2tf6JmjQEoqyIX6R6jSiBh7o0wy9DtYdPsOB0zmq4wjxd0kb4HQCOLhqBY6wG1Lg2KgSo4n5m7RNDSf1bYZeb4cz/vV66P2odrz1EygtVptHVFt4AzeGdggB4PP1MoojrNCmsnYUne8Fd3+1WUStkgLHRv26K5XT2YUEeDozonND1XEsp+Mo8AiCnFOw90fVaUQN/LNsyfiyXamcOn9BcRohLpG2F47+BTo9RE9RnUbUMilwbJDZbOazst+Gx/dqgoujQXEiC3Jw1nYaB+03LVmNY3M6NvKhV/MGlJrMzN+YqDqOEBeVt6FoOwL8bHD/PnFVUuDYoPVHMjmYloubk4F7oxqrjmN5XSeAkyecOQBHVqpOI2qgvPHfkrhksgtKFKcRAjifDHt+0I7LL4ULuyIFjg36bL22LcPo7uF4uzkqTlMHXH2g23jteJNs32CL+rUKICLYk/xiI1/JJpzCGmydDWYjNO0HoZ1VpxEWIAWOjdl7KptNR89i0Ou4v08T1XHqTtRDoHeEExvh5HbVaUQ16XQ6/tlPG8VZsClJNuEUahVkXVyZWd6OQtgdKXBsTPncm5s7htDI101xmjrk3RA63qUdb3pfaRRRMzd3DCXU24XMvCKW7jylOo6oz8o31QzqAM0HqE4jLEQKHBty8lxBxaaa5XMa6pVeZdfJDyyHs8fUZhHV5mjQc38fbSLn5+uPY5JNOIUKJYUQN0c77v2obKppx6TAsSHzNmo7M/dp4U+7UG/VcepeYAS0HASYtevnwuaM7hGOl4sDxzPzWXlA9hgTCuz5HvLPgFcjaHeb6jTCgqTAsRHZBSV8uy0FqKejN+XKe1UkLNauowub4uHswJie2sq/eRtkybioY2YzbJmlHUf9Ewz1YJFGPSYFjo34KvYEBcVG2oR40bdlPe622bSfdt28pADiF6pOI2pgfK8mOBp0xCVlsSvlvOo4oj45vkZrN+HoDl3Gqk4jLEwKHBtQXGpi0eYkACbf0BRdfb5mrNNdHMWJ+0y2b7BBQV4u3NIxFNAuuwpRZ8pHb7rcp7WfEHZNChwbsHx3Khm5RQR5OTOsQ6jqOOq1HwkewZB7GvYtVZ1G1ED5ZOPf9pwmVbZvEHUh44C2LQM6iHpQdRpRB6TAsXJms7nit9yx0U1wcpC/MhycoMck7XjLR7J9gw1q39Cbns38MJrMFaOTQljU1k+0r21ulm0Z6gn5tLRysYlZ7EvNwcVRz5iocNVxrEe3+8HRDdL2QNIG1WlEDTzQR5ss/3VcMnlFpYrTCLuWdwZ2fasd95RNNesLKXCs3NyylSYjuzTCx81JcRor4uYHkfdox+XX1YVNGRARSFN/d3ILS/l+e4rqOMKebZ8PxiII7QLhPVWnEXVEChwrlpSZz6qDWq+Q8jkL4hJRDwE6OLwCMo+oTiOqSa/XVfy7nr9J6/EkRK0rKYRtn2vH0VOksV89UicFzqxZs2jSpAkuLi5ERUURFxd3xXM///xz+vbti6+vL76+vsTExPzt/PHjx6PT6SrdhgwZYum3UecWbErEbIYbWwfQPMBDdRzr498CWg/VjmUUxyaN7NIQHzdHUrIusHJ/muo4wh5d2tiv7XDVaUQdsniB8+233zJt2jRmzJjBjh076NSpE4MHDyYjI+Oy569du5a7776bNWvWsGXLFsLCwhg0aBCnTlXeu2bIkCGcPn264vbNN99Y+q3UqewLJXwffxKAiX3qcWO/a4meqn3d9Q3kn1WbRVSbm5NDxdyyudL4T9S2So39Jktjv3rG4gXOu+++y6RJk5gwYQJt27bl008/xc3Njfnz51/2/MWLF/Pwww8TGRlJREQEc+fOxWQysWrVqkrnOTs7ExwcXHHz9fW19FupU0vikikoNhIR7EnvFg1Ux7FejXtBSCSUFmrX2YXNGRutNf7bfuIcO5PPqY4j7Emlxn7jVKcRdcyiBU5xcTHx8fHExMRcfEG9npiYGLZs2VKl5ygoKKCkpAQ/P79K969du5bAwEBat27NQw89xNmzV/7tvaioiJycnEo3a1ZqvNjY7/7e9byx37XodBdHceI+g9IitXlEtQV5uXBLJ2n8JyxAGvvVaxYtcDIzMzEajQQFBVW6PygoiLS0ql1vf+aZZwgNDa1UJA0ZMoQvvviCVatW8cYbb7Bu3TqGDh2K0Wi87HPMnDkTb2/viltYWFjN31Qd+H1vGqnZhfh7OHFrpDT2u6Z2I8CrIeRnwJ4fVKcRNTCxbLLx73vTOHmuQHEaYReksV+9Z9WrqP7zn/+wZMkSli5diouLS8X9o0eP5tZbb6VDhw6MGDGC5cuXs23bNtauXXvZ55k+fTrZ2dkVt5QU616SWv5b7Jioxrg4GhSnsQEGR23jPNB+Y5PGfzanXag3vZo3kMZ/ovaUN/aLGCaN/eopixY4/v7+GAwG0tPTK92fnp5OcHDwVR/79ttv85///Ic///yTjh07XvXcZs2a4e/vz9GjRy/7fWdnZ7y8vCrdrFX8iXMkpJzHyaDn3rJdl0UVdBmnXWfP2AeJ61WnETXwQF/tQ2hJXAq5hSWK0wiblp95sbFf+SVsUe9YtMBxcnKia9eulSYIl08Yjo6OvuLj3nzzTV555RVWrFhBt27drvk6J0+e5OzZs4SEhNRKbpXml43eDI8MJcDTWXEaG+LqA5F3a8exnyqNImqmf6tAmgW4k1tUyg9lKwiFqJFt86Sxn7D8Japp06bx+eefs2jRIg4cOMBDDz1Efn4+EyZMAGDs2LFMnz694vw33niD559/nvnz59OkSRPS0tJIS0sjLy8PgLy8PJ566im2bt1KUlISq1atYvjw4bRo0YLBgwdb+u1Y1MlzBfy+9zQAE/vKkGq1lV9nP/Q7ZB1Xm0VUm16vY3yvJgAs2pyESRr/iZqQxn6ijMULnFGjRvH222/zwgsvEBkZSUJCAitWrKiYeJycnMzp06crzp89ezbFxcXccccdhISEVNzefvttAAwGA7t37+bWW2+lVatWTJw4ka5du7JhwwacnW17xGPR5iRMZujdogERwdZ7Gc1q+beEFjGAGWI/U51G1MDILo3wdHEg6WwBaw5dvleWEFdV0divoTT2q+d0ZnP9m5GZk5ODt7c32dnZVjMfJ6+olOjXV5FbVMr88d0YEBF07QeJvzv6F3w1Epw8Ydp+cLGOv19Rda/9tp/PNyTSp4U/Xz0QpTqOsCVmM8zuBRn74R8vQ+/HVCcStaw6n99WvYqqPvl+ewq5RaU0C3Cnf6tA1XFsV/OB4N8KinMh4WvVaUQNjI1ugl4HG49mcjg9V3UcYUsS12vFjTT2E0iBYxWMJjMLNiUBMKF3U/R6uWZcYzrdxSXjsZ+CyaQ2j6i2MD83/tFWG8Es/+9CiCqJnaN9jbxbGvsJKXCswV8H0knOKsDb1ZGRXRqqjmP7Ot0NLt5wLhGO/KE6jaiBCb21SfZLd57kfEGx4jTCJpxLgkP/1Y57TFYaRVgHKXCsQHljv3uiwnFzclCcxg44XTI8vXW22iyiRqKa+tEmxIvCEhPfxFl3Y05hJeI+B8zQfAAEtFadRlgBKXAU25eaTVxiFga9jrHR0tiv1vSYBDo9JK6D9P2q04hq0ul0TOjdBIAvtyRRapRLjeIqivJgx5fasWzLIMpIgaNYeVv6oe2DCfF2VRvGnviEQ8TN2rE0/rNJt3YKpYG7E6nZhfyxL/3aDxD11+5voSgbfJtCi3+oTiOshBQ4CmXlF/NzQipAxW+rohb1fFj7uvtbKMhSm0VUm4ujgTFR4QAs2CS7jIsrMJsvTi6O+ifo5WNNaORfgkLfxCVTXGqiQ0NvuoT7qo5jf8J7QkgnKC2E+AWq04gauLdnYxwNOrafOMeek9mq4whrdHwtZB4CJw+IvEd1GmFFpMBRpMRo4qutJwAY36sJOmknXvt0Ooh6SDuOmwtG2cDR1gR6uTCsg7bHnIziiMuqWBp+j7Z6UogyUuAo8ue+dE5nF+Lv4cTNnWx/k1Cr1f52cA+E3FQ4sEx1GlED5UvGf92dSkZuoeI0wqpkHYfDK7RjWRou/ocUOIos3Fy2NLxHOM4OBsVp7JiDM3SfqB1vlcnGtqhTmA9dwn0oMZpZvDVZdRxhTeLmAmZtDzr/lqrTCCsjBY4Ce09lsy3pHA56HWN6ytJwi+t2Pxic4GQcnIxXnUbUQPkozuLYExSVGhWnEVahKA92ytJwcWVS4CiwsGxp+E0dQgjyclEbpj7wCIT2I7XjWGn8Z4uGtA8m2MuFzLxilu86rTqOsAa7voGiHPBrru1BJ8T/kAKnjmXmFbGsbGn4eFkaXnfKf8PbtxRy5APS1jga9NxX1ghz/qZEzGaz4kRCKZMJ4j7TjmVpuLgC+VdRx5bEJVNsNNGpkTedw3xUx6k/QiMhvBeYSmH7PNVpRA1o89X07EvNYVvSOdVxhErH10DmYXDy1PaeE+IypMCpQyVGE1+WLw3vLUvD61zPslGc7fOhRFbj2BpfdyduL9uMVpaM13PlS8M73wsuXmqzCKslBU4dWrE3jfScIvw9nLmpgywNr3Oth4F3OBSchb0/qE4jamB8L22y8R/70jh5rkBxGqHE2WNw5A9Ap+05J8QVSIFTh8onF4+JkqXhShgcoMcD2nHsp1qLd2FTWgd70rtFA0xm+EqWjNdPcZ9rX1sOggbN1WYRVk0KnDqy++R54k+cw9Ggq9hfRyjQ+T5wcIW0PZC8RXUaUQPlozjfxCVzoViWjNcrRbmw8yvtOOqfarMIqycFTh0pH70Z1iGEQFkaro6bH3QapR3LLuM2aUBEIGF+rmRfKOHnhFOq44i6lPA1FOeCfytoPkB1GmHlpMCpA2dyiyp6d4wva1gmFOpR9pvfgeVwPkVtFlFtBr2OcdFNAFi4KUmWjNcXJtPFycU9Jmt7zQlxFVLg1IFvypaGR4b5EClLw9ULagtN+4HZCNvmqk4jauDObmG4ORk4lJ7LluNnVccRdeHYKsg6Bs5esjRcVIkUOBZWXHpx1/AJ0tjPepQ3/tuxCIplNY6t8XZ1ZGSXRoA2iiPqgfJLyp3vA2cPtVmETZACx8J+33uajNwiAjydGdpeloZbjVaDwacxXDgHe75TnUbUwLheWmfjvw6kk5IlRapdyzwCR/9CWxr+gOo0wkZIgWNh5ZOL741qjJOD/Litht5wcRVG7BxZMm6DWgR60relPyYzFQ00hZ0q35ah1RDwa6Y2i7AZ8olrQQkp59mZfB5Hg457ZGm49YkcA47ukLEfkjaoTiNqoPyy75K4ZAqKS9WGEZZRmK2tngJZGi6qRQocC1pUNnpzS8dQAjyd1YYRf+fqA5FlkxXLV2cIm9K/VSCNG7iRU1jKTztkybhdSvgaivPAvzU06686jbAhUuBYSEZuIct3a7uGj+vVRG0YcWXlS8YP/gbnkpRGEdWnv3TJ+GZZMm53Ll0aHvVPWRouqkUKHAv5OjaZEqOZLuE+dJKl4dYroBU0HwiYL7aAFzbljm6NcHcycDQjj01HZcm4XTm6Es4lgrM3dBqtOo2wMVLgWIC2NFzbJ0ca+9mAiiXjX0JRntosotq8XBy5s1sYAAs3yy7jdqV8aXiX+8DJXW0WYXOkwLGA/+45TWZeEUFezgxtH6w6jriWFjHg1xyKsmH3EtVpRA2MjdaWjK86mMGJs/mK04haceYQHFsNOr3WuViIaqqTAmfWrFk0adIEFxcXoqKiiIuLu+r533//PREREbi4uNChQwf++9//Vvq+2WzmhRdeICQkBFdXV2JiYjhy5Igl30K1LLhkabijQWpIq6fXy5JxG9cswIP+rQMwm+GLLbJk3C6ULw1vfRP4NlabRdgki3/6fvvtt0ybNo0ZM2awY8cOOnXqxODBg8nIyLjs+Zs3b+buu+9m4sSJ7Ny5kxEjRjBixAj27t1bcc6bb77Jhx9+yKeffkpsbCzu7u4MHjyYwsJCS7+da9qZfI5dKedxMui5W5aG245Od4OTJ2QehuNrVKcRNTC+bDL/d9tSyC+SJeM27cJ5SPhGO5al4aKGLF7gvPvuu0yaNIkJEybQtm1bPv30U9zc3Jg/f/5lz//ggw8YMmQITz31FG3atOGVV16hS5cufPzxx4A2evP+++/z3HPPMXz4cDp27MgXX3xBamoqP//8s6XfzjWVN/a7pVMo/h6yNNxmuHhB5zHasSwZt0k3tAygmb87uUWl/LjjpOo44nokLIaSfAhsC036qk4jbJRFC5zi4mLi4+OJiYm5+IJ6PTExMWzZsuWyj9myZUul8wEGDx5ccX5iYiJpaWmVzvH29iYqKuqKz1lUVEROTk6lmyVk5BTy2+6yXcNlabjt6TEZ0MHhP+DsMdVpRDXp9bqKlgwLNydhMsmlRptkMl68PCVLw23S4fRcHvwynljFG+FatMDJzMzEaDQSFBRU6f6goCDS0tIu+5i0tLSrnl/+tTrPOXPmTLy9vStuYWFhNXo/17I4NplSk5lujX3p0MjbIq8hLKhBc2g5CFkybrtGdm2Eh7MDx8/ks+Fopuo4oiaO/Kn1pHLxgQ53qU4jamDh5iRW7EtjgeKNcOvFDNjp06eTnZ1dcUtJSbHI64zs0ogH+jRl8g2yV4rNKr/ev/MrKMpVm0VUm4ezA3d2K99lXJaM26TypeFdx4GTm9osotqyC0pYWtZVfHzZViqqWLTA8ff3x2AwkJ6eXun+9PR0goMvv3w6ODj4queXf63Oczo7O+Pl5VXpZgnhDdx47ua2DGonS8NtVvMB4N8KinMv7n8jbMq46CbodLDm0BkSM2XJuE3JOAjH12pLw7vLruG26LvtKVwoMRIR7ElUUz+lWSxa4Dg5OdG1a1dWrVpVcZ/JZGLVqlVER0df9jHR0dGVzgdYuXJlxflNmzYlODi40jk5OTnExsZe8TmFqDKd7mLPjdg5Wqt4YVOa+LszoHUgcHE/OGEj4som+EcMAx9ZhWprjCYzi7YkAdo8VJ3i+VMWv0Q1bdo0Pv/8cxYtWsSBAwd46KGHyM/PZ8KECQCMHTuW6dOnV5z/2GOPsWLFCt555x0OHjzIiy++yPbt25k6dSoAOp2Oxx9/nFdffZVly5axZ88exo4dS2hoKCNGjLD02xH1Qae7tdbwWcfg2Kprny+sTvnQ+A/xJ8ktLFEbRlTNhXOwq6zRZnl3cWFTVh/M4OS5C/i4OTI8sqHqODhY+gVGjRrFmTNneOGFF0hLSyMyMpIVK1ZUTBJOTk5Gr79YZ/Xq1Yuvv/6a5557jn//+9+0bNmSn3/+mfbt21ec8/TTT5Ofn8/kyZM5f/48ffr0YcWKFbi4uFj67Yj6wNlDaw2/5WPYOhta/kN1IlFNfVr40yLQg6MZefwQf5IJsmWK9dvxJZQUQFB7aNxbdRpRA+VbpYzuHo6rk0FxGtCZ6+H2uzk5OXh7e5OdnW2x+TjCxmUlwoedATNM2aZtyilsypdbT/D8z3tp0sCN1U/2R6+X5cZWy2SEDyPhfDLc+hF0Gas6kaimw+m5DHpvPXodrH/6Rhr5WmaCeHU+v+vFKiohqs2vqdYiHi725BA25fbODfF0cSDpbAHrDp9RHUdczaHfteLG1Rc63Kk6jaiB8vlug9oGW6y4qS4pcIS4kvIl4wlfQ2G22iyi2tydHRhVtsv4AplsbN0qloaPB0dXpVFE9WUXlPBT2dLwcVbU5FYKHCGupOkNENBGaxm/8yvVaUQNjC1bMr7+8BmOZuSpjiMuJ30fJG0AnUGWhtuoS5eG92ymdmn4paTAEeJKdLqLozhxn2nzBIRNCW/gxsAIbUHDF2XLV4WVKR+9aXMLeDdSm0VUm9Fk5outSYB1LA2/lBQ4QlxNx1Fay/hzSVoLeWFz7r9kyXiOLBm3LgVZsPs77ViWhtuk1QczSMm6gLerdSwNv5QUOEJcjZOb1jIetCXjwuZEN29AqyAPCoqNfL9ddhm3KjsWQWkhBHeE8J6q04gaKJ9cPLpHmFUsDb+UFDhCXEv3B7TW8YnrIOOA6jSimnQ6HeN7aX1wFm1Owii7jFsHYynEzdWOez4ku4bboCPpuWw8moleB/f1bKw6zt9IgSPEtfiEQ8TN2nHsHLVZRI2M6ByKt6sjyVkFrDmYoTqOADi4HHJOgps/tLtddRpRAwvLRm/+0TbIapaGX0oKHCGqonx+wK4lWkt5YVPcnBwY3V1bMr5Qloxbh/JfFrpNAEfpQm9rsi9cXBpePkJqbaTAEaIqGveCoA5QegF2fKE6jaiBe3s2Rq+DjUczOZKeqzpO/XZ6FyRvBr0DdJuoOo2oge/Lloa3DrKupeGXkgJHiKqotGT8c23+gLApYX5u/KOttmRcRnEUKx+9aTsCvEKURhHVV2nX8N7WtTT8UlLgCFFVHe4EtwaQnQKHf1edRtRA+VD6TztOkV0gS8aVyDsDe77XjmVpuE1ac8nS8BFWtjT8UlLgCFFVji5aK3mArZ8qjSJqpmczPyKCPblQYuS77Smq49RPOxaCsRhCu0CjbqrTiBooHwEd3d36loZfSgocIaqj20StpfyJjZC2R3UaUU06nY4JZY3/Fm2RJeN1zlgC2+Zpx1EPytJwG3Tp0vB7rXBp+KWkwBGiOrwbQtvh2rEsGbdJwyMb4uPmyMlzF/jrQLrqOPXL/l8g9zR4BEG721SnETVw6dLwMD/rWxp+KSlwhKiu8nkDe76H/LNqs4hqc3E0cHePcAAWbkpSG6a+qVgafj84OKnNIqrtfEGxVe4afiVS4AhRXWE9ICRSazG/Y6HqNKIG7u3ZGINex5bjZzmYlqM6Tv1wKh5OxoHeEbpOUJ1G1MCSbRd3DY9u1kB1nGuSAkeI6tLpLo7ibJunzSsQNqWhjyuD22lLxhfJkvG6EfuZ9rX97eAZpDaLqLZSo4kvyv5bub9PU6tdGn4pKXCEqIn2t4N7AOSc0lrOC5tTvmR86c5TnMsvVpzGzuWmw94ftePyflLCpvy5P53U7EIauDtxa6dQ1XGqRAocIWrCwVmbRwCyZNxGdW/iS9sQLwpLTHwrS8YtK34BmEqgUQ9o2FV1GlED8zcmAnBPVDgujta7NPxSUuAIUVPd7tdazadshdSdqtOIarp0yfgXm5MoNZrUBrJXpcWXLA2X0RtbtPvkebafOIejQWf1S8MvJQWOEDXlGXxxqWv5/AJhU27pFIqfuxOp2YWs3C9Lxi1i/8+QnwGeIRdbLAibsqBsteGwDiEEednOxqhS4AhxPaIe0r7u/QHyMtRmEdXm4mjgnrIl4wtksnHtM5th62ztuNtEMDiqzSOqLSOnkOW7UwFtcrEtkQJHiOvRqCs07Ka1no9fqDqNqIHyJeNxiVnsS81WHce+nNwOqTvA4AzdZGm4LfoqNpkSo5mujX3p2MhHdZxqkQJHiOt16ZLxUlmNY2uCvV0Y2j4YkCXjtS62bAJ+hzvA3V9tFlFthSVGFm89AcD9vW1r9AakwBHi+rUdDh7BkJcGB5apTiNqoHyy8c8JqWTJkvHakXNam38D0GOy0iiiZn7dlcrZ/GJCvV0q+kbZEilwhLheDk7QfaJ2XD7fQNiULuG+dGjoTXGpiW/iklXHsQ/b5oKpFMKjITRSdRpRTWazmfllk4vvi26Cg8H2ygXbSyyENeo6HgxOcGq7Nu9A2BSdTsf4sr11vtp6ghJZMn59igtge9nS8J4Pqc0iaiQ2MYsDp3NwcdRzd48w1XFqRAocIWqDRyC0H6kdyy7jNunmTiH4ezhxOruQP/alqY5j23YvgQvnwKcxRNysOo2ogQWbtMZ+t3dphI+bbW6MKgWOELWlvInZvqWQKx+QtsbZwcA9UVoTM9ll/DqYTBcv1UY9CHrb6HorLkrJKuDPsr5QE2xg1/ArkQJHiNoS2hnCemot6bfPV51G1MC9UeE46HVsP3GOPSdlyXiNHFsFmYfByRM636s6jaiBRZuTMJuhb0t/WgZ5qo5TYxYtcLKyshgzZgxeXl74+PgwceJE8vLyrnr+I488QuvWrXF1dSU8PJxHH32U7OzK/6PR6XR/uy1ZssSSb0WIqikfxdk+H0qL1GYR1Rbo5cKwjiEALJQl4zWz5WPta5ex4OKlNouotryiUr7dpu3NZotLwy9l0QJnzJgx7Nu3j5UrV7J8+XLWr1/P5MlXXi6YmppKamoqb7/9Nnv37mXhwoWsWLGCiRMn/u3cBQsWcPr06YrbiBEjLPhOhKiiNreAV0PIP6NdqhI2p3yy8a+7UjmTK0VqtaTvg+NrQaeXfads1I/xJ8ktKqWZvzv9WgWojnNdLFbgHDhwgBUrVjB37lyioqLo06cPH330EUuWLCE1NfWyj2nfvj0//vgjt9xyC82bN2fAgAG89tpr/Prrr5SWllY618fHh+Dg4Iqbi4vt7I8h7JjBsfKScbNZbR5RbZ3DfYkM86HYaOKrsiZnooq2fqJ9bXML+NrOpoxCYzKZK0Yux/dugl6vUxvoOlmswNmyZQs+Pj5069at4r6YmBj0ej2xsbFVfp7s7Gy8vLxwcHCodP+UKVPw9/enR48ezJ8/H/NVPkiKiorIycmpdBPCYrqM11rTn06AlDjVaUQNPNBXG5r/ausJCkuMitPYiLwM2P29dtxzitosokbWHs4gMTMfTxcHRnZppDrOdbNYgZOWlkZgYGCl+xwcHPDz8yMtrWorTDIzM3nllVf+dlnr5Zdf5rvvvmPlypWMHDmShx9+mI8++uiKzzNz5ky8vb0rbmFhtrmmX9gI9wbQ8U7tuLxVvbApQ9oF09DHlbP5xfy885TqOLZh2zwwFkHDrhDWQ3UaUQPzNmpLw0d3D8Pd2eEaZ1u/ahc4zz777GUn+V56O3jw4HUHy8nJYdiwYbRt25YXX3yx0veef/55evfuTefOnXnmmWd4+umneeutt674XNOnTyc7O7vilpKSct35hLiq8v2p9v8C2SfVZhHV5mDQV2zfMHdj4lVHiAVQUqh1Lgbo+TDobPvSRn20PzWHTUfPYtDrGGfDS8MvVe0C58knn+TAgQNXvTVr1ozg4GAyMjIqPba0tJSsrCyCg4Ov+hq5ubkMGTIET09Pli5diqOj41XPj4qK4uTJkxQVXX5CoLOzM15eXpVuQlhUcAdo0hfMRmn8Z6Pu6h6Gh7MDRzPyWHf4jOo41m3P91CQqU2wbztcdRpRA3M3HgdgaPtgGvm6KU5TO6o9BhUQEEBAwLVnVkdHR3P+/Hni4+Pp2rUrAKtXr8ZkMhEVFXXFx+Xk5DB48GCcnZ1ZtmxZlSYPJyQk4Ovri7Ozc9XfiBCWFj0VkjZA/CLo9zQ4224/ifrIy8WRUd3DmLcxkXkbE+nfOvDaD6qPzOZLGvv9U5toL2xKek4hv+7SFv880LeZ4jS1x2JzcNq0acOQIUOYNGkScXFxbNq0ialTpzJ69GhCQ0MBOHXqFBEREcTFaRMxc3JyGDRoEPn5+cybN4+cnBzS0tJIS0vDaNQm+v3666/MnTuXvXv3cvToUWbPns3rr7/OI488Yqm3IkTNtBwEDVpCUTbs+FJ1GlED43s1Qa+DDUcyOZgmixMu6/hayNgHju7QZZzqNKIGFm1OosRopnsTbQWhvbBoH5zFixcTERHBwIEDuemmm+jTpw+fffZZxfdLSko4dOgQBQUFAOzYsYPY2Fj27NlDixYtCAkJqbiVz5txdHRk1qxZREdHExkZyZw5c3j33XeZMWOGJd+KENWn10N02WqSrbPBWHr184XVCfNzY2h7rfHfvA2JitNYqS2ztK+dx4Crj9IoovoKiktZHJsM2NfoDYDOXA9nz+Xk5ODt7V2xBF0Iiym5AO+1g4KzcMcCaH+76kSimnYkn+P2TzbjZNCz8dkbCfSUnlsVzhyCWT0AHTwSDw2aq04kqumLLUm88Ms+GjdwY/WT/TFYee+b6nx+y15UQliSoyt0f0A73vKxNP6zQV3CfekSXtb4b4s0/qukfO5N65ukuLFBRpOZ+WVLwyf2aWr1xU11SYEjhKV1n6Q1/jsVDylVb3IprEf50P2X0vjvovyzsKtsD8Doh9VmETXy14F0ks4W4O3qyB1dbb+x3/+SAkcIS/MIgE6jtOPNV25IKazXoLZBNPJ15VxBCT/tkMZ/AMTPh9ILENwRGvdWnUbUQPm8sjFR4bg52X5jv/8lBY4QdSF6qvb14G9w9pjaLKLatMZ/2vYN8zYex2Sq55caS4shrqyxX/QUaexng3alnCcuKQtHg/009vtfUuAIURcCWmvLxrmkZ4iwKXd1a4SnswPHzuRL4799P0FeGngEQzuZOG+LPt+gNfa7pVMoQV72OXFeChwh6kr5kvGExVCQpTaLqDZPF0dG99D2sSv/cKiXzGbY9KF23GMSODipzSOq7eS5An7fq+0J+UAf+1oafikpcISoK037QVAHKCmA+AWq04gaGNerCQa9js3HzrL3VLbqOGocXXWxsV/3iarTiBpYuCkJo8lM7xYNaBtqv61SpMARoq7odNCrbC5O7GfaPAZhUxr5unFzR63x32fr6+kozuYPtK9dx4Grr9osotpyC0tYsk1rnGtvjf3+lxQ4QtSldreDZ4g2f2HvD6rTiBqYfIP2ofDbntOkZBUoTlPHUndC4nrQGbRdw4XNWRKXQl5RKS0CPejX8tr7StoyKXCEqEsOTtqGhACbpfGfLWoX6k3flv4YTWbmbaxn2zeUz71pPxJ8wtRmEdVWXGqq+Dc7qW9T9HbW2O9/SYEjRF3rOh6cPLR5DEf/Up1G1MA/b9C69n67LYVz+fXkUuO5JNj/s3bc+1GVSUQN/ZJwirScQgI9nRnRuaHqOBYnBY4Qdc3VVytyADZ9oDSKqJneLRrQLtSLCyVGvtxaT7Zv2DILzCZoPgCCO6hOI6rJZDJXzBu7v09TnB0MihNZnhQ4QqjQ82HQO0LSBjgZrzqNqCadTlcxF2fh5iT7376hIAt2fqUd95LRG1u0+mAGRzLy8HR24J6ocNVx6oQUOEKo4N0QOt6lHW96T20WUSPDOoTQ0MeVrPxivo8/qTqOZW2bq7U3CO4IzfqrTiNqYM56rYP6PT3D8XJxVJymbkiBI4QqvR/Tvh5YDplH1GYR1eZg0DOpr7Z9w9wNxzHa6/YNJRcgdo523Psx2ZbBBsWfyGJb0jmcDHruL9typD6QAkcIVQJaQ+ubADNs/lB1GlEDd3UPw8fNkRNnC/hjX5rqOJaR8DUUZIJ3OLQdoTqNqIFP12lzb27r3NBut2W4HClwhFCpfBRn1xLItdMPSDvm5uTA2J6NAZiz7hhme1v2bzLClo+14+gpYLC/Haft3dGMXFbuT0eng8n97Lux3/+SAkcIlcJ7QlhPMBbD1k9UpxE1MLZXE5wd9Ow6mc3W43a2x9jB5ZB1HFx8oPO9qtOIGihfOfWPNkE0D/BQnKZuSYEjhGp9Hte+bl8AhfV0fyMb5u/hzJ3dGgHwWdlETrtgNl9sY9D9AXCuXx+O9iAtu5ClO08B8GD/5orT1D0pcIRQreVgCIiAohytyBE254E+zdDpYM2hMxxMy1Edp3ac2ASn4sHgfLH7trApCzYlUmI006OJH13C69++YVLgCKGaXn9xLs7W2VBapDaPqLYm/u4MbR8MwGfr7GQTzg3vaF8j7wGPQLVZRLVlXyhhcWwyAA/2r19zb8pJgSOENWh/B3g11Dbh3LVEdRpRA+XbN/yyK9X2N+E8FQ/HVmubapZfQhU2ZXHsCfKKSmkd5MmNretngSoFjhDWwMFJW6UC2pJxk513xrVDncJ8Kjbh/HSdjc/F2fCu9rXDneDbRGkUUX2FJUYWbEoCYPINzdDV095FUuAIYS26jNNWq5w9Cgd/U51G1MCUG1sA8P32k6TnFCpOU0MZB7XVUwB9nlCbRdTID/EnOZNbRIi3C7dGhqqOo4wUOEJYC2cP6DFJO974rraKRdiUqKZ+dGvsS7HRxOfrbXQuzsay0Zs2t0BghNosotpKjCZmr9VGEP95QzMcDfX3Y77+vnMhrFHUg+DoBqk74dgq1WlENel0OqYM0EZxFscmcy6/WHGiaspKhD0/aMd9n1SbRdTILwmpnDp/AX8PJ0b3qB+bal6JFDhCWBN3f+h2v3a87i0ZxbFB/VsF0L6hFxdKjCzYlKg6TvVs+gDMRmg+EEI7q04jqsloMvPJmqMATOrbDBdHg+JEakmBI4S16fWI1nskZSskbVSdRlSTTqdjSn9tFGfh5iRyC0sUJ6qinNOQsFg7ltEbm/TfPac5npmPj5sjY8q2EKnPpMARwtp4BkOXsdrx+jfVZhE1MrhdMC0CPcgpLOXLrSdUx6maLR9rW4aER0OT3qrTiGoymcx8vFobvbm/d1M8nGXfMClwhLBGvR8DvSMkrofkWNVpRDXp9ToeLmuNP29DIheKrXzZf0EWbJ+vHcvojU3660A6h9Jz8XR2YFyvJqrjWAUpcISwRj5hEHm3drz+LbVZRI3c2imUMD9XzuYXs2Rbsuo4V7d1NpQUQHBHaBGjOo2oJrPZzMdlc2/G9mqMt6uj4kTWwaIFTlZWFmPGjMHLywsfHx8mTpxIXl7eVR/Tv39/dDpdpduDDz5Y6Zzk5GSGDRuGm5sbgYGBPPXUU5SWllryrQhR9/o8oXWSPboSTu1QnUZUk4NBz4P9tFGcz9Yfp7jUpDjRFRTmQNwc7bjvk1BPm8LZsvVHMtl9MhtXRwP3926qOo7VsGiBM2bMGPbt28fKlStZvnw569evZ/Lkydd83KRJkzh9+nTF7c03L85DMBqNDBs2jOLiYjZv3syiRYtYuHAhL7zwgiXfihB1z6+Z1kkWLu4LJGzKHV0bEeTlzOnsQn7acVJ1nMvbPk/bxb5BS633jbApZrOZj1YdAeCeqHAaeDgrTmQ9LFbgHDhwgBUrVjB37lyioqLo06cPH330EUuWLCE1NfWqj3VzcyM4OLji5uXlVfG9P//8k/379/PVV18RGRnJ0KFDeeWVV5g1axbFxTbWc0KIa+n7JKDTOsum7VWdRlSTs4OBSX21jQ5nrztGqdHKRnGKC2DLLO247zTQ1+9lxbYoNjGL7SfO4WTQM/mG+rmp5pVYrMDZsmULPj4+dOvWreK+mJgY9Ho9sbFXnzS5ePFi/P39ad++PdOnT6eg4OLGdVu2bKFDhw4EBQVV3Dd48GBycnLYt2/fZZ+vqKiInJycSjchbEJAK2g3QjuWURybdE9UOH7uTpw4W8Bve06rjlNZ/ALIPwPe4RdHC4VNKV85dVf3RgR5uShOY10sVuCkpaURGFh5B1MHBwf8/PxIS0u74uPuuecevvrqK9asWcP06dP58ssvuffeeys976XFDVDx5ys978yZM/H29q64hYWF1fRtCVH3+v5L+7pvKZw5rDaLqDY3Jwcm9tHmRXy46ghGk5U0bywugI3va8c3/AsMMjHV1uxIPsfGo5k46HUVu9mLi6pd4Dz77LN/mwT8v7eDBw/WONDkyZMZPHgwHTp0YMyYMXzxxRcsXbqUY8dqvjvv9OnTyc7OrrilpKTU+LmEqHPB7aH1MMB8cZ8gYVPGRjfGx82RY2fyWb776pfo60z8AsjPAJ9w6HS36jSiBmaVjd7c1rkhYX5uitNYn2oXOE8++SQHDhy46q1Zs2YEBweTkZFR6bGlpaVkZWURHBxc5deLiooC4OhR7S8yODiY9PT0SueU//lKz+vs7IyXl1elmxA25Yay3iS7v9P2CxI2xdPFsWIuzgfWMIpTckHblgG0EUIHJ7V5RLXtOZnNqoMZ6HXwUH8Zvbmcahc4AQEBREREXPXm5OREdHQ058+fJz4+vuKxq1evxmQyVRQtVZGQkABASEgIANHR0ezZs6dS8bRy5Uq8vLxo27Ztdd+OELahYVdtfyCzETa8rTqNqIHyUZzjZ/L5dZfiUZztCyAvXUZvbNh7f2mXq4dHNqRZgIfiNNbJYnNw2rRpw5AhQ5g0aRJxcXFs2rSJqVOnMnr0aEJDQwE4deoUERERxMXFAXDs2DFeeeUV4uPjSUpKYtmyZYwdO5YbbriBjh07AjBo0CDatm3Lfffdx65du/jjjz947rnnmDJlCs7OsjxO2LH+z2pfE76BszW/ZCvUuHQUR+lcnJILsOl97VhGb2zSzuRzrD6YgUGv49GBLVXHsVoW7YOzePFiIiIiGDhwIDfddBN9+vThs88+q/h+SUkJhw4dqlgl5eTkxF9//cWgQYOIiIjgySefZOTIkfz6668VjzEYDCxfvhyDwUB0dDT33nsvY8eO5eWXX7bkWxFCvbAe0OIf2iiOdDe2SeN6NcHXzZHjmfks23VKTQgZvbF57/2l9b25rXNDmvq7K05jvXRms9lKpvTXnZycHLy9vcnOzpb5OMK2nNoBn98IOj08HKstIxc25ZO1R3lzxSGa+bvz5xM34GCowx1zSi7AB520AueWD6HruLp7bVEr4k9kMXL2Fgx6HWue7E94g/o1ubg6n9+yF5UQtqRhF2h9E5hNsO4N1WlEDYyNvnQUp47n4sjojc17b6U2enNHl0b1rripLilwhLA1/adrX/f+COn71WYR1ebh7MDksp4lH60+WnfdjYvyLjaLlLk3Nin2+NmKvjdTB7RQHcfqSYEjhK0J6QhtbgXMsO4/qtOIGhgb3Rg/dycSM/P5aUcdzcWJ/RQKMsG3KUTeUzevKWpV+cqpu7qHSd+bKpACRwhb1H86oIP9v0DaHtVpRDW5OzvwcFnvkvf/OkxRqdGyL3jhHGz+UDu+8f+ka7EN2nwsk63Hs3Ay6Jlyo4zeVIUUOELYoqC20P527XjNTLVZRI3c27MxId4upGYX8nVssmVfbPNH2o7hgW2h/UjLvpaodWazmbf/OATAqO5hNPRxVZzINkiBI4St6vestprq0G9wMv7a5wur4uJoqOhhMmvNUfKLSi3zQnlnYOun2vGN/wd6+d++rVl1IIMdyedxcdTL3JtqkH/pQtiqgFYXV8L8NQPqX8cHm3dH10Y0aeBGZl4xCzcnWeZFNr4LJfkQ2gUihlnmNYTFGE1m3iobvZnQu6nsGF4NUuAIYcv6PwsGJ0jaAMdWq04jqsnRoOeJf2i9jD5dd4zsgpLafYHsk7BtrnY84DnQ6Wr3+YXFLdt1ikPpuXi5OPCg7BheLVLgCGHLfMKh+yTteNVLYKqjJcei1tzSMZSIYE9yC0uZs76Wt+BY9yYYi6FxH2g+oHafW1hccamJd1dqK6ce7N8cbzeZHF4dUuAIYev6TgMnTzi9C/YvVZ1GVJNer+PJQa0BWLApiYzcwtp54syjsPMr7Xjg8zJ6Y4OWbEsmJesCAZ7OTOjVVHUcmyMFjhC2zt0fej2iHa9+FYy1fJlDWFxMm0Aiw3y4UGLko1VHa+dJV72k7VvWcjCE96yd5xR1pqC4lA/L/i08OrAlrk4GxYlsjxQ4QtiD6Cng5g9Zx2Hnl6rTiGrS6XQ8MyQCgG/ikjl+Ju/6njAlDg4s01bZxbx4/QFFnVuwKYnMvCLC/dwY1S1MdRybJAWOEPbA2QP6Pa0dr30DigvU5hHVFt28AQMiAik1mXlzxaGaP5HZDH8+rx1H3qP1TBI25Vx+MZ+u0+ZjPTmoFU4O8lFdE/JTE8JedJ2gTTrOS4PY2arTiBp4dmgEeh2s2JfG9qSsmj3Jof9CylZwcIX+/67dgKJOfLj6CLmFpbQJ8eKWjqGq49gsKXCEsBcOTjCg7Df3De9pDd6ETWkV5MldZZcjXv/vAczV7W1kLIW/XtSOox8G74a1G1BYXGJmPl9uOQHAc8PaoNfL5PCakgJHCHvS/g4I7QzFubD2ddVpRA088Y9WuDoa2JF8nhV706r34J1fQuZhcPWD3o9ZJqCwqDd+P0ipycyNrQPo3cJfdRybJgWOEPZEr4dBr2nH8Qsh44DSOKL6grxcmNRXWxL8xoqDlBir2NuoOB/Wlu1L1u8ZcPG2UEJhKXGJWazYl4ZeB/++qY3qODZPChwh7E2T3hBxM5hNFyebCpsyuV9z/D2cSDpbUPWNODd/DHnp4NsEut1v0Xyi9plMZl77bT8Ao3uE0zLIU3Ei2ycFjhD26B8vg94Bjq6ULRxskIezA4/FaFs4fLDqCDmF1+htlH0KNr2vHQ+coc3HEjZl+Z7T7DqZjbuTgSfK/u7F9ZECRwh71KA59JisHf/xHJiMavOIahvdPYzmAe5k5Rfz0aojVz/5rxehpADCo6HdbXWST9SewhIjb/x+EICH+jcnwNNZcSL7IAWOEPbqhqfAxQcy9kHCYtVpRDU5GvQ8f7PWw2bBpiSOXan5X0oc7PkO0MGQmbIlgw1auDmJU+cvEOzlwsQ+zVTHsRtS4Ahhr9z8Ljb/W/0qFOWqzSOqrX/rwIrmf68u3//3E0wm+P0Z7bjzGG0FnbAp6TmFFSN0Tw1uLVsy1CIpcISwZ90ngV8zbfLpujdVpxE18NywNjgadKw5dIY1BzMqf3P3t5C6Q9tsdcALagKK6/LG7wfJLzbSOdyH2zpL36LaJAWOEPbMwQmGvKEdb/0EzhxWm0dUW7MADyb01paNv/LbfopLy5aNF+VdbOp3w5PgGaQmoKix+BNZ/LTzFDodvHhLO2nqV8ukwBHC3rUaBK2GgqkUfn9K26tI2JRHBrTA38OJ42fy+WJLknbnxve0bTl8m0DPh1XGEzVgNJmZsWwfAHd1DaNTmI/aQHZIChwh6oMhr4PBGY6vhQO/qk4jqsnTxZGnB2u7jX/w1xGyTh6CzR9p3xz0GjjIqhtb8+22FPaeysHTxYGnhrRWHccuSYEjRH3g1wx6P6od//F/stu4DbqjayM6NPQmt6iE9CWPgrEImvaDiGGqo4lqyi4o4a0/tGXhT8S0wt9DClRLkAJHiPqizzTwDoPs5ItN4YTN0Ot1vHhrOwbrt9EmbysmvSMMe0eWhdugd1ce4lxBCa2CPLgvurHqOHZLChwh6gsnNxhctk/VxvchK1FpHFF9XYMdecP9awCWON5GiW9zxYlEde1LzebLrdpu4S/e0g5Hg3wMW4r8ZIWoT9rcql3WMBbB70/LhGNbs+4/+JRkcJJAXsq+ifkbpUi1JUaTmek/7cFkhmEdQ+glu4VblBQ4QtQnOh3c9DYYnODIn7BvqepEoqrS98GWTwBI6vEiRTjx/l9HOHlO5lPZii+3JLH7ZDaeLg7MKOtSLSzHogVOVlYWY8aMwcvLCx8fHyZOnEhe3hXajQNJSUnodLrL3r7//vuK8y73/SVLlljyrQhhPwJaQd8ntePfn4EL59TmEddmMsHyaWA2QsTN9B56D1FN/bhQYuTFZZfpcCyszunsC7z1xyEAnhkSQaCXi+JE9s+iBc6YMWPYt28fK1euZPny5axfv57Jkydf8fywsDBOnz5d6fbSSy/h4eHB0KFDK527YMGCSueNGDHCkm9FCPvS5wnwbwX5GbByhuo04lp2fQ0pW8HRDYb8B51Ox2u3tcfRoOOvA+n8uS9NdUJxDS8u20d+sZEu4T7c0yNcdZx6wWIFzoEDB1ixYgVz584lKiqKPn368NFHH7FkyRJSU1Mv+xiDwUBwcHCl29KlS7nrrrvw8PCodK6Pj0+l81xcpBoWosocnOHm97XjHYvgxGalccRV5KZrS/sB+j8LPmEAtAj0ZFJfbWPGF5ftI7+oVFVCcQ1/7kvjj33pOOh1vH57B+lYXEcsVuBs2bIFHx8funXrVnFfTEwMer2e2NjYKj1HfHw8CQkJTJw48W/fmzJlCv7+/vTo0YP58+djvspkyaKiInJycirdhKj3mvSGLuO0418fg9IitXnE35nN8Ns0KDwPIZ3+1rH4kQEtCfNzJTW7kDdWHFSTUVxVXlFpRcfiSTc0IyLYS3Gi+sNiBU5aWhqBgYGV7nNwcMDPz4+0tKoNp86bN482bdrQq1evSve//PLLfPfdd6xcuZKRI0fy8MMP89FHH13xeWbOnIm3t3fFLSwsrPpvSAh79I+XwD0QMg9rrf+Fddn/MxxcDnoHGD4LDI6Vvu3qZOA/t3cE4IstJ9hy7KyCkOJq3v7jEKezCwn3c+PRAS1Vx6lXql3gPPvss1ecCFx+O3jw+n+TuHDhAl9//fVlR2+ef/55evfuTefOnXnmmWd4+umneeutt674XNOnTyc7O7vilpKSct35hLALrr4wtGwzzg3vQLpMWLUa+Wfhv09px32mQXCHy57Wu4U/d5fN6Xjmx90UFMulKmux9fhZFm5OAuDVEe1xdTKoDVTPVLvAefLJJzlw4MBVb82aNSM4OJiMjIxKjy0tLSUrK4vg4OBrvs4PP/xAQUEBY8eOvea5UVFRnDx5kqKiyw+xOzs74+XlVekmhCjT7jZtM05jMSz9JxhLVCcSACuehfwzENAGbvjXVU/9900RhHq7kJxVULFSR6iVX1TKUz/sAuDuHmHc0CpAcaL6x6G6DwgICCAg4Np/UdHR0Zw/f574+Hi6du0KwOrVqzGZTERFRV3z8fPmzePWW2+t0mslJCTg6+uLs7Ps5yFEtel0cMv78MlWSNsN69+GG6erTlW/HVoBe74DnV67NHWNzTQ9XRyZObIj4+bHsXBzEjd1CKF7E786CisuZ+bvB0jJukBDH1f+b5j0vFHBYnNw2rRpw5AhQ5g0aRJxcXFs2rSJqVOnMnr0aEJDQwE4deoUERERxMXFVXrs0aNHWb9+PQ888MDfnvfXX39l7ty57N27l6NHjzJ79mxef/11HnnkEUu9FSHsn2ewtq8RwPq3IHWn2jz12YXzsPwJ7Th6CjTqWqWH9WsVwF3dGmE2w9M/7OZCsdFyGcVVbTySyVdbkwF4646OeDhXeyxB1AKL9sFZvHgxERERDBw4kJtuuok+ffrw2WefVXy/pKSEQ4cOUVBQuRPn/PnzadSoEYMGDfrbczo6OjJr1iyio6OJjIxkzpw5vPvuu8yYIb08hLgu7Udql6vMRlj6IJQUqk5U/5SvmspN1XaA7//vaj38/4a1JcjLmcTMfN7+Uy5VqZBbWMLTZZemxkY3lu0YFNKZr7a+2k7l5OTg7e1Ndna2zMcR4lL5Z+GTnloDwF6PwKBXVSeqX3Z9C0sng84AE/+ERt2u/Zj/seZgBhMWbgPgy4k96NtS5n7UpWd+2M2321MI93Pj98f64i6jN7WqOp/fsheVEOIi9wZw64fa8eaPpQFgXTqXBL+VbaHR/9kaFTcAN0YEcl/PxgBM+24XZ/Okv1Fd+XNfGt9uT0Gng7fv7CTFjWJS4AghKms9FCLvBczw02TZq6ouGEvhp39CcS6E9dSWhV+H/xvWhpaBHpzJLeKZH3dftRGqqB2p5y/w1A+7AXigT1N6NJVJ3qpJgSOE+LshM8G3KWSnwC9TtbkhwnI2vqftNeXkCbfPAcP1/ebv4mjgw7s742TQ89eBDL7aeqKWgorLKTWaeHxJAtkXSujYyJunBkeojiSQAkcIcTkuXnDHfNA7ap10t81Vnch+ndwOa2dqx8PeAd8mtfK0bUK8eGao9kH76m8HOJyeWyvPK/7uo9VHiUvKwsPZgY/u7oyTg3y0WgP5WxBCXF7DLjDoFe34j3/D6V1q89ijgiz4YYK2cq39SOh4V60+/YReTejXKoCiUhOPfrOTwhJZOl7bth4/y0erjwDw2m3tadzAXXEiUU4KHCHElUU9CK1v0rocfz8BimQUoNaYTFrn6PPJ2qjNsHe1pou1SK/X8fadnWjg7sTBtFxe+GWvzMepRefyi3l8SQImM9zRtRHDIxuqjiQuIQWOEOLKdDqtk65XI8g6BsunyXyc2rLhHTjyJzi4wF1fgquPRV4mwNOZD0Z3Rq+D77afZMk22YuvNhhNZqZ9l0BaTiHNAtx56dZ2qiOJ/yEFjhDi6tz84I55Wm+WPd/JfJzacHQVrHlNOx72LoR0tOjL9Wnpz5ODWgMw45d9JKSct+jr1QfvrTzMmkNncHbQ89HdnWVJuBWSAkcIcW3hPSHmRe14xbOQuEFpHJt2PgV+fAAwQ5dx0HlMnbzsw/2bM6htEMVGEw9/FS/9ca7Df/ec5uM1RwF4Y2RH2oV6K04kLkcKHCFE1fR6BDrcBaZS+G4snJOlx9VWWgTfj4MLWRDSCYa+WWcvrdPpePuuTjTzdyc1u5BHvtlJqdFUZ69vLw6m5fCv77UJ9w/0acqIzjLvxlpJgSOEqBqdTutyHBKpfUAvuQeK8lSnsh1ms9ZT6FQ8uPjAXV+Ao0udRvByceTT+7ri5mRg87GzvLHiYJ2+vq07X1DM5C/iKSg20rtFA54dKv1urJkUOEKIqnN0hdFfg3sgpO+Fnx+SScdVtfY/2hwmnQHuXFBr/W6qq1WQJ2/eoc35+XxDIotjZSSuKkqNJh75ZifJWQU08nXl47u74GCQj1BrJn87Qojq8W4Io77SmgAeWKZ9cIur2/UtrCv7Od38LjQfoDTOzR1DeTymJQDP/7yXNQczlOaxdmazmed/2ceGI5m4OOr57L5u+Lo7qY4lrkEKHCFE9YVHaR/UoH1wb1+gNo81S9oEv0zRjns/Dl3Hq0xT4bGBLbmjayNMZpjy9Q72nspWHclqfbjqKN/EJaPTwfujImkbevVdrIV1kAJHCFEzXcbCDU9px79Ng/3L1OaxRplH4dsxYCqBtsNh4AzViSrodDpev60DvVs0oKDYyISF2zh1/oLqWFZnSVwy7/11GICXb23HkPYhihOJqpICRwhRczf+n7bU2WzSlj4nbVSdyHpkn4Svbtd2Y2/YDW6bA3rr+l+uk4Oe2fd2pXWQJ2dyi5iwII7sghLVsazGX/vT+ffSPQBMvbEF90U3URtIVIt1/dcmhLAtOp3WqC7iZjAWwTd3Q9oe1anUy02DRbfC+RPg1wzu/kaboG2FvFwcmT+hO4GezhxOz2Ps/FhyCqXIiT9xjqnf7MBkhju7NuLJQa1URxLVJAWOEOL6GBxg5FwI7wVFOfDVSMg8ojqVOvmZ8MVwbWsL73AYuww8AlWnuqqGPq58MbEHvm6O7DqZzbj5ceTW4yJnZ/I5xi+Io7DExI2tA3j99g7oanmfMGF5UuAIIa6fo6s2ShHUHvLSYcFNkHFAdaq6V5AFX4yAMwfBMxTGLQOfMNWpqiQi2IuvHojC29WRncnnmbBgG/lFpapj1bn4E1ncNy+O3MJSejTxY9aYLjjKcnCbJH9rQoja4eoD9/2sFTn5GbBwGJzerTpV3blwXhu9St+j9Qka9yv4NVWdqlrahXqz+IEovFwc2H7iHBMWbqOguP4UOduSshg7L468olJ6NvNj4f3dcXOSPaZslRQ4Qoja4xGgfbCHRELBWVh0s9a5197lZWjvNXUHuPrB2F/Av4XqVDXSvqE3X06MwtPZgbjELMYv2FYv5uRsPX6WcfPjyC/rUrxgfA8pbmycFDhCiNrl5qddmmnUAwqzYdFwSN6qOpXlnE+G+UO0ydXuAdp7D2qrOtV16RTmw6KJPSqKnNFztnIm134351xzMIMJC7ZRUGykb0t/5o3rjquTQXUscZ2kwBFC1D4Xb7jvJ2jcB4pztUm3+35Wnar2pe6EuTFlE4rD4P4/ILiD6lS1oku4L99M7om/hxP7T+dwx6ebOXbG/vYeWxKXzANfbOdCiZF+rQL4fGw3XByluLEHUuAIISzD2RPGfA+thkBpobaL9qYP7GfvqoP/1SZT56VDYDutuGnQXHWqWtW+oTffP9iLRr6unDhbwO2fbGbzsUzVsWqF0WTmjRUHefanPRhNZm7v0lCKGzsjBY4QwnKc3LTNObtP0v688gX4aRIUF6jNdT1MJlj7hrabekkBNLsR7l+h7dFlh5r6u7P04d50Dvch+0IJY+fF8cWWJMw2XKjmFJYw6YvtzF57DNCa+L1zZyecHOQj0Z7ozLb8r7SGcnJy8Pb2Jjs7Gy8v2VNECIszmyF2DvzxbzAbtcs4dy6yvRGPgixtX6lD/9X+3G0iDH0DDI5qc9WBwhIjT/2wm193pQJwW+eGvHZbe5ubiLsvNZtHvt7J8cx8nB30vDGyIyM622dxao+q8/ktBY4UOELUncQN8P14KMgEJw+tC3KnUapTVc2JzfDjJMg5CQYnLXuX+1SnqlNms5l5GxOZ+ftBjCYzzQPc+WB0Z9o39FYd7ZrMZjNfbT3BK78doLjURIi3C3Pu60rHRj6qo4lqkALnGqTAEUKh7FPaZaoTm7Q/t7sNbnob3P3V5rqSkkJYOxM2f6jtueXXDEbOg4ZdVCdTZuvxszz6zU4ycotwNOh4PKYVk29oZrUN8U5nX+CZH/ew/vAZAAZGBPL2nZ3wdXdSnExUlxQ41yAFjhCKmYyw/m1Y94Z2ycqtAQyeCR3v0va3shZJm+DXx+Bs2dYTHUfDsLe1CdT13Ln8Yp79aTd/7EsHoE2IF2+M7GBVIyJGk5mvY0/w5h+HyC0sxclBz9ODWzOxT1PZesFGSYFzDVLgCGElUnfCL1Mhfa/257Ce2pyW0Eilscg+qU2I3vuj9mePYLj5XYgYpjaXlTGbzfy44xSvLN9P9oUSdDq4q2sYTw5uRaCni9JscYlZvLx8H3tP5QBab5937uxEi0APpbnE9ZEC5xqkwBHCipQWa5d/NryjrUoC7bJV/+kQ0Lpus+Smw8b3YPt8bXd0dNB1PMTMAFffus1iQzLzinhl+X5+SdAmILs7GRjfuwkP9GlW55eB9p7K5p0/D7HmkHY5ytPFgacGt2ZMVGMMehm1sXVWUeC89tpr/PbbbyQkJODk5MT58+ev+Riz2cyMGTP4/PPPOX/+PL1792b27Nm0bNmy4pysrCweeeQRfv31V/R6PSNHjuSDDz7Aw6PqVbkUOEJYoexT8NcM2PN92R06aH0TRD8MjXtb9tJVxkHY+gns/lbr2QNak8Ihr0NIJ8u9rp2JP5HFy8sPsCvlPKAVOqO6h3NfdGOa+rtb7HVNJjMbj2by+YbjbDii9ekx6HXc1S2Maf9oRYCns8VeW9QtqyhwZsyYgY+PDydPnmTevHlVKnDeeOMNZs6cyaJFi2jatCnPP/88e/bsYf/+/bi4aMOdQ4cO5fTp08yZM4eSkhImTJhA9+7d+frrr6ucTQocIaxY+j5Y8zocXH7xPv/W0Gk0tB8Jvo1r53Xyz8KBZbDrG0iJvXh/w24w4Dlo1t+65gPZCJPJzMoD6Xy46gj7UnMq7u/Twp9bI0MZ0j4YL5faWVZ/NCOP33af5vv4FE6euwCAXgc3dwzl8ZiWNAuQy1H2xioKnHILFy7k8ccfv2aBYzabCQ0N5cknn+Rf//oXANnZ2QQFBbFw4UJGjx7NgQMHaNu2Ldu2baNbt24ArFixgptuuomTJ08SGhpapUxS4AhhA84cgq2zYdcSKL1w8f6ANtAyBsKitGLEM7hqhciFc3BqB5zcBsdWa1/NJu17On3ZaNEUCI+WwqYWmM1m1h0+w6LNSaw9fKaigbWjQUeXcF9uaBVA53Af2jf0rlLBYzabSc0uJCH5PNuSslh/5AzHz+RXfN/T2YGRXRsxsU9TwvzcLPW2hGLV+fy2mg5NiYmJpKWlERMTU3Gft7c3UVFRbNmyhdGjR7NlyxZ8fHwqihuAmJgY9Ho9sbGx3HbbbZd97qKiIoqKLm4Ul5OTc9nzhBBWJKA13PI+/ONl2P+LVugkb4YzB7QbH2nnOXtDg2baRGA3P3B0BXTaHJqCLMg/A1nHta//K6gDdLwTOtwFXiF1+Obsn06no3/rQPq3DiT5bAHLdp3i54RUjmbkEZuYRWxiVsW5QV7OhPm6EejljKezIy6OekpNZopKTWTlF5ORW0jimXzyi42VXsPRoCO6uT8jIkMZ2j5ENsgUlVhNgZOWlgZAUFBQpfuDgoIqvpeWlkZgYGCl7zs4OODn51dxzuXMnDmTl156qZYTCyHqhIuX1lCvy31awXJsNSRtgJRtkLEfirK11VhV4dtE2+U8vCe0HAQ+YRaNLjThDdyYOqAlUwe0JCkznw1HzrDl+Fl2n8zm5LkLpOcUkZ5z7d3KHfQ6WgZ50qOJLz2aNuCGVv541tLlLmF/qlXgPPvss7zxxhtXPefAgQNERERcV6jaNn36dKZNm1bx55ycHMLC5H9sQtgcNz/ocId2A60J37lEOHtMG6G5kAWlZR+Uekdw9dF67Pg1Bb/mWrEklGri704Tf3fui24CwPmCYk6cLSA5q4Cs/GLyikopLDFi0OtwNOhp4O6Ev4czjRu40cTf3WqbCQrrU60C58knn2T8+PFXPadZs2Y1ChIcHAxAeno6ISEXh4rT09OJjIysOCcjI6PS40pLS8nKyqp4/OU4Ozvj7Cyz6IWwO44uENhGuwmb5OPmhI+bE53CfFRHEXamWgVOQEAAAQEBFgnStGlTgoODWbVqVUVBk5OTQ2xsLA899BAA0dHRnD9/nvj4eLp27QrA6tWrMZlMREVFWSSXEEIIIWyPxcb6kpOTSUhIIDk5GaPRSEJCAgkJCeTl5VWcExERwdKlSwFtQtrjjz/Oq6++yrJly9izZw9jx44lNDSUESNGANCmTRuGDBnCpEmTiIuLY9OmTUydOpXRo0dXeQWVEEIIIeyfxSYZv/DCCyxatKjiz507dwZgzZo19O/fH4BDhw6RnZ1dcc7TTz9Nfn4+kydP5vz58/Tp04cVK1ZU9MABWLx4MVOnTmXgwIEVjf4+/PBDS70NIYQQQtgg2apB+uAIIYQQNqE6n98yHV0IIYQQdkcKHCGEEELYHSlwhBBCCGF3pMARQgghhN2RAkcIIYQQdkcKHCGEEELYHSlwhBBCCGF3pMARQgghhN2RAkcIIYQQdsdiWzVYs/LmzTk5OYqTCCGEEKKqyj+3q7IJQ70scHJzcwEICwtTnEQIIYQQ1ZWbm4u3t/dVz6mXe1GZTCZSU1Px9PREp9PV6nPn5OQQFhZGSkqK7HP1P+Rnc3Xy87k6+flcnfx8rkx+NldnSz8fs9lMbm4uoaGh6PVXn2VTL0dw9Ho9jRo1suhreHl5Wf0/FFXkZ3N18vO5Ovn5XJ38fK5MfjZXZys/n2uN3JSTScZCCCGEsDtS4AghhBDC7kiBU8ucnZ2ZMWMGzs7OqqNYHfnZXJ38fK5Ofj5XJz+fK5OfzdXZ68+nXk4yFkIIIYR9kxEcIYQQQtgdKXCEEEIIYXekwBFCCCGE3ZECRwghhBB2RwqcWjRr1iyaNGmCi4sLUVFRxMXFqY5kNdavX88tt9xCaGgoOp2On3/+WXUkqzFz5ky6d++Op6cngYGBjBgxgkOHDqmOZTVmz55Nx44dK5qQRUdH8/vvv6uOZZX+85//oNPpePzxx1VHsQovvvgiOp2u0i0iIkJ1LKty6tQp7r33Xho0aICrqysdOnRg+/btqmPVCilwasm3337LtGnTmDFjBjt27KBTp04MHjyYjIwM1dGsQn5+Pp06dWLWrFmqo1iddevWMWXKFLZu3crKlSspKSlh0KBB5Ofnq45mFRo1asR//vMf4uPj2b59OwMGDGD48OHs27dPdTSrsm3bNubMmUPHjh1VR7Eq7dq14/Tp0xW3jRs3qo5kNc6dO0fv3r1xdHTk999/Z//+/bzzzjv4+vqqjlY7zKJW9OjRwzxlypSKPxuNRnNoaKh55syZClNZJ8C8dOlS1TGsVkZGhhkwr1u3TnUUq+Xr62ueO3eu6hhWIzc319yyZUvzypUrzf369TM/9thjqiNZhRkzZpg7deqkOobVeuaZZ8x9+vRRHcNiZASnFhQXFxMfH09MTEzFfXq9npiYGLZs2aIwmbBF2dnZAPj5+SlOYn2MRiNLliwhPz+f6Oho1XGsxpQpUxg2bFil/wcJzZEjRwgNDaVZs2aMGTOG5ORk1ZGsxrJly+jWrRt33nkngYGBdO7cmc8//1x1rFojBU4tyMzMxGg0EhQUVOn+oKAg0tLSFKUStshkMvH444/Tu3dv2rdvrzqO1dizZw8eHh44Ozvz4IMPsnTpUtq2bas6llVYsmQJO3bsYObMmaqjWJ2oqCgWLlzIihUrmD17NomJifTt25fc3FzV0azC8ePHmT17Ni1btuSPP/7goYce4tFHH2XRokWqo9WKermbuBDWasqUKezdu1fmCfyP1q1bk5CQQHZ2Nj/88APjxo1j3bp19b7ISUlJ4bHHHmPlypW4uLiojmN1hg4dWnHcsWNHoqKiaNy4Md999x0TJ05UmMw6mEwmunXrxuuvvw5A586d2bt3L59++injxo1TnO76yQhOLfD398dgMJCenl7p/vT0dIKDgxWlErZm6tSpLF++nDVr1tCoUSPVcayKk5MTLVq0oGvXrsycOZNOnTrxwQcfqI6lXHx8PBkZGXTp0gUHBwccHBxYt24dH374IQ4ODhiNRtURrYqPjw+tWrXi6NGjqqNYhZCQkL/9ktCmTRu7uYwnBU4tcHJyomvXrqxatariPpPJxKpVq2SegLgms9nM1KlTWbp0KatXr6Zp06aqI1k9k8lEUVGR6hjKDRw4kD179pCQkFBx69atG2PGjCEhIQGDwaA6olXJy8vj2LFjhISEqI5iFXr37v23lhSHDx+mcePGihLVLrlEVUumTZvGuHHj6NatGz169OD9998nPz+fCRMmqI5mFfLy8ir91pSYmEhCQgJ+fn6Eh4crTKbelClT+Prrr/nll1/w9PSsmLfl7e2Nq6ur4nTqTZ8+naFDhxIeHk5ubi5ff/01a9eu5Y8//lAdTTlPT8+/zdVyd3enQYMGMocL+Ne//sUtt9xC48aNSU1NZcaMGRgMBu6++27V0azCE088Qa9evXj99de56667iIuL47PPPuOzzz5THa12qF7GZU8++ugjc3h4uNnJycnco0cP89atW1VHshpr1qwxA3+7jRs3TnU05S73cwHMCxYsUB3NKtx///3mxo0bm52cnMwBAQHmgQMHmv/880/VsayWLBO/aNSoUeaQkBCzk5OTuWHDhuZRo0aZjx49qjqWVfn111/N7du3Nzs7O5sjIiLMn332mepItUZnNpvNimorIYQQQgiLkDk4QgghhLA7UuAIIYQQwu5IgSOEEEIIuyMFjhBCCCHsjhQ4QgghhLA7UuAIIYQQwu5IgSOEEEIIuyMFjhBCCCHsjhQ4QgghhLA7UuAIIYQQwu5IgSOEEEIIuyMFjhBCCCHszv8DhKiQqwkbrzAAAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"y1 = np.sin(x) # Sinus Werte mittels x berechnen\n",
|
||
"y2 = np.cos(x) # Kosinus Werte mittels x berechnen\n",
|
||
"\n",
|
||
"plt.plot(x, y1) # Plotte den Sinus\n",
|
||
"plt.plot(x, y2) # Plotte den Kosinus\n",
|
||
"\n",
|
||
"plt.show() # Zeige das Diagramm"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "c1e5749a-8f46-41ae-817a-19e5103a9a7a",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-d1d50ca1d203ac29",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe - Erster eigener Plot - Squareroot\n",
|
||
"\n",
|
||
"*3 Punkte*\n",
|
||
"\n",
|
||
"Analog zur vorherigen Erklärung plotten Sie im Folgenden die Funktion **Square Root**, mathematisch definiert als $f(x) = \\sqrt{x}, \\quad x \\geq 0$. \n",
|
||
"\n",
|
||
"Gehen Sie dabei wie folgt vor: \n",
|
||
"1. Definieren Sie einen **geeigneten** [Linspace](https://numpy.org/doc/stable/reference/generated/numpy.linspace.html#numpy-linspace) für den Zahlenraum von `0` bis `100`. (Tipp: Achten Sie darauf, dass die Quadratwurzel nur für nicht-negative Zahlen definiert ist.) \n",
|
||
"2. Berechnen Sie die Werte für die Quadratwurzel mithilfe der Funktion [np.sqrt](https://numpy.org/doc/stable/reference/generated/numpy.sqrt.html#numpy.sqrt). \n",
|
||
"3. Plotten Sie das Ergebnis mit `plt.plot` und geben Sie den Plot mit `plt.show()` aus.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 31,
|
||
"id": "c36ff699-9c30-448c-9d97-0a75e00888fd",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-bae73642cf0a866a",
|
||
"locked": false,
|
||
"points": 3,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAh8AAAGdCAYAAACyzRGfAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAOLZJREFUeJzt3Xl4VOXB/vF7soesQEhCyGRhk32RALKIIrhvuKAiWkSrtcUFaV+VutUq4vJ7rbW1WKxIVRCXKioqvhYUpEBCwr4HAiRANpZkEkImycz5/RGcGkXZZubM8v1cV66rOXPI3NcDzdye85znsRiGYQgAAMBLQswOAAAAggvlAwAAeBXlAwAAeBXlAwAAeBXlAwAAeBXlAwAAeBXlAwAAeBXlAwAAeFWY2QF+yOl0av/+/YqLi5PFYjE7DgAAOAmGYaimpkZpaWkKCfn5axs+Vz72798vq9VqdgwAAHAaSkpKlJ6e/rPn+Fz5iIuLk9QcPj4+3uQ0AADgZNhsNlmtVtfn+M/xufLx3a2W+Ph4ygcAAH7mZKZMMOEUAAB4FeUDAAB4FeUDAAB4FeUDAAB4FeUDAAB4FeUDAAB4FeUDAAB4FeUDAAB4FeUDAAB41SmXj6VLl+rKK69UWlqaLBaL5s+f3+J1wzD0+OOPq3379oqOjtbo0aNVWFjorrwAAMDPnXL5OHLkiPr27atXXnnluK8///zzevnll/Xqq68qNzdXMTExuvjii1VfX3/GYQEAgP875b1dLr30Ul166aXHfc0wDL300kt69NFHdfXVV0uS3nzzTaWkpGj+/Pm66aabziwtAADwe26d87Fr1y6VlZVp9OjRrmMJCQkaPHiwVqxYcdw/Y7fbZbPZWnwBAAD321lZq+cXbtWMb3aamsOtu9qWlZVJklJSUlocT0lJcb32Q9OnT9eTTz7pzhgAAOAYW32jFqwr1QcFJVpdXCVJSoqN1C/PzVZ4qDnPnbi1fJyOqVOnasqUKa7vbTabrFariYkAAPBvDqeh5TsP6IOCvVq4sUz2JqckKTTEovO6ttP1A9J14o3vPcet5SM1NVWSVF5ervbt27uOl5eXq1+/fsf9M5GRkYqMjHRnDAAAgtKuA0f0QUGJPly9T6XV/33Qo0tyrMbmpGtMvw5Kjo8yMWEzt5aP7OxspaamatGiRa6yYbPZlJubq1//+tfufCsAACCppr5Rn60v1QcFe5W/57DreHxUmK7u10HXD0hXn/QEWSxmXuto6ZTLR21trXbs2OH6fteuXVq7dq3atGmjjIwMTZ48WU8//bS6dOmi7OxsPfbYY0pLS9OYMWPcmRsAgKDldBpavvOgPigo0cJNZapvbL6tEmKRRnRtp7EDrBrVPVlR4aEmJz2+Uy4f+fn5GjlypOv77+ZrTJgwQbNnz9aDDz6oI0eO6K677lJVVZWGDx+uhQsXKirK/Ms8AAD4s+KDdXq/oET/Ktir/d+7rdKpXYzG5lh1Tf8OSvGB2yonYjEMwzA7xPfZbDYlJCSourpa8fHxZscBAMBU9Y0OfbGxVO+t2qsVRQddx+OiwnRV3zRdPyBd/ayJpt9WOZXPb9OfdgEAAC0ZhqH1e6v1Xn6JPlm3XzX1TZIki0Ua3jlJY3OsuqhHis/eVjkRygcAAD7i0JEGfbRmn97PL9HWshrX8fTW0Ro7wKrrBnRQeutWJiZ0D8oHAAAmcjgNfVtYqffyS/TV5nI1OppnQ0SEhejSXqm6IceqIR3bKiTEd55WOVOUDwAATPDd5NEPCva2WJOjV4d43Zhj1VV9OyihVbiJCT2H8gEAgJccbXBo4aZSvbuqRCuLDrmOJ7YK15h+HTQ2J1090xJMTOgdlA8AADyoxeTRtftVY285efTGgVaN7u6/k0dPB+UDAAAP+LnJozfkWHXdgHR1SIw2MaF5KB8AALiJ02noPzsPaF5eif5vc9mPJo/emGPVOQE2efR0UD4AADhD5bZ6vZ9fonfzS1Ry6KjreO8OCbphoFVX9UkL2Mmjp4PyAQDAaXA4DX2zrULv5JXo620Vcjibr3LERYXpmv4ddONAa1BMHj0dlA8AAE7B3sN1ei9/r97PL2nxiOzArNa6aWCGLuvdXtERwTN59HRQPgAAOIFGh1OLtpTrnbwSLS2s1He7orVuFa5rz07XTQOt6pISZ25IP0L5AADgJ+w5eETzVpXo/fy9OlBrdx0f2qmtbhqUoYt7pigyjKscp4ryAQDA99ibHPpyU7nm5RVr+c7/7iKbFBup6wc0X+XISooxMaH/o3wAACBpR0WN3skr0Yer9+pwXaOk5oXARnRpp3GDrBrVPUXhoSEmpwwMlA8AQNA62uDQ5xtKNW9VsVbtPuw6nhofpRty0nXDQGtA7CLraygfAICgU1heozm5xfpw9V7Z6puXOw8NsWjkWckaN8iq87q2UxhXOTyG8gEACAr2JocWbizTnJXFytv9303d0ltH66aBVo3NsSolPsrEhMGD8gEACGi7DxzRO3nFer9grw4daZDUfJVjVLdkjT8nU+d2Tgr65c69jfIBAAg4363LMSe3WN8WHnAdT42P0rhBGbpxoFWpCVzlMAvlAwAQMPZXHdW8vGLNW1WiiprmdTksFum8ru00fnCmRp7FXA5fQPkAAPg1h9PQ0u2VmpO7R4u3VujYFitKio3QDTlWjRuUIWsbnljxJZQPAIBfqqip1/v5ezU3t1j7qv67k+yQjm01/pwMXdQjVRFhXOXwRZQPAIDfMAxDK3Ye1JzcYn25qUxNxy5zJESH6/oB6Ro3KEOdk2NNTokToXwAAHxedV2j3i8o0dzcYhUdOOI6fnZGosYPztTlfdorKpw9VvwF5QMA4LM27qvWWyv26ON1+1Tf6JQkxUaG6Zr+HXTz4Ax1bx9vckKcDsoHAMCn2Jsc+mJDmd5csVuri6tcx7ulxunWIZka06+DYiL5+PJn/O0BAHzCvqqjmpu7R/PySnTw2GJgYSEWXdq7vX4xJFM5ma1lsbAYWCCgfAAATGMYhpbtOKA3V+zRoi3lrsdkU+OjdPPgDN00yKrkOBYDCzSUDwCA11UfbdS/Cvbq7ZV7WkwgHdqprX4xJFOju6ewGFgAo3wAALxmS6lNb67Yo/lr9uloo0NS8wTS687uoFuHZKpzcpzJCeENlA8AgEc1NDm1cFOZ3lqxW6t2H3Yd75oSq1uHZOma/h0UywTSoMLfNgDAI8qq6zU3d4/m5pXoQG3zPithIRZd3DNVtw7J1ODsNkwgDVKUDwCA2xiGoYI9h/XG8t1auLFMjmMzSJPjInXz4AyNG5ShlHgmkAY7ygcA4IzVNzq0YH2pZi/fpY37bK7jg7LbaMKQLF3UM0XhTCDFMZQPAMBpK6uu15zcPZqbW+xamyMyLETX9O+gCUOzWIEUx0X5AACcEsMwtLq4SrOX79YXG0pdm7ulJUTp1iFZummgVa1jIkxOCV9G+QAAnBR7k0OfrS/V7OW7tX5vtev4oOw2mjg0Sxf2YG0OnBzKBwDgZ1XY6vV2brHm5u7RgdrmWysRYSEa0y9NE4ZmqWdagskJ4W8oHwCA41pTfFizl+/WZ+v/e2slNT5Ktw7J1E0DrWobG2lyQvgrygcAwKWhyanPN5TqjeW7ta6kynV8YFZr3TY0m6dW4BaUDwCAKmvsmpO7R3Nyi1VZ07wgWERoiK7sm6aJw7LUqwO3VuA+lA8ACGJby2x6/dtd+njtfjU4nJKaFwS79ZxMjRucoSRurcADKB8AEGScTkNLtlfq9WW7tGzHAdfxftZE3T48W5f2SuXWCjyK8gEAQeJog0MfrtmrWct2aWdl8zb2IRbp0l7tdfvwbA3IbG1yQgQLygcABLgKW73eXLFHc3L36HBdoyQpLjJMNw60asLQLFnbtDI5IYIN5QMAAtTGfdWatWyXPl2/X42O5kdlrW2iNXFotsbmpCsuKtzkhAhWlA8ACCBOp6HFWyv0j2VFWll0yHU8J7O1fnluti7skarQELaxh7koHwAQAOoamvRBwV698Z/d2nWgeT5HaIhFl/durzuGZ6uvNdHcgMD3UD4AwI+VVddr9vLdeievWNVHm+dzxEeFadzgDE0YkqW0xGiTEwI/RvkAAD+0tcymmUuL9Mna/a6lz7PattLtw7N13dnpionk1zt8F/86AcBPGIah5TsPaubSIi3ZXuk6Pii7je48t6Mu6JbMfA74BcoHAPi4JodTn20o1cylRdq03ybpv+tz3Dmio/oxnwN+hvIBAD6q1t6kd1eVaNayXdpXdVSSFB0eqhty0nXH8I7KaMv6HPBPlA8A8DEVtnq9sXy35qzcI1t9kyQpKTZCE4Zk6ZZzMtU6JsLkhMCZoXwAgI8oLK/RzKVFLTZ565gUo1+e21HXnt1BUeGhJicE3IPyAQAmMgxDubsOaebSIi3eWuE6npPZWneN6KjR3VMUwiRSBBi3lw+Hw6E//OEPevvtt1VWVqa0tDTddtttevTRR2Wx8H8gAJCaJ5Eu3FSm15YWad3eakmSxSJd3CNVd47oyCZvCGhuLx/PPfecZsyYoX/+85/q2bOn8vPzNXHiRCUkJOi+++5z99sBgF+pb3Tog4K9mrm0SMWH6iRJkWEhun5Aun55bkdlJ8WYnBDwPLeXj+XLl+vqq6/W5ZdfLknKysrSO++8o7y8PHe/FQD4DVt9o+asLNbry3bpQK1dktS6Vbh+MSRLvxiSqbaxkSYnBLzH7eVj6NChmjlzprZv366uXbtq3bp1WrZsmV588cXjnm+322W3213f22w2d0cCANNU1tj1xn926a0Ve1Rjb35ypUNitO48N1s3DLSqVQRT7xB83P6v/uGHH5bNZlO3bt0UGhoqh8OhadOmafz48cc9f/r06XryySfdHQMATFV8sE4zv92p9/L3qqGp+cmVLsmxuvu8TrqqX5rCQ0NMTgiYx+3l47333tOcOXM0d+5c9ezZU2vXrtXkyZOVlpamCRMm/Oj8qVOnasqUKa7vbTabrFaru2MBgFdsKbXp1SU79em6/Tq25Yr6WRP1m/M78eQKcIzFMAzDnT/QarXq4Ycf1qRJk1zHnn76ab399tvaunXrCf+8zWZTQkKCqqurFR8f785oAOAxq3Yf0t++3qGvt/13z5URXdvpN+d30uDsNjzth4B3Kp/fbr/yUVdXp5CQlpcTQ0ND5XQ63f1WAGAqwzC0eGuFZnyzU/l7Dktq3nPlst7tdfd5ndSrQ4LJCQHf5PbyceWVV2ratGnKyMhQz549tWbNGr344ou6/fbb3f1WAGCKJodTC9aX6tUlO7W1rEaSFBEaousGpOtXIzoqi8dlgZ/l9tsuNTU1euyxx/TRRx+poqJCaWlpGjdunB5//HFFRJx4PwJuuwDwVfWNDr2fX6K/Ly3S3sPNG73FRITqlnMydcfwbCXHR5mcEDDPqXx+u718nCnKBwBfU9fQpLm5xZq5tEgVNc1LA7SNidDtw7N1y+BMJbQKNzkhYD5T53wAQKCoqW/Umyv26PVlu3ToSIMkKS0hSr86r5NuyLEqOoKN3oDTQfkAgB+oqmvQrP/s1uz/7HJtaZ/RppUmjeyka/qnKyKMNTqAM0H5AIBjKmvs+seyIr29Yo+ONDgkSZ3axeieCzrryj5pCmNhMMAtKB8Agl5p9VH9fUmR3skrlv3YaqTd28fr3gs665KeqSwMBrgZ5QNA0Co5VKcZS3bqg/y9anA0l46+1kTdd0FnXdAtmYXBAA+hfAAIOjsra/W3r3dq/tp9chxbA31Qdhvde0FnDe+cROkAPIzyASBo7Kio0cuLdujT9fv13SID53ZJ0j0jO2twx7bmhgOCCOUDQMA7XukY3T1Z91zQRf2siaZmA4IR5QNAwDpe6bioR4ruG9WFfVcAE1E+AAQcSgfg2ygfAAIGpQPwD5QPAH6P0gH4F8oHAL9F6QD8E+UDgN+hdAD+jfIBwG/sOnBEL/17uz5ZR+kA/BnlA4DP23u4Tn9ZtEMfrN7rWpGU0gH4L8oHAJ9VbqvXK1/v0Dt5xWp0NJeOC7ola8qFXSkdgB+jfADwOYeONOjVJTv1z+W7XbvMDuvcVlMuPEsDMlubnA7AmaJ8APAZ1Ucb9Y9vizRr2S4daXBIks7OSNTvLj5LQzslmZwOgLtQPgCY7oi9SbOX79bfl+yUrb5JktSrQ7x+e9FZOr9rO3aZBQIM5QOAaeobHXp75R7N+GanDh5pkCR1TYnVlAu76uKeqZQOIEBRPgB4XUOTU+/ml+iviwtVbrNLkrLattIDF3bVFX3SFBpC6QACGeUDgNc4nIbmr9mnP/17u/YePipJ6pAYrftGdda1Z6crPDTE5IQAvIHyAcDjDMPQoi0VeuHLbdpWXiNJahcXqXsv6KwbB1oVGRZqckIA3kT5AOBRq3Yf0nNfbFX+nsOSpPioMP36/M66bWiWoiMoHUAwonwA8IitZTa9sHCbFm2tkCRFhYdo4rBs3T2ikxJahZucDoCZKB8A3KrkUJ3+9NV2fbR2nwxDCg2x6IYcqyaP7qKU+Ciz4wHwAZQPAG5xoNauvy7eoTm5e1xLoV/eu71+e1FXdWwXa3I6AL6E8gHgjNTam/Ta0iL949si16qkwzq31UOXdFOf9ERzwwHwSZQPAKelocmpObl79NfFO1wLhPXukKCHLumm4V1YCh3AT6N8ADglhmHo8w1lev7LrdpzsE6SlJ0Uo99ddJYu7ZWqEBYIA3AClA8AJy1/9yFN+3yL1hRXSZKSYiP1wIVddEOOlQXCAJw0ygeAEyqqrNVzC7fqy03lkqTo8FDdNaKj7hrRUTGR/BoBcGr4rQHgJx2stevlRYWak1usJqehEIt040CrHhjdVck8NgvgNFE+APxIfaNDry/bpRnf7FStvXmL+5FntdPUy7qra0qcyekA+DvKBwAXp9PQh2v26X//b5tKq+slST3T4vXIZd01tDNPsABwD8oHAEnSt4WVeubzrdpSapPUvNvs7y7uqqv7duAJFgBuRfkAgtyOiho9/dkWfbOtUpIUFxWmSSObN36LCmfjNwDuR/kAgtThIw3686JCvbVyjxxOQ+GhFt1yTqbuu6CLWsdEmB0PQACjfABBptHh1Nsr9+ilfxeq+mijJOnCHin6/WXdlZ0UY3I6AMGA8gEECcMw9M22Sj312WYVVR6RJHVLjdNjV/TQMCaTAvAiygcQBLaXN8/rWLq9eV5H25gI/fais3TjQKtCmUwKwMsoH0AAO3SkQS/9e7vm5Ba75nXcPixbky7orPiocLPjAQhSlA8gADU0OfXmit16eVGhbPXNi4Rd3DNFUy/trizmdQAwGeUDCCCGYWjRlgpN+3yLdh1ontfRvX28Hruiu4Z2Yl4HAN9A+QACxM7KWj356WbXvI6k2Aj97qKzNDaHeR0AfAvlA/BzR+xN+sviHXp9WZEaHcfmdQzP1j0jOyuOeR0AfBDlA/BThmHok3X79cznW1Rus0uSzj+rnR6/ooc6tos1OR0A/DTKB+CHtpTa9MQnm5S365AkKaNNKz1+RQ+N6p4si4VbLAB8G+UD8CPVdY168attemvlHjkNKSo8RJPO76w7R3RkHxYAfoPyAfgBp9PQe/klev7LbTp0pEGSdFnvVD1yeQ91SIw2OR0AnBrKB+Dj1hQf1hOfbNL6vdWSpC7JsfrDVT1ZEh2A36J8AD7qQK1dz32xVe8X7JUkxUWG6f7RXTRhaJbCQ0NMTgcAp4/yAfgYh9PQ3LxiPb9wq2qOrU56/YB0PXjJWUqOizI5HQCcOcoH4EM27qvWIx9t0Lpjt1h6dYjXk1f10oDM1iYnAwD3oXwAPsBW36gX/2+73lyxW06j+RbL7y4+S7eck8nqpAACjkduHO/bt0+33HKL2rZtq+joaPXu3Vv5+fmeeCvAr323UNio/12i2cubi8dVfdO06LfnacLQLIoHgIDk9isfhw8f1rBhwzRy5Eh98cUXateunQoLC9W6NZeNge8rqqzV4x9v0rIdByRJHZNi9Mere2l4F55iARDY3F4+nnvuOVmtVr3xxhuuY9nZ2e5+G8Bv1Tc69LdvdurVb3aqweFURFiI7hnZWb86r6Miw1goDEDgc/ttl08++UQ5OTkaO3askpOT1b9/f7322ms/eb7dbpfNZmvxBQSqJdsrdfFLS/XyokI1OJw6r2s7ffXACN03qgvFA0DQcHv5KCoq0owZM9SlSxd9+eWX+vWvf6377rtP//znP497/vTp05WQkOD6slqt7o4EmK6yxq773lmjCbPytOdgnVLjozRj/NmaPXGgMtvGmB0PALzKYhiG4c4fGBERoZycHC1fvtx17L777tOqVau0YsWKH51vt9tlt9td39tsNlmtVlVXVys+Pt6d0QCvMwxD7xfs1bTPtqj6aKNCLNLEYdl64MKuio3kYTMAgcNmsykhIeGkPr/d/tuvffv26tGjR4tj3bt317/+9a/jnh8ZGanIyEh3xwBMt+vAEf3+ww1aUXRQktQzLV7PXttHvdMTTE4GAOZye/kYNmyYtm3b1uLY9u3blZmZ6e63AnxSo8OpmUuL9OdFhWpocioqPERTLuyq24dlK4xl0QHA/eXjgQce0NChQ/XMM8/ohhtuUF5enmbOnKmZM2e6+60An7Om+LCmfrhBW8tqJEnndknStDG9ldG2lcnJAMB3uH3OhyQtWLBAU6dOVWFhobKzszVlyhTdeeedJ/VnT+WeEeArau1N+n9fbtM/V+yWYUhtYiL02BXdNaZfB1ksLBQGIPCdyue3R8rHmaB8wN/8e3O5Hvt4o0qr6yVJ1/bvoEev6KE2MREmJwMA7zF1wikQLA7W2vWHTzfr03X7JUnWNtF65preOrdLO5OTAYBvo3wAp8gwDH22oVRPfLxJB480KDTEol8Oz9bk0V0VHcFCYQBwIpQP4BRU1NTr8fmbtHBTmSTprJQ4vTC2j/qkJ5obDAD8COUDOAmGYWj+2n168tPNqqprVFiIRb8Z2Vn3jOysiDAenwWAU0H5AE6grLpej3y0QYu2VkhqXizs+ev7qGcai4UBwOmgfAA/4bul0Z9asFk19U0KD7Xo/lFd9KvzOimcxcIA4LRRPoDj2Fd1VFM/3KCl2yslSX3TE/TC2L7qmhJncjIA8H+UD+B7DMPQvFUlmvbZFtXamxQRFqLfXthVdwxnaXQAcBfKB3BMha1eD/5rvb7Z1ny1Y0Bmaz1/fR91ahdrcjIACCyUD0DSgvX79ej8jaqqa1REWIgevPgsTRyWrdAQlkYHAHejfCCoVdU16PGPN+mTY6uU9uoQrz/d0E9dmNsBAB5D+UDQWrK9Ug9+sE7lNrtCQyyaNLKz7r2gM0+yAICHUT4QdOoamjTtsy2ak1ssSerYLkYv3tBP/ayJ5gYDgCBB+UBQKdhzSFPeW6c9B+skSbcNzdJDl3RjTxYA8CLKB4KCvcmhP/+7UK8u2SmnIbVPiNL/G9tXwzonmR0NAIIO5QMBb3t5je6ft1ZbSm2SpGvP7qAnruyphOhwk5MBQHCifCBgGYaht1bu0bTPtsje5FSbmAg9c00vXdKrvdnRACCoUT4QkA7W2vXgB+tdm8Gd17WdXhjbR8lxUSYnAwBQPhBwlmyv1G/fW6cDtXZFhIbo4Uu76bahWQphwTAA8AmUDwQMe5NDzy/cpteX7ZIkdUmO1cvj+qt7+3iTkwEAvo/ygYBQWF6j+743qfQXQzL1+8u6KyqcR2gBwNdQPuDXDMPQnNxiPbVgs2tS6QvX99Go7ilmRwMA/ATKB/xW9dFGPfTBei3cVCZJOrdLkv53bF8lxzOpFAB8GeUDfmltSZXumbtaew8fVXioRQ9d0k23D8tmUikA+AHKB/yKYRh6fdkuPfvFVjU5DVnbROuv485WX/ZlAQC/QfmA3zh8pEG/e3+da+2Oy3qn6tnr+ig+ipVKAcCfUD7gF/J3H9K976xRaXW9IsJC9NgVPXTL4AxZLNxmAQB/Q/mAT3M6Dc1YslMvfrVdDqeh7KQY/fXm/uqZlmB2NADAaaJ8wGcdrLVr8rtr9W3hAUnSmH5pevqa3oqN5J8tAPgzfovDJ60uPqxJc1artLpeUeEh+uNVvTQ2J53bLAAQACgf8Cnf7UT71ILNanQY6pgUoxm3DNBZqXFmRwMAuAnlAz6jrqFJv/9wg+av3S+p+WmW567rozieZgGAgEL5gE8oqqzV3W8XaHt5rUJDLJp6aTfdMTyb2ywAEIAoHzDdwo2l+t3761Vrb1K7uEi9cvPZGpTdxuxYAAAPoXzANE0Op57/cptmLi2SJA3KaqO/3tyfvVkAIMBRPmCKyhq77pm7Wrm7DkmS7hrRUf9z8VkKDw0xORkAwNMoH/C69Xur9Ku3ClRaXa/YyDC9cH0fXdq7vdmxAABeQvmAV81fs08P/Wu97E1OdWwXo5m35qhzcqzZsQAAXkT5gFc4nIaeW7jVNb/jgm7JeummfmwKBwBBiPIBj6uua9S989Zo6fZKSdKkkZ005cKzFBrCY7QAEIwoH/CowvIa3flmvnYfrFN0eKheGNtHV/RJMzsWAMBElA94zFeby/XAu2tVa29Sh8RozfzFAHajBQBQPuB+hmHor4t36H+/2i5JGpzdRn8bf7baxkaanAwA4AsoH3Cr+kaHfvf+Oi1YXypJmjAkU49e0YP1OwAALpQPuE1ljV13vpmvtSVVCgux6KkxvTRuUIbZsQAAPobyAbfYWmbTHbPzta/qqBKiw/XqLQM0pFNbs2MBAHwQ5QNn7OutFbpn7modaXAoOylGs24bqOykGLNjAQB8FOUDZ2T2f3bpjws2y2lI53Rso1dvGaDEVhFmxwIA+DDKB05Lk8OpPy7YrDdX7JEk3ZCTrqfH9FZEGBNLAQA/j/KBU1bX0KR7567Roq0Vslikhy/pprtGdJTFwoqlAIATo3zglByoteuO2au0bm+1IsNC9Oeb+umSXuxICwA4eZQPnLRdB45owqw8FR+qU+tW4frHhIEakNna7FgAAD9D+cBJWV18WHfMXqXDdY3KaNNKsycOVMd2sWbHAgD4IcoHTujLTWW67501sjc51Tc9Qa/fNlBJLJUOADhNlA/8rDdX7NYTn2ySYUijuiXrLzf3V6sI/tkAAE4fnyI4LsMw9KevtuvlxTskSeMGZeipq3sqjD1aAABnyOOfJM8++6wsFosmT57s6beCmzichh77eKOreEy5sKueuaYXxQMA4BYevfKxatUq/f3vf1efPn08+TZwo4Ymp6a8t1YL1pfKYpH+eHUv3XpOptmxAAABxGP/KVtbW6vx48frtddeU+vWPI7pD+oamvTLN/O1YH2pwkMtevmm/hQPAIDbeax8TJo0SZdffrlGjx79s+fZ7XbZbLYWX/C+qroGjf9HrpZur1R0eKj+MWGgruybZnYsAEAA8shtl3nz5mn16tVatWrVCc+dPn26nnzySU/EwEkqq67XL2blant5rRKiwzXrNhYPAwB4jtuvfJSUlOj+++/XnDlzFBUVdcLzp06dqurqatdXSUmJuyPhZ5QcqtPYvy/X9vJaJcdF6r1fDaF4AAA8ymIYhuHOHzh//nxdc801Cg0NdR1zOByyWCwKCQmR3W5v8doP2Ww2JSQkqLq6WvHx8e6Mhh/YdeCIbn5tpUqr65XZtpXevmOwrG1amR0LAOCHTuXz2+23XUaNGqUNGza0ODZx4kR169ZNDz300M8WD3hPYXmNbv5Hripr7OrULkZz7zxHKfEnvlIFAMCZcnv5iIuLU69evVoci4mJUdu2bX90HObYvN+mW1/P1cEjDeqWGqe37hisdnEslw4A8A5WOA0y6/dW6dbX81R9tFG9OsTrrdsHq3VMhNmxAABBxCvl45tvvvHG2+AECvYc1m2z8lRjb1L/jETNnjhICdHhZscCAAQZrnwEidyig5o4e5XqGhwalNVGsyYOVGwkf/0AAO/j0ycI5O8+5CoewzsnaeYvBrAzLQDANHwCBbjVxYd12xvNxePcLkl67Rc5igrniSMAgHnYpjSArd9bpQmv56nW3qQhHdtq5q0UDwCA+SgfAWrjvmrd8o9c1dibNCirjV6/LUfRERQPAID5KB8BaGtZ8zoetvomDchsrVkTBzLHAwDgMygfAaawvEbjX8vV4bpG9bUmajZPtQAAfAzlI4AUVdZq3GvNK5f26hCvN28fpLgo1vEAAPgWykeAKK0+qltfz9OBWru6t4/X23cMZgExAIBPonwEgMNHGnTr63naV3VUHZNi9PYdg5TYiiXTAQC+ifLh547Ym3Tb7FXaUVGr9glReuuXg9U2lk3iAAC+i/Lhx+xNDt39doHWlVSpdatwvXXHIHVIjDY7FgAAP4vy4accTkNT3l2nbwsPqFVEqN6YOEidk+PMjgUAwAlRPvyQYRh6dP5GfbahVOGhFs28NUf9rIlmxwIA4KRQPvzQ//u/bXonr1gWi/Tnm/preJcksyMBAHDSKB9+5s0Vu/XK1zslSdPG9NZlvdubnAgAgFND+fAj/95crj98skmS9NsLu+rmwRkmJwIA4NRRPvzE+r1VuvedNXIa0k0Drbrngs5mRwIA4LRQPvxAyaE63T47X0cbHRrRtZ2eGtNLFovF7FgAAJwWyoePq65r1MTZq1zLpv9t/NkKD+WvDQDgv/gU82GNDqfufrvAtXrpG7exQy0AwP9RPnyUYRh64pNNWlF0UDERoZp120ClJkSZHQsAgDNG+fBRb67Yo7m5zWt5vDyuv7q3jzc7EgAAbkH58EHfFlbqjws2S5KmXtpNo7qnmJwIAAD3oXz4mJ2VtfrNnNVyOA1dd3a67jy3o9mRAABwK8qHD6mua9Sd/8xXTX2TBmS21jPX8kgtACDwUD58hNNp6IH31qrowBF1SIzWq7cMUGRYqNmxAABwO8qHj/jL4h1avLVCkWEh+vutA9QuLtLsSAAAeATlwwd8va1CLy3aLkl6ekwv9eqQYHIiAAA8h/JhsuKDdbr/nTUyDGn84AyNzbGaHQkAAI+ifJjoaINDv3q7QLb6JvWzJurxK3uYHQkAAI+jfJjo0fkbtaXUprYxEZpxy9lMMAUABAXKh0n+VbBX/1q9VyEW6S8391f7hGizIwEA4BWUDxPsrKzVYx9vlCRNHt1VQzslmZwIAADvoXx4WX2jQ/fMXaO6BoeGdmqrSSM7mx0JAACvonx42TOfb3HN8/jTjf0UGsIKpgCA4EL58KKFG8v05oo9kqT/vaGvUuKjTE4EAID3UT68ZF/VUT34wTpJ0q9GdNT5ZyWbnAgAAHNQPrzA6TT02/fWylbfpL7WRP32orPMjgQAgGkoH14we/lurSw6pOjwUP35xn6KCGPYAQDBi09BD9tRUavnFm6VJD1yeXdlJcWYnAgAAHNRPjyo0eHUlPfWyt7k1Iiu7TR+cIbZkQAAMB3lw4P+9vVOrd9brfioMD1/XR9ZLDxWCwAA5cNDNuyt1l8WF0qSnhrTS6kJPFYLAIBE+fAIe5NDU95bqyanoct7t9dVfdPMjgQAgM+gfHjA35cUqbCiVkmxEXpqTC9utwAA8D2UDzfbWVmrvy7eIUl67IoeahMTYXIiAAB8C+XDjQzD0CMfbVCDw6nzurbjdgsAAMdB+XCj9wv2amXRIUWFh+hpbrcAAHBclA83OVBr17TPtkiSHhjdVdY2rUxOBACAb6J8uMnTCzar+mijerSP1x3Ds82OAwCAz6J8uMG3hZWav3a/QizS9Gt7KyyUYQUA4KfwKXmGmhxOPfnpZknSL4Zkqa810dxAAAD4OMrHGZqbV6wdFbVq3SpcD1zY1ew4AAD4PMrHGaiua9SfvtouSZpyYVclRIebnAgAAN9H+TgDLy8u1OG6RnVJjtW4QexYCwDAyXB7+Zg+fboGDhyouLg4JScna8yYMdq2bZu738Z0RZW1+ufy3ZKaVzJlkikAACfH7Z+YS5Ys0aRJk7Ry5Up99dVXamxs1EUXXaQjR464+61M9cznW9TkNHRBt2SN6NrO7DgAAPiNMHf/wIULF7b4fvbs2UpOTlZBQYFGjBjh7rczxbeFlfr3lgqFhVj0+8u6mx0HAAC/4vby8UPV1dWSpDZt2hz3dbvdLrvd7vreZrN5OtIZcTgNPb2geSXTW4dkqnNyrMmJAADwLx6dqOB0OjV58mQNGzZMvXr1Ou4506dPV0JCguvLarV6MtIZ+3jtPm0rr1FCdLjuH9XF7DgAAPgdj5aPSZMmaePGjZo3b95PnjN16lRVV1e7vkpKSjwZ6Yw0Opx66d+FkqRfnddRia0iTE4EAID/8dhtl3vuuUcLFizQ0qVLlZ6e/pPnRUZGKjIy0lMx3Oq9/BIVH6pTUmykbhuaZXYcAAD8ktvLh2EYuvfee/XRRx/pm2++UXZ2YGyyVt/o0F8W7ZAk3TOyk1pFeHy6DAAAAcntn6CTJk3S3Llz9fHHHysuLk5lZWWSpISEBEVHR7v77bxmXl6xymz1SkuI0rjBLCgGAMDpcvucjxkzZqi6ulrnn3++2rdv7/p699133f1WXmNvcujvS4skSb8Z2VmRYaEmJwIAwH955LZLoPlw9T6VVtcrJT5S1w/46fkrAADgxFgT/ASaHE797ZvmuR53jeikqHCuegAAcCYoHyfwybr9Kjl0VG1jIjRukG+vQQIAgD+gfPwMwzA089hcj9uHZ/OECwAAbkD5+Bn/2XFQW8tqFB0eqlsGZ5odBwCAgED5+Bn/WNZ81eOGnHQltAo3OQ0AAIGB8vETCstr9M22SlkszbdcAACAe1A+fsKs/+ySJF3UI0WZbWNMTgMAQOCgfBxH9dFGfbRmnyTpjuEdTU4DAEBgoXwcx/w1+1Tf6FTXlFgNzGptdhwAAAIK5eMHDMPQ3NxiSdLNgzJksVhMTgQAQGChfPzA6uLD2lZeo6jwEF1zNkupAwDgbpSPH5izsvmqx5V90pQQzeO1AAC4G+Xje6qPNuqzDaWSpJsHZ5icBgCAwET5+J6FG0tlb2qeaNrPmmh2HAAAAhLl43vmr9kvSbq6XwcmmgIA4CGUj2PKquu1ctdBSdLV/dJMTgMAQOCifBzzybp9MgxpYFZrpbduZXYcAAACFuXjmO/fcgEAAJ5D+VDzJnKbS20KC7Ho8t7tzY4DAEBAo3xIWrixTJI0oms7tY6JMDkNAACBjfIhadHWCknShT1STE4CAEDgC/ryUVlj17q9VZKkC7olmxsGAIAgEPTl4+ttFTIMqXeHBKXER5kdBwCAgBf05WPRlnJJ0qjuXPUAAMAbgrp81Dc69G3hAUnSqG7M9wAAwBuCunzk7jqkugaHUuIj1atDvNlxAAAICkFdPr4+9pTLBd2S2csFAAAvCerykbfrkCRpeOd2JicBACB4BG35qLU3aWuZTZKUk9Xa5DQAAASPoC0fa4oPy2lI6a2jecQWAAAvCtryUbDnsCQpJ5OrHgAAeFPQl48BWW1MTgIAQHAJyvLhcBpaU1wlSRqQwZUPAAC8KSjLx9Yym2rtTYqLDNNZqXFmxwEAIKgEZfn47pZLv4xEhYawvgcAAN4U1OUjJ5P5HgAAeFtQlo+1JVWSpAE86QIAgNcFXfkwDEOl1fWSpKykVianAQAg+ARd+bAdbVJDk1OSlBQbaXIaAACCT9CVj8ra5qse8VFhigoPNTkNAADBJ+jKR4XNLklKZkl1AABMEXTlo7K2uXy045YLAACmCL7yUXOsfMRRPgAAMEPQlY+KY+UjmfIBAIApgq58cOUDAABzUT4AAIBXBV35qKhpftQ2OY6nXQAAMEPQlQ+ufAAAYK6gKh8NTU4drmuURPkAAMAsQVU+Dhxb4yM81KLE6HCT0wAAEJyCqnx8d8slKTZSISEWk9MAABCcgrJ8cMsFAADzBFX5YIExAADMF1TlgysfAACYL7jKR23zGh9sKgcAgHmCqnxU2I5d+YhngTEAAMzisfLxyiuvKCsrS1FRURo8eLDy8vI89VYnrfLYo7Zc+QAAwDweKR/vvvuupkyZoieeeEKrV69W3759dfHFF6uiosITb3fSmPMBAID5PFI+XnzxRd15552aOHGievTooVdffVWtWrXSrFmzPPF2J8UwDJ52AQDAB7i9fDQ0NKigoECjR4/+75uEhGj06NFasWLFj8632+2y2WwtvjzBVt+khianJK58AABgJreXjwMHDsjhcCglJaXF8ZSUFJWVlf3o/OnTpyshIcH1ZbVa3R1J0n9vucRFhSkqPNQj7wEAAE7M9Kddpk6dqurqatdXSUmJR94nPipMv72wq+4Ynu2Rnw8AAE5OmLt/YFJSkkJDQ1VeXt7ieHl5uVJTU390fmRkpCIjPX8bJDk+SveO6uLx9wEAAD/P7Vc+IiIiNGDAAC1atMh1zOl0atGiRRoyZIi73w4AAPgZt1/5kKQpU6ZowoQJysnJ0aBBg/TSSy/pyJEjmjhxoifeDgAA+BGPlI8bb7xRlZWVevzxx1VWVqZ+/fpp4cKFP5qECgAAgo/FMAzD7BDfZ7PZlJCQoOrqasXHx5sdBwAAnIRT+fw2/WkXAAAQXCgfAADAqygfAADAqygfAADAqygfAADAqygfAADAqygfAADAqygfAADAqygfAADAqzyyvPqZ+G7BVZvNZnISAABwsr773D6ZhdN9rnzU1NRIkqxWq8lJAADAqaqpqVFCQsLPnuNze7s4nU7t379fcXFxslgsbv3ZNptNVqtVJSUl7BvjQYyzdzDO3sE4ew9j7R2eGmfDMFRTU6O0tDSFhPz8rA6fu/IREhKi9PR0j75HfHw8/7C9gHH2DsbZOxhn72GsvcMT43yiKx7fYcIpAADwKsoHAADwqqAqH5GRkXriiScUGRlpdpSAxjh7B+PsHYyz9zDW3uEL4+xzE04BAEBgC6orHwAAwHyUDwAA4FWUDwAA4FWUDwAA4FVBUz5eeeUVZWVlKSoqSoMHD1ZeXp7Zkfza9OnTNXDgQMXFxSk5OVljxozRtm3bWpxTX1+vSZMmqW3btoqNjdV1112n8vJykxIHhmeffVYWi0WTJ092HWOc3Wffvn265ZZb1LZtW0VHR6t3797Kz893vW4Yhh5//HG1b99e0dHRGj16tAoLC01M7H8cDocee+wxZWdnKzo6Wp06ddJTTz3VYj8QxvnULV26VFdeeaXS0tJksVg0f/78Fq+fzJgeOnRI48ePV3x8vBITE3XHHXeotrbWM4GNIDBv3jwjIiLCmDVrlrFp0ybjzjvvNBITE43y8nKzo/mtiy++2HjjjTeMjRs3GmvXrjUuu+wyIyMjw6itrXWdc/fddxtWq9VYtGiRkZ+fb5xzzjnG0KFDTUzt3/Ly8oysrCyjT58+xv333+86zji7x6FDh4zMzEzjtttuM3Jzc42ioiLjyy+/NHbs2OE659lnnzUSEhKM+fPnG+vWrTOuuuoqIzs72zh69KiJyf3LtGnTjLZt2xoLFiwwdu3aZbz//vtGbGys8ec//9l1DuN86j7//HPjkUceMT788ENDkvHRRx+1eP1kxvSSSy4x+vbta6xcudL49ttvjc6dOxvjxo3zSN6gKB+DBg0yJk2a5Pre4XAYaWlpxvTp001MFVgqKioMScaSJUsMwzCMqqoqIzw83Hj//fdd52zZssWQZKxYscKsmH6rpqbG6NKli/HVV18Z5513nqt8MM7u89BDDxnDhw//ydedTqeRmppqvPDCC65jVVVVRmRkpPHOO+94I2JAuPzyy43bb7+9xbFrr73WGD9+vGEYjLM7/LB8nMyYbt682ZBkrFq1ynXOF198YVgsFmPfvn1uzxjwt10aGhpUUFCg0aNHu46FhIRo9OjRWrFihYnJAkt1dbUkqU2bNpKkgoICNTY2thj3bt26KSMjg3E/DZMmTdLll1/eYjwlxtmdPvnkE+Xk5Gjs2LFKTk5W//799dprr7le37Vrl8rKylqMdUJCggYPHsxYn4KhQ4dq0aJF2r59uyRp3bp1WrZsmS699FJJjLMnnMyYrlixQomJicrJyXGdM3r0aIWEhCg3N9ftmXxuYzl3O3DggBwOh1JSUlocT0lJ0datW01KFVicTqcmT56sYcOGqVevXpKksrIyRUREKDExscW5KSkpKisrMyGl/5o3b55Wr16tVatW/eg1xtl9ioqKNGPGDE2ZMkW///3vtWrVKt13332KiIjQhAkTXON5vN8ljPXJe/jhh2Wz2dStWzeFhobK4XBo2rRpGj9+vCQxzh5wMmNaVlam5OTkFq+HhYWpTZs2Hhn3gC8f8LxJkyZp48aNWrZsmdlRAk5JSYnuv/9+ffXVV4qKijI7TkBzOp3KycnRM888I0nq37+/Nm7cqFdffVUTJkwwOV3geO+99zRnzhzNnTtXPXv21Nq1azV58mSlpaUxzkEk4G+7JCUlKTQ09Eez/8vLy5WammpSqsBxzz33aMGCBfr666+Vnp7uOp6amqqGhgZVVVW1OJ9xPzUFBQWqqKjQ2WefrbCwMIWFhWnJkiV6+eWXFRYWppSUFMbZTdq3b68ePXq0ONa9e3cVFxdLkms8+V1yZv7nf/5HDz/8sG666Sb17t1bt956qx544AFNnz5dEuPsCSczpqmpqaqoqGjxelNTkw4dOuSRcQ/48hEREaEBAwZo0aJFrmNOp1OLFi3SkCFDTEzm3wzD0D333KOPPvpIixcvVnZ2dovXBwwYoPDw8Bbjvm3bNhUXFzPup2DUqFHasGGD1q5d6/rKycnR+PHjXf+bcXaPYcOG/ehx8e3btyszM1OSlJ2drdTU1BZjbbPZlJuby1ifgrq6OoWEtPzoCQ0NldPplMQ4e8LJjOmQIUNUVVWlgoIC1zmLFy+W0+nU4MGD3R/K7VNYfdC8efOMyMhIY/bs2cbmzZuNu+66y0hMTDTKysrMjua3fv3rXxsJCQnGN998Y5SWlrq+6urqXOfcfffdRkZGhrF48WIjPz/fGDJkiDFkyBATUweG7z/tYhiMs7vk5eUZYWFhxrRp04zCwkJjzpw5RqtWrYy3337bdc6zzz5rJCYmGh9//LGxfv164+qrr+YR0FM0YcIEo0OHDq5HbT/88EMjKSnJePDBB13nMM6nrqamxlizZo2xZs0aQ5Lx4osvGmvWrDH27NljGMbJjekll1xi9O/f38jNzTWWLVtmdOnShUdtz9Rf/vIXIyMjw4iIiDAGDRpkrFy50uxIfk3Scb/eeOMN1zlHjx41fvOb3xitW7c2WrVqZVxzzTVGaWmpeaEDxA/LB+PsPp9++qnRq1cvIzIy0ujWrZsxc+bMFq87nU7jscceM1JSUozIyEhj1KhRxrZt20xK659sNptx//33GxkZGUZUVJTRsWNH45FHHjHsdrvrHMb51H399dfH/Z08YcIEwzBObkwPHjxojBs3zoiNjTXi4+ONiRMnGjU1NR7JazGM7y0rBwAA4GEBP+cDAAD4FsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwKsoHAADwqv8PXXhteuIF2t4AAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"xs = np.linspace(0, 100, num=200)\n",
|
||
"ys = np.sqrt(xs)\n",
|
||
"plt.plot(xs, ys)\n",
|
||
"plt.show()\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a98f7855-0bca-4769-aaf5-fa27f0404b23",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-998243908406c7d4",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Styling\n",
|
||
"\n",
|
||
"Da bei mehreren Plots der Überblick schnell verloren geht, beschäftigen wir uns im Folgenden mit dem **Styling**. Dabei werden wir im Schnelldurchlauf die wichtigsten Parameter und Möglichkeiten durchgehen, um Plots anschaulicher und übersichtlicher zu gestalten. \n",
|
||
"\n",
|
||
"Die Grundlage für alle folgenden Plots wird in der nächsten Zelle gesetzt, sodass wir ein konsistentes Layout und einheitliche Formatierungen verwenden können."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 32,
|
||
"id": "dd074404-20be-450e-a187-d992c9d804cf",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-a86ddac229c0bbbb",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"x = np.linspace(0, 2*np.pi, num=200)\n",
|
||
"s = np.sin(x)\n",
|
||
"c = np.cos(x)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "7e541a27-5fb0-48a5-98a6-175842a59f31",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-e27c575962048d7b",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Farbe ändern\n",
|
||
"\n",
|
||
"Die Standardfarbe für den ersten Plot ist immer Blau. Um die Farbe zu verändern, kann dem `plt.plot`-Aufruf der Parameter `color` übergeben werden. Dieser erwartet einen String, der die gewünschte Farbe definiert. \n",
|
||
"\n",
|
||
"Für eine detaillierte Erläuterung siehe die Dokumentation zu [Specifying color](https://matplotlib.org/stable/users/explain/colors/colors.html). \n",
|
||
"\n",
|
||
"In diesem Notebook werden die Beispiele vorwiegend mit den sogenannten \"Single Character Shorthands\" aus der Dokumentation versehen. \n",
|
||
"\n",
|
||
"Plotten wir den Sinus nun in Rot:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 33,
|
||
"id": "01d03aa6-22c3-4843-8cf0-33155b78740e",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-1ec79feac73af81f",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAT3pJREFUeJzt3Xt8zvX/x/HHNrYhG8JmNaeUQwmRtdS3vtnXHL7F99uBoiGHaIjJYeVQKZQOIjmfOjhUvwiV0nLoIEQrhBI5xCZhF5Nhu35/vL/bLKeNXXtfh+f9dvvcrveufa7Pntei6+X9eR/8nE6nExEREREv4m87gIiIiEhhU4EjIiIiXkcFjoiIiHgdFTgiIiLidVTgiIiIiNdRgSMiIiJeRwWOiIiIeB0VOCIiIuJ1itkOYENWVhb79u2jdOnS+Pn52Y4jIiIi+eB0Ojl69CgRERH4+1+4j8YnC5x9+/YRGRlpO4aIiIhcgj179nD11Vdf8ByfLHBKly4NmF9QSEiI5TQiIiKSHw6Hg8jIyJzP8QvxyQIn+7ZUSEiIChwREREPk5/hJRpkLCIiIl5HBY6IiIh4HRU4IiIi4nVU4IiIiIjXUYEjIiIiXkcFjoiIiHgdFTgiIiLidVTgiIiIiNdRgSMiIiJex6UFzqpVq7j77ruJiIjAz8+PhQsXXvQ1K1as4KabbiIoKIgaNWowa9ass86ZMGECVatWJTg4mKioKNauXVv44UVERMRjubTASU9Pp169ekyYMCFf5+/cuZNWrVrxz3/+k+TkZPr27UvXrl359NNPc86ZP38+CQkJDB8+nA0bNlCvXj1iY2M5cOCAq96GiIiIeBg/p9PpLJIf5OfHggULaNOmzXnPGTRoEB999BGbNm3Kea5du3YcOXKEpUuXAhAVFcXNN9/M66+/DkBWVhaRkZH07t2bwYMH5yuLw+EgNDSUtLQ07UUlIiLiIQry+e1Wm22uXr2amJiYPM/FxsbSt29fAE6ePMn69etJTEzM+b6/vz8xMTGsXr36vNfNyMggIyMj52uHw1G4wcUznTgBP/9sjpQUOHDAPHfqFAQGQkgIXHklVK0K1avDNddAQIDt1CIikg9uVeCkpKQQFhaW57mwsDAcDgd//fUXhw8fJjMz85znbN269bzXHTVqFM8884xLMosHOXYMPv0Uli+HL7+ETZsgKyv/r7/iCrjpJrj9doiNhVtugeLFXZdXREQumVsVOK6SmJhIQkJCztcOh4PIyEiLiaTIZGTAhx/CW2/BsmXm6zOFhkLt2nDVVRAWBiVLQrFicPIkOBymV2fnTti+3RRIq1aZ4/nnoVw5uO8+aN/eFD1+fnbeo4iInMWtCpzw8HBSU1PzPJeamkpISAglSpQgICCAgICAc54THh5+3usGBQURFBTkkszipvbvh9deg2nT4M8/c5+vUQNatDAFSXS0KWzyU5hkZsLWrbBmDXz+uSmWDh6EKVPMUacOxMdDx45QqpTr3peIiOSLW62DEx0dTVJSUp7nli1bRnR0NACBgYE0bNgwzzlZWVkkJSXlnCM+bu9eePRRM27mhRdMcXPVVfDkk+aW1M8/w7hxcP/9cPXV+e91CQiA66+HRx6BOXPMmJ2kJOjSxdy6+uknU+BUqwZjxpjeHhERscalBc6xY8dITk4mOTkZMNPAk5OT2b17N2BuHcXFxeWc36NHD3bs2MHAgQPZunUrb7zxBu+++y79+vXLOSchIYGpU6cye/ZstmzZQs+ePUlPT6dz586ufCvi7hwOGDgQrr3W9KicPAlNmsCCBbBrl7mldP31hXcbKSAA7rrL9BDt3WuKpmrV4I8/cnPMnFmwMT4iIlJ4nC60fPlyJ3DW0bFjR6fT6XR27NjReccdd5z1mvr16zsDAwOd1atXd86cOfOs644fP95ZuXJlZ2BgoLNx48bOb7/9tkC50tLSnIAzLS3tEt+ZuI2sLKfznXeczvBwpxPMcfvtTueqVUWf5eRJp3PmTKezWrXcLDfd5HSuX1/0WUREvFBBPr+LbB0cd6J1cLzE779Dt27wySfm6xo1YOxYaNnS7oDfjAwYPx5GjDA9SwEB0K8fPPsslChhL5eIiIcryOe3W43BEcm3uXPNLadPPoGgIFNMbNoErVrZn80UFARPPGHG+7RtawYov/QS3Hwz/PCD3WwiIj5CBY54luPHoWtXeOghSEszRcOGDTBkiCks3ElYGMybB4sWmfbmzdC4Mbz+urmBJSIiLqMCRzzHjh0QFQXTp5temqFD4ZtvzBRtd3b33fDjj+bx5Eno3RsefhjS020nExHxWipwxDMkJZnemk2bTG/I55+bMS3F3Gopp/OrWNEsOPjKK2ZMzjvvwK23wv9mFIqISOFSgSPub9o0szXCoUPmFs+GDWaKtqfx8zODjb/4whRpP/5oeqTWrbOdTETE66jAEffldMLw4WamVGamua2zciVERNhOdnn+8Q+zInLdumbBwDvugI8+sp1KRMSrqMAR95SZaVYkfvZZ8/WwYTB7NgQH281VWKpUga++MttG/PUXtG5t9ssSEZFCoQJH3M+pUxAXB1Ongr+/WZn4mWfsT/8ubCEhZlxOhw6moIuLg0mTbKcSEfEKKnDEvZw6Be3amf2eihUz06y7dbOdynWKFzc9U48/br7u2dOMORIRkcviIVNQxCdkZkKnTvDBB2ZNm//7P7Nwn7fz94dXXzU9VGPHQvfuprjr1Ml2MhERj6UeHHEPTqfpvcjuuXn/fd8obrL5+Zkp5L16md/FI4/A22/bTiUi4rFU4Ih9Tif075875ubtt+Hf/7adquj5+ZldyXv0ML+Tjh3NLToRESkwFThi39NPm1s0YMaftG1rNY5Vfn4wYYLZjiIry0yN//xz26lERDyOChyx6403cqeCjxsHnTvbzeMO/P1h8mR48EE4fRruvdes4CwiIvmmAkfs+fRT6NPHtEeMMHs0ieHvDzNnwu23g8MBLVvCvn22U4mIeAwVOGLH5s3wwANm5lTHjvDUU7YTuZ+gIFi4EGrWhD17zLikY8dspxIR8QgqcKToHThgPqwdDrNtwZQp3reIX2EpVw4+/hgqVIDvvzfjk06ftp1KRMTtqcCRonXiBLRpA7/9BtdcY9a8CQy0ncq9Va8OS5ZAiRKm2BkwwHYiERG3pwJHio7TaVYlXr0aypQxG0xeeaXtVJ6hcePcdXHGjtX0cRGRi1CBI0Vn4kTzIR0QYBbyq1nTdiLP8t//QmKiaXfpoplVIiIXoAJHisbatdC3r2m/+CI0bWo1jscaMQJiYuD4cVPwpKXZTiQi4pZU4Ijr/fkn3H+/2UjzP/+Bfv1sJ/JcAQEwdy5Urgy//GJmoGVl2U4lIuJ2VOCIa2VlQVwc7N5tBhXPnKkZU5erfHmzEWlQEHz4IYwebTuRiIjbUYEjrjV6tJn5Exxsxt2EhtpO5B0aNTJbOgAMHQpffmk3j4iIm1GBI66zcqX58AXzYVy/vtU4XqdLl9xbVB06wJEjthOJiLgNFTjiGkeOmI0is7LMh/Ajj9hO5J3Gjze3/nbvzt2FXEREVOCIi8THm+0FrrkGXn/ddhrvVbo0zJkDxYrB/Pnw5pu2E4mIuAUVOFL45s41H7oBAWbdmyuusJ3IuzVuDM88Y9rx8bB9u908IiJuQAWOFK49e6BnT9MeMgRuucVuHl8xaBDccQekp8NDD5kp+SIiPkwFjhSe7PE2aWkQFaUdwotSQAC89ZbZAmPdOrMgoIiID1OBI4Xn1Vdh+XIoWdJ82BYvbjuRb4mMhMmTTXvkSLP7uIiIjyqSAmfChAlUrVqV4OBgoqKiWLt27XnPvfPOO/Hz8zvraNWqVc45nTp1Ouv7zZs3L4q3IuezdWtuj83YsXDttVbj+KwHHoD77oPMTOjcGU6etJ1IRMQKlxc48+fPJyEhgeHDh7Nhwwbq1atHbGwsBw4cOOf5H3zwAfv37885Nm3aREBAAPfff3+e85o3b57nvLlz57r6rcj5ZGVB166QkQHNm5u22DNhgtml/YcftMqxiPgslxc4r7zyCt26daNz587UqVOHSZMmUbJkSWbMmHHO88uVK0d4eHjOsWzZMkqWLHlWgRMUFJTnvLJly7r6rcj5vPEGfP21mS01ebK2YrCtYkWzPg6YsTg//mg3j4iIBS4tcE6ePMn69euJiYnJ/YH+/sTExLB69ep8XWP69Om0a9eOUqVK5Xl+xYoVVKxYkZo1a9KzZ0/+/PPP814jIyMDh8OR55BCsmsXDB5s2i+8YDaBFPvatYPWreH0aXOrSrOqRMTHuLTAOXjwIJmZmYSFheV5PiwsjJSUlIu+fu3atWzatImuf7vl0bx5c958802SkpJ44YUXWLlyJS1atCAzM/Oc1xk1ahShoaE5R2Rk5KW/KcnldMKjj5qpybfdZlbSFffg5wcTJ0LZsrBhA4wZYzuRiEiRcutZVNOnT6du3bo0btw4z/Pt2rXjnnvuoW7durRp04YlS5awbt06VqxYcc7rJCYmkpaWlnPs2bOnCNL7gDffhE8/NbtaT5sG/m79x8n3VKoEr71m2s88A9u22c0jIlKEXPqJVL58eQICAkhNTc3zfGpqKuHh4Rd8bXp6OvPmzaNLly4X/TnVq1enfPnybD/PCq5BQUGEhITkOeQypaRAv36m/fTTULOm1ThyHh06QIsWZjbVY49pryoR8RkuLXACAwNp2LAhSUlJOc9lZWWRlJREdHT0BV/73nvvkZGRQYcOHS76c/bu3cuff/5JpUqVLjuz5FNCAhw+DA0aQP/+ttPI+fj5mb3AgoPhiy/MFhoiIj7A5fcUEhISmDp1KrNnz2bLli307NmT9PR0OnfuDEBcXByJiYlnvW769Om0adOGK6+8Ms/zx44dY8CAAXz77bf89ttvJCUl0bp1a2rUqEFsbKyr346A+aCcO9d8eE6dqgX93F316jB0qGlnF6YiIl6umKt/QNu2bfnjjz8YNmwYKSkp1K9fn6VLl+YMPN69ezf+fxu7sW3bNr766is+++yzs64XEBDAjz/+yOzZszly5AgRERE0a9aMESNGEBQU5Oq3IydPmg0dwew51bCh3TySP088YTY+3bIFnnzSDEAWEfFifk6n792UdzgchIaGkpaWpvE4BfXCC2ZaeIUKZtCq1h/yHCtXwp13mp63b77RRqgi4nEK8vmtaS+Sf7t3w7PPmvZLL6m48TR33AFxcWagcY8eZo0cEREvpQJH8q9vXzh+HG6/HR5+2HYauRRjxpjC9IcfzOBjEREvpQJH8ueTT2DBAggIMHsdaTsGz1SxYu7+VE8/DefZE05ExNOpwJGLy8iA3r1N+/HHoW5du3nk8nTpAjfdBGlpMGSI7TQiIi6hAkcu7rXX4Ndfzcq4Tz9tO41croCA3BWOp02D77+3m0dExAVU4MiFpabCc8+Z9qhRULq03TxSOG67zWzI6XRCnz5a4VhEvI4KHLmwIUPg6FFo1EgDi73Niy9CiRLw1Vfw7ru204iIFCoVOHJ+yckwfbppjx2rzTS9TWSkWdMIYMAAM0NORMRL6BNLzs3pNNPCnU5o2xaaNLGdSFxhwACoXBn27DE9OiIiXkIFjpzbwoVm5dvgYLN6sXinEiXMoo1g/jvv2WM3j4hIIVGBI2fLyDB7F4F5rFLFbh5xrfvuM4s3njiRuymniIiHU4EjZxs3DnbsMNPCBw2ynUZczc8vtxfnzTfNKsciIh5OBY7kdegQjBxp2iNHwhVX2M0jRaNxYzPWyumEgQNtpxERuWwqcCSvUaPgyBGzWrGmhfuWkSOheHH47DNziIh4MBU4kmv3bhg/3rRHjzYr3orvqF4d4uNNe+BAyMy0m0dE5DKowJFcQ4eaAcZ33gktWthOIzYMGQKhoWYczttv204jInLJVOCI8cMP8NZbpv3ii9ot3FddeSU8+aRpDxkCf/1lN4+IyCVSgSNGYqIZYPrAA3DzzbbTiE19+pjF//buzd2UU0TEw6jAEVi+HD75BIoVg+eft51GbAsOzt1g9YUX4PBhu3lERC6BChxfd+a04B49oEYNu3nEPTz0ENxwg5lRl71GjoiIB1GB4+sWLIDvvjPr3WgVW8kWEJDbizN2LKSmWo0jIlJQKnB8WWZmblHTrx9UrGg3j7iXe+4xCwAeP567+KOIiIdQgePL5s2Dn36CMmUgIcF2GnE3fn65Y7ImTTLrJImIeAgVOL7q1CkYPty0Bw40RY7I3zVtCv/8J5w8Cc8+azuNiEi+qcDxVbNnw6+/mttSffrYTiPu6sxenFmzYNs2q3FERPJLBY4vysjI/dd4YiKUKmU3j7i36Gi4+24zZiu7109ExM2pwPFFU6bAnj1w1VVmarjIxWTPqJo/36x6LSLi5lTg+Jrjx3NvOQwdahZ1E7mYG2+Etm1N+5ln7GYREckHFTi+ZsIEs6ZJ9erwyCO204gnGTbMjMlZsACSk22nERG5IBU4vuTYMbORJpgPq+LF7eYRz1KnjnpxRMRjqMDxJRMnwsGDZjuG9u1tpxFPlN2Ls3AhfP+97TQiIudVJAXOhAkTqFq1KsHBwURFRbF27drznjtr1iz8/PzyHMF/GyfidDoZNmwYlSpVokSJEsTExPDLL7+4+m14tvR0GDPGtIcMMRtrihRU7drQrp1pqxdHRNyYywuc+fPnk5CQwPDhw9mwYQP16tUjNjaWAwcOnPc1ISEh7N+/P+fYtWtXnu+/+OKLjBs3jkmTJrFmzRpKlSpFbGwsJ06ccPXb8VyTJsEff8A116j3Ri5Pdi/Ohx+qF0dE3JbLC5xXXnmFbt260blzZ+rUqcOkSZMoWbIkM2bMOO9r/Pz8CA8PzznCwsJyvud0Ohk7dixDhgyhdevW3Hjjjbz55pvs27ePhQsXuvrteKbjx3PH3jz1lHpv5PLUqgUPPmjaTz9tNYqIyPm4tMA5efIk69evJyYmJvcH+vsTExPD6tWrz/u6Y8eOUaVKFSIjI2ndujWbN2/O+d7OnTtJSUnJc83Q0FCioqLOe82MjAwcDkeew6dMmgQHDkC1atChg+004g2GDgV/f1i0CDZssJ1GROQsLi1wDh48SGZmZp4eGICwsDBSUlLO+ZqaNWsyY8YMPvzwQ95++22ysrK49dZb2bt3L0DO6wpyzVGjRhEaGppzREZGXu5b8xxn9t4MGaKZU1I4zuzF0VgcEXFDbjeLKjo6mri4OOrXr88dd9zBBx98QIUKFZg8efIlXzMxMZG0tLScY8+ePYWY2M1NmWLWvalWDR5+2HYa8SZDh5qxOIsWwcaNttOIiOTh0gKnfPnyBAQEkJqamuf51NRUwsPD83WN4sWL06BBA7Zv3w6Q87qCXDMoKIiQkJA8h0/46y944QXTfvJJ9d5I4apZE+6/37RHjrSbRUTkb1xa4AQGBtKwYUOSkpJynsvKyiIpKYno6Oh8XSMzM5ONGzdSqVIlAKpVq0Z4eHieazocDtasWZPva/qMmTMhJQWqVIG4ONtpxBs9+aR5fPdd0FINIuJGXH6LKiEhgalTpzJ79my2bNlCz549SU9Pp3PnzgDExcWRmJiYc/6zzz7LZ599xo4dO9iwYQMdOnRg165ddO3aFTAzrPr27ctzzz3HokWL2LhxI3FxcURERNCmTRtXvx3PcepU7tibgQMhMNBuHvFO9erBv/8NWVkwerTtNCIiOVw+X7ht27b88ccfDBs2jJSUFOrXr8/SpUtzBgnv3r0bf//cOuvw4cN069aNlJQUypYtS8OGDfnmm2+oU6dOzjkDBw4kPT2d7t27c+TIEW677TaWLl161oKAPm3uXNi1C8LC4H/FpIhLPPUULFkCb74Jw4dD5cq2E4mI4Od0Op22QxQ1h8NBaGgoaWlp3jkeJysLrr8etm41Y3AGDrSdSLzdXXfB8uXQqxeMH287jYh4qYJ8frvdLCopBAsXmuKmTBno0cN2GvEFTz1lHqdNM7P2REQsU4HjbZzO3BktvXuDN/ZQifu56y6IioITJ+CVV2ynERFRgeN1li2D9euhZEno08d2GvEVfn65vThvvAGHDtnNIyI+TwWOt8nuvXn0UShf3m4W8S3//jfceCMcO6ZxOCJinQocb/L117BypVnQr39/22nE1/j55a6L89prcPSo3Twi4tNU4HiTUaPMY6dOcNVVVqOIj7rvPrjuOjh8GC5jexURkculAsdbJCfDRx+ZHZ41LVxsCQiAwYNN++WXzaBjERELVOB4i+xVZB94AGrUsJtFfFuHDmaxv5QUmDHDdhoR8VEqcLzBzz+bvYAAztj2QsSK4sVzexFffhlOn7abR0R8kgocb/Dii2b9m+xZLCK2de4MV14JO3bABx/YTiMiPkgFjqf7/XezBxCo90bcR8mSZqFJyC3ARUSKkAocTzdunNk5/Pbb4dZbbacRyRUfDyVKmIUnV6ywnUZEfIwKHE/mcMCkSaY9YIDdLCJ/V748PPKIab/4ot0sIuJzVOB4sqlTTZFTqxa0amU7jcjZEhLM0gVLl8KPP9pOIyI+RAWOpzp1CsaONe0nnjAfIiLupnp1uP9+0x4zxm4WEfEp+lT0VPPmwd69EB5u1h0RcVfZt0/nzYPdu+1mERGfoQLHEzmduf8a7tMHgoLs5hG5kIYN4a67zHo42b2OIiIupgLHE332GWzcCKVKQY8ettOIXFz2wn9Tpph9qkREXEwFjifK7r3p1g3KlrWbRSQ/mjUzi1Cmp8PEibbTiIgPUIHjaTZsgKQks6lh376204jkj59f7licceO0CaeIuJwKHE/z0kvmsW1bqFLFbhaRgmjbFiIjITUV3nrLdhoR8XIqcDzJrl25m2pqYT/xNMWLm3VxwBTqmZl284iIV1OB40lefdV8KMTEQP36ttOIFFzXrlCmDPz8MyxaZDuNiHgxFTie4vBhmDbNtNV7I57qiiugZ0/TfvVVu1lExKupwPEUEyeaGSj16sG//mU7jcil69XL3K768ktYt852GhHxUipwPEFGBowfb9pPPGFmpIh4qogIaNfOtNWLIyIuogLHE8yfDykpcNVVZiaKiKfr1888vvsu7NljN4uIeCUVOO7O6cz9V252176Ip2vQAP75TzNoPrt3UkSkEKnAcXcrV0JyMpQoAd27204jUniyp4xPmQJHj9rNIiJeRwWOu8vuvenYEcqVs5tFpDC1bAnXXQdpaTBzpu00IuJlVOC4s+3bYfFi09a2DOJt/P1zx+KMHauF/0SkUBVJgTNhwgSqVq1KcHAwUVFRrF279rznTp06ldtvv52yZctStmxZYmJizjq/U6dO+Pn55TmaN2/u6rdR9F57zYzBadkSata0nUak8MXFmZ7JnTvhww9tpxERL+LyAmf+/PkkJCQwfPhwNmzYQL169YiNjeXAgQPnPH/FihU8+OCDLF++nNWrVxMZGUmzZs34/fff85zXvHlz9u/fn3PMnTvX1W+laB05ktttn/2vXBFvU7Jk7sJ/r7xiN4uIeBU/p9PpdOUPiIqK4uabb+b1118HICsri8jISHr37s3gwYMv+vrMzEzKli3L66+/TlxcHGB6cI4cOcLChQsvKZPD4SA0NJS0tDRCQkIu6RouN2YMDBwIdevCDz9o7RvxXvv3m41jT52Cb7+FqCjbiUTETRXk89ulPTgnT55k/fr1xMTE5P5Af39iYmJYvXp1vq5x/PhxTp06Rbm/DbBdsWIFFStWpGbNmvTs2ZM///zzvNfIyMjA4XDkOdza6dO5U2f79lVxI96tUiV48EHT1sJ/IlJIXFrgHDx4kMzMTMLCwvI8HxYWRkpKSr6uMWjQICIiIvIUSc2bN+fNN98kKSmJF154gZUrV9KiRQsyzzNIcdSoUYSGhuYckZGRl/6misL//Z9Z/KxiRXjoIdtpRFwv+zbs++/Drl12s4iIV3DrWVSjR49m3rx5LFiwgODg4Jzn27Vrxz333EPdunVp06YNS5YsYd26daxYseKc10lMTCQtLS3n2OPuK6dm/yu2Z084432LeK369eGuu7Twn4gUGpcWOOXLlycgIIDU1NQ8z6emphIeHn7B17700kuMHj2azz77jBtvvPGC51avXp3y5cuzffv2c34/KCiIkJCQPIfbWr0a1qyBwMDcwZciviB74b+pU8HdbyOLiNtzaYETGBhIw4YNSUpKynkuKyuLpKQkoqOjz/u6F198kREjRrB06VIaNWp00Z+zd+9e/vzzTypVqlQoua3K7r1p3x7+dmtPxKu1aGGWQ3A4YNYs22lExMO5/BZVQkICU6dOZfbs2WzZsoWePXuSnp5O586dAYiLiyMxMTHn/BdeeIGhQ4cyY8YMqlatSkpKCikpKRw7dgyAY8eOMWDAAL799lt+++03kpKSaN26NTVq1CA2NtbVb8e1du0y429AU8PF9/j7Q58+pj1+PGRl2c0jIh7N5QVO27Zteemllxg2bBj169cnOTmZpUuX5gw83r17N/v37885f+LEiZw8eZL77ruPSpUq5RwvvfQSAAEBAfz444/cc889XHfddXTp0oWGDRvy5ZdfEhQU5Oq341rZ/1Nv2tRMDxfxNXFxEBpqVvH++GPbaUTEg7l8HRx35Jbr4Bw9CldfbbrnlyyBVq1sJxKx44kn4OWXISYGli2znUZE3IjbrIMjBTBzpiluatY0YxFEfFWvXuZ21eefw+bNttOIiIdSgeMOMjPNvlMAjz9u/ucu4quqVoXWrU173DirUUTEc+mT1B0sXgw7dkDZsmYMgoive/xx8/jWW3DokN0sIuKRVOC4g+yp4Y8+CqVK2c0i4g7+8Q+z+N9ff5l1cURECkgFjm3JybBqFQQEQHy87TQi7sHPL7cXZ8IEsz+biEgBqMCxLXtZ+vvuM7OoRMRo1w4qVDD7si1YYDuNiHgYFTg2HTwI77xj2tkLnImIERwMPXqY9tixVqOIiOdRgWPT1KmQkQENG8IFtq4Q8Vk9e0Lx4vDNN/Ddd7bTiIgHUYFjy6lT8MYbpt2njxlzICJ5VaoEDzxg2tlLKYiI5IMKHFsWLoS9e6FiRWjb1nYaEfeVPdh4/nw4Y1sXEZELUYFjS/YCZo8+Cp6+h5aIK918s7mFe+oUTJpkO42IeAgVODZs2ABffQXFiuUOohSR8+vb1zxOmmTGrYmIXIQKHBuyp4bffz9ERNjNIuIJ/vMfs4zCgQMwb57tNCLiAVTgFLUDB2DOHNPW1HCR/ClePHchzNdeA6fTbh4RcXsqcIra1Klw8qQZVxAVZTuNiOfo1g1KlIDvvze3eEVELkAFTlHS1HCRS3flldChg2lryriIXIQKnKL0wQewbx+EhZnxNyJSMNm3dRcsgF277GYREbemAqcoZU8N79FDU8NFLsUNN0DTppCVldsbKiJyDipwisp335nl5osXN2vfiMilyV74b+pUOH7cbhYRcVsqcIpK9tTwBx4wy8+LyKVp2RKqV4fDh3M3qxUR+RsVOEUhNTV37Q5NDRe5PAEB0KuXaY8bpynjInJOKnCKwpQpZmp4VBQ0bmw7jYjn69wZSpWCTZtgxQrbaUTEDanAcbWTJ2HiRNNW741I4ShTBjp2NG1NGReRc1CB42r/939mB+TwcLjvPttpRLxH9m2qRYtg5067WUTE7ajAcbXsqeE9e0JgoN0sIt6kdm1o1syMwZkwwXYaEXEzKnBcae1a+PZbTQ0XcZXs277TpsGxY3aziIhbUYHjStlTw9u1M6sXi0jhatECatSAtDR4+23baUTEjajAcZWUFJg/37R797abRcRb+fvn/v3SlHEROYMKHFeZPNlsrhkdbXYOFxHX6NQJrrgCtmyBpCTbaUTETajAcQVNDRcpOiEhZl0cyB3ULyI+TwWOK7z3nlm9OCIC7r3XdhoR75c9ZXzJEvj1V7tZRMQtFEmBM2HCBKpWrUpwcDBRUVGsXbv2gue/99571KpVi+DgYOrWrcvHH3+c5/tOp5Nhw4ZRqVIlSpQoQUxMDL/88osr30LBnDk1vHhxu1lEfMF115kBx04nvP667TQi4gZcXuDMnz+fhIQEhg8fzoYNG6hXrx6xsbEcOHDgnOd/8803PPjgg3Tp0oXvv/+eNm3a0KZNGzZt2pRzzosvvsi4ceOYNGkSa9asoVSpUsTGxnLixAlXv52LW7PGTA8PDITu3W2nEfEd2beDZ8yAo0ftZhER+5wu1rhxY2d8fHzO15mZmc6IiAjnqFGjznn+Aw884GzVqlWe56KiopyPPvqo0+l0OrOyspzh4eHOMWPG5Hz/yJEjzqCgIOfcuXPzlSktLc0JONPS0gr6di7uoYecTnA6O3Ys/GuLyPllZjqd111n/v69/rrtNCLiAgX5/HZpD87JkydZv349MTExOc/5+/sTExPD6tWrz/ma1atX5zkfIDY2Nuf8nTt3kpKSkuec0NBQoqKiznvNjIwMHA5HnsMl9u2Dd981bU0NFyla/v65vTjjx0NWlt08Ir5q82b4739h5UqrMVxa4Bw8eJDMzEzC/rbIXVhYGCkpKed8TUpKygXPz34syDVHjRpFaGhozhEZGXlJ7+eiJk+G06ehSRNo2NA1P0NEzi8uzsyq2rYNli2znUbEN40fDwsW5C52a4lPzKJKTEwkLS0t59izZ49rflDHjpCQAAMGuOb6InJhpUvDI4+YtqaMixS9w4fhrbdM2/KdDJcWOOXLlycgIIDU1NQ8z6emphIeHn7O14SHh1/w/OzHglwzKCiIkJCQPIdLVK8OL78MrVu75voicnHx8eDnBx9/DD//bDuNiG+ZMQOOH4cbb4R//MNqFJcWOIGBgTRs2JCkM1YXzcrKIikpiejo6HO+Jjo6Os/5AMuWLcs5v1q1aoSHh+c5x+FwsGbNmvNeU0R8SI0a0KqVaWvKuEjRyczM/TvXp4/5h4ZFLr9FlZCQwNSpU5k9ezZbtmyhZ8+epKen0/l/K4/GxcWRmJiYc/7jjz/O0qVLefnll9m6dStPP/003333Hb3+t5CXn58fffv25bnnnmPRokVs3LiRuLg4IiIiaNOmjavfjoh4guzBxjNngqsmFYhIXkuWwG+/Qbly8NBDttNQzNU/oG3btvzxxx8MGzaMlJQU6tevz9KlS3MGCe/evRt//9w669Zbb2XOnDkMGTKEJ598kmuvvZaFCxdyww035JwzcOBA0tPT6d69O0eOHOG2225j6dKlBAcHu/rtiIgniImB2rXN/lSzZmnLFJGikD2ouFs3KFHCbhbAz+n0ve13HQ4HoaGhpKWluW48jojYNXEiPPaYuWW1bZuZRi4irrF5M9xwg/l7tnMnVK7skh9TkM9v/Y0XEe8UFwehobB9OyxdajuNiHfL7r1p08ZlxU1BqcAREe9UqhR07WramjIu4jpnTg13o9vBKnBExHtlTxn/9FPYutV2GhHvlD01vG5d61PDz6QCR0S8V7VqcM89pm15VVURr+RmU8PPpAJHRLxbdpf57Nlw5IjVKCJe56OP3Gpq+JlU4IiId/vnP+H66yE93ayLIyKFJ3t8W9euULKk3Sx/owJHRLybn19uL87rr5sudRG5fJs3Q1KSmRr+2GO205xFBY6IeL/27aFsWdixw+xRJSKXL3vsTZs2UKWK1SjnogJHRLyfpoyLFK7Dh+HNN03b8q7h56MCR0R8Q3y86Ur//HP46SfbaUQ828yZuVPD77jDdppzUoEjIr6hShXTlQ7qxRG5HGdODe/d262mhp9JBY6I+I7swcZvvmm62EWk4D76yOw3VbasGd/mplTgiIjv+Mc/4MYb4a+/YPp022lEPNOZu4a72dTwM6nAERHfoSnjIpfnp5/MODY3nRp+JhU4IuJbHnrIrLq6axcsXmw7jYhnye69ad3aLaeGn0kFjoj4lhIloHt309ZgY5H8O3TIbHkCbrVr+PmowBER3/PYYxAQAMuXw8aNttOIeIZp08z4tXr13HZq+JlU4IiI74mMhP/+17TViyNycadP504Nf/xxt50afiYVOCLim7K72N9+G/78024WEXe3YAHs2QMVKsCDD9pOky8qcETENzVpAg0awIkTputdRM7vtdfMY48eEBxsN0s+qcAREd905pTxCRNMF7yInO277+Drr6F4cejZ03aafFOBIyK+q107KF/edL1/+KHtNCLuKbv3pm1bqFTJbpYCUIEjIr4rOBgefdS0NdhY5Gz798P8+ab9+ON2sxSQChwR8W09e5op46tWQXKy7TQi7mXiRDh1Cm69FRo1sp2mQFTgiIhvu+oquO8+085epVVEzAD8SZNMu29fq1EuhQocEZHsrvd33oE//rCbRcRdzJ1r/j5ERsJ//mM7TYGpwBERueUW0/2ekQFTp9pOI2Kf05k7uLhXLyhWzG6eS6ACR0TkzCnjb7xhxhyI+LJVq+CHH8zebV272k5zSVTgiIgAPPAAVKwIv/9uVm0V8WVjx5rHuDgoV85qlEulAkdEBCAoyKzSCpoyLr5tx47cdaE8YNfw81GBIyKSrUcPM9bg669h/XrbaUTseP11MwanWTOoU8d2mkvm0gLn0KFDtG/fnpCQEMqUKUOXLl04duzYBc/v3bs3NWvWpESJElSuXJk+ffqQlpaW5zw/P7+zjnnz5rnyrYiIL6hUydyqAk0ZF9909ChMn27aHjg1/EwuLXDat2/P5s2bWbZsGUuWLGHVqlV07979vOfv27ePffv28dJLL7Fp0yZmzZrF0qVL6dKly1nnzpw5k/379+ccbdq0ceE7ERGfkd0lP3cupKbazSJS1GbNAocDrrsOYmNtp7ksfk6n0+mKC2/ZsoU6deqwbt06Gv1v9cOlS5fSsmVL9u7dS0RERL6u895779GhQwfS09Mp9r9pan5+fixYsOCSixqHw0FoaChpaWmEhIRc0jVExIvdcgusWQPDhsEzz9hOI1I0srKgVi345Rdzmyo+3naisxTk89tlPTirV6+mTJkyOcUNQExMDP7+/qxZsybf18l+E8X+Ngc/Pj6e8uXL07hxY2bMmMGF6rSMjAwcDkeeQ0TkvBISzOMbb8Bff9nNIlJUPvnEFDehodCxo+00l81lBU5KSgoVK1bM81yxYsUoV64cKSkp+brGwYMHGTFixFm3tZ599lneffddli1bxr333stjjz3G+AvcLx81ahShoaE5R2RkZMHfkIj4jv/+FypXhoMH4e23bacRKRqvvmoeu3aFK66wm6UQFLjAGTx48DkH+Z55bN269bKDORwOWrVqRZ06dXj66afzfG/o0KE0adKEBg0aMGjQIAYOHMiYMWPOe63ExETS0tJyjj179lx2PhHxYsWK5W7f8OqrputexJslJ0NSktl4tndv22kKRYHXXu7fvz+dOnW64DnVq1cnPDycAwcO5Hn+9OnTHDp0iPDw8Au+/ujRozRv3pzSpUuzYMECihcvfsHzo6KiGDFiBBkZGQQFBZ31/aCgoHM+LyJyXl26wNNPw5Yt8Omn0KKF7UQirpPde3PffVClit0shaTABU6FChWoUKHCRc+Ljo7myJEjrF+/noYNGwLwxRdfkJWVRVRU1Hlf53A4iI2NJSgoiEWLFhEcHHzRn5WcnEzZsmVVxIhI4QkNNV31r75qDhU44q327TOzBiF3/JkXcNkYnNq1a9O8eXO6devG2rVr+frrr+nVqxft2rXLmUH1+++/U6tWLdauXQuY4qZZs2akp6czffp0HA4HKSkppKSkkJmZCcDixYuZNm0amzZtYvv27UycOJGRI0fS20u61ETEjfTpA/7+sGwZbNxoO42Ia7z+utl/7bbboHFj22kKjUu3B33nnXfo1asXTZs2xd/fn3vvvZdxZyyBfurUKbZt28bx48cB2LBhQ84Mqxo1auS51s6dO6latSrFixdnwoQJ9OvXD6fTSY0aNXjllVfo1q2bK9+KiPiiqlXh3nvhvfdML86MGbYTiRSu9HSYNMm0+/e3m6WQuWwdHHemdXBEJN++/RaioyEwEHbtgouMIRTxKBMmQK9ecM01sG2bGWTsxtxiHRwREa9wyy2mwDl50qyLI+ItMjNzBxf36+f2xU1BqcAREbkYLfwn3mjxYvj1VyhbFi4yO9oTqcAREbmYNm3MeJw//4S33rKdRqRwvPyyeezRA0qVspvFBVTgiIhcjBb+E2+zdi189RUUL27G4HghFTgiIvnxyCMQEgJbt8LSpbbTiFyeV14xjw8+CPnc/NrTqMAREcmPkBDIXo4iu2tfxBPt2gXvv2/aXrSw39+pwBERya8+fcxMky++gA0bbKcRuTTjxpkZVE2bQr16ttO4jAocEZH8qlwZ2rY17Qts8CvithwOmDrVtL1sYb+/U4EjIlIQAwaYx3ffhZ077WYRKaipU+HoUahdG2JjbadxKRU4IiIFUb8+NGtmZlJlL5Im4glOnsz9M9u/v9lnzYt597sTEXGFgQPN47RpcPCg3Swi+TVnDvz+O1SqBB062E7jcipwREQK6q67oEEDs6qxtm8QT5CVlTturG9fCAqyGqcoqMARESkoP7/cXpzx47V9g7i/jz6Cn34yyx08+qjtNEVCBY6IyKW47z6zfcPBgzBrlu00Ihf24ovmsUcPCA21m6WIqMAREbkUxYrlLpL20ktmXRERd/TNN2ZbhsDA3C1HfIAKHBGRS/XII1CuHOzYAR98YDuNyLll9948/LDXbstwLipwREQuValSuRsVjhkDTqfdPCJ/t2ULfPihGTeWvYaTj1CBIyJyOXr1guBgWLcOVq60nUYkr5deMo+tW0PNmnazFDEVOCIil6NCBejc2bSzbwWIuIPff4e33jLtQYPsZrFABY6IyOVKSDCrwn7yCWzcaDuNiPHaa3DqFNx+O9xyi+00RU4FjojI5apRA/77X9PWJpziDo4cgUmTTNsHe29ABY6ISOHI/hCZM0ebcIp9kyaZTTVvuAFatrSdxgoVOCIihaFRI/jXv8x6OBqLIzadOGFuT4GZOeXnZzePJSpwREQKy1NPmccZM2DfPrtZxHfNmgUpKXD11fDgg7bTWKMCR0SksPzjH9CkCZw8CS+/bDuN+KJTp2D0aNMeOBCKF7ebxyIVOCIihcXPL7cXZ9Iks0+VSFGaMwd27YKKFaFrV9tprFKBIyJSmJo3h5tuguPHc8dBiBSFzEwYOdK0n3gCSpSwm8cyFTgiIoXJzw+efNK0x4+HtDS7ecR3vP8+/Pyz2R+tRw/baaxTgSMiUtj+8x+oXdsUN2+8YTuN+IKsLHjuOdPu2xdKl7Yaxx2owBERKWz+/pCYaNqvvmpuV4m40uLFsGkThIRA796207gFFTgiIq7w4INQrRr88QdMnWo7jXgzpzO396ZXLyhTxmocd+HSAufQoUO0b9+ekJAQypQpQ5cuXTh27NgFX3PnnXfi5+eX5+jxt3uJu3fvplWrVpQsWZKKFSsyYMAATp8+7cq3IiJSMMWK5a5uPGaMmTou4gqffQbffQclS5rbUwK4uMBp3749mzdvZtmyZSxZsoRVq1bRvXv3i76uW7du7N+/P+d48YxVQTMzM2nVqhUnT57km2++Yfbs2cyaNYthw4a58q2IiBRcp04QEWF2dX7zTdtpxBs5nTBihGk/+qjZ3V4A8HM6nU5XXHjLli3UqVOHdevW0ahRIwCWLl1Ky5Yt2bt3LxEREed83Z133kn9+vUZO3bsOb//ySef8O9//5t9+/YRFhYGwKRJkxg0aBB//PEHgYGBF83mcDgIDQ0lLS2NkJCQS3uDIiL58eqrZrfxa66BrVtNz45IYVm5Eu68EwIDzR5o5/ls9RYF+fx2WQ/O6tWrKVOmTE5xAxATE4O/vz9r1qy54Gvfeecdypcvzw033EBiYiLHzxigt3r1aurWrZtT3ADExsbicDjYvHnzOa+XkZGBw+HIc4iIFInu3aF8efj1V5g/33Ya8TbZY2+6dPH64qagXFbgpKSkULFixTzPFStWjHLlypGSknLe1z300EO8/fbbLF++nMTERN566y06dOiQ57pnFjdAztfnu+6oUaMIDQ3NOSIjIy/1bYmIFEypUtCvn2k/95xZjE2kMHz7LXz+uekVHDjQdhq3U+ACZ/DgwWcNAv77sXXr1ksO1L17d2JjY6lbty7t27fnzTffZMGCBfz666+XfM3ExETS0tJyjj179lzytURECqxXL7P42tat6sWRwvP88+bx4YehalWrUdxRgW8G9+/fn06dOl3wnOrVqxMeHs6BAwfyPH/69GkOHTpEeHh4vn9eVFQUANu3b+eaa64hPDyctWvX5jknNTUV4LzXDQoKIigoKN8/U0SkUIWEQP/+Zp+qZ5+Ftm0hIMB2KvFk69fDkiVmzaXBg22ncUsFLnAqVKhAhXyM0o6OjubIkSOsX7+ehg0bAvDFF1+QlZWVU7TkR3JyMgCVKlXKue7zzz/PgQMHcm6BLVu2jJCQEOrUqVPAdyMiUkR69zY7jG/bBvPmQfv2thOJJxs+3Dy2bw/XXWc3i5ty2Ric2rVr07x5c7p168batWv5+uuv6dWrF+3atcuZQfX7779Tq1atnB6ZX3/9lREjRrB+/Xp+++03Fi1aRFxcHP/4xz+48cYbAWjWrBl16tTh4Ycf5ocffuDTTz9lyJAhxMfHq5dGRNxX6dJmA0QwvTgaiyOXas0a+Ogj0ws4dKjtNG7LpevgvPPOO9SqVYumTZvSsmVLbrvtNqZMmZLz/VOnTrFt27acWVKBgYF8/vnnNGvWjFq1atG/f3/uvfdeFi9enPOagIAAlixZQkBAANHR0XTo0IG4uDieffZZV74VEZHL16sXXHml2RBx7lzbacRTZffePPwwXHut3SxuzGXr4LgzrYMjItaMHm32qbruOti8WeviSMF88w00aWJ6b37+GapXt52oSLnFOjgiInIO8fHqxZFLl91707mzzxU3BaUCR0SkKJUuDQMGmPaIEaB99CS/Vq3KXffmqadsp3F7KnBERIpafLxZ3fiXX7RHleRfdu9Nly5a9yYfVOCIiBS1K66AJ5807aefhowMq3HEAyxfDitWmD2nsv/syAWpwBERsaFnT7j6atizByZPtp1G3JnTmXtLqmtXqFzZbh4PoQJHRMSG4GAYNsy0n38ejh2zm0fc1+LFsHo1lCgBQ4bYTuMxVOCIiNjSqRPUqAEHDsC4cbbTiDvKzMztvXn8cfjfqv5ycSpwRERsKV7crGoM8OKLcPiw3TzifubOhU2boEwZ7RheQCpwRERsatsW6taFtDQYM8Z2GnEnJ0/m3sYcNAjKlrWbx8OowBERscnfH557zrRfew1SUuzmEfcxdSrs3GluS/XpYzuNx1GBIyJi2913Q1QUHD9uFv8TSU/P/bMwdCiULGk3jwdSgSMiYpufn9mjCmDKFLONg/i2116D1FS45hozNVwKTAWOiIg7uPNOaNXKbN2QmGg7jdj0559m0DmYQejFi9vN46FU4IiIuIsXXjBjcj74AL7+2nYaseXZZ82g83r1oF0722k8lgocERF3cf318Mgjpj1ggFnBVnzLL7/AG2+Y9ssvm4JXLol+cyIi7uSZZ8yA0tWrTU+O+JZBg8xtypYtoWlT22k8mgocERF3EhEB/fub9uDBcOqU3TxSdL78EhYsML02WhPpsqnAERFxNwMGQMWKsH27NuL0FVlZuYVtt25Qp47dPF5ABY6IiLspXRqeftq0n3nGDDgV7zZ/PqxbB1dcYf6by2VTgSMi4o66doVateDgQS3+5+1OnMhdGmDwYAgLs5vHS6jAERFxR8WLw6uvmvZrr8G2bXbziOu89hrs2gVXXQX9+tlO4zVU4IiIuKvmzXMX/0tIsJ1GXGHfvty9yEaO1JYMhUgFjoiIO3vlFdOb8/HH5hDvMmgQHDsGt9wCHTrYTuNVVOCIiLiz666Dxx837X794ORJu3mk8Hz9Nbz9ttmLbNw4LepXyPTbFBFxd0OHmmnjP/8Mr79uO40UhsxM6N3btB95BG6+2W4eL6QCR0TE3YWEwKhRpv3MM3DggN08cvmmT4fvv4fQUDP2RgqdChwREU/QqRM0bAgOh3Yb93SHD8OTT5r2M8+Y3jkpdCpwREQ8gb8/jB9v2jNmwFdf2c0jl27YMPjzT7O56mOP2U7jtVTgiIh4iuhos4w/QI8e2qfKEyUn5+4WPm6cmSEnLqECR0TEk4weDeXLw+bNuQsBimfIzDQFalYWPPAA3HWX7UReTQWOiIgnKVcOXnrJtJ95xqyAK57hjTfgu+/MwOKxY22n8XouLXAOHTpE+/btCQkJoUyZMnTp0oVjx46d9/zffvsNPz+/cx7vvfdeznnn+v68efNc+VZERNxHXBzccQccPw59+thOI/mxd2/uwOLRo6FSJbt5fICf0+l0uuriLVq0YP/+/UyePJlTp07RuXNnbr75ZubMmXPO8zMzM/njjz/yPDdlyhTGjBnD/v37ueKKK0xoPz9mzpxJ8+bNc84rU6YMwcHB+crlcDgIDQ0lLS2NkJCQS3x3IiIWbdkC9eqZcTgLF0Lr1rYTyYX897+wYIEZR/XVV1rU7xIV5PPbZQXOli1bqFOnDuvWraNRo0YALF26lJYtW7J3714iIiLydZ0GDRpw0003MX369NzQfn4sWLCANm3aXFI2FTgi4hWefNKsjxMZCT/9BP/7R6C4mQ8/hDZtoFgxs/bNDTfYTuSxCvL57bIScvXq1ZQpUyanuAGIiYnB39+fNWvW5Osa69evJzk5mS5dupz1vfj4eMqXL0/jxo2ZMWMGF6rTMjIycDgceQ4REY83ZAhUqwZ79sDgwbbTyLkcPQq9epn2gAEqboqQywqclJQUKv5t8aJixYpRrlw5UlJS8nWN6dOnU7t2bW699dY8zz/77LO8++67LFu2jHvvvZfHHnuM8dnrQ5zDqFGjCA0NzTkiIyML/oZERNxNyZIwdappT5gAK1ZYjSPn8NRTZvxN9epmyw0pMgUucAYPHnzegcDZx9atWy872F9//cWcOXPO2XszdOhQmjRpQoMGDRg0aBADBw5kzJgx571WYmIiaWlpOceePXsuO5+IiFto2hS6dzftLl0gPd1uHsm1YkXu4oyTJkGJElbj+JpiBX1B//796dSp0wXPqV69OuHh4Rz4234pp0+f5tChQ4SHh1/057z//vscP36cuLi4i54bFRXFiBEjyMjIICgo6KzvBwUFnfN5ERGvMGYMfPIJ7Nhhegw0Bdm+Y8egc2fT7t4d/vUvu3l8UIELnAoVKlChQoWLnhcdHc2RI0dYv349DRs2BOCLL74gKyuLqKioi75++vTp3HPPPfn6WcnJyZQtW1ZFjIj4ppAQc6uqeXOzOu5998Ftt9lO5dsGDIDffoMqVXLXLZIi5bIxOLVr16Z58+Z069aNtWvX8vXXX9OrVy/atWuXM4Pq999/p1atWqxduzbPa7dv386qVavo2rXrWdddvHgx06ZNY9OmTWzfvp2JEycycuRIemdvOy8i4otiY+GRR8DpNI/Hj9tO5LuWLTO3pMDsG1a6tN08PsqlE/HfeecdatWqRdOmTWnZsiW33XYbU6ZMyfn+qVOn2LZtG8f/9hdxxowZXH311TRr1uysaxYvXpwJEyYQHR1N/fr1mTx5Mq+88grDhw935VsREXF/L78MERHwyy9mhpUUvbQ0MxYKID5e2zFY5NKF/tyV1sEREa/18cfQqpVpf/aZxn4UtS5dTK9N9erw449QqpTtRF7FLdbBERERC1q2hMceM+24OPjb6vDiQh9+aIobPz+YNUvFjWUqcEREvM1LL0GdOpCSYnoUfK+jvujt2ZM7ayohAW6/3W4eUYEjIuJ1SpSAuXMhMBAWL4aJE20n8m6nT8NDD8Hhw9CoEYwcaTuRoAJHRMQ73XgjvPCCaffvD5s3283jzUaMMBtoli4N8+aZwlKsU4EjIuKt+vQxa+OcOGF6GE6csJ3I+6xcCc89Z9qTJsE119jNIzlU4IiIeCt/fzPYtUIFM6MnPl7jcQrTn39C+/aQlQWdOpkiUtyGChwREW8WFgZz5phiZ8YMmDbNdiLvkJlpZqn9/jvUrJm755S4DRU4IiLeLiYm9zZKr17wt9Xj5RIMH27WHAoONuNurrjCdiL5GxU4IiK+YPBgaNMGTp40e1VpfZxL9/778Pzzpj1tGtSvbzWOnJsKHBERX5C9+Nx115k1W9q1M9ObpWA2bjTjbcCsd9O+vdU4cn4qcEREfEVoKHzwgVlh94svTK+O5N+hQ6YXLD0dmjbNnYYvbkkFjoiIL7n+ejPYGMzmnJMn283jKU6fhgcfhB07oGpVmD8fihWznUouQAWOiIiveeABePpp037sMTNYVs7P6TRT7D/7DEqWhIUL4corbaeSi1CBIyLii4YNM2NJsrJMwbNhg+1E7mvECJgyxYxjevttqFfPdiLJBxU4IiK+yM/P3J5q2tSMKWnVCnbvtp3K/UybZqaEA0yYAP/5j908km8qcEREfFVgIPzf/8ENN5idx1u2NBtGirF4MTz6qGk/9RT07Gk3jxSIChwREV8WGgoffQSVKpkNOWNjIS3Ndir7Vq+Gtm3NLbzOnc1tKvEoKnBERHxd5crw6adm4Oy6dWaDTofDdip71qyBFi3gr79Mr9bkyeaWnngUFTgiIgJ168Lnn0PZsvDtt+aD/dgx26mK3jffwL/+ZXqxbr8d3n0Xihe3nUougQocEREx6tc3RU6ZMvD112bgcXq67VRF56uvzC26o0fhzjvhk0/MoojikVTgiIhIrptuMuu9hITAqlWmJ8cXxuSsXGluzR07ZmaWffSRihsPpwJHRETyuvlmMyYnu8i5805ITbWdynU+/tgUcunp5vbU4sVmQT/xaCpwRETkbLfcAitWQMWKkJwMTZrAtm22UxW+adPgnnvg+HHTg/Phh1CihO1UUghU4IiIyLk1aGDG4lSrBr/+CtHRsHy57VSFIzMTEhOhWzfTjotTceNlVOCIiMj51ahhZlXdcotZBLBZM7Oir9NpO9mlS0uD1q1h9Gjz9VNPwaxZZuFD8RoqcERE5MIqVoQvvoB27cyu2r16mR4PT5xhlZwMjRubQcTBwWZvqeee0zo3XkgFjoiIXFyJEjBnDrz8MgQEmMKgUSPP2aTT6YQ33jA9UT//DFdfDV9+Ce3b204mLqICR0RE8sfPDxISICnJbO2wdaspGEaNglOnbKc7v717zcrE8fGQkQH//rfpyWnUyHYycSEVOCIiUjB33AEbN5qdtU+dgiefNFPLv/vOdrK8MjNNr80NN5hp70FB8MorsGiR2ZZCvJoKHBERKbgrrzQ7kc+aZbZ3+OEHM7ala1ezM7ltX35p8sTHm0HFjRubXpt+/TTexkeowBERkUvj5wcdO5pbVQ89ZMa5TJ8O115rZib9+WfRZ/r+e7PFxD/+YcYHhYbC66+bPaZq1Sr6PGKNywqc559/nltvvZWSJUtSpkyZfL3G6XQybNgwKlWqRIkSJYiJieGXX37Jc86hQ4do3749ISEhlClThi5dunDMFzeEExFxFxUrwjvvmDVzGjc22x2MHAlVq5oek7/9f7zQZWWZ7SWaNTNbTXz8sRkI3b27WZwwPt58LT7FZQXOyZMnuf/+++nZs2e+X/Piiy8ybtw4Jk2axJo1ayhVqhSxsbGcOHEi55z27duzefNmli1bxpIlS1i1ahXdu3d3xVsQEZGCuPVWWL0aFiwwiwQeOwZjx8J115ktEGbOLNx9rbZuhWefhWuuMZtkLlsG/v7w4IPw008weTKEhRXezxOP4ud0una1plmzZtG3b1+OHDlywfOcTicRERH079+fJ554AoC0tDTCwsKYNWsW7dq1Y8uWLdSpU4d169bR6H+j35cuXUrLli3Zu3cvERER+crkcDgIDQ0lLS2NkJCQy3p/IiJyDk6nGdg7frzZlTv7o6Z4cVMINWtmVka+6SZzGyk/19uzB9asMeNrPvss79YRISHmdlm/fmblZfFKBfn8LlZEmS5q586dpKSkEBMTk/NcaGgoUVFRrF69mnbt2rF69WrKlCmTU9wAxMTE4O/vz5o1a/jPf/5zzmtnZGSQkZGR87XD4XDdGxERETM+p3lzc+zYAXPnmttYW7aYnbtXrsw9NyLCFCWVKplip0QJs6DgiRPwxx+wf79Zu+bvwxGKF4e77jJr2dx7rzbIlDzcpsBJ+d+o+7C/dSeGhYXlfC8lJYWKFSvm+X6xYsUoV65czjnnMmrUKJ555plCTiwiIvlSvboZdPzUU7B9u+l9Wb7cTCv/7TfYt88cF1OsGFx/Pdx+uxlEHBtrem5EzqFABc7gwYN54YUXLnjOli1bqOVmI9UTExNJSEjI+drhcBAZGWkxkYiIj6pRwxyPPWa+PnTIbOS5Y4fprXE44K+/TDETGAgVKphxNNdcY2ZnFS9uN794jAIVOP3796dTp04XPKd69eqXFCQ8PByA1NRUKlWqlPN8amoq9evXzznnwIEDeV53+vRpDh06lPP6cwkKCiIoKOiScomIiAuVK2eOm2+2nUS8TIEKnAoVKlChQgWXBKlWrRrh4eEkJSXlFDQOh4M1a9bkzMSKjo7myJEjrF+/noYNGwLwxRdfkJWVRVRUlEtyiYiIiOdx2TTx3bt3k5yczO7du8nMzCQ5OZnk5OQ8a9bUqlWLBQsWAODn50ffvn157rnnWLRoERs3biQuLo6IiAjatGkDQO3atWnevDndunVj7dq1fP311/Tq1Yt27drlewaViIiIeD+XDTIeNmwYs2fPzvm6QYMGACxfvpw777wTgG3btpF2xpoIAwcOJD09ne7du3PkyBFuu+02li5dSnBwcM4577zzDr169aJp06b4+/tz7733Mm7cOFe9DREREfFALl8Hxx1pHRwRERHPU5DPb+1FJSIiIl5HBY6IiIh4HRU4IiIi4nVU4IiIiIjXUYEjIiIiXkcFjoiIiHgdFTgiIiLidVTgiIiIiNdRgSMiIiJex2VbNbiz7MWbHQ6H5SQiIiKSX9mf2/nZhMEnC5yjR48CEBkZaTmJiIiIFNTRo0cJDQ294Dk+uRdVVlYW+/bto3Tp0vj5+RXqtR0OB5GRkezZs0f7XP2NfjcXpt/Phen3c2H6/ZyffjcX5km/H6fTydGjR4mIiMDf/8KjbHyyB8ff35+rr77apT8jJCTE7f+g2KLfzYXp93Nh+v1cmH4/56ffzYV5yu/nYj032TTIWERERLyOChwRERHxOipwCllQUBDDhw8nKCjIdhS3o9/Nhen3c2H6/VyYfj/np9/NhXnr78cnBxmLiIiId1MPjoiIiHgdFTgiIiLidVTgiIiIiNdRgSMiIiJeRwVOIZowYQJVq1YlODiYqKgo1q5dazuS21i1ahV33303ERER+Pn5sXDhQtuR3MaoUaO4+eabKV26NBUrVqRNmzZs27bNdiy3MXHiRG688cacRciio6P55JNPbMdyS6NHj8bPz4++ffvajuIWnn76afz8/PIctWrVsh3Lrfz+++906NCBK6+8khIlSlC3bl2+++4727EKhQqcQjJ//nwSEhIYPnw4GzZsoF69esTGxnLgwAHb0dxCeno69erVY8KECbajuJ2VK1cSHx/Pt99+y7Jlyzh16hTNmjUjPT3ddjS3cPXVVzN69GjWr1/Pd999x1133UXr1q3ZvHmz7WhuZd26dUyePJkbb7zRdhS3cv3117N///6c46uvvrIdyW0cPnyYJk2aULx4cT755BN++uknXn75ZcqWLWs7WuFwSqFo3LixMz4+PufrzMxMZ0REhHPUqFEWU7knwLlgwQLbMdzWgQMHnIBz5cqVtqO4rbJlyzqnTZtmO4bbOHr0qPPaa691Llu2zHnHHXc4H3/8cduR3MLw4cOd9erVsx3DbQ0aNMh522232Y7hMurBKQQnT55k/fr1xMTE5Dzn7+9PTEwMq1evtphMPFFaWhoA5cqVs5zE/WRmZjJv3jzS09OJjo62HcdtxMfH06pVqzz/DxLjl19+ISIigurVq9O+fXt2795tO5LbWLRoEY0aNeL++++nYsWKNGjQgKlTp9qOVWhU4BSCgwcPkpmZSVhYWJ7nw8LCSElJsZRKPFFWVhZ9+/alSZMm3HDDDbbjuI2NGzdyxRVXEBQURI8ePViwYAF16tSxHcstzJs3jw0bNjBq1CjbUdxOVFQUs2bNYunSpUycOJGdO3dy++23c/ToUdvR3MKOHTuYOHEi1157LZ9++ik9e/akT58+zJ4923a0QuGTu4mLuKv4+Hg2bdqkcQJ/U7NmTZKTk0lLS+P999+nY8eOrFy50ueLnD179vD444+zbNkygoODbcdxOy1atMhp33jjjURFRVGlShXeffddunTpYjGZe8jKyqJRo0aMHDkSgAYNGrBp0yYmTZpEx44dLae7fOrBKQTly5cnICCA1NTUPM+npqYSHh5uKZV4ml69erFkyRKWL1/O1VdfbTuOWwkMDKRGjRo0bNiQUaNGUa9ePV577TXbsaxbv349Bw4c4KabbqJYsWIUK1aMlStXMm7cOIoVK0ZmZqbtiG6lTJkyXHfddWzfvt12FLdQqVKls/6RULt2ba+5jacCpxAEBgbSsGFDkpKScp7LysoiKSlJ4wTkopxOJ7169WLBggV88cUXVKtWzXYkt5eVlUVGRobtGNY1bdqUjRs3kpycnHM0atSI9u3bk5ycTEBAgO2IbuXYsWP8+uuvVKpUyXYUt9CkSZOzlqT4+eefqVKliqVEhUu3qApJQkICHTt2pFGjRjRu3JixY8eSnp5O586dbUdzC8eOHcvzr6adO3eSnJxMuXLlqFy5ssVk9sXHxzNnzhw+/PBDSpcunTNuKzQ0lBIlSlhOZ19iYiItWrSgcuXKHD16lDlz5rBixQo+/fRT29GsK1269FljtUqVKsWVV16pMVzAE088wd13302VKlXYt28fw4cPJyAggAcffNB2NLfQr18/br31VkaOHMkDDzzA2rVrmTJlClOmTLEdrXDYnsblTcaPH++sXLmyMzAw0Nm4cWPnt99+azuS21i+fLkTOOvo2LGj7WjWnev3AjhnzpxpO5pbeOSRR5xVqlRxBgYGOitUqOBs2rSp87PPPrMdy21pmniutm3bOitVquQMDAx0XnXVVc62bds6t2/fbjuWW1m8eLHzhhtucAYFBTlr1arlnDJliu1IhcbP6XQ6LdVWIiIiIi6hMTgiIiLidVTgiIiIiNdRgSMiIiJeRwWOiIiIeB0VOCIiIuJ1VOCIiIiI11GBIyIiIl5HBY6IiIh4HRU4IiIi4nVU4IiIiIjXUYEjIiIiXkcFjoiIiHid/werX+Z7HypkCQAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"plt.plot(x, s, color='r') # Plot mit der Farbe Rot\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "e229b04c-8688-4457-982c-7a3f27c4254c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-6d559d4604922bd9",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Titel für den Plot setzen\n",
|
||
"\n",
|
||
"Um einem Plot einen Titel zu geben, wird die Funktion [plt.title](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.title.html) verwendet. \n",
|
||
"\n",
|
||
"Der Titel wird dabei als String übergeben, z. B. `plt.title(\"Mein Plot\")`. Dies hilft, die Darstellung zu beschreiben und Plots leichter interpretierbar zu machen."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 34,
|
||
"id": "ca46e07c-2f69-40cb-b58b-5278e13a048e",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-106786a4fca81b67",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGzCAYAAAAi6m1wAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAX9JJREFUeJzt3XlcVOXiBvDnzDAM+77LJqLiBigq4VKa5JppWWlXU8nlV7lU2sa9pbbczLZbmlez3CpTs5tlVrjgloqiKC6ICwqyySYyw77MnN8f4BS5gTKcWZ7v5zOfG8OZwzOj13l457zvK4iiKIKIiIjIhMikDkBERETU0lhwiIiIyOSw4BAREZHJYcEhIiIik8OCQ0RERCaHBYeIiIhMDgsOERERmRwWHCIiIjI5LDhERERkclhwiEivAgMDMXnyZKlj3JOMjAwIgoA1a9ZIHYWImogFh4juyqlTp/D4448jICAAVlZWaNOmDR566CEsWbJE6mhNtmfPHgiCoLspFAoEBQVh4sSJuHTpUov8jIMHD2LBggUoKSlpkfMRUdNYSB2AiIzPwYMHMXDgQPj7+2PatGnw8vJCVlYWDh06hM8++wyzZs3SHXvu3DnIZIb9u9Ts2bPRq1cv1NbW4tixY1ixYgV+/fVXnDp1Cj4+Pvd07oMHD+Ktt97C5MmT4eTk1DKBieiOWHCIqNn+/e9/w9HREUeOHLnhTbugoKDR10qlshWT3Z3+/fvj8ccfBwDExMSgQ4cOmD17NtauXYvY2FiJ0xHR3TDsX6uIyCBdvHgRXbp0uemIhIeHR6Ov/34Nzpo1ayAIAg4cOIA5c+bA3d0dtra2ePTRR1FYWNjosYIgYMGCBTf8jL+fs7a2Fm+99Rbat28PKysruLq6ol+/ftixY8ddPb8HH3wQAJCenn7b43bt2oX+/fvD1tYWTk5OGDVqFFJTU3XfX7BgAV555RUAQNu2bXUfhWVkZNxVLiJqOo7gEFGzBQQEICEhAadPn0bXrl3v6hyzZs2Cs7Mz5s+fj4yMDHz66aeYOXMmNm7c2OxzLViwAAsXLsTUqVPRu3dvqNVqHD16FMeOHcNDDz3U7PNdvHgRAODq6nrLY3bu3Ilhw4YhKCgICxYsQGVlJZYsWYK+ffvi2LFjCAwMxGOPPYbz589j/fr1+M9//gM3NzcAgLu7e7MzEVHzsOAQUbO9/PLLGDZsGMLDw9G7d2/0798fgwYNwsCBA6FQKJp0DldXV2zfvh2CIAAAtFotFi9eDJVKBUdHx2bl+fXXXzF8+HCsWLGi2c8FAEpLS1FUVITa2locP34cL7zwAgRBwJgxY275mFdeeQUuLi5ISEiAi4sLAGD06NHo3r075s+fj7Vr1yI0NBQ9evTA+vXrMXr0aAQGBt5VPiJqPn5ERUTN9tBDDyEhIQGPPPIITpw4gQ8++ABDhgxBmzZtsGXLliadY/r06bpyA9RfB6PRaHD58uVm53FyckJKSgouXLjQ7McCwDPPPAN3d3f4+PhgxIgRKC8vx9q1a9GzZ8+bHn/lyhUkJydj8uTJunIDAKGhoXjooYfw22+/3VUOImo5LDhEdFd69eqFH3/8EdeuXUNiYiJiY2NRWlqKxx9/HGfOnLnj4/39/Rt97ezsDAC4du1as7O8/fbbKCkpQYcOHdCtWze88sorOHnyZJMfP2/ePOzYsQO7du3CyZMnkZubi6effvqWx18vYR07drzhe506dUJRURHKy8ub/TyIqOWw4BDRPbG0tESvXr3w3nvvYdmyZaitrcWmTZvu+Di5XH7T+0VRvONjNRpNo6/vv/9+XLx4EatWrULXrl3x1VdfoUePHvjqq6+a9By6deuG6OhoDBw4EN26dYOFBT+9JzJ2LDhE1GKuf6Rz5cqVFjmfs7PzDQvk1dTU3PT8Li4uiImJwfr165GVlYXQ0NCbzsBqCQEBAQDq1/j5u7Nnz8LNzQ22trYA0OhjOCJqPSw4RNRsu3fvvulIy/VrT2720c3daNeuHfbt29fovhUrVtwwgnP16tVGX9vZ2SE4OBjV1dUtkuPvvL29ER4ejrVr1zYqYKdPn8b27dsxfPhw3X3Xiw5XMiZqXRyHJaJmmzVrFioqKvDoo48iJCQENTU1OHjwIDZu3IjAwEDExMS0yM+ZOnUqnn32WYwZMwYPPfQQTpw4gW3btummW1/XuXNnDBgwABEREXBxccHRo0fxww8/YObMmS2S42Y+/PBDDBs2DFFRUZgyZYpumrijo2OjkaOIiAgAwL/+9S+MGzcOCoUCI0eO1BUfItIPFhwiaraPPvoImzZtwm+//YYVK1agpqYG/v7+eP755/HGG2+02JYE06ZNQ3p6OlauXIm4uDj0798fO3bswKBBgxodN3v2bGzZsgXbt29HdXU1AgIC8O677+oW2dOH6OhoxMXFYf78+Zg3bx4UCgUeeOABLFq0CG3bttUd16tXL7zzzjtYvnw54uLioNVqkZ6ezoJDpGeC2JQr+oiIiIiMCK/BISIiIpPDgkNEREQmhwWHiIiITA4LDhEREZkcFhwiIiIyOSw4REREZHLMch0crVaL3Nxc2Nvbcxl1IiIiIyGKIkpLS+Hj4wOZ7PZjNGZZcHJzc+Hn5yd1DCIiIroLWVlZ8PX1ve0xZllw7O3tAdS/QA4ODhKnISIioqZQq9Xw8/PTvY/fjlkWnOsfSzk4OLDgEBERGZmmXF7Ci4yJiIjI5LDgEBERkclhwSEiIiKTw4JDREREJocFh4iIiEwOCw4RERGZHBYcIiIiMjksOERERGRyWHCIiIjI5LDgEBERkcnRa8HZt28fRo4cCR8fHwiCgJ9++umOj9mzZw969OgBpVKJ4OBgrFmz5oZjli5disDAQFhZWSEyMhKJiYktH56IiIiMll4LTnl5OcLCwrB06dImHZ+eno4RI0Zg4MCBSE5OxosvvoipU6di27ZtumM2btyIOXPmYP78+Th27BjCwsIwZMgQFBQU6OtpEBERkZERRFEUW+UHCQI2b96M0aNH3/KY1157Db/++itOnz6tu2/cuHEoKSlBXFwcACAyMhK9evXC559/DgDQarXw8/PDrFmz8Prrr9/0vNXV1aiurtZ9fX03UpVKxc02zVhVrQbpReVILypHYWk1rpZVo7pOi1qNCIWFAHulBZxsLOHrbA1/FxsEuNpCLrvzBm9ERKQfarUajo6OTXr/NqjdxBMSEhAdHd3oviFDhuDFF18EANTU1CApKQmxsbG678tkMkRHRyMhIeGW5124cCHeeustvWQm41FeXYd95wuRcOkqEtOLcT6/FNpm1HtbSzm6tHFE70AX3N/BHd39naCQ8zI2IiJDZFAFJy8vD56eno3u8/T0hFqtRmVlJa5duwaNRnPTY86ePXvL88bGxmLOnDm6r6+P4JDpq67TYMeZfGw+loM/0opQU6dt9H17KwsEe9jBy8EKbnZKWFvKIZcJqK3Toqy6DkVlNci+VoGMq+Uor9EgMb0YienF+Hx3GpxsFBjW1Rujw33Qu60LBIGjO0REhsKgCo6+KJVKKJVKqWNQKypQV2HVgQxsPJKJaxW1uvsDXW0woKMHegW6oEeAE7wcrJpUTDRaERcLy5CcWYL9aUXYn1aE4vIarE/MxPrETLT3sMPEqACMifCFjaVZ/N+KiMigGdS/xF5eXsjPz290X35+PhwcHGBtbQ25XA65XH7TY7y8vFozKhmoK6pKLI5Pw/+SslGjqR+t8XKwwpiINhgV3gbtPezuaqRFLhPQwdMeHTzt8WQvP2i0Ig5fuoqfk3Ox9WQuLhSU4c2fU/DpzguYfn8QJtwXAFulQf3fi4jIrBjUv8BRUVH47bffGt23Y8cOREVFAQAsLS0RERGB+Ph43cXKWq0W8fHxmDlzZmvHJQNSWlWLz3elYc3BDFQ3fAzVM8AZ0+4PQnQnzxa/OFguE9An2A19gt3wr4c74cekbKw8kI6s4kos/P0svtqfjleGdMTjPXwh44XJREStTq8Fp6ysDGlpabqv09PTkZycDBcXF/j7+yM2NhY5OTn4+uuvAQDPPvssPv/8c7z66qt45plnsGvXLnz//ff49ddfdeeYM2cOJk2ahJ49e6J379749NNPUV5ejpiYGH0+FTJQoihiy4lcvPtrKgpL62fK9Q50wctDOqJ3W5dWyeBgpcDkvm0x/r4A/HQ8B4t3XUBWcSVe/eEkvk7IwPuPhaJrG8dWyUJERPX0Ok18z549GDhw4A33T5o0CWvWrMHkyZORkZGBPXv2NHrMSy+9hDNnzsDX1xdvvvkmJk+e3Ojxn3/+OT788EPk5eUhPDwcixcvRmRkZJNzNWeaGRmuPFUVXv/xJPacKwRQf33NvJGdMbCjh6QX/FbXabD2YAaWxKehtLoOcpmAKf3aYs5DHWClkEuWi4jI2DXn/bvV1sExJCw4xu/n5By88dNplFbVwdJChlkDgzH9gSAoLQynQBSWVuOtX1Kw9eQVAEAHTzt8OrY7Ovvw7xwR0d1gwbkDFhzjVVmjwYItKdh4NAsAEObriI+eCEN7T3uJk93azjP5eP3HUygqq4alXIZ/jeiEiVEBnFZORNRMLDh3wIJjnDKvVmDa10dxLr8UggDMGhiM2YPaw8IIFtsrKqvG6/87iZ2p9VuKjA73wXuPdeOUciKiZmjO+7fhvzMQATiQVoRHlu7HufxSuNkpsW5KJOYM7mgU5QYA3OyU+HJiT7wxohPkMgE/Jefisf8eRE5JpdTRiIhMknG8O5BZ25CYiYmrElFSUYswPyf8Orsf+gS7SR2r2QRBwNT+QfhuaiTc7JQ4m1eK0UsP4ERWidTRiIhMDgsOGSxRFPHJjvN4/cdT0GhFPNa9DTZOvw+eDlZSR7snkUGu+GlGH4R42aOwtBpjVyRg19n8Oz+QiIiajAWHDJJGK+Kfm09hcfwFAMDsQe3x8ZNhJjPN2tfZBpuejcKAju6oqtVi2tdJ+PFYttSxiIhMBgsOGZxajRZzvk/G+sQsyARg4WPdMOehDiY368jeSoEvJ/bEo93bQKMVMef7E/j20GWpYxERmQRO4SCDUqvRYtZ3xxGXkgcLmYDPxnXHiFBvqWPpjUIuw8dPhMHJRoHVBzLwxk+nYSETMK63v9TRiIiMGgsOGQyNVsTLm04gLiUPlhYyLJ/QAw+GeEodS+9kMgHzHu4MAQJWHUhH7OZTkMsEPNHTT+poRERGix9RkUEQRRFv/HQKPyfnwkImYNl48yg31wmCgDcf7oRJUQEQReDV/53E5uO8JoeI6G6x4JDkRFHEu7+m6q65+c/YcAzqZD7l5jpBELDgkS4YH+kPUQTmfn8CW07kSh2LiMgoseCQ5P6z8wJW7k8HALw/JhQjw3wkTiQdQRDwzqiuGNfLD1oRmLMxGfsvFEkdi4jI6LDgkKS+ScjQTQVfMLIznuR1J5DJBLz3aDc8EuaDOq2I575Nwrm8UqljEREZFRYcksze84VY8MsZAMDchzpgct+2EicyHDKZgA+fCEXvQBeUVtchZnUi8tVVUsciIjIaLDgkifP5pZi57hg0WhFjevhi5oPBUkcyOEoLOVZMjECQuy1yVVV4Zs0RlFfXSR2LiMgosOBQqysqq8Yza46gtLoOvdu6YOFj3UxuEb+W4mRjiTWTe8PV1hIpuWrM/O4Y6jRaqWMRERk8FhxqVVW1Gkz/+iiyr1UiwNUGX0yIgKUF/xrejr+rDVZO7gUrhQy7zxXivd/OSh2JiMjg8Z2FWo0oioj98RSOZZbAwcoCqyb3grOtpdSxjEK4nxM+HRsOAFh1IJ3Tx4mI7oAFh1rNt4cuY/PxHMhlApZNiEA7dzupIxmVoV298fyAdgCA1344yZlVRES3wYJDrSI5qwRvb62fMRU7LAR9g90kTmSc5g7uiH7Bbqis1eDZb5OgrqqVOhIRkUFiwSG9u1ZegxnrjqFWI2JIF09M6cfp4HdLLhOw+KnuaONkjfSicsz9/gS0WlHqWEREBocFh/RKqxUx5/tk5JTUX1T84RNhnDF1j1xsLbFsQg9YWsiw40w+lu29KHUkIiKDw4JDerVs70XsPlcIpYUM/x3fAw5WCqkjmYRQXye8M6oLAODj7eeQmF4scSIiIsPCgkN6c+jSVXy8/RwA4J1RXdHFx1HiRKZlbC9/jOnhC60IvLQxGapKXo9DRHQdCw7phaqyFnM2JkMrAmN6+OLJXtxjSh/eGtUFAa42yCmpxL82n4Io8nocIiKABYf0ZN7Pp5GrqkKAqw3ebvgohVqendICn43rDguZgK0nr+B/x3KkjkREZBBYcKjF/Zycg5+TcyGXCfjP2HDYKi2kjmTSwv2c8NJDHQDUF8uMonKJExERSY8Fh1pUbkkl3vjpNABg5sBg9PB3ljiReXj2gXaIbOuCihoNXthwHLXcr4qIzBwLDrUYrVbE3O9PoLSqDuF+TtwhvBVdHy1zsLLAiWwVlsRfkDoSEZGkWHCoxazcn46ES1dhrZDjP2PDoZDzr1dr8nGyxnuPdQMALN1zEadzVBInIiKSDt+BqEWkFZThw4Yp4fNGdkZbN1uJE5mnh0N9MLybFzRaEa/8cBI1dfyoiojMU6sUnKVLlyIwMBBWVlaIjIxEYmLiLY8dMGAABEG44TZixAjdMZMnT77h+0OHDm2Np0I3odWKeP1/9W+mD3RwxzhOCZfU26O6wtlGgdQraizbw1WOicg86b3gbNy4EXPmzMH8+fNx7NgxhIWFYciQISgoKLjp8T/++COuXLmiu50+fRpyuRxPPPFEo+OGDh3a6Lj169fr+6nQLXxz6DKOXr4GW0s53nusG7dikJibnRILHqmfmr9k1wWkXlFLnIiIqPXpveB88sknmDZtGmJiYtC5c2csX74cNjY2WLVq1U2Pd3FxgZeXl+62Y8cO2NjY3FBwlEplo+OcnW89W6e6uhpqtbrRjVpG9rUKLIo7CwB4fVgI2jhZS5yIAOCRMB881NkTdVoRr/xwgrOqiMjs6LXg1NTUICkpCdHR0X/+QJkM0dHRSEhIaNI5Vq5ciXHjxsHWtvE1HXv27IGHhwc6duyI5557DlevXr3lORYuXAhHR0fdzc+PH6G0BFEU8c/Np1FRo0GvQGeMjwyQOhI1EAQB/x7dFY7WCpzOUWPFvktSRyIialV6LThFRUXQaDTw9PRsdL+npyfy8vLu+PjExEScPn0aU6dObXT/0KFD8fXXXyM+Ph6LFi3C3r17MWzYMGg0mpueJzY2FiqVSnfLysq6+ydFOv87loN95wthaSHD+2NCIZPxoylD4uFghfkjOwMAPtt5ARcLyyRORETUegx6idmVK1eiW7du6N27d6P7x40bp/vvbt26ITQ0FO3atcOePXswaNCgG86jVCqhVCr1ntecFJRW4Z2tZwAAL0a3Rzt3O4kT0c082r0NtpzIxZ5zhXjzp9NYNzWS10gRkVnQ6wiOm5sb5HI58vPzG92fn58PLy+v2z62vLwcGzZswJQpU+74c4KCguDm5oa0tLR7yktN9+7WVKgqa9HFxwHT+gdJHYduQRAEvP1IVygtZDh48Sp+Ts6VOhIRUavQa8GxtLREREQE4uPjdfdptVrEx8cjKirqto/dtGkTqqurMWHChDv+nOzsbFy9ehXe3t73nJnu7GBaEbacyIUgAO8/FsoF/Qycv6sNZg9qDwB499czUFXUSpyIiEj/9P7ONGfOHHz55ZdYu3YtUlNT8dxzz6G8vBwxMTEAgIkTJyI2NvaGx61cuRKjR4+Gq6tro/vLysrwyiuv4NChQ8jIyEB8fDxGjRqF4OBgDBkyRN9Px+zV1Gnx5s/1e01NiAxAN19HiRNRU0zrH4RgDzsUldXgg21npY5DRKR3er8GZ+zYsSgsLMS8efOQl5eH8PBwxMXF6S48zszMhEzWuGedO3cO+/fvx/bt2284n1wux8mTJ7F27VqUlJTAx8cHgwcPxjvvvMPrbFrByv3puFhYDldbS7w8uKPUcaiJLC1keHd0V4xbcQjfJWZiTIQvN0IlIpMmiKIoSh2itanVajg6OkKlUsHBwUHqOEYjp6QS0R/vRWWtBh8/EYYxEb5SR6JmmvN9Mn48loNO3g74ZWZfWPDjRSIyIs15/+a/btRkb/+SgspaDXoHuuCxHm2kjkN34Z/DO8HRun4bh7UJl6WOQ0SkNyw41CS7zxVgW0o+5DIBb4/uwqnGRsrNTonXhoYAAD7deR5FZdUSJyIi0g8WHLqj6joNFmxJAQDE9AlEiBc/1jNmY3v5oWsbB5RW1eHjhh3giYhMDQsO3dHqAxm4fLUCHvZKvPhQB6nj0D2SywTMH1m/GeeGI1k4naOSOBERUctjwaHbKiytxue76hdQfHVoCOyUBr34NTVRr0AXjAzzgSgCb/2SAjOca0BEJo4Fh27r4+3nUFZdh1BfRzzWnRcWm5LYYSGwUshwJOMatp68InUcIqIWxYJDt5SSq8LGo/Ubk857uDM30zQxPk7WeO6BYADAwt9SUVlz881qiYiMEQsO3ZQoinj7lzMQReDhUG/0DHSROhLpwf89EIQ2TtbIVVVh+d6LUschImoxLDh0U9tS8nE4vRhKCxleHxYidRzSEyuFHP8c3gkAsHzvReSWVEqciIioZbDg0A2q6zR477dUAMD0+4Pg62wjcSLSp+HdvNA70AXVdVp8vP281HGIiFoECw7dYM2BDGQW108Lf/aBdlLHIT0TBAH/HFE/ivPj8WycyVVLnIiI6N6x4FAjJRU1WLq7flr4K0M6wpbTws1CuJ8THg71higCC39PlToOEdE9Y8GhRv675yLUVXUI8bLHYz24maY5eXVICBRyAX9cKMK+84VSxyEiuicsOKSTU1KJNQczAACvDQ2BnNPCzYq/qw2evi8QALDw97PQaLn4HxEZLxYc0vl4+znU1GlxX5ALBnR0lzoOSWDWg8Gwt7JA6hU1Nh/PkToOEdFdY8EhAMCZ3D/f0GKHdeJu4WbK2dYSMwbWL/738fZzqKrl4n9EZJxYcAgA8MG2sxBFYESoN8L8nKSOQxKa3CcQbZyscUVVhVUH0qWOQ0R0V1hwCAcvFmHPuUJYyAS8Mrij1HFIYlYKOeYOrt81fvmei1BV1EqciIio+VhwzJwoinj/97MAgPGR/gh0s5U4ERmCUeFt0NHTHuqqOqz4g1s4EJHxYcExc9tS8nAyWwVbSzlmDWovdRwyEHKZoBvFWbU/A4Wl1RInIiJqHhYcM6bRirql+af0aws3O6XEiciQPNTZE2F+Tqis1egWfyQiMhYsOGbslxO5uFBQBgcrC0zpHyR1HDIwgvDnNVnfHc5EDjfiJCIjwoJjpmo1WvxnZ/3ozf890A6O1gqJE5Eh6hvsiqggV9RotFi884LUcYiImowFx0z9Lykbl69WwM3OEjF9A6WOQwZKEAS8PKR+FOeHY9m4WFgmcSIioqZhwTFD1XUaLI6v/238uQHBsLHkhpp0axEBzoju5AGNVsR/dpyXOg4RUZOw4Jih9YczkauqgpeDFcZH+ksdh4zA3IZrcbaevIIzuWqJ0xAR3RkLjpmprNHg893165rMGhQMK4Vc4kRkDDp5O+DhUG8AwGfxHMUhIsPHgmNmvk7IQFFZNfxdbPBkTz+p45AReWFQewgCsC0lHym5KqnjEBHdFguOGSmvrsMX+y4BAGYPag+FnH/81HTtPe3xcKgPAOAzzqgiIgPHdzgz8u2hyygur0Ggqw1Gh/tIHYeM0AuDgiEIwPYz+Tidw1EcIjJcLDhmoqKmDisaRm9mPtgeFhy9obsQ7GGPkddHceI5ikNEhqtV3uWWLl2KwMBAWFlZITIyEomJibc8ds2aNRAEodHNysqq0TGiKGLevHnw9vaGtbU1oqOjceEC/7G9nXWHMnG1vAYBHL2hezS74VqcHRzFISIDpveCs3HjRsyZMwfz58/HsWPHEBYWhiFDhqCgoOCWj3FwcMCVK1d0t8uXLzf6/gcffIDFixdj+fLlOHz4MGxtbTFkyBBUVVXp++kYpcoaDb7YVz9zasbAYI7e0D0J9rDDI2H1JflTXotDRAZK7+90n3zyCaZNm4aYmBh07twZy5cvh42NDVatWnXLxwiCAC8vL93N09NT9z1RFPHpp5/ijTfewKhRoxAaGoqvv/4aubm5+Omnn256vurqaqjV6kY3c7Lu8GUUldXAz8Uaj3ZvI3UcMgGzHmwPmQDsTOUoDhEZJr0WnJqaGiQlJSE6OvrPHyiTITo6GgkJCbd8XFlZGQICAuDn54dRo0YhJSVF97309HTk5eU1OqejoyMiIyNvec6FCxfC0dFRd/PzM5/p0ZU1GizfW3/tzayBnDlFLYOjOERk6PT6bldUVASNRtNoBAYAPD09kZeXd9PHdOzYEatWrcLPP/+Mb7/9FlqtFn369EF2djYA6B7XnHPGxsZCpVLpbllZWff61IzGd4mZKCqrrh+96cHRG2o5sxquxdmZmo+zeeY1KkpEhs/gfp2PiorCxIkTER4ejgceeAA//vgj3N3d8cUXX9z1OZVKJRwcHBrdzEFVrQbL9zZcezMgmKM31KLaudtheLf61Y2XNqyOTURkKPT6jufm5ga5XI78/PxG9+fn58PLy6tJ51AoFOjevTvS0tIAQPe4ezmnudh0NAuFpdVo42SNx3r4Sh2HTNCMAcEAgF9P5iK9qFziNEREf9JrwbG0tERERATi4+N192m1WsTHxyMqKqpJ59BoNDh16hS8vet/U2zbti28vLwanVOtVuPw4cNNPqc5qNVoddfePPtAECwtOHpDLa+zjwMGhXhAKwLL9qRJHYeISEfv73pz5szBl19+ibVr1yI1NRXPPfccysvLERMTAwCYOHEiYmNjdce//fbb2L59Oy5duoRjx45hwoQJuHz5MqZOnQqgfobViy++iHfffRdbtmzBqVOnMHHiRPj4+GD06NH6fjpGY0tyLnJKKuFmp8QT3HOK9GjGg/WjOD8ey0FOSaXEaYiI6lno+weMHTsWhYWFmDdvHvLy8hAeHo64uDjdRcKZmZmQyf7sWdeuXcO0adOQl5cHZ2dnRERE4ODBg+jcubPumFdffRXl5eWYPn06SkpK0K9fP8TFxd2wIKC50mpF/Lfht+mp/dtyx3DSqx7+zogKckXCpatYsfci3hrVVepIREQQRFEUpQ7R2tRqNRwdHaFSqUzyguO401fw7LfH4GBlgQOvPwh7K4XUkcjEHUgrwvivDkNpIcP+1x6Eu71S6khEZIKa8/7NCzNMjCiKuhktk/sEstxQq+jTzhXhfk6ortPiq/2XpI5DRMSCY2r+uFCEUzkqWCvkmNy3rdRxyEwIgoCZA+uvxfk24TJKKmokTkRE5o4Fx8Qs3V1/7c0/Iv3hYmspcRoyJ4M6eSDEyx7lNRqsOZghdRwiMnMsOCbkaEYxDqcXQyEXMK1/kNRxyMwIgoAZDaM4qw9koKy6TuJERGTOWHBMyH/31F9783iEL7wcOaOMWt/wbt4IcrOFqrIW3x2+LHUcIjJjLDgmIiVXhV1nCyATgP+7v53UcchMyWUCnh1Q//fvyz/SUVWrkTgREZkrFhwTsaxh9GZEqA8C3WwlTkPm7NHubdDGyRqFpdXYdNR8NrYlIsPCgmMCLhWW4ddTVwAAzw/g6A1JSyGX4f8eqL8G7Ms/0lGn0UqciIjMEQuOCfhi7yWIIjAoxAOdvE1v4UIyPk9E+MHZRoHM4grEpeRJHYeIzBALjpHLU1Xhx+PZAIDnB3L0hgyDtaUck/oEArhewM1uwXQikhgLjpFbfTAdtRoRvQNdEBHgInUcIp2JUYGwUshwKkeFhEtXpY5DRGaGBceIlVbV4rtDmQCA6fdz3RsyLC62lniyYSf7L/Zy+wYial0sOEZsQ2IWSqvr0M7dFg+GeEgdh+gGU/sFQSYAe88XIvWKWuo4RGRGWHCMVK1Gi1UH0gHUj97IZILEiYhu5O9qg+HdvAEAK/ZxFIeIWg8LjpH65UQurqiq4G6vxOjubaSOQ3RL1xee/OVELnJKKiVOQ0TmggXHCImiqPtteHKfQCgt5BInIrq1br6O6NPOFXVaEav2p0sdh4jMBAuOEdp3oQhn80phYynHhMgAqeMQ3dH/PVA/irM+MROqilqJ0xCROWDBMUIr9tVvyzCulz8cbRQSpyG6s/vbuyHEyx4VNRp8y004iagVsOAYmdM5KhxIuwq5TMAz/QKljkPUJIIg6LZvWH0gg5twEpHeseAYmevX3jwc6g1fZxuJ0xA13cOhPvBxtEJRWTU2H8+ROg4RmTgWHCOSfa1Ct6kmF/YjY6OQyzClf8MmnPsuQaPl9g1EpD8sOEZk5f50aLQi+gW7oYuPo9RxiJptXC8/OFhZ4FJROXacyZc6DhGZMBYcI6GqqMXGI1kAOHpDxstWaYEJ99XP/OOUcSLSJxYcI/Ht4cuoqNGgk7cD+rd3kzoO0V2b1CcQCrmAxIxinMgqkToOEZkoFhwjUF2nwZqDGQCA6fe3hSBwWwYyXp4OVhgZ6gOg/mNXIiJ9YMExAltPXEFhaTW8HKzwcMMbA5Exe6ZfWwDAr6euIJfbNxCRHrDgGDhRFHW/5U7sEwCFnH9kZPy6tnFEVJArNFoRaxtGJ4mIWhLfLQ3coUvFOHNFDSuFDP/o7S91HKIWM7V//SjOd4mZKKuukzgNEZkaFhwDd330ZkwPXzjZWEqchqjlDOzogSA3W5RW1WHT0Syp4xCRiWHBMWAZReWIP1u/Vsj1axaITIVMJuj+Xq86kM6F/4ioRbHgGLDVB9IhisDAju5o524ndRyiFlc/MqlAVnEldpzJkzoOEZmQVik4S5cuRWBgIKysrBAZGYnExMRbHvvll1+if//+cHZ2hrOzM6Kjo284fvLkyRAEodFt6NCh+n4arUpVWYtNSdkAgCn9uLAfmSZrSzkmRNYv/PfVH5wyTkQtR+8FZ+PGjZgzZw7mz5+PY8eOISwsDEOGDEFBQcFNj9+zZw+eeuop7N69GwkJCfDz88PgwYORk9N4c76hQ4fiypUrutv69ev1/VRa1YbETFTUaBDiZY++wa5SxyHSm4lRAVDIBRy9fA3HM69JHYeITITeC84nn3yCadOmISYmBp07d8by5cthY2ODVatW3fT4devW4fnnn0d4eDhCQkLw1VdfQavVIj4+vtFxSqUSXl5eupuzs/MtM1RXV0OtVje6GbI6jVY3dfaZvlzYj0ybh4MVRoZx4T8iall6LTg1NTVISkpCdHT0nz9QJkN0dDQSEhKadI6KigrU1tbCxcWl0f179uyBh4cHOnbsiOeeew5Xr1695TkWLlwIR0dH3c3Pz+/unlAr+f10HnJVVXCzs8Qj4VzYj0zflIaLjX8/nYfsaxUSpyEiU6DXglNUVASNRgNPT89G93t6eiIvr2kXFL722mvw8fFpVJKGDh2Kr7/+GvHx8Vi0aBH27t2LYcOGQaPR3PQcsbGxUKlUultWlmFPSb3+W+z4yABYKeQSpyHSvy4+jujTjgv/EVHLsZA6wO28//772LBhA/bs2QMrKyvd/ePGjdP9d7du3RAaGop27dphz549GDRo0A3nUSqVUCqVrZL5XiVdvobkrBJYymW6XZeJzMHU/m1x8OJVbEjMwuxB7WFvpZA6EhEZMb2O4Li5uUEulyM/P7/R/fn5+fDy8rrtYz/66CO8//772L59O0JDQ297bFBQENzc3JCWlnbPmaW2qmH0ZlS4D9ztjaOUEbWEAR08EORui9LqOvzQMIOQiOhu6bXgWFpaIiIiotEFwtcvGI6Kirrl4z744AO88847iIuLQ8+ePe/4c7Kzs3H16lV4e3u3SG6pZF+rwO+nrwAApvTnwn5kXmQyATF9AgEAaw9mQMuF/4joHuh9FtWcOXPw5ZdfYu3atUhNTcVzzz2H8vJyxMTEAAAmTpyI2NhY3fGLFi3Cm2++iVWrViEwMBB5eXnIy8tDWVkZAKCsrAyvvPIKDh06hIyMDMTHx2PUqFEIDg7GkCFD9P109GrtwQxoRaBvsCtCvBykjkPU6h7r4Qt7KwtkXK3A7nM3X0qCiKgp9F5wxo4di48++gjz5s1DeHg4kpOTERcXp7vwODMzE1euXNEdv2zZMtTU1ODxxx+Ht7e37vbRRx8BAORyOU6ePIlHHnkEHTp0wJQpUxAREYE//vjDaK6zuZmy6jpsSKy/+HkKt2UgM2WrtMC4XvWzHFcfyJA2DBEZNUEURbMbB1ar1XB0dIRKpYKDg2GMlKw+kI63fjmDIHdb7HzpAchkXPuGzFNWcQUe+HA3tCKw/aX70cHTXupIRGQgmvP+zb2oDIBGK+p+W43p25blhsyan4sNHupcP8LLURwiulssOAZgZ2o+Mosr4GitwJgebaSOQyS5mL71H9NuPp6NkooaidMQkTFiwTEA1xf2+0ekP2wsDXppIqJWEdnWBZ29HVBVq8X6RMNemJOIDBMLjsRSclVITC+GXCZgYhQX9iMCAEEQENM3EADwTUIG6jRaaQMRkdFhwZHY9WXph3X1grejtbRhiAzIyDAfuNpaIldVhW0p+Xd+ABHRX7DgSKi4vAY/JecCgO63VSKqZ6WQY3ykPwBg1QHuMk5EzcOCI6H1iZmoqdOiWxtH9PB3ljoOkcGZcF8AFHIBSZev4WR2idRxiMiIsOBIpFajxbeHLgMAJvcJhCBwajjR33k4WGFEt/otWDhlnIiagwVHIttT8nFFVQU3O0s8HGbce2gR6dP1KeNbT+aiQF0lcRoiMhYsOBJZc7Bhanhvfygt5BKnITJcYX5O6OHvhFqNiG8PZ0odh4iMBAuOBE7nqHAk4xosZALG38ep4UR38kzD/mzfHb6M6jqNxGmIyBiw4EhgTcPU8OHdvOHpYCVtGCIjMKSLF7wdrVBUVoNfTly58wOIyOyx4LSyorJqbGmYGj6ZU8OJmkQhl+HphoUwVx9IhxnuEUxEzcSC08o2JGaiRqNFmK8juvs5SR2HyGg81csfVgoZUnLVOJJxTeo4RGTgWHBaUa1Gi2+uTw3vy6nhRM3hbGuJR7vXb0a7mgv/EdEdsOC0orjTechXV8PNTonh3Tg1nKi5Jvepv9h4W0oesq9VSJyGiAwZC04run5x8fhITg0nuhsdvezRN9gVWhG60VAiopthwWklJ7NLkHT5GhRyQbe/DhE1X0zDKM6GxCxU1nDKOBHdHAtOK7k+ejOimzc8ODWc6K4NDPGAv4sNVJW1+Ck5R+o4RGSgWHBaQWFpNbY2rN0xuWHZeSK6O3KZgIkNU8bXHMjglHEiuikWnFawvmFqeLifE8I5NZzonj3R0w82lnKcyy9FwqWrUschIgPEgqNnNXV/7hoew4X9iFqEo7UCY3r4AuAu40R0cyw4evb76SsoKK2Gu70Sw7pyajhRS5nUp/5jqp2p+cgq5pRxImqMBUfPrl9cPCEyAJYWfLmJWkqwhz36t3eDKAJfJ2RIHYeIDAzfcfUoOasExzNLoJAL+AenhhO1uOsf+244koXy6jppwxCRQWHB0aO1DaM3I0N94G6vlDYMkQka0MEDga42KK2qw+bjnDJORH9iwdGTgtIqbD1Zv2v4pD6B0oYhMlEymaD7/9eag5wyTkR/YsHRk+8OZ6JWI6KHvxPCODWcSG8ej/CFraUcaQVlOJDGKeNEVI8FRw/qp4ZnAuDCfkT6Zm+lwBM9/QAAaw5yl3EiqseCowe/nbqCorJqeDooMayrl9RxiEze9ZWN488W4PLVconTEJEhYMHRg9V/mRqukPMlJtK3IHc7DOjoDlEE1h7kLuNE1EoFZ+nSpQgMDISVlRUiIyORmJh42+M3bdqEkJAQWFlZoVu3bvjtt98afV8URcybNw/e3t6wtrZGdHQ0Lly4oM+n0GTHM6/hRFYJLOUyPMWp4UStZnLDxcabjmahjFPGicye3gvOxo0bMWfOHMyfPx/Hjh1DWFgYhgwZgoKCgpsef/DgQTz11FOYMmUKjh8/jtGjR2P06NE4ffq07pgPPvgAixcvxvLly3H48GHY2tpiyJAhqKqq0vfTuaPrC/uNDPOBmx2nhhO1lvvbuyPIzRal1XX48Vi21HGISGKCqOd5lZGRkejVqxc+//xzAIBWq4Wfnx9mzZqF119//Ybjx44di/LycmzdulV333333Yfw8HAsX74coijCx8cHc+fOxcsvvwwAUKlU8PT0xJo1azBu3LgbzlldXY3q6mrd12q1Gn5+flCpVHBwcGix55qvrkLf93ehTivil5n90M3XscXOTUR39nVCBub9nIIgd1vsfOkByGSC1JGIzM75/FJ8vP0cYvq2xX1Bri16brVaDUdHxya9f+t1BKempgZJSUmIjo7+8wfKZIiOjkZCQsJNH5OQkNDoeAAYMmSI7vj09HTk5eU1OsbR0RGRkZG3POfChQvh6Oiou/n5+d3rU7updYczUacV0TPAmeWGSAKP9fCFvdIClwrL8UdakdRxiMzSmoMZ2JaSr1vsVip6LThFRUXQaDTw9PRsdL+npyfy8vJu+pi8vLzbHn/9f5tzztjYWKhUKt0tKyvrrp7PnTzewxdT+7XF9PuD9HJ+Iro9O6XFn1PGD3DKOFFrU1XUYvOx+lXFpV7k1kLSn95KlEollEr9Xw/j72qDNx7urPefQ0S3NjEqAKsPpmP3uUJcKixDkLud1JGIzMb3R7NQWatBiJc9Itu6SJpFryM4bm5ukMvlyM/Pb3R/fn4+vLxuvj6Ml5fXbY+//r/NOScRmY9AN1s82NEDAPB1AqeME7UWjVbE2oQMAPUb4QqCtNfA6bXgWFpaIiIiAvHx8br7tFot4uPjERUVddPHREVFNToeAHbs2KE7vm3btvDy8mp0jFqtxuHDh295TiIyL5MbdhnfdDQLpVW10oYhMhPxqfnIvlYJJxsFRoW3kTqO/qeJz5kzB19++SXWrl2L1NRUPPfccygvL0dMTAwAYOLEiYiNjdUd/8ILLyAuLg4ff/wxzp49iwULFuDo0aOYOXMmAEAQBLz44ot49913sWXLFpw6dQoTJ06Ej48PRo8ere+nQ0RGoF+wG4I97FBeo8EPSZwyTtQaro/ejOvlDyuFXNowaIVrcMaOHYvCwkLMmzcPeXl5CA8PR1xcnO4i4czMTMhkf/asPn364LvvvsMbb7yBf/7zn2jfvj1++ukndO3aVXfMq6++ivLyckyfPh0lJSXo168f4uLiYGVlpe+nQ0RGQBDqdxl/86fTWHswA5OiAjllnEiPzueX4kDaVcgE4OmGrVOkpvd1cAxRc+bRE5FxqqipQ+R78SitqsPqyb0wMMRD6khEJuufm0/hu8OZGNrFC8ufjtDbzzGYdXCIiKRiY2mBcb3qp4yvlng9DiJT9tep4devfzMELDhEZLImRgVCEIB95wuRVlAmdRwik2RIU8P/igWHiEyWn4sNojvVX+8n9aqqRKbor1PDJ/eRfmr4X7HgEJFJi2lYTfV/x7KhquSUcaKWtOtsgUFNDf8rFhwiMmlR7VzRwdMOFTUabDqqn21aiMzVmoP1W6KM7eUHa0vpp4b/FQsOEZk0QRAwuU9bAPUrG2u0ZjdxlEgvGk0Nv88wpob/FQsOEZm80d194GitQGZxBXafLZA6DpFJuH5d2+DOXvB1tpE2zE2w4BCRyfvrlPE1vNiY6J6pKmrxo4HsGn4rLDhEZBaejgqATAD2pxXhQn6p1HGIjNqmpD+nht8XZDhTw/+KBYeIzIKvsw0Gd/YCwIX/iO7FX6eGTzKwqeF/xYJDRGbj+iqrPx7LhqqCU8aJ7sauswXIKq6Eo7UCow1savhfseAQkdmIbOuCEC97VNVqsfFoptRxiIzS9YuLx/U2vKnhf8WCQ0RmQxAExDSM4qw9yCnjRM11Ib8U+9OKDHZq+F+x4BCRWRkV3gZONgrklFRiZ2q+1HGIjMr1WYgPdfY0yKnhf8WCQ0RmxUohx1O9/QEAaw5kSBuGyIiUVNTgf8eyAUC3eKYhY8EhIrPz9H0BkMsEJFy6irN5aqnjEBmFDUeyUFWrRSdvB4OdGv5XLDhEZHZ8nKwxtEv9lHGO4hDdWZ1Gi68bPp6K6Wu4U8P/igWHiMzS9Snjm4/n4Fp5jbRhiAzctpR85Kqq4GpriUfCfKSO0yQsOERklnoGOKOLjwOq67TYcIS7jBPdzuoD9buGj4/0h5XCcKeG/xULDhGZpfpdxgMBAN8kZKBOo5U2EJGBOpldgqOXr0EhFzDBwKeG/xULDhGZrZFhPnCxtUSuqgo7znDKONHNrG64Tu3hUB94OFhJG6YZWHCIyGxZKeT4R8OUce5PRXSjAnUVtp7MBQDdIpnGggWHiMzahIYp44npxUjJVUkdh8igfHvoMmo1IiICnBHq6yR1nGZhwSEis+blaIVhXeunjK/lKA6RTlWtBusO1+/Z9kxfw1/Y7+9YcIjI7MU0/OP9U3IurpZVS5yGyDBsOZGLq+U18HG0wpAunlLHaTYWHCIyez38nRDq64gaThknAgCIoqi7uHhin0BYyI2vLhhfYiKiFtZ4yvhl1HLKOJm5w+nFSL2ihpVChnG9/KSOc1dYcIiIAIwI9YabnSXy1FXYlpIndRwiSa3aX7+w32M9fOFkYylxmrvDgkNEBEBpIcc/IusXMeP+VGTOMq9WYEdq/bpQMQ0jm8aIBYeIqMGESH9YyAQcvXwNp7I5ZZzM09qEDIgi0L+9G9p72ksd566x4BARNfBwsMKIUG8AwBpOGSczVFZdh+8bLrR/pp/xTQ3/K70WnOLiYowfPx4ODg5wcnLClClTUFZWdtvjZ82ahY4dO8La2hr+/v6YPXs2VKrGv0kJgnDDbcOGDfp8KkRkJq5fbPzLiVwUlnLKOJmXH45mobS6DkFutnigvbvUce6JXgvO+PHjkZKSgh07dmDr1q3Yt28fpk+ffsvjc3NzkZubi48++ginT5/GmjVrEBcXhylTptxw7OrVq3HlyhXdbfTo0Xp8JkRkLrr7OyPczwk1Gi2+OXRZ6jhErUarFbE2of7v/OS+gZDJBIkT3RtBFEVRHydOTU1F586dceTIEfTs2RMAEBcXh+HDhyM7Oxs+Pj5NOs+mTZswYcIElJeXw8LCoj60IGDz5s1NLjXV1dWorv7zNzG1Wg0/Pz+oVCo4ODg074kRkcnbejIXM787DhdbSxx8/UFYKeRSRyLSu11n8/HMmqOwt7LAodhBsFVaSB3pBmq1Go6Ojk16/9bbCE5CQgKcnJx05QYAoqOjIZPJcPjw4Saf5/qTuF5urpsxYwbc3NzQu3dvrFq1CrfraQsXLoSjo6Pu5udnnHP6iah1DO3ihTZO1igur8Hm4zlSxyFqFSsbpoaP6+VnkOWmufRWcPLy8uDh4dHoPgsLC7i4uCAvr2lrTBQVFeGdd9654WOtt99+G99//z127NiBMWPG4Pnnn8eSJUtueZ7Y2FioVCrdLSuLK5US0a1ZyGW6nZNX7k+HVquXgW4ig5GSq8KBtKuQywRMMuKp4X/V7Ir2+uuvY9GiRbc9JjU19a4DXadWqzFixAh07twZCxYsaPS9N998U/ff3bt3R3l5OT788EPMnj37pudSKpVQKpX3nImIzMeTvfzw6c4LSCsow94LhRjY0ePODyIyUtdHb4Z19YKvs43EaVpGswvO3LlzMXny5NseExQUBC8vLxQUFDS6v66uDsXFxfDy8rrt40tLSzF06FDY29tj8+bNUCgUtz0+MjIS77zzDqqrq1lkiKhFOFgpMLaXH1buT8eq/eksOGSy8tVV+OVELgBgav8gidO0nGYXHHd3d7i733nqWFRUFEpKSpCUlISIiAgAwK5du6DVahEZGXnLx6nVagwZMgRKpRJbtmyBlZXVHX9WcnIynJ2dWW6IqEVN7hOI1QfS8ceFIpzNUyPEi5MSyPSsPZiBWo2IXoH1MwhNhd6uwenUqROGDh2KadOmITExEQcOHMDMmTMxbtw43QyqnJwchISEIDExEUB9uRk8eDDKy8uxcuVKqNVq5OXlIS8vDxqNBgDwyy+/4KuvvsLp06eRlpaGZcuW4b333sOsWbP09VSIyEz5udhgWNf6hf9W/pEucRqilldRU4d1hzMBmNboDXAXIzjNsW7dOsycORODBg2CTCbDmDFjsHjxYt33a2trce7cOVRUVAAAjh07ppthFRwc3Ohc6enpCAwMhEKhwNKlS/HSSy9BFEUEBwfjk08+wbRp0/T5VIjITE3p3xa/nrqCn5Nz8crQjvCwv/OoMpGx+CEpG6rKWgS42iC6k6fUcVqU3tbBMWTNmUdPRPTYfw/gWGYJZj8YjDmDO0odh6hFaLQiHvx4Dy5frcDbo7pgYlSg1JHuyCDWwSEiMhXXh+6/OXQZVbUaidMQtYydqfm4fLUCjtYKPB7hK3WcFseCQ0R0B4M7e8LX2RrXKmrx4zEu/Eem4as/LgEAxkf6w8bS+Bf2+zsWHCKiO6hf+K9+Z+WV+y9x4T8yeslZJTiScQ0Kueks7Pd3LDhERE3wZE9f2CstcLGwHHvPF0odh+ieXB+9GRnmA08H07xwngWHiKgJ7K0UGNe7fh+7LxveHIiMUfa1Cvx+un7LpKn9TGtq+F+x4BARNdHkvm0hlwk4ePEqTueopI5DdFfWHMiARiuib7ArOvuY7kxiFhwioiZq42SNh0PrF/77Yh9Hccj4lFbVYsOR+g2nTW1hv79jwSEiaobp99e/Kfx6MhdZxRUSpyFqng2JWSirrkOwhx0eaH/nbZeMGQsOEVEzdPFxRP/2btCKf+7ATGQMauq0ur+z0/q3hUwmSJxIv1hwiIia6dkH2gEANhzJRHF5jcRpiJrm5+Qc5Kmr4GGvxOjubaSOo3csOEREzdSnnSu6+DigqlaLbxIuSx2H6I60WhErGq4be6ZfWygt5BIn0j8WHCKiZhIEAf/XMIqzNiGD2zeQwdt1tgAXCspgr7TAPyL9pY7TKlhwiIjuwvCuXvB1tkZxeQ02JWVLHYfotr7YdxEA8I/7/OFgpZA4TetgwSEiugsWchmm9qvfvuHLfZeg4fYNZKCSLhfjSMY1WMpleKZhyxFzwIJDRHSXnuzlBycbBTKLKxDXsDIskaFZvrf+2ptHu7cx2W0ZboYFh4joLtlYWmBiVCAAYMW+ixBFjuKQYUkrKMWOM/kQBGD6A6a9sN/fseAQEd2DSVEBUFrIcCJbhUOXiqWOQ9TI9ZlTD3XyRDt3O4nTtC4WHCKie+Bqp8QTPX0B/HkhJ5EhyFNVYfPxHADAswPaSZym9bHgEBHdo6n9giATgD3nCnE2Ty11HCIAwOoD6ajViOgd6IIe/s5Sx2l1LDhERPco0M0WQ7t6AQBW7OUmnCQ9VWUt1h3OBAA8O8C8rr25jgWHiKgFXN++4ecT3ISTpLfu8GWUVdeho6c9Bnb0kDqOJFhwiIhaQKivE/q3d4NGK2L5Xl6LQ9KpqtVg9YEMAMD0+4MgCKa9qeatsOAQEbWQGQODAQCbjmYjX10lcRoyVz8kZaOwtBrejlZ4JNxH6jiSYcEhImohkW1d0DPAGTUaLb7cx2txqPXVarRYtqd+BPH/7g+CQm6+b/Pm+8yJiFqYIAiY8WD9KM66w5koLq+ROBGZm5+Tc5FTUgk3O0uM620em2reCgsOEVELGtDBHV3bOKCyVoPVB9KljkNmRKMV8d/daQCAaf2DYKWQS5xIWiw4REQtSBAEzBhQP4qz5mAG1FW1Eicic/HbqSu4VFQOJxsFxt8XIHUcybHgEBG1sCFdvBDsYYfSqjp8k3BZ6jhkBrRaEZ/vqh+9eaZvW9gpLSROJD0WHCKiFiaTCXi+YWn8VfvTUVmjkTgRmbqdqfk4l18Ke6UFJvUJlDqOQWDBISLSg0fCfODnYo2r5TVYn5gpdRwyYaIo4vOGa28m9gmAo7VC4kSGgQWHiEgPLOQy3erGK/ZdQk2dVuJEZKr2XSjCyWwVrBVyPNO3rdRxDIZeC05xcTHGjx8PBwcHODk5YcqUKSgrK7vtYwYMGABBEBrdnn322UbHZGZmYsSIEbCxsYGHhwdeeeUV1NXV6fOpEBE12+MRvvB0UCJPXYUfj2VLHYdMkCiKWBJ/AQDwj0h/uNopJU5kOPRacMaPH4+UlBTs2LEDW7duxb59+zB9+vQ7Pm7atGm4cuWK7vbBBx/ovqfRaDBixAjU1NTg4MGDWLt2LdasWYN58+bp86kQETWb0kKOaf3rNzpctvci6jQcxaGWdTi9GEcvX4OlXIbp95vnppq3oreCk5qairi4OHz11VeIjIxEv379sGTJEmzYsAG5ubm3fayNjQ28vLx0NwcHB933tm/fjjNnzuDbb79FeHg4hg0bhnfeeQdLly5FTc3NF9Wqrq6GWq1udCMiag3/iPSHi60lLl+twNaTV6SOQybm+sypJ3v5wtPBSuI0hkVvBSchIQFOTk7o2bOn7r7o6GjIZDIcPnz4to9dt24d3Nzc0LVrV8TGxqKi4s+deRMSEtCtWzd4enrq7hsyZAjUajVSUlJuer6FCxfC0dFRd/Pz87vHZ0dE1DQ2lhaY0q/+uogluy5AoxUlTkSm4ljmNexPK4KFTMD/3d9O6jgGR28FJy8vDx4ejbdot7CwgIuLC/Ly8m75uH/84x/49ttvsXv3bsTGxuKbb77BhAkTGp33r+UGgO7rW503NjYWKpVKd8vKyrrbp0VE1GwTowLgZKPAxcJybD15+xFsoqZa2jB682j3NvBzsZE4jeFp9kpAr7/+OhYtWnTbY1JTU+860F+v0enWrRu8vb0xaNAgXLx4Ee3a3V1DVSqVUCp54RURScPeSoFp/YPw4bZz+Cz+Ah4O9YFcJkgdi4zYqWwV4s8WQCYAzw3g6M3NNLvgzJ07F5MnT77tMUFBQfDy8kJBQUGj++vq6lBcXAwvL68m/7zIyEgAQFpaGtq1awcvLy8kJiY2OiY/Px8AmnVeIqLWNKlPIL784xIuFZbjlxO5GN29jdSRyIj9Z+d5AMDo8DYIcreTOI1hanbBcXd3h7u7+x2Pi4qKQklJCZKSkhAREQEA2LVrF7Rara60NEVycjIAwNvbW3fef//73ygoKNB9BLZjxw44ODigc+fOzXw2REStw05poRvFWRx/ASPDOIpDd+d45jXsOlsAuUzArEHtpY5jsPR2DU6nTp0wdOhQTJs2DYmJiThw4ABmzpyJcePGwcfHBwCQk5ODkJAQ3YjMxYsX8c477yApKQkZGRnYsmULJk6ciPvvvx+hoaEAgMGDB6Nz5854+umnceLECWzbtg1vvPEGZsyYwY+hiMigTeoTCGcbBS4VlWPLiRyp45CR+s/O+nVvHu3eBm3dbCVOY7j0ug7OunXrEBISgkGDBmH48OHo168fVqxYoft+bW0tzp07p5slZWlpiZ07d2Lw4MEICQnB3LlzMWbMGPzyyy+6x8jlcmzduhVyuRxRUVGYMGECJk6ciLffflufT4WI6J7ZKS0wrWGtkiXxaVwXh5ot6XIx9p0vhFwmYPaDHL25HUEURbObs6hWq+Ho6AiVStVojR0iIn0rq65D/0W7cK2iFp88GYbHevhKHYmMyISvDmN/WhHG9fLD+2NCpY7T6prz/s29qIiIWpGd0gLTG9YsWbKLozjUdIcvXdWtezNjYLDUcQweCw4RUSubGBUAF1tLpBeV48djvBaHmub6zKkne/lx3ZsmYMEhImpltkoLPN+wdsmnO8+juk4jcSIydAcvFuHQpWJYymUcvWkiFhwiIglMuC8A3o5WyFVV4bvDmVLHIQMmiiI+2nYOADC2lx/aOFlLnMg4sOAQEUnASiHH7IY1TJbuTkN5dZ3EichQ7UwtwLHMElgpZJj1IEdvmooFh4hIIo9H+CLQ1QZFZTVYczBD6jhkgDTaP0dvYvq2hQd3DG8yFhwiIoko5DK89FAHAMDyvRehqqiVOBEZmi0ncnAuvxQOVhZ4ljuGNwsLDhGRhEaG+iDEyx6lVXX4Yt9FqeOQAamp0+KTHfUzp54d0A6ONgqJExkXFhwiIgnJZALmDu4IAFh9IAMFpVUSJyJDseFIJrKKK+Fhr0RMn7ZSxzE6LDhERBKL7uSBcD8nVNZqsCQ+Teo4ZAAqauqwuOHvwqxB7WFtKZc4kfFhwSEikpggCHhtaAgAYH1iJi4VlkmciKS2+kAGisqqEeBqg3G9/KSOY5RYcIiIDEBUO1c8GOKBOq2ID+LOSR2HJHStvAbL99ZfjzXnoQ5QyPlWfTf4qhERGYjXh4VAJgBxKXk4mlEsdRySyGfxF1BaVYdO3g4YGeojdRyjxYJDRGQgOnja48me9R9HvPdbKkRRlDgRtbb0onJ8e+gyAOCNEZ0gkwkSJzJeLDhERAbkpYc6wFohx7HMEsSdzpM6DrWy939PRZ1WxMCO7ugb7CZ1HKPGgkNEZEA8HawwrX/9lOBFcWdRq9FKnIhaS2J6Mbal5EMmAP8c3knqOEaPBYeIyMBMf6Ad3OwskXG1ghtxmgmtVsS/fz0DABjX2x/tPe0lTmT8WHCIiAyMndICL0TXb+HwWfwFqKu4hYOp++VkLk5kq2BrKcdLDX/2dG9YcIiIDNC4Xn5o526L4vIaLIm/IHUc0qOqWo1uaYDnBrSDu71S4kSmgQWHiMgAKeQyvPlwZwD1i75d5OJ/Jmv1gQzklFTCy8EKU/oFSR3HZLDgEBEZqAEdPXSL/7279YzUcUgP8tVV+HxX/QjdK0M6ckuGFsSCQ0RkwN4Y0QkKuYDd5wqx+2yB1HGohb3/+1mU12jQ3d8Jj3ZvI3Uck8KCQ0RkwILc7RDTt37a+Dtbz6CmjtPGTcXRjGJsPp4DQQAWjOzCRf1aGAsOEZGBm/VgMNzsLHGpqBxfJ2RIHYdagEYrYv6WFADAkxF+CPNzkjaQCWLBISIycPZWCrw6pH638c92XkBRWbXEiehebTyShZRcNeytLPDK0I5SxzFJLDhEREbg8QhfdGvjiNLqOnwQd1bqOHQPVBW1+HBb/Z/hS9Ed4GbHaeH6wIJDRGQEZDIBCx7pAgD4/mg2jnC3caP1yY5zuFZRiw6edng6KkDqOCaLBYeIyEhEBDjjqd71u43/a/Mp7lNlhFJyVfimYbfwBSO7QCHn27C+8JUlIjIirw0NgYutJc7nl2Hl/nSp41AzaLQiYn88Ba0IjAj1Rh/uFq5XLDhEREbEycZSt9P0ZzsvIPtahcSJqKm+ScjAyWwV7K0sML9hlWrSHxYcIiIjM6ZHG0S2dUFlrQYLtnCFY2NwRVWJD7fV7zf12tAQeDhYSZzI9Om14BQXF2P8+PFwcHCAk5MTpkyZgrKyW++nkpGRAUEQbnrbtGmT7ribfX/Dhg36fCpERAZDEAT8+9GuUMgF7EzNx/aUPKkj0R0s2JKC8hoNevg74R+9/aWOYxb0WnDGjx+PlJQU7NixA1u3bsW+ffswffr0Wx7v5+eHK1euNLq99dZbsLOzw7Bhwxodu3r16kbHjR49Wp9PhYjIoAR72GNa//qNGRdsSUF5dZ3EiehWtqfkYVtKPixkAhY+FsoVi1uJhb5OnJqairi4OBw5cgQ9e/YEACxZsgTDhw/HRx99BB8fnxseI5fL4eXl1ei+zZs348knn4SdnV2j+52cnG449laqq6tRXf3nwlhqtbq5T4eIyODMerA9fjmZi6ziSiyKO4u3R3WVOhL9TVl1nW7F4un3B6Gjl73EicyH3kZwEhIS4OTkpCs3ABAdHQ2ZTIbDhw836RxJSUlITk7GlClTbvjejBkz4Obmht69e2PVqlUQRfGW51m4cCEcHR11Nz8/v+Y/ISIiA2NtKcf7j4UCAL5OuIyEi1clTkR/99G2c7iiqoK/iw1mD2ovdRyzoreCk5eXBw8Pj0b3WVhYwMXFBXl5Tfu8eOXKlejUqRP69OnT6P63334b33//PXbs2IExY8bg+eefx5IlS255ntjYWKhUKt0tKyur+U+IiMgA9Q12w1MN13S89r+TqKjhR1WGIuHiVaw5mAEA+PejXWGlkEsbyMw0u+C8/vrrt7wQ+Prt7Nl7X0a8srIS33333U1Hb95880307dsX3bt3x2uvvYZXX30VH3744S3PpVQq4eDg0OhGRGQq/jk8BD6OVsgsrtDN1CFplVfX4ZUfTgAAnurtj/7t3SVOZH6aXXDmzp2L1NTU296CgoLg5eWFgoKCRo+tq6tDcXFxk66d+eGHH1BRUYGJEyfe8djIyEhkZ2c3us6GiMhc2FspsHBM/UdVaw5mcBsHA/Deb6nIvlaJNk7W+NeITlLHMUvNvsjY3d0d7u53bqJRUVEoKSlBUlISIiIiAAC7du2CVqtFZGTkHR+/cuVKPPLII036WcnJyXB2doZSyQ3LiMg8PdDBHU/29MX3R7Px6g8n8dvs/rC25EciUvjjQiHWHc4EAHz4eCjslHqbz0O3obdrcDp16oShQ4di2rRpSExMxIEDBzBz5kyMGzdON4MqJycHISEhSExMbPTYtLQ07Nu3D1OnTr3hvL/88gu++uornD59GmlpaVi2bBnee+89zJo1S19PhYjIKPxrRGd4OiiRXlSOj7bzoyopqKtq8doPJwEAE6MCuB2DhPS6Ds66desQEhKCQYMGYfjw4ejXrx9WrFih+35tbS3OnTuHiorGS42vWrUKvr6+GDx48A3nVCgUWLp0KaKiohAeHo4vvvgCn3zyCebPn6/Pp0JEZPAcrRW6WVUr96fjjwuFEicyP+9uPYPchllTrw8LkTqOWRPE282vNlFqtRqOjo5QqVS84JiITM6bP53GN4cuw91eibgX+sPVjh/ft4btKXmY/k0SBAHYOD0Kvdu6SB3J5DTn/Zt7URERmZh/jeiE9h52KCytxmv/O3nbdcKoZeSWVOKVho+mpvZry3JjAFhwiIhMjJVCjsVPdYelXIadqQX49tBlqSOZtDqNFi9sOA5VZS1CfR3xyhB+NGUIWHCIiExQJ28HvNZwDci7v6bifH6pxIlM1+JdaTiScQ12Sgsseao7LC341moI+KdARGSiYvoE4oEO7qiu02L2+uOoqtVIHcnkHLp0FZ/vugCgfrXiAFdbiRPRdSw4REQmSiYT8NETYXC1tcTZvFLM+/k0r8dpQdfKa/DihmRoReDxCF+MCm8jdST6CxYcIiIT5m6vxGfjukMmAN8fzcaGI9yLryVotCLmfJ+MPHUVgtxt8dYjXaSORH/DgkNEZOL6tXfD3MEdAQDzf05BclaJtIFMwH92nMfuc4VQWsiw5KnusOVqxQaHBYeIyAw8P6AdBnf2RI1Gi+e/TcLVMu7dd7d+O3UFn+9OAwAsGhOKLj6OEieim2HBISIyA4Ig4KMnwxDkZotcVRVmrT+OOo1W6lhG52yeGi9vqt8lfGq/thjdndfdGCoWHCIiM+FgpcDypyNgYynHwYtXsSjurNSRjEpJRQ2mf52EihoN+ga7cisGA8eCQ0RkRjp42uODx+v3q/ryj3SsO8xFAJuiTqPFrPXHkVlcAV9na3z+VA9YyPkWasj4p0NEZGYeDvXBi9HtAdTvW7X7bIHEiQybKIp48+cU/HGhCNYKOVY83RPOtpZSx6I7YMEhIjJDLwxqj8cjfKEVgRnfHcPpHJXUkQzW4vg0rE/MhCAA/xkbjs4+3KTZGLDgEBGZIUEQ8N6j3dA32BUVNRrErDmCnJJKqWMZnA2JmfjPzvMAgLdHdcXQrl4SJ6KmYsEhIjJTlhYyLJsQgY6e9igsrUbM6kSoKmqljmUwdp7Jxz83nwIAzBwYjKfvC5A4ETUHCw4RkRlzsFJgVUwveNgrcT6/DBNXHYa6iiUn6fI1zFx/DFoReCLCF3MHd5A6EjUTCw4RkZlr42SNr6f0hrONAieyVZi0KhGlZlxyjmdew+TViaiq1WJgR3e891g3CIIgdSxqJhYcIiJCiJcDvp0aCUdrBY5nliBm9RGUV9dJHavVJV0uxtMrE1FaVYfegS5YOr4HFJwObpT4p0ZERACALj6OWDc1Eg5WFjh6+Rpi1hxBRY35lJwjGcWYuDIRZdV1uC/IBWue6QUbS+4xZaxYcIiISKdrG0d8MyUS9koLJKYXY/LqI2ZxTc6hS1cxaVUiyhtWKV49uTfLjZFjwSEiokbC/JywdkpvXckZ98UhFJaa7uacu88WIGb1EVTUaNC/vRtWTuoFa0u51LHoHrHgEBHRDXr4O2P99PvgZmeJM1fUeHz5QVwsLJM6VovbkJiJqV8fRWWtBg90cMeXE3vCSsFyYwpYcIiI6Ka6tnHED8/2gZ+LNS5frcBj/z2IgxeLpI7VIjRaEYvizuL1H09BoxXxWI82LDcmhgWHiIhuKdDNFpuf74vu/k5QVdZi4spEfJ2QAVEUpY5219RVtZj29VEs23MRQP0ifh8/EQZLC74lmhL+aRIR0W252Smxftp9GBnmgzqtiHk/p2DO9yeMcoZVSq4Koz8/gF1nC6C0kOHTseF4eUhHrnNjglhwiIjojqwUciweF443RnSCXCZg8/EcjFyy32g26RRFEd8kZODR/x7EpaJyeDtaYdOzURjdvY3U0UhPBNGYxxnvklqthqOjI1QqFRwcuCssEVFzHLp0FbPXH0dBaTUUcgEvRnfA9PuDDHZBvCuqSrz2v1PYd74QADAoxAMfPREGZ1tLiZNRczXn/ZsFhwWHiKjZrpXX4PUfT2JbSj4AoJO3AxaN6YZQXydpg/2FRiviu8OX8cG2cyitqoOlhQyvDumIKf3a8iMpI8WCcwcsOERE904URfzvWA7e2XoGqspaCALwZIQf5g7pAA97K0mzJaYX4+2tKTidowZQv7bPx0+EIdjDTtJcdG9YcO6ABYeIqOUUlVXjna1n8HNyLgDA1lKOyX0DMbVfUKt/DHQ6R4WPt5/D7nP1H0fZW1nglSEdMT4yAHIZR22MHQvOHbDgEBG1vKTLxXh7aypOZJUAqC86Y3v54+moALR1s9Xbz9VqRexPK8KXf1zCHxfq1+mRywQ82dMPcx7qAHd7pd5+NrWu5rx/6+2KsH//+9/o06cPbGxs4OTk1KTHiKKIefPmwdvbG9bW1oiOjsaFCxcaHVNcXIzx48fDwcEBTk5OmDJlCsrKTG91TSIiYxMR4ILNz/XBF09HoIuPA8prNFh1IB0DP9qDCV8dxvdHs1p0X6u0gjJ8tvMC7v9wNyauSsQfF4ogE4BHwnyw46X7sfCxbiw3ZkxvIzjz58+Hk5MTsrOzsXLlSpSUlNzxMYsWLcLChQuxdu1atG3bFm+++SZOnTqFM2fOwMqq/vPcYcOG4cqVK/jiiy9QW1uLmJgY9OrVC999912Ts3EEh4hIv0RRxN7zhVh7MAN7zhfi+juNQi6gh78z7u/gju7+TujaxhEOVoomnS9XVYXkzBIcySjGvguFuFRYrvu+vdICYyJ8MaVfW/i52OjraZHEDOojqjVr1uDFF1+8Y8ERRRE+Pj6YO3cuXn75ZQCASqWCp6cn1qxZg3HjxiE1NRWdO3fGkSNH0LNnTwBAXFwchg8fjuzsbPj4+Nz03NXV1aiu/nOjOLVaDT8/PxYcIqJWkHm1AltO5OCn5FykFdw44u7poISfsw08HJSwVypgpZChTiuiuk6L4vIaFJRWIb2wHOU1mkaPU8gFRLVzw+hwHwzr6s0NMs1AcwqOwewFn56ejry8PERHR+vuc3R0RGRkJBISEjBu3DgkJCTAyclJV24AIDo6GjKZDIcPH8ajjz5603MvXLgQb731lt6fAxER3cjf1QYzH2yPmQ+2R0ZROf64UIiES1dxMluF7GuVyFdXI199593KLWQC2nvao3egM3q3dcX9Hdxg34TRHzJPBlNw8vLyAACenp6N7vf09NR9Ly8vDx4eHo2+b2FhARcXF90xNxMbG4s5c+bovr4+gkNERK0r0M0WgW62eDoqEABQUlGDy1crkFlcgeLyGpRV16GqVgO5TIBCLoOrrSXc7JQIcLVBoJutwS4mSIanWQXn9ddfx6JFi257TGpqKkJCQu4pVEtTKpVQKnmhGRGRoXGysYSTjSXC/JykjkImplkFZ+7cuZg8efJtjwkKCrqrIF5eXgCA/Px8eHt76+7Pz89HeHi47piCgoJGj6urq0NxcbHu8URERETNKjju7u5wd3fXS5C2bdvCy8sL8fHxukKjVqtx+PBhPPfccwCAqKgolJSUICkpCREREQCAXbt2QavVIjIyUi+5iIiIyPjo7cPMzMxMJCcnIzMzExqNBsnJyUhOTm60Zk1ISAg2b94MABAEAS+++CLeffddbNmyBadOncLEiRPh4+OD0aNHAwA6deqEoUOHYtq0aUhMTMSBAwcwc+ZMjBs37pYzqIiIiMj86O0i43nz5mHt2rW6r7t37w4A2L17NwYMGAAAOHfuHFQqle6YV199FeXl5Zg+fTpKSkrQr18/xMXF6dbAAYB169Zh5syZGDRoEGQyGcaMGYPFixfr62kQERGREeJWDVwHh4iIyCgYxFYNRERERFJhwSEiIiKTw4JDREREJocFh4iIiEwOCw4RERGZHBYcIiIiMjksOERERGRyWHCIiIjI5OhtJWNDdn1tQ7VaLXESIiIiaqrr79tNWaPYLAtOaWkpAMDPz0/iJERERNRcpaWlcHR0vO0xZrlVg1arRW5uLuzt7SEIQoueW61Ww8/PD1lZWdwG4m/42tweX5/b4+tze3x9bo2vze0Z0+sjiiJKS0vh4+MDmez2V9mY5QiOTCaDr6+vXn+Gg4ODwf9FkQpfm9vj63N7fH1uj6/PrfG1uT1jeX3uNHJzHS8yJiIiIpPDgkNEREQmhwWnhSmVSsyfPx9KpVLqKAaHr83t8fW5Pb4+t8fX59b42tyeqb4+ZnmRMREREZk2juAQERGRyWHBISIiIpPDgkNEREQmhwWHiIiITA4LDhEREZkcFpwWtHTpUgQGBsLKygqRkZFITEyUOpLB2LdvH0aOHAkfHx8IgoCffvpJ6kgGY+HChejVqxfs7e3h4eGB0aNH49y5c1LHMhjLli1DaGiobpXVqKgo/P7771LHMkjvv/8+BEHAiy++KHUUg7BgwQIIgtDoFhISInUsg5KTk4MJEybA1dUV1tbW6NatG44ePSp1rBbBgtNCNm7ciDlz5mD+/Pk4duwYwsLCMGTIEBQUFEgdzSCUl5cjLCwMS5culTqKwdm7dy9mzJiBQ4cOYceOHaitrcXgwYNRXl4udTSD4Ovri/fffx9JSUk4evQoHnzwQYwaNQopKSlSRzMoR44cwRdffIHQ0FCpoxiULl264MqVK7rb/v37pY5kMK5du4a+fftCoVDg999/x5kzZ/Dxxx/D2dlZ6mgtQ6QW0bt3b3HGjBm6rzUajejj4yMuXLhQwlSGCYC4efNmqWMYrIKCAhGAuHfvXqmjGCxnZ2fxq6++kjqGwSgtLRXbt28v7tixQ3zggQfEF154QepIBmH+/PliWFiY1DEM1muvvSb269dP6hh6wxGcFlBTU4OkpCRER0fr7pPJZIiOjkZCQoKEycgYqVQqAICLi4vESQyPRqPBhg0bUF5ejqioKKnjGIwZM2ZgxIgRjf4NonoXLlyAj48PgoKCMH78eGRmZkodyWBs2bIFPXv2xBNPPAEPDw90794dX375pdSxWgwLTgsoKiqCRqOBp6dno/s9PT2Rl5cnUSoyRlqtFi+++CL69u2Lrl27Sh3HYJw6dQp2dnZQKpV49tlnsXnzZnTu3FnqWAZhw4YNOHbsGBYuXCh1FIMTGRmJNWvWIC4uDsuWLUN6ejr69++P0tJSqaMZhEuXLmHZsmVo3749tm3bhueeew6zZ8/G2rVrpY7WIiykDkBEf5oxYwZOnz7N6wT+pmPHjkhOToZKpcIPP/yASZMmYe/evWZfcrKysvDCCy9gx44dsLKykjqOwRk2bJjuv0NDQxEZGYmAgAB8//33mDJlioTJDINWq0XPnj3x3nvvAQC6d++O06dPY/ny5Zg0aZLE6e4dR3BagJubG+RyOfLz8xvdn5+fDy8vL4lSkbGZOXMmtm7dit27d8PX11fqOAbF0tISwcHBiIiIwMKFCxEWFobPPvtM6liSS0pKQkFBAXr06AELCwtYWFhg7969WLx4MSwsLKDRaKSOaFCcnJzQoUMHpKWlSR3FIHh7e9/wS0KnTp1M5mM8FpwWYGlpiYiICMTHx+vu02q1iI+P53UCdEeiKGLmzJnYvHkzdu3ahbZt20odyeBptVpUV1dLHUNygwYNwqlTp5CcnKy79ezZE+PHj0dycjLkcrnUEQ1KWVkZLl68CG9vb6mjGIS+ffvesCTF+fPnERAQIFGilsWPqFrInDlzMGnSJPTs2RO9e/fGp59+ivLycsTExEgdzSCUlZU1+q0pPT0dycnJcHFxgb+/v4TJpDdjxgx89913+Pnnn2Fvb6+7bsvR0RHW1tYSp5NebGwshg0bBn9/f5SWluK7777Dnj17sG3bNqmjSc7e3v6Ga7VsbW3h6urKa7gAvPzyyxg5ciQCAgKQm5uL+fPnQy6X46mnnpI6mkF46aWX0KdPH7z33nt48sknkZiYiBUrVmDFihVSR2sZUk/jMiVLliwR/f39RUtLS7F3797ioUOHpI5kMHbv3i0CuOE2adIkqaNJ7mavCwBx9erVUkczCM8884wYEBAgWlpaiu7u7uKgQYPE7du3Sx3LYHGa+J/Gjh0rent7i5aWlmKbNm3EsWPHimlpaVLHMii//PKL2LVrV1GpVIohISHiihUrpI7UYgRRFEWJuhURERGRXvAaHCIiIjI5LDhERERkclhwiIiIyOSw4BAREZHJYcEhIiIik8OCQ0RERCaHBYeIiIhMDgsOERERmRwWHCIiIjI5LDhERERkclhwiIiIyOT8P9eOwqVymCCFAAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"plt.plot(x, s)\n",
|
||
"plt.title(\"Sinus Plot\") # Titel Setzen\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "6d0a0200-ac39-467c-a3e8-66e6a3ba3818",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-8d7bed3592e18530",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Legende und Labels\n",
|
||
"\n",
|
||
"Um eine Legende in einem Plot anzuzeigen, wird die Funktion [plt.legend](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.legend.html) **vor** dem Aufruf von `plt.show()` verwendet. \n",
|
||
"\n",
|
||
"Damit die Legende korrekt dargestellt wird, muss jeder Plot beim Aufruf von `plt.plot` mit dem Parameter `label` versehen werden, der einen beschreibenden String enthält. \n",
|
||
"\n",
|
||
"Im Folgenden plotten wir den Sinus und Kosinus mit entsprechenden Labels, sodass die Legende die beiden Funktionen eindeutig unterscheidet."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 35,
|
||
"id": "4d58a327-a11e-408b-a998-ef03c7cfaf87",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-b1d037b9a275622c",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAhcdJREFUeJzt3XdcleX/x/HXOYe9QRBEQNy4cSLuQY7MtKy0LEeOMm3Z9PurbH2znWmmlbO0bGpm3yxzDxQX7i2IiiyRLeuc8/vjBpRyAHK4z/g8H4/z4PZwn3PeB63z4bqv63NpjEajESGEEEIIK6JVO4AQQgghRHWTAkcIIYQQVkcKHCGEEEJYHSlwhBBCCGF1pMARQgghhNWRAkcIIYQQVkcKHCGEEEJYHSlwhBBCCGF17NQOoAaDwUBiYiLu7u5oNBq14wghhBCiAoxGI9nZ2QQGBqLV3nyMxiYLnMTERIKDg9WOIYQQQogqOHfuHEFBQTc9xyYLHHd3d0D5AXl4eKicRgghhBAVkZWVRXBwcNnn+M3YZIFTelnKw8NDChwhhBDCwlRkeolMMhZCCCGE1ZECRwghhBBWRwocIYQQQlgdKXCEEEIIYXWkwBFCCCGE1ZECRwghhBBWRwocIYQQQlgdKXCEEEIIYXWkwBFCCCGE1TFpgbN582YGDx5MYGAgGo2GlStX3vIxGzdupF27djg6OtKoUSMWL178r3PmzJlDaGgoTk5OREREEBMTU/3hhRBCCGGxTFrg5Obm0qZNG+bMmVOh8+Pi4hg0aBC9e/cmNjaWZ555hvHjx/Pnn3+WnfP9998zdepUpk+fzt69e2nTpg39+/cnJSXFVG9DCCGEEBZGYzQajTXyQhoNK1asYOjQoTc856WXXuL333/n0KFDZfeNGDGCjIwM1qxZA0BERAQdO3bks88+A8BgMBAcHMyTTz7Jyy+/XKEsWVlZeHp6kpmZKXtRCSGEEBaiMp/fZrXZZnR0NFFRUeXu69+/P8888wwAhYWF7Nmzh2nTppV9X6vVEhUVRXR09A2ft6CggIKCgrI/Z2VlVW/wUudi4OBPYO8E9i7g7AMegeBdD3ybgJ2jaV5XVElBsZ64tFziUnNJzSkgLaeQgmI9xXoj9jot7k52eLnYE+TtQj0fF0J8XNBqb73BmxBC2AyDHtLPQHocZJ2H3DQoyoOiKxAcAS3vVS2aWRU4SUlJ+Pv7l7vP39+frKwsrly5wuXLl9Hr9dc959ixYzd83hkzZvDGG2+YJHM5yYcg5ovrf09rB37NoF4XqN8DGvQEx1tv9y6qT25BMVtOprLjTDoxcekcT85Gb6j4AKabox0tAj3oVN+HHk38CA/2wl4n8/SFEDakuBDOboO4zRC/FZIOQvGVG5xbIAWOqU2bNo2pU6eW/TkrK4vg4ODqf6GANtD9eSjOh8JcyEuDrES4dAryMyH5oHKL+QJ0jtAoCloNg7C7ZHTHRAqK9fx9JIUV+86z+WQahcWGct93d7SjQW03Ajwc8XVzxNleh51OS5HeQHZ+EZdyCjl3OY+zl/LIKShmZ1w6O+PSmb3+FF4u9tzZqg5Dw+vSMdQbjUZGd4QQVshggLhNcOAHOP678nl2LTtn8G0EHkHgVhscXMHOCYI6qJO3NJaqr/4PAQEBJCcnl7svOTkZDw8PnJ2d0el06HS6654TEBBww+d1dHTE0bEGCoig9srtn4xGyDwPiXshbgucXqcM6R3/Xbm5+ELbhyHicfCoY/qcNiAlK59F2+NZHpPA5byisvtDfFzo1dSPTvV9aBfiTR1PpwoVJsV6A6dTc4k9d5ktJ9PYeiqNjLwivt2ZwLc7E2hc241RXUK5r10Qzg46U741IYSoGQXZsGcJ7JoPl+Ou3u9aGxr1hdDuENwJfBqA1vz+v2dWBU5kZCT/+9//yt23du1aIiMjAXBwcKB9+/asW7eubLKywWBg3bp1TJkypabjVpxGA17Byq35EKXgST4Mh1dA7DLIvgjbZsKOzyF8JHR/TjlXVFpSZj6z1p/kp93nKdQrozX+Ho4MaxfEkPC6NPF3q9JIi51OS9MAd5oGuDO8YwjFegPRZy6xKjaR3w9e5GRKDq+uPMSnf59gYo8GPNy5Hi4OZvWflxBCVEx+JkR/DjvnQX6Gcp+jB7S6H1oOg5DOZlnQ/JNJV1Hl5ORw6tQpANq2bcvHH39M79698fHxISQkhGnTpnHhwgW+/vprQFkm3rJlSyZPnsyjjz7K+vXreeqpp/j999/p378/oCwTHz16NF988QWdOnVi5syZ/PDDDxw7duxfc3NuxKxWUemL4cQa2D4bzu1Q7tM5QudJ0H0qOHmqm89CZOcX8dmGUyzeFk9ByWWodiFeTOzRkKhmtbEz4VyZzCtF/LznPAu3xXH+snItura7Iy/0b8qwdkEyMVkIYRn0RbB7IWx6D/IuKffVagRdnlSKGwdXdfNRuc9vkxY4GzdupHfv3v+6f/To0SxevJgxY8YQHx/Pxo0byz3m2Wef5ciRIwQFBfHqq68yZsyYco//7LPP+OCDD0hKSiI8PJxZs2YRERFR4VxmVeBc6+x2WP+2MoELlGHAATOUilnmd1yX0WjktwMXeXv1EVKylZVyHep580L/pkQ0qFWjWYr0Blbsu8Ds9Sc5l64UOq2DPHnnnla0rCuFqhDCjJ2NhtXPQupR5c++TaD3f6DZ3WY1WmM2BY65MtsCB5TLVyf+hL/+T5mcDNCwLwz5TFlyLsokZ+Xz8s8H2HA8FYB6tVx4dVBz+jarreqE34JiPYu3xfPZ+lNkFxSj02oY360+z97RBCd78/kfhRBCUJADf70CexYpf3apBX1egbajQGd+l9mlwLkFsy5wShUXwLZPYfOHoC9QLlUN+hha3ad2MrPw2/5E/m/FQbLyi3HQaZnSpxETezQwqwIiJTufN347wu8HLgLQ1N+dTx8MJyzATP/NCSFsS8JOWDERLscrf243CqLeABcfVWPdjBQ4t2ARBU6ptJPwy0RlBRYoq63u/BDsndXNpZL8Ij1v/HaY72LOAcoloI/ub0Njf/PtKbT2SDLTfjlAWk4hDjotr9zVjEc615Nl5UIIdRgMysKW9W+B0QCewTD0c6VHm5mTAucWLKrAAWXi1+YPYfP7yj9G/5bwwNdQq6HayWrUufQ8Jny9m2NJ2Wg08GTvRjzVt7FJJxBXl7ScAl766QDrjil7pg0ND+Sde1vJSishRM26chl+eQxOluzx2Ho43PmBxSxokQLnFiyuwCl1ZhP8PA5yU8HJSylyGvRUO1WN2H4qjSe+3UtGXhG+bo58OiKcro181Y5VKUajkQVb45jxxzH0BiPN6niwYHQHAr1sczROCFHD0k7Bd8OV+Z06R6WwaTfKohaxVObz2/x/9RVXNegJj22Buh2U3gTf3KMs6bNy3+9K4JGFMWTkFdEmyJPVT3azuOIGlA1nx3dvwLLxEfi6OXD0YhZD5mxj/7kMtaMJIazdmU0wv49S3HgEwfi10H60RRU3lSUFjqXxqANjfodWD4BRryzrW/+2svrKyhiNRj5ee4KXfj6I3mBkaHgg3z8WSYCnk9rRbkvnBrVYObkrTf3dSc0uYPiX0WwouXQlhBDV7uBPsHSY0sAvqBNM3AB12qidyuSkwLFE9k5w75fQq2RX9c0fwG9PKbu6Wgm9wch/Vhxi1rqTADzVpxGfDA83q1VStyPI24WfJkXSs4kf+UUGJny9m5X7LqgdSwhhbXbMU6Y2GIqgxT0w+jdlvygbIAWOpdJooNfLcNdM0Ghh79fw62SrKHKK9Aam/hDLdzEJaDXwzj2tmNqvqdWtOnJ3smf+6A4MDQ+k2GDkme9j+XZngtqxhBDWYvtsWPOSchzxOAxbqPyCbCOkwLF0HcbCfYtAo4P931l8kVOsN/Dkt/v4NTYRO62GWQ+25aGIELVjmYy9TsvHD4QzpksoAP9ZcZAfdp1TN5QQwvJt/0xp4AfQ8yUY8C5obesjX9aoWoMWQ5WvPz2qFDlolM7HZtReuyIMBiPP/7ifNYeTcNBpmftwO/o2q9j+YpZMq9UwfXBzNBpYtC2el345gFar4b72QWpHE0JYou2fKd3wAXq+DL2nqZtHJbZVzlmzFkPhvoUlIznfwq9TLGokx2g08sqvh1hZMnLz+UjbKG5KaTQaXrurOaMi62E0wgs/7Zc5OUKIyitX3Lxks8UNSIFjXVoMhfsWXC1yVj9rEaurjEYj//39KN/uTECjgY+HhxPV3HaKm1IajYY37m7BQxEhGI0w9YdYftufqHYsIYSl2DW/fHHTy3aLG5ACx/q0uKekyNHC3iVKB2QzN/Pvk8zfGgfAe/e25u42trupqEaj4e0hLRneIRiDEZ79PpZtp9LUjiWEMHfHfof/vaAcd39eKW6sbGFGZUmBY41a3KN0qATY8DbsW6Zunpv4ZsdZPi1ZCj59cHMe6BisciL1abUaZtzbisFtlNVVj3+zh+NJ2WrHEkKYq3O74KdxylY+7UYru4HbeHEDUuBYr47joduzyvFvT8GpdermuY5NJ1J5fdVhAJ6NasLYrvVVTmQ+tFoNH97fmk6hPmQXFDN2UQzJWflqxxJCmJtLp5XtF4qvQON+MOhjKW5KSIFjzfq8pnQ8NhTDD6Pg4gG1E5U5kZzNlGV70RuMDGsXxFN9G6kdyew42un44pH2NPB1JTEzn3FLdpFbUKx2LCGEuchJVToU512CwLZKyxCdLI4uJQWONdNqYcgcqN8DCnNg2f2Qqf7KnEs5BTy6eBfZBcV0CvXhnXtbWl0Tv+ri7erA4rGdqOXqwKELWUz5di/FeoPasYQQaivKh+9GwOU48KoHD/0Ajm5qpzIrUuBYOzsHGL4UajeHnCRlJKe4QLU4+UV6Jn6zh/OXr1CvlgvzHmmPo51l9eupaSG1XJg/ugOOdlo2HE9lxh/H1I4khFCT0Qi/PwcXdoOzNzz8s81sv1AZUuDYAidPGPEtOHkp/0GUzrSvYUajkf/8cpA9Zy/j4WTHgtEd8XF1UCWLpWkb4s3M4eEALNgaxypZPi6E7dq9AGKXKqtl71sEvo3VTmSWpMCxFT71YdgCQKMsH9+zuMYjLN2ZwC/7LqDTapj7cHsa1Zbh1MoY2KoOk3o1BOClnw5wIllWVglhcxJ2wB8vK8d9p0PD3urmMWNS4NiSxlHK8kFQRnHO766xl95/LoO3fjsCwMsDwujayLfGXtuaPN+vKd0a+XKlSM9j3+whK79I7UhCiJqSdVGZZmAoguZDoevTaicya1Lg2Jruz0GzwaAvhO8fgZwUk79kRl4hTyzbS6HeQL/m/ozvLsvBq0pXsgFpXS9n4tJyee6H/RgM5t+tWghxm4oL4cfRkJMMfs2UBSSyOOOmpMCxNRoNDJ0Lvk0hO1HZoNOEe1YZDEam/rCfCxnKpOIP7m8jK6Zuk4+rA5+PbIeDTsvaI8nM3XRa7UhCCFNb+xqc2wmOnjBimayYqgApcGyRo7vyH4i9K8Rvga2fmOyl5m46zfpjKTjYafl8ZDs8ne1N9lq2pE2wF28OaQHAR38dZ1d8usqJhBAmc+JP2DlXOb73C6jVUN08FkIKHFvl2/ia7RzeUVp9V7MdZy7x0V/HAXhrSAtaBHpW+2vYshGdQhjWLgiDEZ5ZHkvmFZmPI4TVyU6ClZOU44jHoelAdfNYEClwbFn4Q9DyPjDq4edxkJ9ZbU+deaWIqd/HYjDCve3q8kAH2WPKFN4Y0oJ6tVy4kHGFV1YewmgBu8cLISrIYIAVjymdiv1bQdQbaieyKFLg2DKNBu76GLxCIOMsrJ6qNJCqBtN/PURiZj4hPi68OUQ6FZuKm6MdM4eHo9Nq+G1/Ir/sVb9TtRCimkTPhjMbwc4Z7lsA9k5qJ7IoUuDYOidPGLYQNDo49BPs/+62n3LV/kRWxiai1cAnw8Nxc5S9UUypbYg3z0Ypjb5e+/UQ8Wm5KicSQty2C3tg3ZvK8cB3wa+punkskBQ4AoI7Qu//KMe/Pw/pZ6r8VIkZV3hlxUEApvRpTPt63tWRUNzCpF6N6FTfh9xCPU9/H0uR7FclhOUqzIWfxysbJTcfAu1Gq53IIkmBIxTdnoXQ7lCUC79OUa79VpLBYOS5H/aTlV9MmyBPnuwjO4TXFJ1Ww8zh4Xg42bH/XAaz151UO5IQoqr+fkP5RdOjLgz+VPrdVJEUOEKh1cGQz5Sl42e3QcyXlX6KhdviiD5zCWd7HZ8MD8deJ/+8alKglzP/vacVAJ9vPM3hxOqbNC6EqCHxWyHmC+X47tnKZpqiSmrkE2jOnDmEhobi5OREREQEMTExNzy3V69eaDSaf90GDRpUds6YMWP+9f0BAwbUxFuxbt6h0K/kmu/fr8OlijeQO52aw/t/KkvCX72rOQ38pAmVGga3CWRgywCKDUae//GAXKoSwpIU5sKvk5XjdqOhUV9181g4kxc433//PVOnTmX69Ons3buXNm3a0L9/f1JSrr9FwC+//MLFixfLbocOHUKn03H//feXO2/AgAHlzvvuu9ufHCuA9o9C/R5QfKXCl6oMBiMv/XSAwmIDPZr48WAnWRKupjeHtMTbxZ6jF7P4fIN0ORbCYvz9BlyOB89g6Pe22mksnskLnI8//pgJEyYwduxYmjdvzrx583BxcWHhwoXXPd/Hx4eAgICy29q1a3FxcflXgePo6FjuPG9vGcarFlot3F1yqSphe4UuVS3deZbdZy/j6qDjnXtkSbja/Nwdef1upcvxZxtOciwpS+VEQohbKndpahY4eaibxwqYtMApLCxkz549REVFXX1BrZaoqCiio6Mr9BwLFixgxIgRuLq6lrt/48aN1K5dm6ZNmzJp0iQuXbp0w+coKCggKyur3E3chHe9Cl+qOn85j/f+OAbASwPDCPJ2qYGA4lbubhPIHc39KdIbef7H/XKpSghz9s9LUw37qJvHSpi0wElLS0Ov1+Pv71/ufn9/f5KSkm75+JiYGA4dOsT48ePL3T9gwAC+/vpr1q1bx3vvvcemTZsYOHAgev31N42cMWMGnp6eZbfgYLmEckvXXqpa9eR1GwAajUb+b8Uhcgv1dKjnzcMR9VQIKq5Ho9Hw36Et8XS259CFLL7cXPWl/0IIE1v3llyaMgGzXuayYMECWrVqRadOncrdP2LECO6++25atWrF0KFDWb16Nbt27WLjxo3XfZ5p06aRmZlZdjt37lwNpLdwZZeqXJRVVbHL/nXKin0X2HQiFQc7Le/d1xqtVi5NmZPaHk68dldzAD79+ySnU3NUTiSE+JfEfVcvTQ2eKZemqpFJCxxfX190Oh3Jycnl7k9OTiYgIOCmj83NzWX58uWMGzfulq/ToEEDfH19OXXq1HW/7+joiIeHR7mbqADvetDrZeX4r1ch9+plwNTsAt5cfQSAZ6Ia01BWTZmle9vVpWcTPwr1Bl6VvaqEMC8GPfz2DBgNyr6AjaJu+RBRcSYtcBwcHGjfvj3r1q0ru89gMLBu3ToiIyNv+tgff/yRgoICHn744Vu+zvnz57l06RJ16tS57cziHzo/Af4t4Uo6rH217O7//n6EjLwiWgR6MKF7AxUDipvRaDS8NaQljnZatp++xKr9iWpHEkKUivkKLsYqW+b0f0ftNFbH5Jeopk6dyldffcWSJUs4evQokyZNIjc3l7FjxwIwatQopk2b9q/HLViwgKFDh1KrVq1y9+fk5PDCCy+wY8cO4uPjWbduHUOGDKFRo0b079/f1G/H9ujs4a6ZgEa5TBW3he2n01gZm4hGAzPubSUN/cxcSC2Xsq7Sb60+QmZekcqJhBBkXoD1bynHUa+Du/9NTxeVZ/JPpuHDh/Phhx/y2muvER4eTmxsLGvWrCmbeJyQkMDFixfLPeb48eNs3br1upendDodBw4c4O6776ZJkyaMGzeO9u3bs2XLFhwdHU39dmxTcEfooBSkxtXP8tbKWABGRoTQOshLvVyiwib0aEBDP1fScgr54K9jascRQqx5CQpzIKgTtBujdhqrpDHa4EX5rKwsPD09yczMlPk4FXUlAz7rCLkpfFR0H986jWD9c73wdLFXO5mooOjTl3jwqx1oNLDiia6EB3upHUkI23R8DXw3HDQ6eGwzBLRUO5HFqMznt1xbEBXj7MXl7m8AMMXuV97u6SLFjYWJbFiLe9vVxWiE/1txkGLpjSNEzSvMg/+9oBxHTpbixoSkwBEVNu1EEzbrW+GoKWLA+U/VjiOq4D93NsPT2Z7DiVl8HX1W7ThC2J6tn0BmgtLzpnSVqjAJKXBEhWw8nsKaI8m8pR+NUWuH5sSfcPJvtWOJSvJ1c+SlAWEAfPL3CS7lFKicSAgbcvksbJ+lHPf/Lzi43vx8cVukwBG3VFCs5/VVhwHo2aUrmojHlW+seRmKC1VMJqpieMdgWgR6kJ1fzId/nVA7jhC2469XoDhf6RLf7G6101g9KXDELS3eFk/8pTxquzvyzB1NoOeL4OoHl05e7cApLIZOq2H6YGUzzuW7EjicmKlyIiFswJlNcHSVMrF4wHsgmxKbnBQ44qZSswuYvV7pEP3igDDcHO2UplR9pysnbHwPspNv8gzCHHWq78PgNoEYjfDGqiPS4VgIU9IXwx8vKccdx4N/c3Xz2AgpcMRNfbz2ODkFxbSq68m9bete/Ub4SAhsC4XZsO5N9QKKKps2MAwney0x8en8fvDirR8ghKia3Qsg9Sg4+0Dvfze2FaYhBY64ocOJmSzfpWxM+trg5uU309RqYeAHynHsUriwR4WE4nYEejkzqafS4fid349ypVCvciIhrFDuJdjwX+W476vg7K1uHhsiBY64LqPRyFurj2A0wl2t69Ax1OffJwV3hNYjlOM/XgK5zGFxJvZoQF0vZxIz8/li82m14whhfTb8F/IzIaAVtButdhqbIgWOuK6/jiSz40w6DnZaXh4YduMTo14He1c4vwuOrKypeKKaODvomHan8vc7d+NpEjOuqJxICCuSegL2LFaOB7wHWp2qcWyNFDjiXwqK9bzzv6MATOzegCBvlxuf7FEHuj6lHP/9uiwbt0CDWtWhU6gPBcUGPl4ry8aFqDZ/TwejHsLugtCuaqexOVLgiH9Zsj2esyXLwif1anjrB0ROATd/uBwPu+abPJ+oXhqNhv8MagbAz3vPcyQxS+VEQliB+K1w/H/KsvCo19VOY5OkwBHlZOYV8VnJsvDn+zfF1dHu1g9ydIPe/6ccb34frlw2YUJhCuHBXgxqXQejEd5dI7uNC3FbDAalqR9Ah7Hg21jdPDZKChxRzucbT5GVX0xYgDvD2gVV/IFtHwa/Zkpxs+Uj0wUUJvNi/6bY6zRsPpHKlpOpascRwnId+hkS94GDO/SU/abUIgWOKHMh4wqLtscD8NKAMHTaSnTa1Oqg31vK8c4vlD1XhEWpV8uVhzvXA+Cd/x3DYJBVcUJUWlH+1d5g3Z4BNz9V49gyKXBEmY//OkFhsYHODXzo1bQK/1E2ioL6PUFfKM3/LNRTfRrj7mTH0YtZrNh3Qe04QliemC+U3cLdA6HzE2qnsWlS4AgAjl7M4pd95wGYNrAZmqrsk6LRQL+3AQ0c+kma/1kgb1cHnuilNP/76K/j5BdJ8z8hKiwvHTaXXKLv+yo43GQFqjA5KXAEAO+vOYbRqCwZbhPsVfUnqtMa2pQ0/5NRHIs0tmsogZ5OJGbms2hbvNpxhLAcWz+BgkzwbwWth6udxuZJgSOIPn2JDcdTsdNqeKF/09t/wl7TQGsPZzYqO+gKi+Jkr+O5fsq/g7kbT5F5pUjlREJYgKxEiPlSOe77mjT1MwNS4Ng4o9HIu38oTf0eiggh1Nf19p/Uu56yNBKUURzZwsHiDG1blyb+bmTlF/PV5jNqxxHC/G3+AIrzIbgzNL5D7TQCKXBs3p+Hk9l/PhNXBx1P9a3GXg3dnwd7F7iwW2l2JSyKTqspG8VZuC2O1OwClRMJYcbSz8Der5XjqOnKfEShOilwbJjeYOTjtccBeLRbfXzdHKvvyd39IeJx5XjdW2CQyaqWpl9zf9oEeZJXqOfzjafUjiOE+drwDhiKodEdUK+L2mlECSlwbNjqA4mcSM7Bw8mO8d0bVP8LdH0KnDwh9Sgc/LH6n1+YlEaj4YX+ykacy3YkcEE24hTi35IOwcGflOO+r6qbRZQjBY6NKtIb+KRkY8XHejbE09m++l/E2Ru6PqMcb3hHNuK0QF0b1aJzAx8K9QZm/X1S7ThCmJ/1bwNGaHEP1GmjdhpxDSlwbNQve88TfykPXzcHxnQJNd0LRTwGrrUh4yzsXWK61xEmoYziKHNxftp7njOpOSonEsKMJOyEE38oG2r2fkXtNOIfpMCxQQXFematU+ZUTOrVqGIbalaVgyv0fFE53vwBFMllDkvTvp4PfcNqozcY+URGcYS4an3J9jRtR4JvI3WziH+RAscGLY85x4WMKwR4ODEyIsT0L9huNHiGQE4y7F5o+tcT1a50RdVv+xM5kpilchohzEDcFojfAjoH6PGi2mnEdUiBY2OuFOr5bIMyevNk30Y42ddAMyo7B+jxnHK8dSYU5pn+NUW1ah7owaDWdQCYtU5GcYSNMxph4wzluN0o8ApWN4+4LilwbMzX0fGkZhcQ7OPM/e1r8D/K8JHgFQK5KbB7Qc29rqg2z/RtjEYDaw4ncTgxU+04QqgnbjOc3aaM3nSbqnYacQNS4NiQvMJivizpSvt03yY42NXgX7/OHnq8oBxvnQmFuTX32qJaNPZ3567WgYCM4ggbdu3oTfsx4FlX1TjixqTAsSFLd5zlUm4hobVcGBoeWPMB2jwI3qGQlwa75tf864vb9lSfRmg0SgdsGcURNunMRkiIBp2jjN6YuRopcObMmUNoaChOTk5EREQQExNzw3MXL16MRqMpd3Nycip3jtFo5LXXXqNOnTo4OzsTFRXFyZPyG+XN5BUW88UmZfRmcu9G2OlUqG2vHcXZ9ikUyJJjS9PY353BJaM4n8qKKmFrrh296TAWPOqom0fclMk/5b7//numTp3K9OnT2bt3L23atKF///6kpKTc8DEeHh5cvHix7Hb27Nly33///feZNWsW8+bNY+fOnbi6utK/f3/y8/NN/XYs1rIdCVzKLSTEx4V72qo4pNp6BHjXh7xLsOsr9XKIKnuqrzKK89eRZA5dkFEcYUNOr4dzO8HOCbo9q3YacQsmL3A+/vhjJkyYwNixY2nevDnz5s3DxcWFhQtvvFxYo9EQEBBQdvP39y/7ntFoZObMmbzyyisMGTKE1q1b8/XXX5OYmMjKlStN/XYs0pVCPV9sPg3AlD4qjd6U0tlBz5eU422fQkG2ellElTSq7c7dbUpGcWQujrAVRqPSkR2gwzhwD1A3j7glk37SFRYWsmfPHqKioq6+oFZLVFQU0dHRN3xcTk4O9erVIzg4mCFDhnD48OGy78XFxZGUlFTuOT09PYmIiLjhcxYUFJCVlVXuZkuW7TxLWk4hwT7O6o7elGp1P/g0hCuXIeZLtdOIKniyT2O0GlgrozjCVpxeBxd2g50zdHtG7TSiAkxa4KSlpaHX68uNwAD4+/uTlJR03cc0bdqUhQsX8uuvv7J06VIMBgNdunTh/PnzAGWPq8xzzpgxA09Pz7JbcLDt9Cy4UqhnXsncmym9G2Gv5uhNKZ3d1bk40Z9LXxwL1Ki2W9kozkyZiyNsweYPla8dHgW32upmERViBp925UVGRjJq1CjCw8Pp2bMnv/zyC35+fnzxxRdVfs5p06aRmZlZdjt37lw1JjZv38YkkJZTQJC3M/e2C1I7zlWt7gOvesqKKtmjyiJN6aP0xfn7aDLHkmxrVFTYmPhtJSunHKDLk2qnERVk0gLH19cXnU5HcnJyufuTk5MJCKjY9Ut7e3vatm3LqVNK993Sx1XmOR0dHfHw8Ch3swX5RXrmbVLm3kw2l9GbUjr7q8O822ZBcYGqcUTlNartxp0tlVUkczacVjmNECa0pWT0pu3DsnLKgpj0E8/BwYH27duzbt26svsMBgPr1q0jMjKyQs+h1+s5ePAgdeoo/6jq169PQEBAuefMyspi586dFX5OW/Hj7nOkZhdQ18uZYeY0elMqfCS414HsRIj9Vu00ogqe6N0QgN8PJBKXJs0bhRW6sEdZPaXRQden1U4jKsHkv9JPnTqVr776iiVLlnD06FEmTZpEbm4uY8eOBWDUqFFMmzat7Pw333yTv/76izNnzrB3714efvhhzp49y/jx4wFlhdUzzzzD22+/zapVqzh48CCjRo0iMDCQoUOHmvrtWIwivaFs7s3jPRvUbNfiirJzhC5PKcdbPwF9sbp5RKW1CPSkT1htDEaYu/GU2nGEqH6bP1K+th6uNCoVFsPO1C8wfPhwUlNTee2110hKSiI8PJw1a9aUTRJOSEhAq7364Xv58mUmTJhAUlIS3t7etG/fnu3bt9O8efOyc1588UVyc3OZOHEiGRkZdOvWjTVr1vyrIaAtWxWbyIWMK/i6OXJ/BzOeVN1+NGz5CDLOwqGfoM0ItROJSprcuxHrj6Xwy94LPB3VhLpezmpHEqJ6JB+G478DGuguXYstjcZoNBrVDlHTsrKy8PT0JDMz0yrn4xgMRu74ZBOnU3N5eWAYj/dsqHakm9vyEax7E3ybwBM7QWuGo03iph78cgfRZy4xpksor9/dQu04QlSPnx6FQz9Di3vg/sVqpxFU7vNbPkms0F9HkjidmouHkx0jI0LUjnNrHSeAkyeknYCjq9ROI6pgSp9GAHwXk0BqtkwYF1Yg7RQc+kU57v6cullElUiBY2WMRmPZipbRXUJxd7JXOVEFOHlAp8eU4y0fKR1DhUXp0rAW4cFeFBQbWLA1Tu04Qty+rZ8ARmgyEAJaqZ1GVIEUOFZmy8k0Dl7IxNlex9iu9dWOU3GdJ4G9KyQdgJNr1U4jKkmj0TCltzKKs3THWTLzilROJMRtyEiAA8uV4x7Pq5tFVJkUOFZmzgZlJcuDnULwcXVQOU0luPhAx0eV480fyCiOBerbrDZhAe7kFBSzeHu82nGEqLptn4KhGOr3hKAOaqcRVSQFjhXZHZ/Ozrh07HUaJvSwoNGbUpFPgs4RzsdA/Ba104hK0mg0TC4ZxVm0PY7cAln2LyxQdhLs/UY5Lt1SRlgkKXCsyOcblbk3w9oFUcfTApfquvtDu1HK8eYP1M0iquTOVnVo4OtKRl4Ry3aeVTuOEJW3fTboCyA4AkK7qZ1G3AYpcKzE4cRM1h9LQauBx8x9WfjNdH0atHYQtxnO7VI7jagknVbD472Uf39fbYkjv0ivciIhKiEvHXYvUo57vAAajbp5xG2RAsdKzC0ZvRnUOpD6vq4qp7kNXsHQuqTZ3/ZP1c0iquSetnWp6+VManYBP+62nY1thRXYtQCKcpVVU42i1E4jbpMUOFbgTGoOvx+8CMATvSx49KZU6W69R1crvSiERbHXaZnYowGgjOLoDTJhXFiAoiuwc55y3PUZGb2xAlLgWIEvNp3BaIS+YbVpVscKOjPXDlN6T2CE7bPUTiOq4IEOwXi72JOQnseaQ0lqxxHi1mKXQV4aeIZA86FqpxHVQAocC5eclc8v+84DV3d2tgqlu/bu/w6yk9XNIirN2UHHqMhQAOZtOo0N7ggjLIlBr0wuBugyBXQm36ZR1AApcCzcwm1xFOmNdAz1pn09H7XjVJ+QzhDUCfSFV4eNhUUZFVkPJ3stBy9kEn3mktpxhLixo6vgcjw4e0Pbh9VOI6qJFDgWLDu/iG93JAAwsYcVjd6Acv27dBRn1wIoyFY3j6i0Wm6OPFCyk/0Xm86onEaIGzAaYetM5bjTRHCw4EUaohwpcCzY8phzZBcU09DPlb5htdWOU/2a3gm1GkNBJuxZonYaUQXjuzVAq4FNJ1I5ejFL7ThC/Fv8FrgYC3bOSoEjrIYUOBaqSG9g4TZlU8MJ3Rug1VrhjH+tFro+pRzv+ByKC9XNIyotpJYLA1vVAeCrzTKKI8zQtpJ2FG0fBldfdbOIaiUFjoX6bX8iFzPz8XN3ZGjbumrHMZ3Ww8HNH7IuwKGf1U4jquCxkiXjq/YnciHjispphLhG0iE49TdotBA5We00oppJgWOBjEYjX5b8NjymSyhO9jqVE5mQnaOy0zgov2nJahyL0zrIiy4Na1FsMLJwa5zacYS4qrQNRfOh4GOB+/eJm5ICxwJtPpnGsaRsXBx0PBxRT+04ptd+LDi4Q+pROLlW7TSiCkob/y2PSSAzr0jlNEIAGQlw8CfluPRSuLAqUuBYoC83K9syjOgYgqeLvcppaoCzF3QYoxxvk+0bLFHPJn6EBbiTW6hnqWzCKczBjrlg1EP9nhDYVu00wgSkwLEwhy5ksu3UJXRaDY92C1U7Ts2JmARaezi7Fc7vVjuNqCSNRsNjPZVRnEXb4mUTTqGuvPSrKzNL21EIqyMFjoUpnXtzV+s6BHm7qJymBnnWhdYPKMfbZqoaRVTNXa0DCfR0Ii2ngBX7LqgdR9iy0k01/VtBwz5qpxEmIgWOBTl/Oa9sU83SOQ02pUvJdfKjq+HSaXWziEqz12l5tJsykfOrzWcwyCacQg1F+RDzhXLc9SnZVNOKSYFjQRZsVXZm7tbIlxaBnmrHqXm1w6BxP8CoXD8XFmdEpxA8nOw4k5bL2qOyx5hQwcEfITcVPIKgxT1qpxEmJAWOhcjMK+L7XecAGx29KVXaqyJ2mXIdXVgUN0c7RnZWVv4t2CJLxkUNMxoheo5yHPEY6GxgkYYNkwLHQizdeZa8Qj3N6njQvbENd9us31O5bl6UB3sWq51GVMGYLqHY6zTExKez/1yG2nGELTmzQWk3Ye8K7UapnUaYmBQ4FqCw2MCS7fEATOxRH40tXzPWaK6O4sR8Kds3WCB/DycGtw4ElMuuQtSY0tGbdo8o7SeEVZMCxwKsPpBISnYB/h6ODGoVqHYc9bUcBm4BkH0RDq9QO42ogtLJxr8fvEiibN8gakLKUWVbBjQQ8bjaaUQNkALHzBmNxrLfckdFhuJgJ39l2DlApwnKcfRs2b7BArWs60nnBj7oDcay0UkhTGrH58rXZnfJtgw2Qj4tzdzOuHQOJ2bhZK9lZESI2nHMR4dHwd4Fkg5C/Ba104gqGN9NmSz/bUwCOQXFKqcRVi0nFfZ/rxx3lk01bYUUOGZufslKk2HtgvBycVA5jRlx8YHwh5Tj0uvqwqL0CatNfV9XsvOL+XH3ObXjCGu2eyHoCyCwHYR0VjuNqCFS4Jix+LRc1h1TeoWUzlkQ14iYBGjgxBpIO6l2GlFJWq2m7N/1wm1Kjychql1RPuz6SjmOnCyN/WxIjRQ4c+bMITQ0FCcnJyIiIoiJibnhuV999RXdu3fH29sbb29voqKi/nX+mDFj0Gg05W4DBgww9duocYu2xWE0Qu+mfjT0c1M7jvnxbQRNByrHMopjkYa1q4uXiz3n0q+w9kiS2nGENbq2sV/zIWqnETXI5AXO999/z9SpU5k+fTp79+6lTZs29O/fn5SUlOuev3HjRh588EE2bNhAdHQ0wcHB9OvXjwsXyu9dM2DAAC5evFh2++6770z9VmpU5pUiftxzHoBx3Wy4sd+tRE5Rvu7/DnIvqZtFVJqLg13Z3LL50vhPVLdyjf0mSmM/G2PyAufjjz9mwoQJjB07lubNmzNv3jxcXFxYuHDhdc9ftmwZTzzxBOHh4YSFhTF//nwMBgPr1q0rd56joyMBAQFlN29vb1O/lRq1PCaBvEI9YQHudG1US+045qteF6gTDsX5ynV2YXFGRSqN/3afvcy+hMtqxxHWpFxjv9FqpxE1zKQFTmFhIXv27CEqKurqC2q1REVFER0dXaHnyMvLo6ioCB8fn3L3b9y4kdq1a9O0aVMmTZrEpUs3/u29oKCArKyscjdzVqy/2tjv0a423tjvVjSaq6M4MV9CcYG6eUSl+Xs4MbiNNP4TJiCN/WyaSQuctLQ09Ho9/v7+5e739/cnKali19tfeuklAgMDyxVJAwYM4Ouvv2bdunW89957bNq0iYEDB6LX66/7HDNmzMDT07PsFhwcXPU3VQP+OJREYmY+vm4O3B0ujf1uqcVQ8KgLuSlw8Ce104gqGFcy2fiPQ0mcv5ynchphFaSxn80z61VU7777LsuXL2fFihU4OTmV3T9ixAjuvvtuWrVqxdChQ1m9ejW7du1i48aN132eadOmkZmZWXY7d868l6SW/hY7MqIeTvY6ldNYAJ29snEeKL+xSeM/i9Mi0JMuDWtJ4z9RfUob+4UNksZ+NsqkBY6vry86nY7k5ORy9ycnJxMQEHDTx3744Ye8++67/PXXX7Ru3fqm5zZo0ABfX19OnTp13e87Ojri4eFR7mau9py9TOy5DBx0Wh4u2XVZVEC70cp19pTDELdZ7TSiCsZ3Vz6ElsecIzu/SOU0wqLlpl1t7Fd6CVvYHJMWOA4ODrRv377cBOHSCcORkZE3fNz777/PW2+9xZo1a+jQocMtX+f8+fNcunSJOnXqVEtuNS0sGb0ZEh6In7ujymksiLMXhD+oHO+cp2oUUTW9mtSmgZ8r2QXF/FSyglCIKtm1QBr7CdNfopo6dSpfffUVS5Ys4ejRo0yaNInc3FzGjh0LwKhRo5g2bVrZ+e+99x6vvvoqCxcuJDQ0lKSkJJKSksjJyQEgJyeHF154gR07dhAfH8+6desYMmQIjRo1on///qZ+OyZ1/nIefxy6CMC47jKkWmml19mP/wHpZ9TNIipNq9UwpksoAEu2x2OQxn+iKqSxnyhh8gJn+PDhfPjhh7z22muEh4cTGxvLmjVryiYeJyQkcPHixbLz586dS2FhIffddx916tQpu3344YcA6HQ6Dhw4wN13302TJk0YN24c7du3Z8uWLTg6WvaIx5Lt8RiM0LVRLcICzPcymtnybQyNogAj7PxS7TSiCoa1C8LdyY74S3lsOH79XllC3FRZY7+60tjPxmmMRtubkZmVlYWnpyeZmZlmMx8np6CYyHfWkV1QzMIxHegT5n/rB4l/O/U3LB0GDu4w9Qg4mcffr6i4//5+hK+2xNGtkS9Lx0eoHUdYEqMR5naBlCNwx5vQ9Wm1E4lqVpnPb7NeRWVLftx9juyCYhr4udKrSW2141iuhn3BtwkUZkPst2qnEVUwKjIUrQa2nkrjRHK22nGEJYnbrBQ30thPIAWOWdAbjCzaFg/A2K710WrlmnGVaTRXl4zvnAcGg7p5RKUF+7hwR3NlBLP0vwshKmTnF8rX8AelsZ+QAscc/H00mYT0PDyd7RnWrq7acSxfmwfByRMux8HJP9VOI6pgbFdlkv2KfefJyCtUOY2wCJfj4fj/lONOE1WNIsyDFDhmoLSx30MRIbg42Kmcxgo4XDM8vWOuullElUTU96FZHQ/yiwx8F2PejTmFmYj5CjBCwz7g11TtNMIMSIGjssOJmcTEpaPTahgVKY39qk2nCaDRQtwmSD6idhpRSRqNhrFdQwH4JjqeYr1cahQ3UZADe79RjmVbBlFCChyVlbalH9gygDqezuqGsSZeIRB2l3Isjf8s0t1tAqnl6kBiZj5/Hk6+9QOE7TrwPRRkgnd9aHSH2mmEmZACR0XpuYWsjE0EKPttVVSjzk8oXw98D3np6mYRleZkr2NkRAgAi7bJLuPiBozGq5OLIx4DrXysCYX8S1DRdzEJFBYbaFXXk3Yh3mrHsT4hnaFOGyjOhz2L1E4jquDhzvWw12nYffYyB89nqh1HmKMzGyHtODi4QfhDaqcRZkQKHJUU6Q0s3XEWgDFdQtFIO/Hqp9FAxCTlOGY+6GUDR0tT28OJQa2UPeZkFEdcV9nS8IeU1ZNClJACRyV/HU7mYmY+vm4O3NXG8jcJNVst7wXX2pCdCEdXqZ1GVEHpkvHfDiSSkp2vchphVtLPwIk1yrEsDRf/IAWOShZvL1ka3ikERzudymmsmJ0jdBynHO+QycaWqE2wF+1CvCjSG1m2I0HtOMKcxMwHjMoedL6N1U4jzIwUOCo4dCGTXfGXsdNqGNlZloabXIdHQecA52Pg/B6104gqKB3FWbbzLAXFepXTCLNQkAP7ZGm4uDEpcFSwuGRp+J2t6uDv4aRuGFvgVhtaDlOOd0rjP0s0oGUAAR5OpOUUsnr/RbXjCHOw/zsoyAKfhsoedEL8gxQ4NSwtp4BVJUvDx8jS8JpT+hve4RWQJR+QlsZep+WRkkaYC7fFYTQaVU4kVGUwQMyXyrEsDRc3IP8qatjymAQK9QbaBHnSNthL7Ti2IzAcQrqAoRh2L1A7jagCZb6alsOJWeyKv6x2HKGmMxsg7QQ4uCt7zwlxHVLg1KAivYFvSpeGd5Wl4TWuc8kozu6FUCSrcSyNt6sD95ZsRitLxm1c6dLwtg+Dk4e6WYTZkgKnBq05lERyVgG+bo7c2UqWhte4poPAMwTyLsGhn9ROI6pgTBdlsvGfh5M4fzlP5TRCFZdOw8k/AY2y55wQNyAFTg0qnVw8MkKWhqtCZwedxivHO+cpLd6FRWka4E7XRrUwGGGpLBm3TTFfKV8b94NaDdXNIsyaFDg15MD5DPacvYy9TlO2v45QQdtHwM4Zkg5CQrTaaUQVlI7ifBeTwJVCWTJuUwqyYd9S5TjiMXWzCLMnBU4NKR29GdSqDrVlabh6XHygzXDlWHYZt0h9wmoT7ONM5pUiVsZeUDuOqEmx30JhNvg2gYZ91E4jzJwUODUgNbugrHfHmJKGZUJFnUp+8zu6GjLOqZtFVJpOq2F0ZCgAi7fFy5JxW2EwXJ1c3GmistecEDchBU4N+K5kaXh4sBfhsjRcff7NoX5PMOph13y104gquL9DMC4OOo4nZxN95pLacURNOL0O0k+Do4csDRcVIgWOiRUWX901fKw09jMfpY3/9i6BQlmNY2k8ne0Z1i4IUEZxhA0ovaTc9hFwdFM3i7AIUuCY2B+HLpKSXYCfuyMDW8rScLPRpD941YMrl+HgD2qnEVUwuovS2fjvo8mcS5ci1aqlnYRTf6MsDR+vdhphIaTAMbHSycUPR9TDwU5+3GZDq7u6CmPnF7Jk3AI1qu1O98a+GIyUNdAUVqp0W4YmA8CngbpZhMWQT1wTij2Xwb6EDOx1Gh6SpeHmJ3wk2LtCyhGI36J2GlEFpZd9l8ckkFdYrG4YYRr5mcrqKZCl4aJSpMAxoSUlozeDWwfi5+6obhjxb85eEF4yWbF0dYawKL2a1KZeLRey8ov5Za8sGbdKsd9CYQ74NoUGvdROIyyIFDgmkpKdz+oDyq7ho7uEqhtG3FjpkvFjv8PleFWjiMrTXrtkfLssGbc61y4Nj3hMloaLSpECx0S+3ZlAkd5IuxAv2sjScPPl1wQa9gWMV1vAC4tyX4cgXB10nErJYdspWTJuVU6thctx4OgJbUaonUZYGClwTEBZGq7skyON/SxA2ZLxb6AgR90sotI8nOy5v0MwAIu3yy7jVqV0aXi7R8DBVd0swuJIgWMC/zt4kbScAvw9HBnYMkDtOOJWGkWBT0MoyIQDy9VOI6pgVKSyZHzdsRTOXspVOY2oFqnH4fR60GiVzsVCVFKNFDhz5swhNDQUJycnIiIiiImJuen5P/74I2FhYTg5OdGqVSv+97//lfu+0Wjktddeo06dOjg7OxMVFcXJkydN+RYqZdE1S8PtdVJDmj2tVpaMW7gGfm70auqH0QhfR8uScatQujS86Z3gXU/dLMIimfzT9/vvv2fq1KlMnz6dvXv30qZNG/r3709KSsp1z9++fTsPPvgg48aNY9++fQwdOpShQ4dy6NChsnPef/99Zs2axbx589i5cyeurq7079+f/Px8U7+dW9qXcJn95zJw0Gl5UJaGW442D4KDO6SdgDMb1E4jqmBMyWT+H3adI7dAloxbtCsZEPudcixLw0UVmbzA+fjjj5kwYQJjx46lefPmzJs3DxcXFxYuXHjd8z/99FMGDBjACy+8QLNmzXjrrbdo164dn332GaCM3sycOZNXXnmFIUOG0Lp1a77++msSExNZuXKlqd/OLZU29hvcJhBfN1kabjGcPKDtSOVYloxbpB6N/Wjg60p2QTE/7z2vdhxxO2KXQVEu1G4Ood3VTiMslEkLnMLCQvbs2UNUVNTVF9RqiYqKIjo6+rqPiY6OLnc+QP/+/cvOj4uLIykpqdw5np6eRERE3PA5CwoKyMrKKnczhZSsfH4/ULJruCwNtzydJgIaOPEnXDqtdhpRSVqtpqwlw+Lt8RgMcqnRIhn0Vy9PydJwi3QiOZvHv9nDTpU3wjVpgZOWloZer8ff37/c/f7+/iQlJV33MUlJSTc9v/RrZZ5zxowZeHp6lt2Cg4Or9H5uZdnOBIoNRjrU86ZVkKdJXkOYUK2G0LgfsmTccg1rH4Sbox1nUnPZcipN7TiiKk7+pfSkcvKCVg+onUZUweLt8aw5nMQilTfCtYkZsNOmTSMzM7Psdu7cOZO8zrB2QYzvVp+JPWSvFItVer1/31IoyFY3i6g0N0c77u9Qusu4LBm3SKVLw9uPBgcXdbOISsvMK2JFSVfxMSVbqajFpAWOr68vOp2O5OTkcvcnJycTEHD95dMBAQE3Pb/0a2We09HREQ8Pj3I3Uwip5cIrdzWnXwtZGm6xGvYB3yZQmH11/xthUUZHhqLRwIbjqcSlyZJxi5JyDM5sVJaGd5Rdwy3RD7vPcaVIT1iAOxH1fVTNYtICx8HBgfbt27Nu3bqy+wwGA+vWrSMyMvK6j4mMjCx3PsDatWvLzq9fvz4BAQHlzsnKymLnzp03fE4hKkyjudpzY+cXSqt4YVFCfV3p07Q2cHU/OGEhYkom+IcNAi9ZhWpp9AYjS6LjAWUeqkbl+VMmv0Q1depUvvrqK5YsWcLRo0eZNGkSubm5jB07FoBRo0Yxbdq0svOffvpp1qxZw0cffcSxY8d4/fXX2b17N1OmTAFAo9HwzDPP8Pbbb7Nq1SoOHjzIqFGjCAwMZOjQoaZ+O8IWtHlQaQ2ffhpOr7v1+cLslA6N/7TnPNn5ReqGERVz5TLsL2m0WdpdXFiU9cdSOH/5Cl4u9gwJr6t2HOxM/QLDhw8nNTWV1157jaSkJMLDw1mzZk3ZJOGEhAS02qt1VpcuXfj222955ZVX+M9//kPjxo1ZuXIlLVu2LDvnxRdfJDc3l4kTJ5KRkUG3bt1Ys2YNTk5Opn47whY4uimt4aM/gx1zofEdaicSldStkS+NartxKiWHn/acZ6xsmWL+9n4DRXng3xLqdVU7jaiC0q1SRnQMwdlBp3Ia0BhtcPvdrKwsPD09yczMNNl8HGHh0uNgVlvACJN3KZtyCovyzY6zvLryEKG1XFj/XC+0WllubLYMepgVDhkJcPdsaDdK7USikk4kZ9Pvk81oNbD5xd4EeZtmgnhlPr9tYhWVEJXmU19pEQ9Xe3IIi3Jv27q4O9kRfymPTSdS1Y4jbub4H0px4+wNre5XO42ogtL5bv2aB5isuKksKXCEuJHSJeOx30J+prpZRKW5OtoxvGSX8UUy2di8lS0NHwP2zqpGEZWXmVfELyVLw0ebUZNbKXCEuJH6PcCvmdIyft9StdOIKhhVsmR884lUTqXkqB1HXE/yYYjfAhqdLA23UNcuDe/cQN2l4deSAkeIG9Foro7ixHypzBMQFiWklgt9w5QFDV+XLF8VZqZ09KbZYPAMUjeLqDS9wcjXO+IB81gafi0pcIS4mdbDlZbxl+OVFvLC4jx6zZLxLFkybl7y0uHAD8qxLA23SOuPpXAu/QqezuaxNPxaUuAIcTMOLkrLeFCWjAuLE9mwFk383cgr1PPjbtll3KzsXQLF+RDQGkI6q51GVEHp5OIRnYLNYmn4taTAEeJWOo5XWsfHbYKUo2qnEZWk0WgY00Xpg7Nkezx62WXcPOiLIWa+ctx5kuwaboFOJmez9VQaWg080rme2nH+RQocIW7FKwTC7lKOd36hbhZRJUPbBuLpbE9Ceh4bjqWoHUcAHFsNWefBxRda3Kt2GlEFi0tGb+5o7m82S8OvJQWOEBVROj9g/3KlpbywKC4OdozoqCwZXyxLxs1D6S8LHcaCvXShtzSZV64uDS8dITU3UuAIURH1uoB/Kyi+Anu/VjuNqIKHO9dDq4Gtp9I4mZytdhzbdnE/JGwHrR10GKd2GlEFP5YsDW/qb15Lw68lBY4QFVFuyfhXyvwBYVGCfVy4o7myZFxGcVRWOnrTfCh41FE1iqi8cruGdzWvpeHXkgJHiIpqdT+41ILMc3DiD7XTiCooHUr/Ze8FMvNkybgqclLh4I/KsSwNt0gbrlkaPtTMloZfSwocISrK3klpJQ+wY56qUUTVdG7gQ1iAO1eK9Pyw+5zacWzT3sWgL4TAdhDUQe00ogpKR0BHdDS/peHXkgJHiMroME5pKX92KyQdVDuNqCSNRsPYksZ/S6JlyXiN0xfBrgXKccTjsjTcAl27NPxhM1wafi0pcISoDM+60HyIcixLxi3SkPC6eLnYc/7yFf4+mqx2HNty5FfIvghu/tDiHrXTiCq4dml4sI/5LQ2/lhQ4QlRW6byBgz9C7iV1s4hKc7LX8WCnEAAWb4tXN4ytKVsa/ijYOaibRVRaRl6hWe4afiNS4AhRWcGdoE640mJ+72K104gqeLhzPXRaDdFnLnEsKUvtOLbhwh44HwNae2g/Vu00ogqW77q6a3hkg1pqx7klKXCEqCyN5uoozq4FyrwCYVHqejnTv4WyZHyJLBmvGTu/VL62vBfc/dXNIiqtWG/g65L/Vh7tVt9sl4ZfSwocIaqi5b3g6gdZF5SW88LilC4ZX7HvApdzC1VOY+Wyk+HQz8pxaT8pYVH+OpJMYmY+tVwduLtNoNpxKkQKHCGqws5RmUcAsmTcQnUM9aZ5HQ/yiwx8L0vGTWvPIjAUQVAnqNte7TSiChZujQPgoYgQnOzNd2n4taTAEaKqOjyqtJo/twMS96mdRlTStUvGv94eT7HeoG4ga1VceM3ScBm9sUQHzmew++xl7HUas18afi0pcISoKveAq0tdS+cXCIsyuE0gPq4OJGbms/aILBk3iSMrITcF3OtcbbEgLMqiktWGg1rVwd/DcjZGlQJHiNsRMUn5eugnyElRN4uoNCd7HQ+VLBlfJJONq5/RCDvmKscdxoHOXt08otJSsvJZfSARUCYXWxIpcIS4HUHtoW4HpfX8nsVqpxFVULpkPCYuncOJmWrHsS7nd0PiXtA5QgdZGm6Jlu5MoEhvpH09b1oHeakdp1KkwBHidl27ZLxYVuNYmgBPJwa2DABkyXi121kyAb/VfeDqq24WUWn5RXqW7TgLwKNdLWv0BqTAEeL2NR8CbgGQkwRHV6mdRlRB6WTjlbGJpMuS8eqRdVGZfwPQaaKqUUTV/LY/kUu5hQR6OpX1jbIkUuAIcbvsHKDjOOW4dL6BsCjtQrxpVdeTwmID38UkqB3HOuyaD4ZiCImEwHC104hKMhqNLCyZXPxIZCh2OssrFywvsRDmqP0Y0DnAhd3KvANhUTQaDWNK9tZZuuMsRbJk/PYU5sHukqXhnSepm0VUyc64dI5ezMLJXsuDnYLVjlMlUuAIUR3cakPLYcqx7DJuke5qUwdfNwcuZubz5+EkteNYtgPL4cpl8KoHYXepnUZUwaJtSmO/e9sF4eVimRujSoEjRHUpbWJ2eAVkywekpXG00/FQhNLETHYZvw0Gw9VLtRGPg9Yyut6Kq86l5/FXSV+osRawa/iNSIEjRHUJbAvBnZWW9LsXqp1GVMHDESHYaTXsPnuZg+dlyXiVnF4HaSfAwR3aPqx2GlEFS7bHYzRC98a+NPZ3VztOlZm0wElPT2fkyJF4eHjg5eXFuHHjyMnJuen5Tz75JE2bNsXZ2ZmQkBCeeuopMjPL/49Go9H867Z8+XJTvhUhKqZ0FGf3QiguUDeLqLTaHk4Mal0HgMWyZLxqoj9TvrYbBU4e6mYRlZZTUMz3u5S92Sxxafi1TFrgjBw5ksOHD7N27VpWr17N5s2bmTjxxssFExMTSUxM5MMPP+TQoUMsXryYNWvWMG7cuH+du2jRIi5evFh2Gzp0qAnfiRAV1GwweNSF3FTlUpWwOKWTjX/bn0hqthSplZJ8GM5sBI1W9p2yUD/vOU92QTENfF3p2cRP7Ti3xWQFztGjR1mzZg3z588nIiKCbt26MXv2bJYvX05iYuJ1H9OyZUt+/vlnBg8eTMOGDenTpw///e9/+e233yguLi53rpeXFwEBAWU3JyfL2R9DWDGdffkl40ajunlEpbUN8SY82ItCvYGlJU3ORAXt+Fz52mwweFvOpoxCYTAYy0Yux3QNRavVqBvoNpmswImOjsbLy4sOHTqU3RcVFYVWq2Xnzp0Vfp7MzEw8PDyws7Mrd//kyZPx9fWlU6dOLFy4EONNPkgKCgrIysoqdxPCZNqNUVrTX4yFczFqpxFVML67MjS/dMdZ8ov0KqexEDkpcOBH5bjzZHWziCrZeCKFuLRc3J3sGNYuSO04t81kBU5SUhK1a9cud5+dnR0+Pj4kJVVshUlaWhpvvfXWvy5rvfnmm/zwww+sXbuWYcOG8cQTTzB79uwbPs+MGTPw9PQsuwUHW+aafmEhXGtB6/uV49JW9cKiDGgRQF0vZy7lFrJy3wW141iGXQtAXwB120NwJ7XTiCpYsFVZGj6iYzCujna3ONv8VbrAefnll687yffa27Fjx247WFZWFoMGDaJ58+a8/vrr5b736quv0rVrV9q2bctLL73Eiy++yAcffHDD55o2bRqZmZllt3Pnzt12PiFuqnR/qiO/QuZ5dbOISrPTacu2b5i/Ne6mI8QCKMpXOhcDdH4CNJZ9acMWHUnMYtupS+i0GkZb8NLwa1W6wHnuuec4evToTW8NGjQgICCAlJSUco8tLi4mPT2dgICAm75GdnY2AwYMwN3dnRUrVmBvb3/T8yMiIjh//jwFBdefEOjo6IiHh0e5mxAmFdAKQruDUS+N/yzUAx2DcXO041RKDptOpKodx7wd/BHy0pQJ9s2HqJ1GVMH8rWcAGNgygCBvF5XTVI9Kj0H5+fnh53frmdWRkZFkZGSwZ88e2rdvD8D69esxGAxERETc8HFZWVn0798fR0dHVq1aVaHJw7GxsXh7e+Po6FjxNyKEqUVOgfgtsGcJ9HwRHC23n4Qt8nCyZ3jHYBZsjWPB1jh6Na196wfZIqPxmsZ+jykT7YVFSc7K57f9yuKf8d0bqJym+phsDk6zZs0YMGAAEyZMICYmhm3btjFlyhRGjBhBYGAgABcuXCAsLIyYGGUiZlZWFv369SM3N5cFCxaQlZVFUlISSUlJ6PXKRL/ffvuN+fPnc+jQIU6dOsXcuXN55513ePLJJ031VoSomsb9oFZjKMiEvd+onUZUwZguoWg1sOVkGseSZHHCdZ3ZCCmHwd4V2o1WO42ogiXb4ynSG+kYqqwgtBYm7YOzbNkywsLC6Nu3L3feeSfdunXjyy+/LPt+UVERx48fJy8vD4C9e/eyc+dODh48SKNGjahTp07ZrXTejL29PXPmzCEyMpLw8HC++OILPv74Y6ZPn27KtyJE5Wm1EFmymmTHXNAX3/x8YXaCfVwY2FJp/LdgS5zKacxU9Bzla9uR4OylahRReXmFxSzbmQBY1+gNgMZog7PnsrKy8PT0LFuCLoTJFF2BT1pA3iW4bxG0vFftRKKS9iZc5t7Pt+Og07L15d7UdpeeW2VSj8OcToAGntwDtRqqnUhU0tfR8bz262Hq1XJh/XO90Jl575vKfH7LXlRCmJK9M3QcrxxHfyaN/yxQuxBv2oWUNP6LlsZ/5ZTOvWl6pxQ3FkhvMLKwZGn4uG71zb64qSwpcIQwtY4TlMZ/F/bAuYo3uRTmo3To/htp/HdV7iXYX7IHYOQT6mYRVfL30WTiL+Xh6WzPfe0tv7HfP0mBI4SpuflBm+HK8fYbN6QU5qtfc3+CvJ25nFfEL3ul8R8AexZC8RUIaA31uqqdRlRB6byykREhuDhYfmO/f5ICR4iaEDlF+Xrsd7h0Wt0sotKUxn/K9g0Ltp7BYLDxS43FhRBT0tgvcrI09rNA+89lEBOfjr3Oehr7/ZMUOELUBL+myrJxrukZIizKAx2CcHe043RqrjT+O/wL5CSBWwC0kInzluirLUpjv8FtAvH3sM6J81LgCFFTSpeMxy6DvHR1s4hKc3eyZ0QnZR+70g8Hm2Q0wrZZynGnCWDnoG4eUWnnL+fxxyFlT8jx3axrafi1pMARoqbU7wn+raAoD/YsUjuNqILRXULRaTVsP32JQxcy1Y6jjlPrrjb26zhO7TSiChZvi0dvMNK1US2aB1pvqxQpcISoKRoNdCmZi7PzS2Ueg7AoQd4u3NVaafz35WYbHcXZ/qnytf1ocPZWN4uotOz8IpbvUhrnWltjv3+SAkeImtTiXnCvo8xfOPST2mlEFUzsoXwo/H7wIufS81ROU8MS90HcZtDolF3DhcVZHnOOnIJiGtV2o2fjW+8racmkwBGiJtk5KBsSAmyXxn+WqEWgJ90b+6I3GFmw1ca2byide9NyGHgFq5tFVFphsaHs3+yE7vXRWlljv3+SAkeImtZ+DDi4KfMYTv2tdhpRBY/1ULr2fr/rHJdzbeRS4+V4OLJSOe76lJpJRBX9GnuBpKx8ars7MrRtXbXjmJwUOELUNGdvpcgB2PapqlFE1XRtVIsWgR5cKdLzzQ4b2b4heg4YDdCwDwS0UjuNqCSDwVg2b+zRbvVxtNOpnMj0pMARQg2dnwCtPcRvgfN71E4jKkmj0ZTNxVm8Pd76t2/IS4d9S5XjLjJ6Y4nWH0vhZEoO7o52PBQRonacGiEFjhBq8KwLrR9Qjrd9om4WUSWDWtWhrpcz6bmF/LjnvNpxTGvXfKW9QUBraNBL7TSiCr7YrHRQf6hzCB5O9iqnqRlS4Aihlq5PK1+Proa0k+pmEZVmp9MyobuyfcP8LWfQW+v2DUVXYOcXynHXp2VbBgu052w6u+Iv46DT8mjJliO2QAocIdTi1xSa3gkYYfsstdOIKnigYzBeLvacvZTHn4eT1I5jGrHfQl4aeIZA86FqpxFVMG+TMvfmnrZ1rXZbhuuRAkcINZWO4uxfDtlW+gFpxVwc7BjVuR4AX2w6jdHalv0b9BD9mXIcORl01rfjtLU7lZLN2iPJaDQwsad1N/b7JylwhFBTSGcI7gz6QtjxudppRBWM6hKKo52W/ecz2XHGyvYYO7Ya0s+Akxe0fVjtNKIKSldO3dHMn4Z+biqnqVlS4Aihtm7PKF93L4J8G93fyIL5ujlyf4cgAL4smchpFYzGq20MOo4HR9v6cLQGSZn5rNh3AYDHezVUOU3NkwJHCLU17g9+YVCQpRQ5wuKM79YAjQY2HE/lWFKW2nGqx9ltcGEP6Byvdt8WFmXRtjiK9EY6hfrQLsT29g2TAkcItWm1V+fi7JgLxQXq5hGVFurrysCWAQB8uclKNuHc8pHyNfwhcKutbhZRaZlXili2MwGAx3vZ1tybUlLgCGEOWt4HHnWVTTj3L1c7jaiC0u0bft2faPmbcF7YA6fXK5tqll5CFRZl2c6z5BQU09Tfnd5NbbNAlQJHCHNg56CsUgFlybjByjvjWqE2wV5lm3DO22Thc3G2fKx8bXU/eIeqGkVUXn6RnkXb4gGY2KMBGhvtXSQFjhDmot1oZbXKpVNw7He104gqmNy7EQA/7j5Pcla+ymmqKOWYsnoKoNuz6mYRVfLTnvOkZhdQx9OJu8MD1Y6jGilwhDAXjm7QaYJyvPVjZRWLsCgR9X3oUM+bQr2BrzZb6FycrSWjN80GQ+0wdbOISivSG5i7URlBfKxHA+x1tvsxb7vvXAhzFPE42LtA4j44vU7tNKKSNBoNk/soozjLdiZwObdQ5USVlB4HB39Sjrs/p24WUSW/xiZyIeMKvm4OjOhkG5tq3ogUOEKYE1df6PCocrzpAxnFsUC9mvjRsq4HV4r0LNoWp3acytn2KRj10LAvBLZVO42oJL3ByOcbTgEwoXsDnOx1KidSlxQ4QpibLk8qvUfO7YD4rWqnEZWk0WiY3EsZxVm8PZ7s/CKVE1VQ1kWIXaYcy+iNRfrfwYucScvFy8WekSVbiNgyKXCEMDfuAdBulHK8+X11s4gq6d8igEa13cjKL+abHWfVjlMx0Z8pW4aEREJoV7XTiEoyGIx8tl4ZvXm0a33cHGXfMClwhDBHXZ8GrT3EbYaEnWqnEZWk1Wp4oqQ1/oItcVwpNPNl/3npsHuhciyjNxbp76PJHE/Oxt3RjtFdQtWOYxakwBHCHHkFQ/iDyvHmD9TNIqrk7jaBBPs4cym3kOW7EtSOc3M75kJRHgS0hkZRaqcRlWQ0GvmsZO7NqC718HS2VzmReTBpgZOens7IkSPx8PDAy8uLcePGkZOTc9PH9OrVC41GU+72+OOPlzsnISGBQYMG4eLiQu3atXnhhRcoLi425VsRouZ1e1bpJHtqLVzYq3YaUUl2Oi2P91RGcb7cfIbCYoPKiW4gPwtivlCOuz8HNtoUzpJtPpnGgfOZONvreLRrfbXjmA2TFjgjR47k8OHDrF27ltWrV7N582YmTpx4y8dNmDCBixcvlt3ef//qPAS9Xs+gQYMoLCxk+/btLFmyhMWLF/Paa6+Z8q0IUfN8GiidZOHqvkDCotzXPgh/D0cuZubzy97zase5vt0LlF3sazVWet8Ii2I0Gpm97iQAD0WEUMvNUeVE5sNkBc7Ro0dZs2YN8+fPJyIigm7dujF79myWL19OYmLiTR/r4uJCQEBA2c3Dw6Pse3/99RdHjhxh6dKlhIeHM3DgQN566y3mzJlDYaGF9ZwQ4la6PwdolM6ySYfUTiMqydFOx4TuykaHczedplhvZqM4hXkQPUc57j4VtLa9rNgS7YxLZ/fZyzjotEzsYZubat6IyQqc6OhovLy86NChQ9l9UVFRaLVadu68+aTJZcuW4evrS8uWLZk2bRp5eVc3rouOjqZVq1b4+/uX3de/f3+ysrI4fPjwdZ+voKCArKyscjchLIJfE2gxVDmWURyL9FBECD6uDpy9lMfvBy+qHae8PYsgNxU8Q66OFgqLUrpy6oGOQfh7OKmcxryYrMBJSkqidu3yO5ja2dnh4+NDUlLSDR/30EMPsXTpUjZs2MC0adP45ptvePjhh8s977XFDVD25xs974wZM/D09Cy7BQcHV/VtCVHzuj+vfD28AlJPqJtFVJqLgx3juinzImatO4neYCbNGwvzYOtM5bjH86CTiamWZm/CZbaeSsNOqynbzV5cVekC5+WXX/7XJOB/3o4dO1blQBMnTqR///60atWKkSNH8vXXX7NixQpOn6767rzTpk0jMzOz7Hbu3LkqP5cQNS6gJTQdBBiv7hMkLMqoyHp4udhzOjWX1Qdufom+xuxZBLkp4BUCbR5UO42ogjklozf3tK1LsI+LymnMT6ULnOeee46jR4/e9NagQQMCAgJISUkp99ji4mLS09MJCAio8OtFREQAcOqU8hcZEBBAcnJyuXNK/3yj53V0dMTDw6PcTQiL0qOkN8mBH5T9goRFcXeyL5uL86k5jOIUXVG2ZQBlhNDOQd08otIOns9k3bEUtBqY1EtGb66n0gWOn58fYWFhN705ODgQGRlJRkYGe/bsKXvs+vXrMRgMZUVLRcTGxgJQp04dACIjIzl48GC54mnt2rV4eHjQvHnzyr4dISxD3fbK/kBGPWz5UO00ogpKR3HOpOby236VR3F2L4KcZBm9sWCf/K1crh4SXpcGfm4qpzFPJpuD06xZMwYMGMCECROIiYlh27ZtTJkyhREjRhAYGAjAhQsXCAsLIyYmBoDTp0/z1ltvsWfPHuLj41m1ahWjRo2iR48etG7dGoB+/frRvHlzHnnkEfbv38+ff/7JK6+8wuTJk3F0lOVxwor1eln5GvsdXKr6JVuhjmtHcVSdi1N0BbbNVI5l9MYi7Uu4zPpjKei0Gp7q21jtOGbLpH1wli1bRlhYGH379uXOO++kW7dufPnll2XfLyoq4vjx42WrpBwcHPj777/p168fYWFhPPfccwwbNozffvut7DE6nY7Vq1ej0+mIjIzk4YcfZtSoUbz55pumfCtCqC+4EzS6QxnFke7GFml0l1C8Xew5k5bLqv0X1AkhozcW75O/lb4397StS31fV5XTmC+N0Wg0kyn9NScrKwtPT08yMzNlPo6wLBf2wle9QaOFJ3Yqy8iFRfl84yneX3OcBr6u/PVsD+x0NbhjTtEV+LSNUuAMngXtR9fca4tqsedsOsPmRqPTatjwXC9CatnW5OLKfH7LXlRCWJK67aDpnWA0wKb31E4jqmBU5LWjODU8F0dGbyzeJ2uV0Zv72gXZXHFTWVLgCGFpek1Tvh76GZKPqJtFVJqbox0TS3qWzF5/qua6GxfkXG0WKXNvLNLOM5fK+t5M6dNI7ThmTwocISxNndbQ7G7ACJveVTuNqIJRkfXwcXUgLi2XX/bW0FycnfMgLw2860P4QzXzmqJala6ceqBjsPS9qQApcISwRL2mARo48iskHVQ7jagkV0c7nijpXTLz7xMUFOtN+4JXLsP2Wcpx7/+TrsUWaPvpNHacScdBp2Vybxm9qQgpcISwRP7NoeW9yvGGGepmEVXycOd61PF0IjEzn293Jpj2xbbPVnYMr90cWg4z7WuJamc0Gvnwz+MADO8YTF0vZ5UTWQYpcISwVD1fVlZTHf8dzu+59fnCrDjZ68p6mMzZcIrcgmLTvFBOKuyYpxz3/j/Qyv/2Lc26oynsTcjAyV4rc28qQf6lC2Gp/JpcXQnz93SwvY4PFu++9kGE1nIhLaeQxdvjTfMiWz+GolwIbAdhg0zzGsJk9AYjH5SM3oztWl92DK8EKXCEsGS9XgadA8RvgdPr1U4jKslep+XZO5ReRvM2nSYzr6h6XyDzPOyarxz3eQU0mup9fmFyq/Zf4HhyNh5OdjwuO4ZXihQ4QlgyrxDoOEE5XvcGGGpoybGoNoNbBxIW4E52fjFfbK7mLTg2vQ/6QqjXDRr2qd7nFiZXWGzg47XKyqnHezXE00Umh1eGFDhCWLruU8HBHS7uhyMr1E4jKkmr1fBcv6YALNoWT0p2fvU8cdop2LdUOe77qozeWKDluxI4l34FP3dHxnapr3YciyMFjhCWztUXujypHK9/G/TVfJlDmFxUs9qEB3txpUjP7HWnqudJ172h7FvWuD+EdK6e5xQ1Jq+wmFkl/xae6tsYZwedyoksjxQ4QliDyMng4gvpZ2DfN2qnEZWk0Wh4aUAYAN/FJHAmNef2nvBcDBxdpayyi3r99gOKGrdoWzxpOQWE+LgwvEOw2nEskhQ4QlgDRzfo+aJyvPE9KMxTN4+otMiGtegTVptig5H31xyv+hMZjfDXq8px+ENKzyRhUS7nFjJvkzIf67l+TXCwk4/qqpCfmhDWov1YZdJxThLsnKt2GlEFLw8MQ6uBNYeT2B2fXrUnOf4/OLcD7Jyh13+qN6CoEbPWnyQ7v5hmdTwY3DpQ7TgWSwocIayFnQP0KfnNfcsnSoM3YVGa+LvzQMnliHf+dxRjZXsb6Yvh79eV48gnwLNu9QYUJheXlss30WcBeGVQM7RamRxeVVLgCGFNWt4HgW2hMBs2vqN2GlEFz97RBGd7HXsTMlhzKKlyD973DaSdAGcf6Pq0aQIKk3rvj2MUG4z0bupH10a+asexaFLgCGFNtFro91/leM9iSDmqahxRef4eTkzoriwJfm/NMYr0FextVJgLG0v2Jev5Ejh5miihMJWYuHTWHE5Cq4H/3NlM7TgWTwocIaxNaFcIuwuMhquTTYVFmdizIb5uDsRfyqv4RpzbP4OcZPAOhQ6PmjSfqH4Gg5H//n4EgBGdQmjs765yIssnBY4Q1uiON0FrB6fWyhYOFsjN0Y6no5QtHD5dd5Ks/Fv0Nsq8ANtmKsd9pyvzsYRFWX3wIvvPZ+LqoOPZkr97cXukwBHCGtVqCJ0mKsd/vgIGvbp5RKWN6BhMQz9X0nMLmb3u5M1P/vt1KMqDkEhocU+N5BPVJ79Iz3t/HANgUq+G+Lk7qpzIOkiBI4S16vECOHlBymGIXaZ2GlFJ9jotr96l9LBZtC2e0zdq/ncuBg7+AGhgwAzZksECLd4ez4WMKwR4ODGuWwO141gNKXCEsFYuPleb/61/Gwqy1c0jKq1X09plzf/eXn3k3ycYDPDHS8px25HKCjphUZKz8stG6F7o31S2ZKhGUuAIYc06TgCfBsrk003vq51GVMErg5phr9Ow4XgqG46llP/mge8hca+y2Wqf19QJKG7Le38cI7dQT9sQL+5pK32LqpMUOEJYMzsHGPCecrzjc0g9oW4eUWkN/NwY21VZNv7W70coLC5ZNl6Qc7WpX4/nwN1fnYCiyvacTeeXfRfQaOD1wS2kqV81kwJHCGvXpB80GQiGYvjjBWWvImFRnuzTCF83B86k5vJ1dLxy59ZPlG05vEOh8xNqxhNVoDcYmb7qMAAPtA+mTbCXuoGskBQ4QtiCAe+AzhHObISjv6mdRlSSu5M9L/ZXdhv/9O+TpJ8/DttnK9/s91+wk1U3lub7Xec4dCELdyc7XhjQVO04VkkKHCFsgU8D6PqUcvzn/8lu4xbovvZBtKrrSXZBEcnLnwJ9AdTvCWGD1I4mKikzr4gP/lSWhT8b1QRfNylQTUEKHCFsRbep4BkMmQlXm8IJi6HVanj97hb01+6iWc4ODFp7GPSRLAu3QB+vPc7lvCKa+LvxSGQ9teNYLSlwhLAVDi7Qv2Sfqq0zIT1O1Tii8toH2POe67cALLe/hyLvhionEpV1ODGTb3You4W/PrgF9jr5GDYV+ckKYUua3a1c1tAXwB8vyoRjS7PpXbyKUjhPbd7IvJOFW6VItSR6g5FpvxzEYIRBrevQRXYLNykpcISwJRoN3Pkh6Bzg5F9weIXaiURFJR+G6M8BiO/0OgU4MPPvk5y/LPOpLMU30fEcOJ+Ju5Md00u6VAvTMWmBk56ezsiRI/Hw8MDLy4tx48aRk3ODduNAfHw8Go3murcff/yx7LzrfX/58uWmfCtCWA+/JtD9OeX4j5fgymV184hbMxhg9VQw6iHsLroOfIiI+j5cKdLz+qrrdDgWZudi5hU++PM4AC8NCKO2h5PKiayfSQuckSNHcvjwYdauXcvq1avZvHkzEydOvOH5wcHBXLx4sdztjTfewM3NjYEDB5Y7d9GiReXOGzp0qCnfihDWpduz4NsEclNg7XS104hb2f8tnNsB9i4w4F00Gg3/vacl9joNfx9N5q/DSWonFLfw+qrD5BbqaRfixUOdQtSOYxNMVuAcPXqUNWvWMH/+fCIiIujWrRuzZ89m+fLlJCYmXvcxOp2OgICAcrcVK1bwwAMP4ObmVu5cLy+vcuc5OUk1LESF2TnCXTOV471L4Ox2VeOIm8hOVpb2A/R6GbyCAWhU250J3ZWNGV9fdZjcgmK1Eopb+OtwEn8eTsZOq+Gde1tJx+IaYrICJzo6Gi8vLzp06FB2X1RUFFqtlp07d1boOfbs2UNsbCzjxo371/cmT56Mr68vnTp1YuHChRhvMlmyoKCArKyscjchbF5oV2g3Wjn+7WkoLlA3j/g3oxF+nwr5GVCnzb86Fj/ZpzHBPs4kZubz3ppj6mQUN5VTUFzWsXhCjwaEBXionMh2mKzASUpKonbt2uXus7Ozw8fHh6Skig2nLliwgGbNmtGlS5dy97/55pv88MMPrF27lmHDhvHEE08we/bsGz7PjBkz8PT0LLsFBwdX/g0JYY3ueANca0PaCaX1vzAvR1bCsdWgtYMhc0BnX+7bzg463r23NQBfR58l+vQlFUKKm/nwz+NczMwnxMeFp/o0VjuOTal0gfPyyy/fcCJw6e3Ysdv/TeLKlSt8++231x29efXVV+natStt27blpZde4sUXX+SDDz644XNNmzaNzMzMstu5c+duO58QVsHZGwaWbMa55SNIlgmrZiP3EvzvBeW421QIaHXd07o28uXBkjkdL/18gLxCuVRlLnacucTi7fEAvD20Jc4OOnUD2ZhKFzjPPfccR48evemtQYMGBAQEkJKSUu6xxcXFpKenExAQcMvX+emnn8jLy2PUqFG3PDciIoLz589TUHD9IXZHR0c8PDzK3YQQJVrco2zGqS+EFY+BvkjtRAJgzcuQmwp+zaDH8zc99T93hhHo6URCel7ZSh2hrtyCYl74aT8AD3YKpkcTP5UT2R67yj7Az88PP79b/0VFRkaSkZHBnj17aN++PQDr16/HYDAQERFxy8cvWLCAu+++u0KvFRsbi7e3N46Osp+HEJWm0cDgmfD5Dkg6AJs/hN7T1E5l246vgYM/gEarXJq6xWaa7k72zBjWmtELY1i8PZ47W9WhY6hPDYUV1zPjj6OcS79CXS9n/m+Q9LxRg8nm4DRr1owBAwYwYcIEYmJi2LZtG1OmTGHEiBEEBgYCcOHCBcLCwoiJiSn32FOnTrF582bGjx//r+f97bffmD9/PocOHeLUqVPMnTuXd955hyeffNJUb0UI6+ceoOxrBLD5A0jcp24eW3YlA1Y/qxxHToag9hV6WM8mfjzQIQijEV786QBXCvWmyyhuauvJNJbuSADgg/ta4+ZY6bEEUQ1M+lNftmwZU6ZMoW/fvmi1WoYNG8asWbPKvl9UVMTx48fJyyvfiXPhwoUEBQXRr1+/fz2nvb09c+bM4dlnn8VoNNKoUSM+/vhjJkyYUO359Xo9RUUyXG8OHBwc0Gql8bZJtRwGR39TuhuveBwmbgJ7ab9Qo0pXTWUnKjvA9/pPpR7+f4Oas+lEKnFpuXz413FelW65NS47v4gXSy5NjYqsJ9sxqEhjvNn6aiuVlZWFp6cnmZmZ152PYzQaSUpKIiMjo+bDievSarXUr18fBwcHtaNYt9xL8HlnpQFglyeh39tqJ7It+7+HFRNBo4Nxf0FQh1s/5h82HEth7OJdAHwzrhPdG8vcj5r00k8H+H73OUJ8XPjj6e64yuhNtbrV5/e15Cd/HaXFTe3atXFxcUGjkaZMajIYDCQmJnLx4kVCQkLk78OUXGvB3bPguxGw/TNoeifU63Lrx4nbdzkefi/ZQqPXy1UqbgB6h9Xmkc71+GbHWab+sJ81T3enlpvMT6wJfx1O4vvd59Bo4MP720hxozL56f+DXq8vK25q1aqldhxRws/Pj8TERIqLi7G3t7/1A0TVNR0I4Q9D7FL4ZSI8vkVZTi5MR18MvzwGhdkQ3FlZFn4b/m9QM3acucTJlBxe+vkAX43qIL8YmFhixhVe+OkAAOO71adTfZnkrTaZ1PAPpXNuXFxcVE4irlV6aUqvl4mTNWLADPCuD5nn4NcpytwQYTpbP1H2mnJwh3u/AN3t/e7pZK9j1oNtcdBp+ftoCkt3nK2moOJ6ivUGnlkeS+aVIloHefJC/zC1IwmkwLkh+W3HvMjfRw1z8oD7FoLWXumku2u+2oms1/ndsHGGcjzoI/AOrZanbVbHg5cGKh+0b/9+lBPJ2dXyvOLfZq8/RUx8Om6Odsx+sC0OdvLRag7kb0EIcX1120G/t5TjP/8DF/erm8ca5aXDT2PBqFdWsbV+oFqffmyXUHo28aOg2MBT3+0jv0hGQKvbjjOXmL3+JAD/vacl9Wq5qpxIlJICx4ZoNBpWrlypdgxhSSIeVyYa6wvhx7FQIKMA1cZgUDpHZyQoozaDPlaaLlYjrVbDh/e3oZarA8eSsnnt10M33ZhYVM7l3EKeWR6LwQj3tQ9iSHhdtSOJa0iBY0VSU1OZNGkSISEhODo6EhAQQP/+/dm2bRsAFy9eZODAgSqnFBZFo1E66XoEQfppWD1V5uNUly0fwcm/wM4JHvgGnL1M8jJ+7o58OqItWg38sPs8y3fJXnzVQW8wMvWHWJKy8mng58obd7dQO5L4BylwrMiwYcPYt28fS5Ys4cSJE6xatYpevXpx6ZKyw3BAQIBsZyEqz8UH7lug9GY5+IPMx6kOp9bBhv8qx4M+hjqtTfpy3Rr78ly/pgBM//UwsecyTPp6tuCTtSfYcDwVRzstsx9sK0vCzZAUOFYiIyODLVu28N5779G7d2/q1atHp06dmDZtGnfffTdQ/hJVfHw8Go2GX375hd69e+Pi4kKbNm2Ijo4ue87XX3+d8PDwcq8zc+ZMQkNDy/68ceNGOnXqhKurK15eXnTt2pWzZ2XFhtUJ6QxRryvHa16GuC2qxrFoGefg5/GAEdqNhrYja+Rln+jVkH7N/SnUG3hi6R4u5Vx/c2Jxa/87eJHPNpwC4L1hrWkR6KlyInE9UuBUgNFoJK+wuMZvlblW7ubmhpubGytXrrzhrurX83//9388//zzxMbG0qRJEx588EGKi4sr9Nji4mKGDh1Kz549OXDgANHR0UycOFFWPFmrLk9CqwfAUAw/jILLUshWWnEB/DgarqRDnTYw8P0ae2mNRsOHD7Shga8riZn5PPndPor1hhp7fWtxLCmL539UJtyP71afoW1l3o25kjG1CrhSpKf5a3/W+OseebM/Lg4V+yuys7Nj8eLFTJgwgXnz5tGuXTt69uzJiBEjaN36xsPfzz//PIMGDQLgjTfeoEWLFpw6dYqwsFv3ccjKyiIzM5O77rqLhg0bAsomq8JKaTRKl+O0E3AxFpY/BI/+CY5uaiezDEaj0lPowh5w8oIHvq7xvb48nOyZ90h7hs7ZxvbTl3hvzTHZ6boSMvIKmfj1HvIK9XRtVIuXB0q/G3MmIzhWZNiwYSQmJrJq1SoGDBjAxo0badeuHYsXL77hY64tfurUqQNASkpKhV7Px8eHMWPG0L9/fwYPHsynn37KxYsXb+s9CDNn7wwjvgXX2pB8CFZOkknHFbXxXWUOk0YH9y+qtn43ldXE353371P+u/9qSxzLdspIXEUU6w08+d0+EtLzCPJ25rMH22Gnk49QcyYjOBXgbK/jyJv9VXndynJycuKOO+7gjjvu4NVXX2X8+PFMnz6dMWPGXPf8a7c9KL20ZDAow9ZarfZfl8n+ubv6okWLeOqpp1izZg3ff/89r7zyCmvXrqVz586Vzi4shGddGL4UFg+Co6uUD+7e09ROZd72fw+b3lWO7/oYGvZRNc5drQM5lZLDzL9P8urKQwR6OtM7rLaqmcyZ0Wjk1V8Ps+VkGk72Wr58pAPerrLxr7mT8rMCNBoNLg52NX6rjrkszZs3Jzc3t0qP9fPzIykpqVyRExsb+6/z2rZty7Rp09i+fTstW7bk22+/rWpcYSlCIpQPalA+uHcvUjePOYvfBr9OVo67PgPtx6iZpszTfRtzX/sgDEaY/O1eDl3IVDuS2Zq17hTfxSSg0cDM4eE0D7z5LtbCPEiBYyUuXbpEnz59WLp0KQcOHCAuLo4ff/yR999/nyFDhlTpOXv16kVqairvv/8+p0+fZs6cOfzxxx9l34+Li2PatGlER0dz9uxZ/vrrL06ePCnzcGxFu1HQ4wXl+PepcGSVunnMUdop+H4kGIqg+RDoO13tRGU0Gg3v3NOKro1qkVeoZ+ziXVzIuKJ2LLOzPCaBT/4+AcCbd7dgQMs6KicSFSUFjpVwc3MjIiKCTz75hB49etCyZUteffVVJkyYwGeffVal52zWrBmff/45c+bMoU2bNsTExPD888+Xfd/FxYVjx44xbNgwmjRpwsSJE5k8eTKPPfZYdb0tYe56/5+y1NloUJY+x29VO5H5yDwPS++FK5ehbge45wvQmtf/ch3stMx9uD1N/d1JzS5g7KIYMvOKbv1AG/H3kWT+s+IgAFN6N+KRyFB1A4lK0RhtsG93VlYWnp6eZGZm4uFRfqgxPz+fuLg46tevj5NTza5wEDcmfy9mTF+sLH0+thocPWDs/yCgldqp1JWdBIvuVLo/+zRQVpu5me8clwsZV7hnzjZSsgtoE+TJN+Mj8HCyv/UDrdies5cZOX8H+UUG7m8fxPv3tZYWGGbgZp/f/2Rev04IISyPzg6GzYeQLlCQBUuHQdpJtVOpJzcNvh6iFDeeITBqlVkXNwB1vZz5elwnvF3s2X8+k9ELY8jOt92RnH0JlxmzKIb8IgO9m/rxzr2tpLixQFLgCCFun70zPPgd+LeEnGRl9CLlqNqpal5eOnw9FFKPgXsgjF4FXsFqp6qQsAAPlo6PwNPZnn0JGYxdtIvcgoo1/bQme86m88iCGLLzi+kU6sOcke2wl+XgFkn+1oQQ1cPZCx5ZqRQ5uSnKMvKLB9ROVXOuZCijV8kHlT5Bo38Dn/pqp6qUFoGeLBsfgYeTHbvPXmbs4l3kFdpOkbMrPp1RC2LIKSimcwMfFj/ascLNVoX5kQJHCFF93PyUD/Y64ZB3CZbcpXTutXY5Kcp7TdwLzj4w6lfwbaR2qippWdeTb8ZF4O5oR0xcOmMW7SLLBi5X7ThzidELY8gt6VK8aEwnKW4snBQ4Qojq5eKjXJoJ6gT5mbBkCCTsUDuV6WQkwMIBkHQQXP2U9+5v2dsftAn2Ysm4TmVFzogvdpCabb2bc244lsLYRbvIK9TTvbEvC0Z3xNmh8o1WhXmRAkcIUf2cPOGRX6BeNyjMVibdHl6pdqrql7gP5keVTCgOVlZLWckKsnYh3nw3sTO+bg4cuZjFffO2czo1R+1Y1W55TALjv97NlSI9PZv48dWoDjhVoYu8MD9S4AghTMPRHUb+CE0GQHG+spR826fWs3fVsf8pk6lzkqF2C6W4qdVQ7VTVqmVdT358vAtB3s6cvZTHvZ9vZ/vpNLVjVQu9wch7a47x8i8H0RuM3NuurhQ3VkYKHCGE6Ti4KJtzdpyg/Hnta/DLBCjMUzfX7TAYYON7ym7qRXnQoDc8ukbZo8sK1fd1ZcUTXWkb4kXmlSJGLYjh6+j4f+1TZ0my8ouY8PVu5m48DShN/D66vw0OdvKRaE3kb1MIYVpaHdz5AQx4T9lJ++CPsLAfXDqtdrLKy0tXtl7Y+A5ghA7jlFEqJ+vem8jP3ZHvJnRmcJtAig1GXvv1MFN/2G+RK6wOJ2Yy9LNtrD+WgqOdlpnDw3m+f1Ppc2OFpMARFRIaGsrMmTPVjiEslUYDnR9XVhe5+CoTcr/ooeyybSnObod53eH4/0DnAHd/pmw4qrONjr9O9jpmjQjnlUHN0Gk1rNh3gcGzt1rMJp1Go5FvouO55/PtnEnLpY6nEz8+HsnQttY58iakwLEqY8aMYejQoeXu++mnn3BycuKjjz66refetWsXEydOvK3nEIL63eGxzVCvKxTmwIqJ8OMYpfuvuSrKh7XTlb4+Weevbr3Q7hG1k9U4jUbD+O4NWDY+gtrujpxOzeWez7cxZ8MpivQGtePd0MXMK4xetItXfz1MYbGBvmG1+d9T3Wkd5KV2NGFCUuBYsfnz5zNy5Ejmzp3Lc889d1vP5efnh4uLSzUlEzbNs67SK6fXf5RLVodXwJxOymiOuc3riN8G87rBtpnKhqKtRygFWt12aidTVecGtfjzmR70b+FPkd7IB38e5+7PtnHgfIba0crRG5RRm36fbGbziVQc7LS8MqgZ80d3wNvVQe14wsSkwLFS77//Pk8++STLly9n7NixAMydO5eGDRvi4OBA06ZN+eabb8rONxqNvP7664SEhODo6EhgYCBPPfVU2ff/eYlKo9Ewf/587rnnHlxcXGjcuDGrVq0q+/7ixYvx8vIql2nlypXlrnPv37+f3r174+7ujoeHB+3bt2f37t3V/JMQZkmrg14vwYR1SufjvEvKaM7CAZAYq3Y6ZSfwnx6FxXfCpZPgFqBMlr73C2V1mMDb1YF5D7fnw/vb4Olsz9GLWQyZs42XfjpASna+2vGIiUtnyJytvPrrYbLzi2kT7MX/nurO+O4NZL6NjZA2jRVhNCqrJWqavYsyd6GSXnrpJT7//HNWr15N3759AVixYgVPP/00M2fOJCoqitWrVzN27FiCgoLo3bs3P//8M5988gnLly+nRYsWJCUlsX///pu+zhtvvMH777/PBx98wOzZsxk5ciRnz57Fx8enQjlHjhxJ27ZtmTt3LjqdjtjYWOztbWM+gygR2BYmbIDts2DLR3BuB3zZE1rcA72mgV/Tms2TnQxbP4HdC0FfAGig/RiImg7O3jWbxQJoNBruax9Er6Z+vLX6CL/GJvL97nOsPpDImK6hjO/WoMZHSg5dyOSjv46z4XgqAO5OdrzQvykjI+qh00phY0tMVuD897//5ffffyc2NhYHBwcyMjJu+Rij0cj06dP56quvyMjIoGvXrsydO5fGjRuXnZOens6TTz7Jb7/9hlarZdiwYXz66ae4ubmZ6q0oxc07gaZ7/hv5TyI4uFbqIX/88Qe//vor69ato0+fPmX3f/jhh4wZM4YnnngCgKlTp7Jjxw4+/PBDevfuTUJCAgEBAURFRWFvb09ISAidOnW66WuNGTOGBx98EIB33nmHWbNmERMTw4ABAyqUNSEhgRdeeIGwsDCAcn/PwobYOUCP56HNg/D3dGWV1eEVSmPApndC5BPKnB1T/tadcgx2fA4Hvld69oDSpHDAO1Cnjele10r4ujny6Yi2jIqsx5urj7L/XAZzNpxm8bZ4hncM4ZHIetT3rdz/yyrDYDCy9VQaX205w5aTynwunVbDAx2CmXpHE/zcHU322sJ8mewSVWFhIffffz+TJk2q8GPef/99Zs2axbx589i5cyeurq7079+f/Pyrw50jR47k8OHDrF27ltWrV7N582aZ/HqN1q1bExoayvTp08nJudp19OjRo3Tt2rXcuV27duXoUWXH5/vvv58rV67QoEEDJkyYwIoVKyguvvkS0NatW5cdu7q64uHhQUpKSoWzTp06lfHjxxMVFcW7777L6dMWuGxYVB/PujBsPkzaDmF3AUY4/rsyuXdOBGz5GC6frb7Xy70EuxfBgn7weQTsXaIUN3U7KJuGjlktxU0lta/nw4pJXfjikfa0CPQgt1DPwm1x9P5wIw/P38kPu89V675Wp1Jy+PTvk/T4YAOjFsaw5WQaWg3c3SaQtc/2YMa9raS4sWEmG8F54403AGUuRkUYjUZmzpzJK6+8wpAhQwD4+uuv8ff3Z+XKlYwYMYKjR4+yZs0adu3aRYcOHQCYPXs2d955Jx9++CGBgSYaZbF3UUZTapp95Sf11q1bl59++onevXszYMAA/vjjD9zdbz1nIDg4mOPHj/P333+zdu1annjiCT744AM2bdp0w8tG/7xfo9FgMCgrKbRa7b8agRUVlf8f2+uvv85DDz3E77//zh9//MH06dNZvnw599xzT2XesrA2/i1gxDJIPQ475sL+5ZB2HNa9odz8mkHjKAiOUIoR94CKje5cuQwX9sL5XXB6vfLVWLLyR6MtGS2aDCGRph0tsnJarYb+LQLo19yfTSdSWbI9no0nUtl6Ko2tp9L4vxUHaRfiTY8mfrQN8aJlXU88nG59adpoNJKYmU9sQga74tPZfDKVM6m5Zd93d7RjWPsgxnWrT7CPLIgQZjQHJy4ujqSkJKKiosru8/T0JCIigujoaEaMGEF0dDReXl5lxQ1AVFQUWq2WnTt33vCDsaCggIKCqxvFZWVlVS6cRlPpS0VqqlevHps2bSorctasWUOzZs3Ytm0bo0ePLjtv27ZtNG9+dVNAZ2dnBg8ezODBg5k8eTJhYWEcPHiQdu0qv2LEz8+P7OxscnNzcXVVfnaxsbH/Oq9JkyY0adKEZ599lgcffJBFixZJgSMUfk1h8Ey440048qtS6CRsh9Sjyo3ZynmOnlCrgTIR2MUH7J0BjTKHJi8dclMh/Yzy9Z/8W0Hr+6HVA+BRpwbfnPXTaDT0alqbXk1rk3Apj1X7L7AyNpFTKTnsjEtnZ1x62bn+Ho4Ee7tQ28MRd0d7nOy1FBuMFBQbSM8tJCU7n7jUXHIL9eVew16nIbKhL0PDAxnYso5skCnKMZsCJykpCQB/f/9y9/v7+5d9Lykpidq1a5f7vp2dHT4+PmXnXM+MGTPKRpRsRXBwMBs3bqR3797079+fxx9/nPHjx9O2bVuioqL47bff+OWXX/j7778BZaRNr9cTERGBi4sLS5cuxdnZmXr16lXp9Uuf5z//+Q9PPfUUO3fuLDead+XKFV544QXuu+8+6tevz/nz59m1axfDhg2rjrcvrImTh9Jzpt0jSsFyej3Eb4FzuyDlCBRkKpteVoR3qLLLeUhnaNwPvIJNGl0oQmq5MKVPY6b0aUx8Wi5bTqYSfeYSB85ncv7yFZKzCkjOuvVu5XZaDY393ekU6k2n+rXo0cQX9wqM/gjbVKkC5+WXX+a999676TlHjx4tmzRqLqZNm8bUqVPL/pyVlUVwsPX/jy0oKKisyJk7dy4ffPABH374IU8//TT169dn0aJF9OrVCwAvLy/effddpk6dil6vp1WrVvz222/UqlWrSq/t4+PD0qVLeeGFF/jqq6/o27cvr7/+etl8KZ1Ox6VLlxg1ahTJycn4+vpy77332lwhKirJxQda3afcQGnCdzlO2fYhNxWupENxyQel1h6cvcClFvjUB5+GVr+lgiUI9XUl1NeVRyJDAcjIK+TspTwS0vNIzy0kp6CY/CI9Oq0Ge52WWq4O+Lo5Uq+WC6G+rtjrpLuJqBiNsRI7pqWmpnLp0qWbntOgQQMcHK4uC1y8eDHPPPPMLVdRnTlzhoYNG7Jv3z7Cw8PL7u/Zsyfh4eF8+umnLFy4kOeee47Lly+Xfb+4uBgnJyd+/PHHCl/ayMrKwtPTk8zMTDw8yv8PLz8/n7i4OOrXr4+Tk1OFnk+Ynvy9CCGEuNnn9z9VagTHz88PPz+/2wp3I/Xr1ycgIIB169aVFThZWVns3LmzbCVWZGQkGRkZ7Nmzh/bt2wOwfv16DAYDERERJsklhBBCCMtjsrG+hIQEYmNjSUhIQK/XExsbS2xsbLmly2FhYaxYsQJQJqQ988wzvP3226xatYqDBw8yatQoAgMDy/ZXatasGQMGDGDChAnExMSwbds2pkyZwogRI0y3gkoIIYQQFsdkk4xfe+01lixZUvbntm3bArBhw4ayeR/Hjx8nM/PqTrQvvvgiubm5TJw4kYyMDLp168aaNWvKXZJYtmwZU6ZMoW/fvmWN/mbNmmWqtyGEEEIIC1SpOTjWQubgWB75exFCCFGZOTgyHV0IIYQQVkcKnBso7cgrzIMNDjQKIYS4DWbT6M9cODg4oNVqSUxMxM/PDwcHBzTStl1VRqOR1NRUNBqN7DYuhBCiQqTA+QetVkv9+vW5ePEiiYkq7D8lrkuj0RAUFIROJ63YhRBC3JoUONfh4OBASEgIxcXF6PX6Wz9AmJy9vb0UN0IIISpMCpwbKL0cIpdEhBBCCMsjk4yFEEIIYXWkwBFCCCGE1ZECRwghhBBWxybn4JT2VMnKylI5iRBCCCEqqvRzuyK90WyywMnOzgYgODhY5SRCCCGEqKzs7Gw8PT1veo5N7kVlMBhITEzE3d292pv4ZWVlERwczLlz5265T4atkZ/NzcnP5+bk53Nz8vO5MfnZ3Jwl/XyMRiPZ2dkEBgai1d58lo1NjuBotVqCgoJM+hoeHh5m/w9FLfKzuTn5+dyc/HxuTn4+NyY/m5uzlJ/PrUZuSskkYyGEEEJYHSlwhBBCCGF1pMCpZo6OjkyfPh1HR0e1o5gd+dncnPx8bk5+PjcnP58bk5/NzVnrz8cmJxkLIYQQwrrJCI4QQgghrI4UOEIIIYSwOlLgCCGEEMLqSIEjhBBCCKsjBU41mjNnDqGhoTg5OREREUFMTIzakczG5s2bGTx4MIGBgWg0GlauXKl2JLMxY8YMOnbsiLu7O7Vr12bo0KEcP35c7VhmY+7cubRu3bqsCVlkZCR//PGH2rHM0rvvvotGo+GZZ55RO4pZeP3119FoNOVuYWFhascyKxcuXODhhx+mVq1aODs706pVK3bv3q12rGohBU41+f7775k6dSrTp09n7969tGnThv79+5OSkqJ2NLOQm5tLmzZtmDNnjtpRzM6mTZuYPHkyO3bsYO3atRQVFdGvXz9yc3PVjmYWgoKCePfdd9mzZw+7d++mT58+DBkyhMOHD6sdzazs2rWLL774gtatW6sdxay0aNGCixcvlt22bt2qdiSzcfnyZbp27Yq9vT1//PEHR44c4aOPPsLb21vtaNXDKKpFp06djJMnTy77s16vNwYGBhpnzJihYirzBBhXrFihdgyzlZKSYgSMmzZtUjuK2fL29jbOnz9f7RhmIzs729i4cWPj2rVrjT179jQ+/fTTakcyC9OnTze2adNG7Rhm66WXXjJ269ZN7RgmIyM41aCwsJA9e/YQFRVVdp9WqyUqKoro6GgVkwlLlJmZCYCPj4/KScyPXq9n+fLl5ObmEhkZqXYcszF58mQGDRpU7v9BQnHy5EkCAwNp0KABI0eOJCEhQe1IZmPVqlV06NCB+++/n9q1a9O2bVu++uortWNVGylwqkFaWhp6vR5/f/9y9/v7+5OUlKRSKmGJDAYDzzzzDF27dqVly5ZqxzEbBw8exM3NDUdHRx5//HFWrFhB8+bN1Y5lFpYvX87evXuZMWOG2lHMTkREBIsXL2bNmjXMnTuXuLg4unfvTnZ2ttrRzMKZM2eYO3cujRs35s8//2TSpEk89dRTLFmyRO1o1cImdxMXwlxNnjyZQ4cOyTyBf2jatCmxsbFkZmby008/MXr0aDZt2mTzRc65c+d4+umnWbt2LU5OTmrHMTsDBw4sO27dujURERHUq1ePH374gXHjxqmYzDwYDAY6dOjAO++8A0Dbtm05dOgQ8+bNY/To0Sqnu30yglMNfH190el0JCcnl7s/OTmZgIAAlVIJSzNlyhRWr17Nhg0bCAoKUjuOWXFwcKBRo0a0b9+eGTNm0KZNGz799FO1Y6luz549pKSk0K5dO+zs7LCzs2PTpk3MmjULOzs79Hq92hHNipeXF02aNOHUqVNqRzELderU+dcvCc2aNbOay3hS4FQDBwcH2rdvz7p168ruMxgMrFu3TuYJiFsyGo1MmTKFFStWsH79eurXr692JLNnMBgoKChQO4bq+vbty8GDB4mNjS27dejQgZEjRxIbG4tOp1M7olnJycnh9OnT1KlTR+0oZqFr167/aklx4sQJ6tWrp1Ki6iWXqKrJ1KlTGT16NB06dKBTp07MnDmT3Nxcxo4dq3Y0s5CTk1Put6a4uDhiY2Px8fEhJCRExWTqmzx5Mt9++y2//vor7u7uZfO2PD09cXZ2Vjmd+qZNm8bAgQMJCQkhOzubb7/9lo0bN/Lnn3+qHU117u7u/5qr5erqSq1atWQOF/D8888zePBg6tWrR2JiItOnT0en0/Hggw+qHc0sPPvss3Tp0oV33nmHBx54gJiYGL788ku+/PJLtaNVD7WXcVmT2bNnG0NCQowODg7GTp06GXfs2KF2JLOxYcMGI/Cv2+jRo9WOprrr/VwA46JFi9SOZhYeffRRY7169YwODg5GPz8/Y9++fY1//fWX2rHMliwTv2r48OHGOnXqGB0cHIx169Y1Dh8+3Hjq1Cm1Y5mV3377zdiyZUujo6OjMSwszPjll1+qHanaaIxGo1Gl2koIIYQQwiRkDo4QQgghrI4UOEIIIYSwOlLgCCGEEMLqSIEjhBBCCKsjBY4QQgghrI4UOEIIIYSwOlLgCCGEEMLqSIEjhBBCCKsjBY4QQgghrI4UOEIIIYSwOlLgCCGEEMLqSIEjhBBCCKvz/4HOcRB/0arEAAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"plt.plot(x, s, label=\"Sinus\") # Plotte Sinus mit label Sinus\n",
|
||
"plt.plot(x, c, label=\"Kosinus\") # Plotte Kosinus mit label Kosinus\n",
|
||
"plt.legend() # Füge die Legende ein\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "fb03ce2f-5639-402a-9b32-0b351113b5d6",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-63bbc82ff5e6892a",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Linestyle\n",
|
||
"\n",
|
||
"Eine weitere wichtige Eigenschaft beim Plotten ist das Festlegen des **Linestyles**. \n",
|
||
"\n",
|
||
"Dazu wird dem Aufruf von `plt.plot` der Parameter `linestyle` als String übergeben. Die verschiedenen verfügbaren Linestyles können der Dokumentation zu [Linestyles](https://matplotlib.org/stable/gallery/lines_bars_and_markers/linestyles.html) entnommen werden. \n",
|
||
"\n",
|
||
"Beispiel; Den Sinus als **dashed** Linie darstellen:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 36,
|
||
"id": "90be449a-1d18-416f-b22b-782081d1b007",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-402e40ea2ceafc35",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAVS9JREFUeJzt3XlcVPX+P/DXzAAz7IvssiquqaCgiEtpcsWy0vKadi2XTH+ZVkZlcW9pZWWLt8zyZotraVrdtNLCELdUFEUxd0XZ90Vm2JeZ8/sDmy5fRUEZPrO8no/HedzmcM7hdcYL8+ZzPotMkiQJRERERGZELjoAERERUXtjgUNERERmhwUOERERmR0WOERERGR2WOAQERGR2WGBQ0RERGaHBQ4RERGZHRY4REREZHasRAcQQafTIS8vD46OjpDJZKLjEBERUStIkoSKigr4+vpCLr9xG41FFjh5eXnw9/cXHYOIiIhuQXZ2Nvz8/G54jEUWOI6OjgCa3iAnJyfBaYiIiKg1NBoN/P399Z/jN2KRBc6fj6WcnJxY4BAREZmY1nQvYSdjIiIiMjsscIiIiMjssMAhIiIis8MCh4iIiMwOCxwiIiIyOyxwiIiIyOywwCEiIiKzwwKHiIiIzA4LHCIiIjI7Bi1w9u3bh/vvvx++vr6QyWTYunXrTc/Zs2cPBgwYAKVSiZCQEKxdu/aaY1asWIGgoCCoVCpERkYiOTm5/cMTERGRyTJogVNVVYXQ0FCsWLGiVcenp6dj7NixGDlyJFJTUzF//nw88cQT2LFjh/6YzZs3IzY2FosWLcKxY8cQGhqKmJgYFBUVGeo2iIiIyMTIJEmSOuQbyWTYsmULxo8f3+IxL730ErZv345Tp07p902ePBnl5eWIj48HAERGRmLgwIH45JNPAAA6nQ7+/v54+umn8fLLL7cqi0ajgbOzM9RqNdeiIiIiMhFt+fw2qsU2k5KSEB0d3WxfTEwM5s+fDwCor69HSkoK4uLi9F+Xy+WIjo5GUlJSi9etq6tDXV2d/rVGo2nf4GSSahu0SC+pQnpJFfr5OcPP1Q4AcL6gAj8cz4Gj0goudjbwc7VFgJsdAjvZQyG/+QJvREQknlEVOAUFBfDy8mq2z8vLCxqNBjU1Nbhy5Qq0Wu11jzl37lyL112yZAlef/11g2Qm01FV14h9F4qRdLkUyelluFBYAd3V9st/TwyFX3hTgZNbXo3P9l6+5nx7GwXu6OyMmcOCEXOHd0dGJyKiNjKqAsdQ4uLiEBsbq3+t0Wjg7+8vMBF1tN8vFmPmuqOob9Q12++oskKIpwMcVH/9KAS7O+CJYcGorGtESWU9cq5UI6O0ClX1WiSnl2FaVJD+2Hx1DbJKqzEo2A0yGVt3iIiMhVEVON7e3igsLGy2r7CwEE5OTrC1tYVCoYBCobjuMd7eLf9FrVQqoVQqDZKZjFORphZXqhvQw9sRAHCHrzMatToEdbLDiB6eGBjkhgGBLvB2Ul1TmAS72+OV+3o326fVSbhUXInUrHIMC3HX7//2SA4+3HkB3TwdMDUqEBPC/WBnY1Q/VkREFsmofhNHRUXhl19+abYvISEBUVFRAAAbGxuEh4cjMTFR31lZp9MhMTER8+bN6+i4ZITy1TVYnpiG/6bkoK+fM/47ZwgAwM3eBntfHAk/V9tbamlRyGXo7uWI7l6O13zN3kaBi0WVePXH01i28yJm39kFjw4OhL3SqH68iIgsikF/A1dWViItLU3/Oj09HampqXBzc0NAQADi4uKQm5uL9evXAwCefPJJfPLJJ1iwYAEef/xx7Nq1C99++y22b9+uv0ZsbCymTZuGiIgIDBo0CMuWLUNVVRVmzJhhyFshI1dR24BPdqVh7cEM1F19DCWXNe13VFkDAPzd7Nr9+z4b3Q0zhgXhh5QcrDqQjuyyGiz59RxW7U/HizE9MDGCj0KJiEQwaIFz9OhRjBw5Uv/6z34w06ZNw9q1a5Gfn4+srCz914ODg7F9+3Y899xz+Oijj+Dn54cvv/wSMTEx+mMmTZqE4uJiLFy4EAUFBQgLC0N8fPw1HY/JMkiShJ9O5OHN7WdRXNE0Um5QkBteiOmBQcFuHZLBSWWN6UODMWVwILYez8XyXReRXVaDg5dKWeAQEQnSYfPgGBPOg2M+tv+Rj7kbjwEAgjrZYeH9vTGyh6fQDr91jVqsP5iJ+0J94ONsCwAor66HyloBlbVCWC4iIlNnsvPgELXVmD7eGNK1E6K6dMLsu7pAaSW+gFBaKTDrzi7N9v1zy0mkFVVi2aT+6O3LopqIyNC42CaZlJp6LT7aeRG1DVoATZ1/v54ZiadHdTOK4uZ6SivrkJx+BRcKKzF+xQGsO5gBC2w4JSLqUCxwyGRklVZj/IoD+HDnBbz9y1n9frmRzy7cyUGJ+PnDEd3LE/VaHRb9dBrPbU5FdX2j6GhERGaLBQ6ZhANpJXhgxX6cL6yAu4MSY0xsJmF3ByW+mBqBV8b2gkIuw9bUPDz0n4PILa8RHY2IyCyxwCGjtyk5C1NXJ6O8ugGh/i7Y/swwDPmfyfZMhUwmwxPDu2DjE5Fwd1DiXEEFZq49Ap2Oj6uIiNobCxwyWpIk4YOEC3j5h5PQ6iQ81L8zNs8eDC8nlehotyWySydsnTsEoX7OeOvBPkb/iI2IyBRxFBUZrZwrNVi9Px0A8MyobnguupvZrPfk52qHrXOHNrufsqp6uNnbCExFRGQ+2IJDRsvfzQ5rZgzEOw/1RezfuptNcfOn/72fU7lq3PX+bnx9KFNgIiIi88EWHDIqjVodcstrENjJHgAwMMgNA4M6ZkZikRLOFKKithGvbD0FK7kMkwcFiI5ERGTS2IJDRkOnk/DCdycwbsUB/JFTLjpOh5of3Q2PDw0GAMRtOYnvjmYLTkREZNrYgkNGQZIk/GvrKWxNzYOVXKZfV8pSyGQyvHpfL2h1OqxLysSC//4BK4UMD/b3Ex2NiMgksQWHhJMkCW9tP4tvkrMglwEfTgrDqF6Wt3iqTCbDaw/cgSmRAZAk4PlvT+CnE3miYxERmSQWOCTcsp0X8eXV0VLvPNQP94f6Ck4kjkwmw+JxfTB5oD90EvDN4SzOk0NEdAv4iIqE+iopAx8lXgQAvHZ/bzw80F9wIvHkchnefrAvevs64eEIf86TQ0R0C9iCQ8JodRJ+PpEPAHj+b90x/WonW2oqcqZGBUFl/dcCon8uMEpERDfHFhwSRiGXYf3MQdhyPBeT2XLTIp1Owns7zmN/WjE2z46CvZI/tkREN8MWHOpwdY1/tUSorBV4ZFCA2U3i155KKuvw3dFsnMrVYN7GY2jU6kRHIiIyeixwqEPVNmjxjy8O4734c+w820qeTip8OS0CKms5dp8vxtu/nBMdiYjI6LHAoQ4jSRLifjiJlMwr+PpQJvI1taIjmYz+Aa5YNikMALD6QDqHjxMR3QQLHOowXx/KxJbjuVDIZfj00XB0drEVHcmkjOnjg6dGdAUAvPT9HzhfUCE4ERGR8WKBQx0iNbscb2w7AwCIu6cnhoa4C05kmp4f3QPDu7mjpkGLJ79O4cgqIqIWsMAhg7tSVY+5G46hQSsh5g4vzBzG4eC3SiGX4aPJ/dHN0wHzo7s1G0ZORER/4XhTMihJkhD7berVFcLt8P7EUI6Yuk1u9jb49dnhsFLw7xMiopbwNyQZlEwmw/2hvnC1s8Z/pgyAk8padCSz8L/FTWllHU7nqQWmISIyPmzBIYN7aIAfYu7w5gR1BnA6T43pa47ARiHHL88Oh7MtC0giIoAtOGQgmtoGlFfX61+zuDGMwE72sLNRILe8Bv/cchKSxLmFiIgAFjhkIK9uPYUxy37H4culoqOYNQelFT6a3B9Wchm2/5GP71NyREciIjIKLHCo3f2YmosfU/NQXFkHayv+X8zQwvxd8NzfugMAFv10GhklVYITERGJx08fale55TV4ZespAMC8kSEYEOAqOJFlePKurogMdkN1vRbPbjqOBq5XRUQWjgUOtRudTsIL355ARW0jwvxdMO/uENGRLIZCLsOHk8LgpLLCiRw1Pt93WXQkIiKh2POT2s2q/elIulwKW2sFPpwUBmvO09KhfF1s8fZDfbH3fDEeHRwoOg4RkVAd8gm0YsUKBAUFQaVSITIyEsnJyS0eO2LECMhksmu2sWPH6o+ZPn36NV8fM2ZMR9wKtSCtqBLv/3YeALDw/t4IdrcXnMgy3dfPF+9PDOVwcSKyeAZvwdm8eTNiY2OxcuVKREZGYtmyZYiJicH58+fh6el5zfE//PAD6uv/Gl5cWlqK0NBQTJw4sdlxY8aMwZo1a/SvlUql4W6CbsrVzhpj7vCGuqYBkwf6i45DaJpF+lxBBXr5OImOQkTU4Qxe4HzwwQeYNWsWZsyYAQBYuXIltm/fjtWrV+Pll1++5ng3N7dmrzdt2gQ7O7trChylUglvb2/DBac26eSgxPJH+qO2QculGIxATb0Wczak4EBaCX6aN4xFDhFZHIM+oqqvr0dKSgqio6P/+oZyOaKjo5GUlNSqa6xatQqTJ0+GvX3zRx579uyBp6cnevTogTlz5qC0tOX5Vurq6qDRaJpt1D7+72rWXPzROKis5bBWyNGglfDi9yc4qoqILI5BC5ySkhJotVp4eXk12+/l5YWCgoKbnp+cnIxTp07hiSeeaLZ/zJgxWL9+PRITE/Huu+9i7969uOeee6DVaq97nSVLlsDZ2Vm/+fvzEUp7kCQJs79Kwf/76iiKNLWi49D/kMlkeGt8HzjbWuNUroajqojI4hj1MJdVq1ahb9++GDRoULP9kydPxgMPPIC+ffti/Pjx2LZtG44cOYI9e/Zc9zpxcXFQq9X6LTs7uwPSm78fjuVi34Vi7D5fjIq6RtFx6P/wdFJh0f29AQAf7byIS8WVghMREXUcgxY47u7uUCgUKCwsbLa/sLDwpv1nqqqqsGnTJsycOfOm36dLly5wd3dHWlradb+uVCrh5OTUbKPbU1RRize2nQEAzI/uhq4eDoIT0fU82L8zRvTwQL1Wh1e3nuJaVURkMQxa4NjY2CA8PByJiYn6fTqdDomJiYiKirrhud999x3q6urw6KOP3vT75OTkoLS0FD4+PredmVrnzW1noa5pwB2+Tpg1vIvoONQCmUyGNx7oA6WVHAcvleLH1DzRkYiIOoTBH1HFxsbiiy++wLp163D27FnMmTMHVVVV+lFVU6dORVxc3DXnrVq1CuPHj0enTp2a7a+srMSLL76IQ4cOISMjA4mJiRg3bhxCQkIQExNj6NshAAfTSvDTiTzIZMA7D/XjhH5GLqCTHZ4Z1Q1dPOzh46wSHYeIqEMYfJj4pEmTUFxcjIULF6KgoABhYWGIj4/XdzzOysqCXN78A/L8+fPYv38/fvvtt2uup1Ao8Mcff2DdunUoLy+Hr68vRo8ejcWLF3MunA5Q36jDqz82rTX1aGQg+vo5C05ErTFreBc8MTwYSiuOciMiyyCTLPChvEajgbOzM9RqNfvjtNHl4ko8tioZdY1aJMaOgLMdZ8w1RZIkcb4iIjI5bfn85lpU1CZdPBywM/YuXCquZHFjghq0Oqw5kI6EM4X4ZtZgWPHxIhGZKf52ozaztVGgT2c+mjJFmpoGrNh9CUcyrmBdUqboOEREBsMCh1rl94vF2HA4EzqdxT3RNCudHJR4aUxPAMCynRdQUlknOBERkWGwwKGbqmvU4pWtp/CvLaew+kC66Dh0myYN9Eefzk6oqG3Ev6+uAE9EZG5Y4NBNrTmQgczSang6KjF5UIDoOHSbFHIZFt1/BwBg05FsnMpVC05ERNT+WODQDRVX1OGTXU0zRC8Y0xMOSvZLNwcDg9xwf6gvJAl4/efTnOGYiMwOCxy6oQ8SzqOyrhH9/JzxUP/OouNQO4q7pydU1nIczyrHmXyN6DhERO2Kf45Ti07nqbHpSNPCpAvv6w25nPOmmBNfF1u89/dQ9PZxQogn1xIjIvPCAoda9Nb2s5Ak4L5+PogIchMdhwzggVBf0RGIiAyCj6ioRQvG9MSQrp3w8j09RUehDnC+oAIF6lrRMYiI2gULHGpRmL8LNs4aDD9XO9FRyMC+/P0y7vloH97fwWHjRGQeWODQNWobtKIjUAeLCHKDTgJ+OJ6DM3nscExEpo8FDjVTXl2PO9/bjSW/nGWhY0HC/F1wXz8fSBKw5NezouMQEd02FjjUzH/2XEJRRR32XiiGNRditCgLYnrCWiHD7xdLsO9Cseg4RES3hZ9gpJdbXoO1BzMAAC+N6QkFh4VblIBOdnhscBAAYMmv56DlumNEZMJY4JDev387j/pGHQZ3ccOIHh6i45AAT98dAkeVFc7ma7DleK7oOEREt4wFDgFAsw+0uHt6QSZj640lcrW3wdyRIXCxs+byDURk0jjRHwEA3o0/B0kCxvbzQai/i+g4JND0IUF4ZGAAnO2sRUchIrplLHAIOVeqcehyKazkMrw4uofoOCSYyloBlbVCdAwiotvCAofg52qHPS+MxOH0UgS524uOQ0ZCkiQknClEUUUdHh0cKDoOEVGbsMAhAIC3swrjwrhaOP3l4KVSzP4qBXY2CsTc4Q0PR6XoSERErcZOxhZMq5PwR0656BhkpIZ07YRQfxdU12vxnz1pouMQEbUJCxwL9vOJPDzwyQE8tzlVdBQyQjKZDAtimvpkbTiUhdzyGsGJiIhajwWOhWrQ6rBs5wUAQIing+A0ZKyGhrhjSNdOqNfqsHznRdFxiIhajQWOhfpvSg4ySqvRyd4G04cEiY5DRuyFq6043x/LwaXiSsFpiIhahwWOBapr1GJ5YtNf43NGdIW9kn3NqWUDAlwR3csTWp2EDxMuiI5DRNQq/GSzQN8czkKeuhbeTioO/6VWeX50D+SW1+LB/hxpR0SmgQWOhamub8Qnuy8BAJ4eFcIJ3ahVevk44ZdnhnEJDyIyGXxEZWEySqpho5DB380WE8P9RcchE8LihohMCVtwLExvXyfsemEEcq5Uw8aK9S21TVVdI9YnZSKjpArv/r2f6DhERC3iJ5wFUlkrEOLpKDoGmaB8dQ3e23EOm49m41SuWnQcIqIWdUiBs2LFCgQFBUGlUiEyMhLJycktHrt27VrIZLJmm0qlanaMJElYuHAhfHx8YGtri+joaFy8yDk6bqS6vhFbj+eiUasTHYVMWIinI+7v5wsA+CiRP3NEZLwMXuBs3rwZsbGxWLRoEY4dO4bQ0FDExMSgqKioxXOcnJyQn5+v3zIzM5t9/b333sPy5cuxcuVKHD58GPb29oiJiUFtba2hb8dkfX0oE/M3p+LxdUdFRyET98yobpDJgIQzhWzFISKjZfAC54MPPsCsWbMwY8YM9O7dGytXroSdnR1Wr17d4jkymQze3t76zcvLS/81SZKwbNkyvPLKKxg3bhz69euH9evXIy8vD1u3bjX07ZikmnotPt93GQBwX18fwWnI1IV4OuCB0KZWnGWc3ZiIjJRBC5z6+nqkpKQgOjr6r28olyM6OhpJSUktnldZWYnAwED4+/tj3LhxOH36tP5r6enpKCgoaHZNZ2dnREZGtnjNuro6aDSaZpsl2XA4EyWV9fB3s8WDAziPCd2+p+/uBrkM2HmWrThEZJwMWuCUlJRAq9U2a4EBAC8vLxQUFFz3nB49emD16tX48ccf8fXXX0On02HIkCHIyckBAP15bbnmkiVL4OzsrN/8/S1neHRNvRYr9za13swbGQJrBfuV0+1jKw4RGTujGyYeFRWFqKgo/eshQ4agV69e+Oyzz7B48eJbumZcXBxiY2P1rzUajcUUOU2tN3Xwc7XFQwP8RMchM/L0qG6QADw1IkR0FCKiaxi0wHF3d4dCoUBhYWGz/YWFhfD29m7VNaytrdG/f3+kpaUBgP68wsJC+Pj81Z+ksLAQYWFh172GUqmEUqm8hTswbbUNWny2j603ZBhdPRzw0eT+omMQEV2XQT/xbGxsEB4ejsTERP0+nU6HxMTEZq00N6LVanHy5El9MRMcHAxvb+9m19RoNDh8+HCrr2kpSirrENzJHp1d2HpDhidJkugIRER6Bn9EFRsbi2nTpiEiIgKDBg3CsmXLUFVVhRkzZgAApk6dis6dO2PJkiUAgDfeeAODBw9GSEgIysvL8f777yMzMxNPPPEEgKYRVvPnz8ebb76Jbt26ITg4GK+++ip8fX0xfvx4Q9+OSfFztcO3T0ahtLKOsxaTwWSXVeOjxIuwsZLj7Qf7io5DRASgAwqcSZMmobi4GAsXLkRBQQHCwsIQHx+v7ySclZUFufyvD98rV65g1qxZKCgogKurK8LDw3Hw4EH07t1bf8yCBQtQVVWF2bNno7y8HMOGDUN8fPw1EwJSk04Olvd4jjpOcWUdvk/JgZVchrkjQ9DZxVZ0JCIiyCQLbFfWaDRwdnaGWq2Gk5OT6DjtTqeTsPpAOh4a4Ac3exvRccgC/OOLQzh4qRTTogLx+rg+ouMQkZlqy+c3n1uYod/OFODN7Wdx70e/c2kG6hDzRjaNpNp0JBvFFXWC0xARscAxO5IkYcXuSwCAhyP8YMWRU9QBorp2Qv8AF9Q16vDl/sui4xARscAxN79fLMHJXDVsrRWYPjRYdByyEDKZTN+K83VSJsqr6wUnIiJLxwLHzKzY3TRf0D8iA9j/hjrU3T090cvHCVX1WqxPyrz5CUREBmR0MxnTrTuaUYbD6WWwVsgwa3gX0XHIwshkMsT+rTvO5GkwLSpIdBwisnAscMzIf/Y09b35e7gfvJ05ZJ463t96e+Fvvb1ufiARkYHxEZWZ0OokeDkpobSS4//d2VV0HCJIkgSdzuJmoSAiI8F5cMxsHhx1TQOcba1FxyALd/BSCf792wWMD/PFY3xcRUTthPPgWDAWN2QM0ooqkZJ5BV/8ns65mIhICBY4ZuCb5CycydOIjkGkNzHcH6521sgqq0b86QLRcYjIArHAMXEF6los/PEU7l3+O9KKKkTHIQIA2NooMG1IEADgs72XudI4EXU4Fjgmbs3BdDRoJQwKckOIp6PoOER6U6OCoLKW42SuGkmXS0XHISILwwLHhFXUNmDjoSwAwOw7Oe8NGRc3exs8HOEPoKkVh4ioI7HAMWGbkrNRUdeIrh72uLunp+g4RNd4YlgXyGXA3gvFOFfAfmJE1HE40Z+JatDqsPpAOoCm1hu5XCY4EdG1AjrZYd7IEHTzckSIh4PoOERkQVjgmKifT+QhX10LD0clxvfvLDoOUYtiR/cQHYGILBAfUZkoSQI8HJWYPiQISiuF6DhErcLRVETUUdiCY6ImhPvhvlAf6DiHGpmABq0Oaw6kY/ORbPwwZyic7TghJREZFltwTJjSSgFbG7bekPGzksvww7FcXCquwteHM0XHISILwALHxJwvqMAvJ/Oh5SKGZEJkMhn+311NUxmsOZCB2gat4EREZO5Y4JiYT3an4akNx/Dm9jOioxC1yX39fOHrrEJJZR22HM8VHYeIzBwLHBOSXVaNX07mAwD+Hu4nOA1R21gr5Jg5vKkV54t9l9kKSUQGxQLHhKw+kA6tTsKwEHfc4essOg5Rm00e6A8nlRUul1Qh4Uyh6DhEZMZY4JgIdXUDNh/JBsBlGch02Sut8OjgQADA6v3pgtMQkTnjMHET8fXhTFTXa9HLxwnDu7mLjkN0y6YNCUJeeQ0eHxYsOgoRmTEWOCagrlGLtQczAACz7wyGTMZlGch0eTmpsGxyf9ExiMjMscAxAcUVdejsYgu5DBjb11d0HCIiIqPHAscE+LnaYevcoSiuqIONFbtNkXnIKKnCZ/suw8NRidi/dRcdh4jMDD8tTYiHo1J0BKJ2c6m4Et8kZ2HNgXRU1jWKjkNEZoYFjpH79WQ+1NUNomMQtbuRPTzRxd0eFbWN+O5otug4RGRmWOAYsYySKjy18RiGvJOIK1X1ouMQtSu5XKYfSfXnHE9ERO2lQwqcFStWICgoCCqVCpGRkUhOTm7x2C+++ALDhw+Hq6srXF1dER0dfc3x06dPh0wma7aNGTPG0LfR4dYcSIckAYOC3eBqbyM6DlG7mzDADy521sguq0HCmQLRcYjIjBi8wNm8eTNiY2OxaNEiHDt2DKGhoYiJiUFRUdF1j9+zZw8eeeQR7N69G0lJSfD398fo0aORm9t87ZoxY8YgPz9fv33zzTeGvpUOpa5pwHcpOQCAmcM4sR+ZJ1sbBR6NbJr478vfOfEfEbUfgxc4H3zwAWbNmoUZM2agd+/eWLlyJezs7LB69errHr9hwwY89dRTCAsLQ8+ePfHll19Cp9MhMTGx2XFKpRLe3t76zdXV1dC30qE2JWehul6Lnt6OGBrSSXQcIoOZGhUIa4UMRzOv4HjWFdFxiMhMGLTAqa+vR0pKCqKjo//6hnI5oqOjkZSU1KprVFdXo6GhAW5ubs3279mzB56enujRowfmzJmD0tLSFq9RV1cHjUbTbDNmjVod1l2d2O/xoZzYj8ybp5MK06KC8MzdIfB3sxMdh4jMhEHnwSkpKYFWq4WXl1ez/V5eXjh37lyrrvHSSy/B19e3WZE0ZswYPPTQQwgODsalS5fwz3/+E/fccw+SkpKgUCiuucaSJUvw+uuv397NdKBfTxUgT10LdwcbPBDGif3I/L1yX2/REYjIzBj1RH/vvPMONm3ahD179kClUun3T548Wf/fffv2Rb9+/dC1a1fs2bMHo0aNuuY6cXFxiI2N1b/WaDTw9/c3bPjbkFFSBSu5DFMiA6GyvrZgIyIiohszaIHj7u4OhUKBwsLCZvsLCwvh7e19w3OXLl2Kd955Bzt37kS/fv1ueGyXLl3g7u6OtLS06xY4SqUSSqXpTJL39KhumBjhD5U1R/GT5ZAkCXvOF2PD4Sx8OCkUjipr0ZGIyIQZ9BPUxsYG4eHhzToI/9lhOCoqqsXz3nvvPSxevBjx8fGIiIi46ffJyclBaWkpfHx82iW3MfB2VsHFjkPDyXJIErB4+xnsPFuI76+OICQiulUGbyKIjY3FF198gXXr1uHs2bOYM2cOqqqqMGPGDADA1KlTERcXpz/+3XffxauvvorVq1cjKCgIBQUFKCgoQGVlJQCgsrISL774Ig4dOoSMjAwkJiZi3LhxCAkJQUxMjKFvx6CKNLVIK6oQHYNICLlchhlDggAA6w5mQMeJ/4joNhi8wJk0aRKWLl2KhQsXIiwsDKmpqYiPj9d3PM7KykJ+fr7++E8//RT19fX4+9//Dh8fH/22dOlSAIBCocAff/yBBx54AN27d8fMmTMRHh6O33//3aQeQ13PF79fRvQH+7B0x3nRUYiEeGiAHxxVVsgorcbu89efK4uIqDVkkiRZ3J9JGo0Gzs7OUKvVcHJyEh0HAFBZ14iotxNRUdeINdMHYmRPT9GRiIR4a/sZfPF7OoaFuOPrJyJFxyEiI9KWz2/2YjUS3x3NRkVdI7p42OOu7h6i4xAJMzUqCHIZsD+tBBcK+ciWiG4NCxwjoNVJWHMgAwAwY2gw5HJO7EeWy9/NDqN7N42y/PPngoiorYx6HhxLsfNsIbLKquFsa40JAzqLjkMk3IyhQcgqq8bgLm43P5iI6DpY4BiB1fubFhn8R2QA7Gz4T0I0KNgN258ZxmVKiOiW8dNUsLKqelwsqoRCLsPUqEDRcYiMAgsbIrpdLHAEc7O3wcGX78axrCvwcbYVHYfIqFTWNeK7o9kIdrfHiB4cWUhErccCxwiorBUY0tVddAwio/Pl75exbOdFhAe6ssAhojbhKCqBssuqOVsr0Q38Y1AArBUypGRewR855aLjEJEJYYEjSKNWh4c/S8KoD/YirahSdBwio+TppMLYvk1rzHHIOBG1BQscQX47U4h8dS00NQ3wc2XfG6KWzBgaDADY9kceijS1gtMQkalggSPI2qt/jf4jMgAqa4XYMERGLNTfBQMCXNCglfD14SzRcYjIRLDAEeBUrhrJGWWwksswJZJDw4lu5vFhTa04Gw9noq5RKzgNEZkCFjgCrDuYAQC4p68PvJ1VYsMQmYCYO7zh52qLiEA3qGsaRMchIhPAYeIdrLSyDj+eyAMATB8SJDYMkYmwVsixM/YuPs4lolZjC04H++VUAeobdejn54wBAS6i4xCZDBY3RNQWbMHpYI9GBqCbpwMkidPRE92KzNIqHL5chocH+ouOQkRGjAVOB5PJZBjcpZPoGEQmKa+8BiOX7gEADAnpBD9XO7GBiMho8RFVB6qp5+gPotvh62KLqK6doJOArw5lio5DREaMBU4HOZmjxqC3d2LJr2chSVyegehWzRjSNGR8U3I2/2ggohaxwOkgaw9moKK2EQXqWva9IboNI3t6IsDNDuqaBmxNzRUdh4iMFAucDlBSWYefOTScqF0o5DJMjWqaIHPNgXS2iBLRdbHA6QDfHM5CvVaHUH8X9A9wFR2HyORNjPCHnY0CFworkXSpVHQcIjJCLHAMrEGr03eGnMHWG6J24WxrjQkD/OCkskK+mgtwEtG1OEzcwH49VYCiijp4OCpxb18f0XGIzMZzf+uOuHt7ws6Gv8aI6Fr8zWBg66+uOzUlMgA2VmwwI2ovbvY2oiMQkRHjJ66BfTgpDLOGB+MfkQGioxCZJUmScDCtBFV1jaKjEJERYYFjYP5udvjX2N7wdOSq4USGMPurFPzjy8PYcpxDxonoLyxwDIRDV4k6RtTVpU/WHszgzx0R6bHAMZBPdqVh1vqjOJFdLjoKkVmbGOEHexsF0ooqsT+tRHQcIjISLHAMoL5Rh/WHMpFwphCZZdWi4xCZNUeVNSZGNK0svvZAhtgwRGQ0WOAYwK+n8lFcUQcvJyXu6eMtOg6R2ftzZuNd54uQUVIlOA0RGYMOKXBWrFiBoKAgqFQqREZGIjk5+YbHf/fdd+jZsydUKhX69u2LX375pdnXJUnCwoUL4ePjA1tbW0RHR+PixYuGvIU2WXP1r8hHIwNhrWANSWRoXTwcMKKHByQJWJ/EVcaJqAMKnM2bNyM2NhaLFi3CsWPHEBoaipiYGBQVFV33+IMHD+KRRx7BzJkzcfz4cYwfPx7jx4/HqVOn9Me89957WL58OVauXInDhw/D3t4eMTExqK0VP6Pp8awrSM0uh41Cjkc4NJyow/y5zltK1hV2NiYiyCQD/yaIjIzEwIED8cknnwAAdDod/P398fTTT+Pll1++5vhJkyahqqoK27Zt0+8bPHgwwsLCsHLlSkiSBF9fXzz//PN44YUXAABqtRpeXl5Yu3YtJk+efNNMGo0Gzs7OUKvVcHJyaqc7bTJ/03FsTc3DhAF++PfDoe16bSJqmU4n4VB6KQYHd4JcLhMdh4gMoC2f3wZtwamvr0dKSgqio6P/+oZyOaKjo5GUlHTdc5KSkpodDwAxMTH649PT01FQUNDsGGdnZ0RGRrZ4zbq6Omg0mmabIRRparH9ZD4ArhpO1NHkchmGdHVncUNEAAxc4JSUlECr1cLLy6vZfi8vLxQUFFz3nIKCghse/+f/tuWaS5YsgbOzs37z9/e/pfu5GQeVFRbe1xsPDeiMvn7OBvkeRHRztQ1a5JXXiI5BRAJZRA/YuLg4qNVq/ZadnW2Q72NnY4XHooLwwcNhBrk+Ed1c4tlCDF6SiH9tOSk6CpHFadDqjKYPnEELHHd3dygUChQWFjbbX1hYCG/v6w+f9vb2vuHxf/5vW66pVCrh5OTUbCMi89TVwwHqmgbsPl+MdA4ZJ+pQaw9kYMyy3xF/6vpPVDqSQQscGxsbhIeHIzExUb9Pp9MhMTERUVFR1z0nKiqq2fEAkJCQoD8+ODgY3t7ezY7RaDQ4fPhwi9ckIssR5G6Pu3t4AgDWHcwQG4bIgmh1EtYlZeB8YQXUNfWi4xj+EVVsbCy++OILrFu3DmfPnsWcOXNQVVWFGTNmAACmTp2KuLg4/fHPPvss4uPj8e9//xvnzp3Da6+9hqNHj2LevHkAAJlMhvnz5+PNN9/ETz/9hJMnT2Lq1Knw9fXF+PHjDX07RGQCpg8NAgB8dzQbFbUNYsMQWYjEs4XIuVIDFztrjAvrLDoOrAz9DSZNmoTi4mIsXLgQBQUFCAsLQ3x8vL6TcFZWFuTyv+qsIUOGYOPGjXjllVfwz3/+E926dcPWrVvRp08f/TELFixAVVUVZs+ejfLycgwbNgzx8fFQqbhiNxEBw0LcEeLpgLSiSnyfkoMZQ4NFRyIye+uSMgAAkwcGQGWtEBsGHTAPjjEy5Dw4RGQcvjqUiVe3nkJQJzvsen4Eh48TGdCFwgqM/nAf5DLg95fuRmcXW4N8H6OZB4eISJQJAzrDUWWFjNJqpOaUi45DZNbWXu3vNrq3t8GKm7Yy+CMqIiIR7GyssHRiKEI8HdDVw0F0HCKzpa5pwJZjuQD+6v9mDFjgEJHZirnj+lNHEFH7cVRaYeVj4Ug8W4jIYDfRcfRY4BCRRaiqa4S9kr/yiNqbXC7DXd09cFd3D9FRmmEfHCIyaxW1DZi78RiiliRCXcMh40SWggUOEZk1B6UVLhZWQFPbiO+OGmaZFiJLNXfjMbwbfw4llXWio1yDBQ4RmTWZTIbpQ5rmwVmflAmtzuJmxiAyiAuFFdj+Rz4+23sJtQ1a0XGuwQKHiMze+P6+cLa1RlZZNXafKxIdh8gsrPufoeF+rnZiw1wHCxwiMnt2NlaYPNAfwF/zdRDRrVNXN+CHq0PDpw0JEhumBSxwiMgiPBYVCLkM2J9WgouFFaLjEJm0b49mo6ZBi57ejhjcxXiGhv8vFjhEZBH8XO0wunfTvDhfHcoUnIbIdGl1EtYfygDQ1HojkxnnMiicFIKILMbsu7ogIsgVEyP8RUchMlm7zhUhu6wGzrbWGG8Eq4a3hAUOEVmMAQGuGBDgKjoGkUnr4eWIaVGBcLNXwtZG/KrhLWGBQ0QWSZKahosba/M6kbEK6GSH18f1ER3jptgHh4gsTvypfIxbcQC/nSkUHYWIDIQFDhFZnBM5avyRo8baAxmioxCZDHV1A+ZvOo6UzDJ9C6gxY4FDRBbn0cGBUMhlSLpcinMFGtFxiEzCpiNZ2Jqah39tOSU6SquwwCEii9PZxRYxd3gB+Gs2ViJqWaNWp/9ZeXxYsEn0XWOBQ0QWacbQpvWpthzPxZWqesFpiIzbb2cKkaeuRSd7GzwQ6is6TquwwCEiixQR6Io7fJ1Q26DDpiNcZZzoRlbvTwcATIkMgMraeIeG/y8WOERkkZpWGQ8CAHyVlIFGrU5sICIj9UdOOY5mXoG1QoZHBweKjtNqnAeHiCzW/aG+SDhTiAnhfibRp4BIhDVXRxve188Xnk4qsWHagAUOEVkslbUCn0+NEB2DyKj1D3DB0cwyzBgaJDpKm8gkUxjM3s40Gg2cnZ2hVqvh5OQkOg4REZFR0+kkyOXiWznb8vnNFhwisnillXX4+lAWahq0ePmenqLjEBkdYyhu2oqdjInI4mWUVuPDnRew+kA6yjhknAgAsOtcIbYcz0F9o2l2wGeBQ0QWb0CAC/r5OaO+UYdvkrNExyESTpIkvL/jAp7bfALrkzJEx7klLHCIyOI1HzKeiQYOGScLd+hyGc7ma6CyluPv4X6i49wSFjhERADG9vOBu4MNCjS12HG6QHQcIqHWHGia2O+hAX5wsbMRnObWsMAhIgKgtFLgH5FNk5hxlXGyZFml1Ug4WwgAmHG1ZdMUscAhIrrq0cgAWCtkOJp5BSdz1KLjEAmxLikDkgQM7+aObl6OouPcMoMWOGVlZZgyZQqcnJzg4uKCmTNnorKy8obHP/300+jRowdsbW0REBCAZ555Bmp18180Mpnsmm3Tpk2GvBUisgCeTipMGOCHSRH+cLLlLBpkeSrrGvHt1bXZHh8WLDjN7THoT/CUKVOQn5+PhIQENDQ0YMaMGZg9ezY2btx43ePz8vKQl5eHpUuXonfv3sjMzMSTTz6JvLw8fP/9982OXbNmDcaMGaN/7eLiYshbISILseShvly2gSxWaWUd+nR2RmFFLe7q5iE6zm0x2EzGZ8+eRe/evXHkyBFERDRNhR4fH497770XOTk58PVt3XLr3333HR599FFUVVXByqqpHpPJZNiyZQvGjx9/S9k4kzEREVHLKmob4KiyFh3jGm35/DbYI6qkpCS4uLjoixsAiI6Ohlwux+HDh1t9nT9v4s/i5k9z586Fu7s7Bg0ahNWrV+NGdVpdXR00Gk2zjYjoRk7nqfGvLSdR26AVHYWowxljcdNWBitwCgoK4Onp2WyflZUV3NzcUFDQuiGYJSUlWLx4MWbPnt1s/xtvvIFvv/0WCQkJmDBhAp566il8/PHHLV5nyZIlcHZ21m/+/v5tvyEishhanYTZ61Ow4XAWth7PFR2HqEN8ezQbJZV1omO0mzYXOC+//PJ1O/n+73bu3LnbDqbRaDB27Fj07t0br732WrOvvfrqqxg6dCj69++Pl156CQsWLMD777/f4rXi4uKgVqv1W3Z29m3nIyLzpZDL9Csnf7k//YYtxETm4EyeBgu+/wN3vrcbmtoG0XHaRZs7GT///POYPn36DY/p0qULvL29UVRU1Gx/Y2MjysrK4O3tfcPzKyoqMGbMGDg6OmLLli2wtr5xU1lkZCQWL16Muro6KJXKa76uVCqvu5+IqCUPD/THsp0XkVZUib0XijGih+fNTyIyUV/uvwwAGNXLC05m8HgKuIUCx8PDAx4eN+9ZHRUVhfLycqSkpCA8PBwAsGvXLuh0OkRGRrZ4nkajQUxMDJRKJX766SeoVKqbfq/U1FS4urqyiCGiduOkssakgf5YtT8dq/ans8Ahs1WoqcXPJ/IAAE+Y+NDw/2WwPji9evXCmDFjMGvWLCQnJ+PAgQOYN28eJk+erB9BlZubi549eyI5ORlAU3EzevRoVFVVYdWqVdBoNCgoKEBBQQG02qaOfj///DO+/PJLnDp1Cmlpafj000/x9ttv4+mnnzbUrRCRhZo+JAhyGfD7xRKcK+DgBDJP6w5moEErYVCQG0L9XUTHaTcGnQdnw4YNmDdvHkaNGgW5XI4JEyZg+fLl+q83NDTg/PnzqK6uBgAcO3ZMP8IqJCSk2bXS09MRFBQEa2trrFixAs899xwkSUJISAg++OADzJo1y5C3QkQWyN/NDvf08cH2k/lY9Xs63p8YKjoSUbuqrm/EhsNZAICZw82n9QYwcIHj5ubW4qR+ABAUFNSs896IESNu2plvzJgxzSb4IyIypJnDg3EkowzdTXjKeqKWfJ+SA3VNAwI72SG6l5foOO2Kc5ETEd3AgABXHHj5blgruHQfmZ8rVQ2wsZJj5rBgKOTmNYM3CxwioptgcUPm6tnobpgyOAD2NuZXDpjfHRERGYBWJ+G30wWwVsgR3du8mvLJsrk7mOcIZBY4REStsOlIFv615RS6etjj7p6ekJtZcz5ZlrSiStQ2aNGns7PoKAbDdlciolZ4INQXjkorXCquwt4LxaLjEN2WZTsv4L6P92PF7jTRUQyGBQ4RUSs4qqwxeVDTOnZf/H5ZcBqiW5dzpRq/nmpaE3KkGU9gyQKHiKiVpg9tGmly8FIpTuWqRcchuiVrD2RAq5MwNKQTevs6iY5jMCxwiIhaqbOLLe7r5wMA+GwfW3HI9FTUNmDTkaYFp58Y3kVwGsNigUNE1Aaz72z6UPjlZD6yy6oFpyFqm03J2aisa0SIpwPu6nbzdSVNGUdRERG1wR2+zhjezR0VtY1Q1zTAX3Qgolaqb9Rh1f50AMCs4cFmPxKQBQ4RURt9+mg47G0UkMnM+wOCzEtmaRVkMsDTUYnx/TuLjmNwLHCIiNrIQclfnWR6unk5Yu+LI5FRWgWllUJ0HINjHxwiolukrm7AZ3svoaZeKzoKUavYWMktZuFY/hlCRHQLJEnCpM+TcK6gAnZKKzw2OFB0JKIW7TlfhGEh7rCyoHXVLOdOiYjakUwmw+SBTV2Mv/z9MrQ6SXAious7mlGG6WuOYPSyfWjQ6kTH6TAscIiIbtHDA/3hYmeNzNJq7DhdIDoO0XX9OWfTwEA3WLMFh4iIbsbOxgpTrz6a+mzvJUgSW3HIuKQVVSDhTCFkMmD2XeY9sd//xQKHiOg2TB0SBKWVHCdy1Dh0uUx0HKJmPr/aevO3Xl7o6uEgOE3HYoFDRHQb3B2UmBjhBwD4bN8lwWmI/lKgrsWW47kAgCdHdBWcpuOxwCEiuk1PDOsCGys53Oxs0GhBnTjJuK05kI4GrYRBQW4YEOAqOk6H4zBxIqLbFORuj+R/joKLnY3oKEQAmqYxuFhUCQB4coRl9b35EwscIqJ2wOKGjIlMJsPq6QNxIrscfTs7i44jBB9RERG1owuFFfjuaLboGEQAgFB/F7NfVLMlbMEhImonFworMPrDfbBRyHFndw94OalERyILlJpdjgA3O7jZW3arIltwiIjaSTdPB0QEuqJeq8MXV4fnEnWkBq0O8zYew9B3duFIhmVPW8ACh4ionchkMsy9OwQAsOFwFsqq6gUnIkvzY2oecq7UwF6psNi+N39igUNE1I5GdPdAn85OqGnQYs2BdNFxyIJodRL+szsNADBreBeorBWCE4nFAoeIqB3JZDLMHdHUirP2YAY0tQ2CE5Gl+OVkPi6XVMHFzhpTuLo9CxwiovYWc4c3QjwdUFHbiK+SMkXHIQug00n4ZFdT683jQ4PhoOQYIhY4RETtTC6XYe7IruhkbwMnFT9oyPB2ni3E+cIKOCqtMG1IkOg4RoE/eUREBnB/P1+MucMHtjaW3Q+COkZGaRWsFTI8FhUIZ1tr0XGMgkFbcMrKyjBlyhQ4OTnBxcUFM2fORGVl5Q3PGTFiBGQyWbPtySefbHZMVlYWxo4dCzs7O3h6euLFF19EY2OjIW+FiKhNrBRyFjfUYWbf2RX7FozE7Dstc1mG6zFoC86UKVOQn5+PhIQENDQ0YMaMGZg9ezY2btx4w/NmzZqFN954Q//azs5O/99arRZjx46Ft7c3Dh48iPz8fEydOhXW1tZ4++23DXYvRES3QqeTkHC2EAqZDNG9vUTHITPm42wrOoJRMViBc/bsWcTHx+PIkSOIiIgAAHz88ce49957sXTpUvj6+rZ4rp2dHby9va/7td9++w1nzpzBzp074eXlhbCwMCxevBgvvfQSXnvtNdjYWPbMjURkXL5LycZL/z2JwE52GNHDA1YKdn2k9nM2XwOdJOEOX8ue8+Z6DPaTlpSUBBcXF31xAwDR0dGQy+U4fPjwDc/dsGED3N3d0adPH8TFxaG6urrZdfv27Qsvr7/+EoqJiYFGo8Hp06eve726ujpoNJpmGxFRR7g/1Bdu9jbILK3Gtj/yRcchM/PW9rMYu3w/1idliI5idAxW4BQUFMDT07PZPisrK7i5uaGgoKDF8/7xj3/g66+/xu7duxEXF4evvvoKjz76aLPr/m9xA0D/uqXrLlmyBM7OzvrN39//Vm+LiKhN7GysMHNYMADg410XodVJghORuTiWdQX700pgJZdhZA/Pm59gYdpc4Lz88svXdAL+v9u5c+duOdDs2bMRExODvn37YsqUKVi/fj22bNmCS5cu3fI14+LioFar9Vt2Nlf6JaKOMzUqEC521rhUXIVtf+SJjkNmYsXVeW8e7N8Z/m52Nzna8rS5D87zzz+P6dOn3/CYLl26wNvbG0VFRc32NzY2oqysrMX+NdcTGRkJAEhLS0PXrl3h7e2N5OTkZscUFhYCQIvXVSqVUCqVrf6eRETtyVFljVnDu+D9HefxUeJF3NfPFwq5THQsMmEnc9RIPFcEuQyYM6Kr6DhGqc0FjoeHBzw8PG56XFRUFMrLy5GSkoLw8HAAwK5du6DT6fRFS2ukpqYCAHx8fPTXfeutt1BUVKR/BJaQkAAnJyf07t27jXdDRNQxpg0Jwhe/X8bl4ir8fCIP4/t3Fh2JTNiHOy8AAMaFdUYXDwfBaYyTwfrg9OrVC2PGjMGsWbOQnJyMAwcOYN68eZg8ebJ+BFVubi569uypb5G5dOkSFi9ejJSUFGRkZOCnn37C1KlTceedd6Jfv34AgNGjR6N379547LHHcOLECezYsQOvvPIK5s6dy1YaIjJaDkorzBreBX06O8HTkb+r6NYdz7qCXeeKoJDL8MyobqLjGC2DzoOzYcMGzJs3D6NGjYJcLseECROwfPly/dcbGhpw/vx5/SgpGxsb7Ny5E8uWLUNVVRX8/f0xYcIEvPLKK/pzFAoFtm3bhjlz5iAqKgr29vaYNm1as3lziIiM0ew7u+CpEV0hk/HxFN260sp6eDgqcVd3DwS724uOY7RkkiRZXJd+jUYDZ2dnqNVqODk5iY5DRETUJrUNWlTXa+Fmb1lzv7Xl85szThERdbDKukb8Z08afjnJeXHo1qisFRZX3LQVCxwiog72zeEsvBd/Hu/vOI9GrU50HDIRqdnl+OlEHudSaiUWOEREHewfkQFws7dBekkVfjiWKzoOmYh3fj2LZ745jo8SL4qOYhJY4BARdTB7pRWeujp3ybKdF1DXqBWciIzdwUslOHS5DDYKOSYN5Gz8rcECh4hIgEcHB8LHWYU8dS02HMoSHYeMmCRJWLrjPABg0kB/dHbhquGtwQKHiEgAlbUCT9/dNIfJit1pqKprFJyIjFXi2SIcyyqHylqOp+8OER3HZLDAISISZGKEHwI72aG0qh5rDqSLjkNGSKuT8P7V1psZQ4Ph6aQSnMh0GHSiPyIiapm1Qo7Yv3VHwplC3NPXR3QcMkI/ncjF+cIKOKms8OSdXHOqLVjgEBEJNC6sM8aFcV0qur4ANzuE+btg9B1ecLazFh3HpLDAISIyIpIkcSkH0gsPdMOWp4Zw7ptbwD44RERGILusGrGbU/H6z2dERyEjI5PJYKXgx3Vb8R0jIjICOVdq8MPxXHx9KBOXiytFxyHBVu1Pxwe/nYemtkF0FJPFAoeIyAhEde2Eu3t6olEn4b3486LjkEBXquqxbOcFLN+Vht3nikTHMVkscIiIjMTL9/SEXAbEny7A0Ywy0XFIkI8SL6KithG9fJxwfz9f0XFMFgscIiIj0d3LEQ9HNE3D//YvZyFJ7FhqadJLqvD1oUwAwCtje0EuZ4fzW8UCh4jIiDz3t+6wtVbgWFY54k8ViI5DHeydX8+iUSdhZA8PDA1xFx3HpLHAISIyIl5OKswaHgwA+HI/Zze2JMnpZdhxuhByGfDPe3uJjmPyOA8OEZGRmX1XV1gp5JgxNEh0FOpAS39r6lw+eVAAunk5Ck5j+tiCQ0RkZByUVnhmVDc4qjhzrSX54OFQTAz3w3PR3UVHMQsscIiIjJgkSTiVqxYdgzqAn6sd3p8YCg9HpegoZoEFDhGRkaqsa8SETw9i/IoDuMTJ/8xWUUWt6AhmiQUOEZGRclBawcXOBo06CW9u4xIO5qhQU4u7l+7F098cR2Vdo+g4ZoUFDhGREXtlbC9YK2TYfb6Ys9qaoXd/PYfKukbkXKmGnbVCdByzwgKHiMiIdfFwwIyhTcPGF287g/pGneBE1F5SMsvww/FcyGTAa/ffwUn92hkLHCIiIzfv7hC4O9jgckkV1idliI5D7UCrk7Dop9MAgIfD/RHq7yI2kBligUNEZOScVNZYENMTAPDRzosoqawTnIhu1+Yj2TiVq4GjygovjukhOo5ZYoFDRGQC/h7uh76dnRHQyQ5XqupFx6HboK5uwPs7zgEAnovuDncHDgs3BM5kTERkAuRyGVZNi0AnByUU7Kth0tJLq2BjJUd3Lwc8FhUoOo7ZYoFDRGQiPJ1UoiNQOwjzd8Gu50egQFMLawUfpBgK31kiIhNT26DFhwkX8OXvl0VHoVtkr7RCVw8H0THMGltwiIhMTMKZQnyUeBEqazli7vCGv5ud6EjUCt8eyQZkwMRwP8hkfMxoaAZtwSkrK8OUKVPg5OQEFxcXzJw5E5WVLU83npGRAZlMdt3tu+++0x93va9v2rTJkLdCRGQ07uvng8hgN9Q26PD6z6dFx6FWyFfX4PWfT2PB939gx+kC0XEsgkELnClTpuD06dNISEjAtm3bsG/fPsyePbvF4/39/ZGfn99se/311+Hg4IB77rmn2bFr1qxpdtz48eMNeStEREZDJpPhrQf7wFohw86zRfiNH5hG77WfTqOqXosBAS4Y3dtbdByLYLBHVGfPnkV8fDyOHDmCiIgIAMDHH3+Me++9F0uXLoWvr+815ygUCnh7N/+H37JlCx5++GE4ODR/Vuni4nLNsUREliLE0xGz7+yCFbsv4bWfTmNIiDsclOx1YIx+O12AHacLYSWXYclD/ThjcQcxWAtOUlISXFxc9MUNAERHR0Mul+Pw4cOtukZKSgpSU1Mxc+bMa742d+5cuLu7Y9CgQVi9ejUkSWrxOnV1ddBoNM02IiJTN29kN/i72SJPXYt3fz0nOg5dR2Vdo37G4tl3dkEPb0fBiSyHwQqcgoICeHp6NttnZWUFNzc3FBS0rjl11apV6NWrF4YMGdJs/xtvvIFvv/0WCQkJmDBhAp566il8/PHHLV5nyZIlcHZ21m/+/v5tvyEiIiNja6PAOw/1AwD8cCwHxRWc4djYLN1xHvnqWgS42eGZUd1Ex7EobS5wXn755RY7Av+5nTt3+39J1NTUYOPGjddtvXn11VcxdOhQ9O/fHy+99BIWLFiA999/v8VrxcXFQa1W67fs7OzbzkdEZAyGhrjjtft749dn74SHI2fENSbZZdX46lAmAOCtB/tAxdXCO1SbH9g+//zzmD59+g2P6dKlC7y9vVFUVNRsf2NjI8rKylrVd+b7779HdXU1pk6detNjIyMjsXjxYtTV1UGpvPYHXKlUXnc/EZE5mH51tXEyLv5udvj2/w3GgbRSDO/mITqOxWlzgePh4QEPj5v/Q0VFRaG8vBwpKSkIDw8HAOzatQs6nQ6RkZE3PX/VqlV44IEHWvW9UlNT4erqyiKGiCxe0qVSKK3lGBDgKjoKAQgPdEN4oJvoGBbJYF3ue/XqhTFjxmDWrFlYuXIlGhoaMG/ePEyePFk/gio3NxejRo3C+vXrMWjQIP25aWlp2LdvH3755Zdrrvvzzz+jsLAQgwcPhkqlQkJCAt5++2288MILhroVIiKT8GNqLp7dlIpgd3v88sxw2NrwkYgIKZlX4GxrjRBPzlQskkHnwdmwYQN69uyJUaNG4d5778WwYcPw+eef67/e0NCA8+fPo7q6utl5q1evhp+fH0aPHn3NNa2trbFixQpERUUhLCwMn332GT744AMsWrTIkLdCRGT0RvTwhJeTEuklVVj623nRcSySprYBT288hrHLf8fBtBLRcSyaTLrR+GozpdFo4OzsDLVaDScnJ9FxiIjaze5zRZix9ggAYP3jg3Bnd/b96EgLvj+Bb4/mIMDNDvHzh8POhnMTtae2fH5zsU0iIjMysqcnHhscCAB4/rsTKK3k0PGO8tvpAnx7NAcyGbB0YiiLG8FY4BARmZl/je2Fbp4OKK6ow0v//eOGE6FS+8grr8GL3/8BAHhiWDAGBbNjsWgscIiIzIzKWoHlj/SHjZUcO88WYd9F9gUxpEatDs9uOg51TQP6+TnjxZieoiMRDDiKioiIxOnl44RF9/eGnY0Cd7EfjkF9n5KDIxlX4KC0wsdXC0sSjwUOEZGZmhIZKDqCRZgY4Y8CTS2C3e0R2MledBy6igUOEZEFKKmsw4+peZg5jLMetzeFXIb50d1Fx6D/gwUOEZGZq6nXYtwnB5BbXgM7GwUeGRQgOpLJ0+okrD2YgSmRAVxjykjxQSERkZmztVHgH5FNRc2iH08jNbtcbCAz8GHCBSzedgZTVydzlJqRYoFDRGQBnhrRFaN7e6Feq8NTX6dwfpzb8MvJfHyyOw0AMCUyADKZTHAiuh4WOEREFkAmk2Hpw6Ho4m6PPHUtnv7mOBq1OtGxTM65Ag1e+O4EAGDW8GCMC+ssOBG1hAUOEZGFcFJZY+Vj4bCzUeDgpVK8G39OdCSTUl5dj9nrU1Bdr8XQkE54aQznuzFmLHCIiCxIdy9HvPf3fgCA3eeLUVXXKDiRaWjU6vD0N8eRVVYNP1dbfPLIAFgp+BFqzDiKiojIwtzXzxd1DTpE9/KCvZIfA62Rc6UGp/M0sLVW4PPHIuBqbyM6Et0EVxPnauJERKiub+TikDeRXlKFjJIqjOzpKTqKxeJq4kRE1GrrDmZg1L/3Ire8RnQUo6OubtD/d7C7PYsbE8ICh4jIgtU2aLHxcBby1bWYsSa52Qe6pdt5phDD3tuFvReKRUehW8ACh4jIgqmsFVgzYyA8HZW4UFiJqasPQ1PLIicl8wrmfXMMFbWNiD+VLzoO3QIWOEREFs7XxRbrZw6Cq501TuSoMW11MiosuMg5nnUF09cko7ZBh5E9PPDGuD6iI9EtYIFDRETo6e2Er5+IhLOtNY5nlWPGmiMWOYQ8JbMMj61KRkVtIwYFuWHFlAGw5nBwk8R/NSIiAgDc4euMDU9EwkllhaOZV/DLSct6NJOcXoapq5JRWdeIwV3csPbxgRxZZsL4L0dERHp9Ojvjq5mROHS5FBMj/EXH6VDfp2Sj6uosxV9OHQhbG64SbspY4BARUTOh/i4I9XfRv1bXNKC+UQcPR6W4UB3g7Qf7IsjdHo8PDYbKmsWNqeMjKiIialFtgxaz1h3F31cexKXiStFx2t3eC8X6RUetFHI8NSKExY2ZYIFDREQtKq2qR76mBpml1XjoPwdx8FKJ6EjtQquT8G78OUxbnYzXfj4NC5zU3+yxwCEiohZ1drHFlqeGon+AC9Q1DZi6KhnrkzJMuiDQ1DZg1vqj+HTPJQCAiy3XlTJHLHCIiOiG3B2U+GbWYNwf6otGnYSFP55G7LcnUF1vesPIT+epMf6TA9h1rghKKzmWTQrDCzE9IJPJREejdsZOxkREdFMqawWWTw5DqJ8zlvx6DluO56JRJ+HjR/qLjtYqkiTh60OZWLz9LOobdfBxVuGzx8LRz89FdDQyEBY4RETUKjKZDE8M74I+nZ3x8n//wLOjuomO1GqlVfV4f8d51DfqMKqnJ5ZODIWrPR9NmTOZZMoPUm9RW5ZbJyKia2l1EhTyvx7rrN6fjoggV6NqEdHqJMhl0D9++jE1F8UVdZg5LJiPpExUWz6/2YJDRERt9r/FTWp2ORZvPwMAeDjcH8/HdIeno0pUNABNsxK/se005o3shjF9vAEA48I6C81EHYudjImI6Lb4udrigVBfSBKw+Wg2Rr6/B+/vOIcrVfUdnuVUrhoz1iTj4c+ScCpXg2U7L5j0iC+6dQYrcN566y0MGTIEdnZ2cHFxadU5kiRh4cKF8PHxga2tLaKjo3Hx4sVmx5SVlWHKlClwcnKCi4sLZs6cicpK85t8iojIVLg7KPHR5P7475wohPq7oKpeixW7L2HYu7vwxs9noK4x7MrkOp2EfReK8diqw7jv4/3Yfb4YCrkMjwwKwFczI/k4ykIZrMCpr6/HxIkTMWfOnFaf895772H58uVYuXIlDh8+DHt7e8TExKC2tlZ/zJQpU3D69GkkJCRg27Zt2LdvH2bPnm2IWyAiojYID3TDljlD8Nlj4bjD1wlV9Vr8mJoLpdVfHzV/zhrcnv619RSmrk7G7xdLIJcBD4T6IuG5O7Hkob5mv7wEtczgnYzXrl2L+fPno7y8/IbHSZIEX19fPP/883jhhRcAAGq1Gl5eXli7di0mT56Ms2fPonfv3jhy5AgiIiIAAPHx8bj33nuRk5MDX1/fVmViJ2MiIsOSJAl7LhSjvLoeD/b3A9DU0nLX0t3wdbbFnd090D/ABX06O8NJZd2q6+Wpa5GaVY4jGWV4ZFAAeng7AgB2nSvEs9+kYkK4H2YOC4a/m51B743EMclOxunp6SgoKEB0dLR+n7OzMyIjI5GUlITJkycjKSkJLi4u+uIGAKKjoyGXy3H48GE8+OCD1712XV0d6urq9K81Go3hboSIiCCTyTCyh2ezfcezy5FdVoPsshocTi/T7/dyUsLf1Q6TBvrrVzAvUNdi6W/nUVZVj6KKWqQXV6GqXqs/x1FlhR7ePQAAd3X3RPK/orn6NzVjNAVOQUEBAMDLy6vZfi8vL/3XCgoK4OnZ/AfGysoKbm5u+mOuZ8mSJXj99dfbOTEREbVFeKAr9rwwAr9fLEbS5VL8kaNGzpUaFGrqUKipw5AQd/2xlXUN+D4lp9n5VnIZunk5YlCQKyKDO+n3K+QyFjd0jTYVOC+//DLefffdGx5z9uxZ9OzZ87ZCtbe4uDjExsbqX2s0Gvj7+wtMRERkmYLc7RHkbo/HooIAAOXV9cgsrUZWWTWC3e31x7k7KPFiTA90sreBu4MSgZ3sEORuD2sFB/9S67SpwHn++ecxffr0Gx7TpUuXWwri7d00T0FhYSF8fHz0+wsLCxEWFqY/pqioqNl5jY2NKCsr059/PUqlEkolO5oRERkbFzsbuNjZINTf5Zr9c0eGiAlFZqFNBY6Hhwc8PDwMEiQ4OBje3t5ITEzUFzQajQaHDx/Wj8SKiopCeXk5UlJSEB4eDgDYtWsXdDodIiMjDZKLiIiITI/B2vqysrKQmpqKrKwsaLVapKamIjU1tdmcNT179sSWLVsANHVImz9/Pt5880389NNPOHnyJKZOnQpfX1+MHz8eANCrVy+MGTMGs2bNQnJyMg4cOIB58+Zh8uTJrR5BRURERObPYJ2MFy5ciHXr1ulf9+/ftOLs7t27MWLECADA+fPnoVar9ccsWLAAVVVVmD17NsrLyzFs2DDEx8dDpfpryu8NGzZg3rx5GDVqFORyOSZMmIDly5cb6jaIiIjIBHGxTc6DQ0REZBLa8vnN7uhERERkdljgEBERkdlhgUNERERmhwUOERERmR0WOERERGR2WOAQERGR2WGBQ0RERGaHBQ4RERGZHRY4REREZHYMtlSDMftz8maNRiM4CREREbXWn5/brVmEwSILnIqKCgCAv7+/4CRERETUVhUVFXB2dr7hMRa5FpVOp0NeXh4cHR0hk8na9doajQb+/v7Izs7mOlf/B9+bG+P7c2N8f26M70/L+N7cmCm9P5IkoaKiAr6+vpDLb9zLxiJbcORyOfz8/Az6PZycnIz+/yii8L25Mb4/N8b358b4/rSM782Nmcr7c7OWmz+xkzERERGZHRY4REREZHZY4LQzpVKJRYsWQalUio5idPje3Bjfnxvj+3NjfH9axvfmxsz1/bHITsZERERk3tiCQ0RERGaHBQ4RERGZHRY4REREZHZY4BAREZHZYYHTjlasWIGgoCCoVCpERkYiOTlZdCSjsW/fPtx///3w9fWFTCbD1q1bRUcyGkuWLMHAgQPh6OgIT09PjB8/HufPnxcdy2h8+umn6Nevn34SsqioKPz666+iYxmld955BzKZDPPnzxcdxSi89tprkMlkzbaePXuKjmVUcnNz8eijj6JTp06wtbVF3759cfToUdGx2gULnHayefNmxMbGYtGiRTh27BhCQ0MRExODoqIi0dGMQlVVFUJDQ7FixQrRUYzO3r17MXfuXBw6dAgJCQloaGjA6NGjUVVVJTqaUfDz88M777yDlJQUHD16FHfffTfGjRuH06dPi45mVI4cOYLPPvsM/fr1Ex3FqNxxxx3Iz8/Xb/v37xcdyWhcuXIFQ4cOhbW1NX799VecOXMG//73v+Hq6io6WvuQqF0MGjRImjt3rv61VquVfH19pSVLlghMZZwASFu2bBEdw2gVFRVJAKS9e/eKjmK0XF1dpS+//FJ0DKNRUVEhdevWTUpISJDuuusu6dlnnxUdySgsWrRICg0NFR3DaL300kvSsGHDRMcwGLbgtIP6+nqkpKQgOjpav08ulyM6OhpJSUkCk5EpUqvVAAA3NzfBSYyPVqvFpk2bUFVVhaioKNFxjMbcuXMxduzYZr+DqMnFixfh6+uLLl26YMqUKcjKyhIdyWj89NNPiIiIwMSJE+Hp6Yn+/fvjiy++EB2r3bDAaQclJSXQarXw8vJqtt/LywsFBQWCUpEp0ul0mD9/PoYOHYo+ffqIjmM0Tp48CQcHByiVSjz55JPYsmULevfuLTqWUdi0aROOHTuGJUuWiI5idCIjI7F27VrEx8fj008/RXp6OoYPH46KigrR0YzC5cuX8emnn6Jbt27YsWMH5syZg2eeeQbr1q0THa1dWORq4kTGau7cuTh16hT7CfwfPXr0QGpqKtRqNb7//ntMmzYNe/futfgiJzs7G88++ywSEhKgUqlExzE699xzj/6/+/Xrh8jISAQGBuLbb7/FzJkzBSYzDjqdDhEREXj77bcBAP3798epU6ewcuVKTJs2TXC628cWnHbg7u4OhUKBwsLCZvsLCwvh7e0tKBWZmnnz5mHbtm3YvXs3/Pz8RMcxKjY2NggJCUF4eDiWLFmC0NBQfPTRR6JjCZeSkoKioiIMGDAAVlZWsLKywt69e7F8+XJYWVlBq9WKjmhUXFxc0L17d6SlpYmOYhR8fHyu+SOhV69eZvMYjwVOO7CxsUF4eDgSExP1+3Q6HRITE9lPgG5KkiTMmzcPW7Zswa5duxAcHCw6ktHT6XSoq6sTHUO4UaNG4eTJk0hNTdVvERERmDJlClJTU6FQKERHNCqVlZW4dOkSfHx8REcxCkOHDr1mSooLFy4gMDBQUKL2xUdU7SQ2NhbTpk1DREQEBg0ahGXLlqGqqgozZswQHc0oVFZWNvurKT09HampqXBzc0NAQIDAZOLNnTsXGzduxI8//ghHR0d9vy1nZ2fY2toKTideXFwc7rnnHgQEBKCiogIbN27Enj17sGPHDtHRhHN0dLymr5a9vT06derEPlwAXnjhBdx///0IDAxEXl4eFi1aBIVCgUceeUR0NKPw3HPPYciQIXj77bfx8MMPIzk5GZ9//jk+//xz0dHah+hhXObk448/lgICAiQbGxtp0KBB0qFDh0RHMhq7d++WAFyzTZs2TXQ04a73vgCQ1qxZIzqaUXj88celwMBAycbGRvLw8JBGjRol/fbbb6JjGS0OE//LpEmTJB8fH8nGxkbq3LmzNGnSJCktLU10LKPy888/S3369JGUSqXUs2dP6fPPPxcdqd3IJEmSBNVWRERERAbBPjhERERkdljgEBERkdlhgUNERERmhwUOERERmR0WOERERGR2WOAQERGR2WGBQ0RERGaHBQ4RERGZHRY4REREZHZY4BAREZHZYYFDREREZocFDhEREZmd/w9nHUhTrfFdxAAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"plt.plot(x, s, linestyle=\"dashed\")\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "b465a6e5-06ab-4fc0-8238-f4f05593a9d1",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-88e04ff7645c08cd",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe - Multiplot\n",
|
||
"\n",
|
||
"*8 Punkte*\n",
|
||
"\n",
|
||
"In der nächsten Aufgabe willst du zwei Funktionen gleichzeitig plotten: $f(x) = \\sqrt{x}, \\; x \\geq 0$ und $g(x) = x^2$. \n",
|
||
"\n",
|
||
"Gehe dabei wie folgt vor: \n",
|
||
"1. Definiere einen geeigneten [Linspace](https://numpy.org/doc/stable/reference/generated/numpy.linspace.html#numpy-linspace) für den Zahlenraum von `0` bis `3`. (Tipp: Achte darauf, dass die Quadratwurzel nur für nicht-negative Zahlen definiert ist.) \n",
|
||
"2. Berechne die Werte für die Quadratwurzel mit [np.sqrt](https://numpy.org/doc/stable/reference/generated/numpy.sqrt.html#numpy.sqrt). \n",
|
||
"3. Berechne die Werte für die Quadratzahlen mit [np.square](https://numpy.org/doc/stable/reference/generated/numpy.square.html#numpy-square). \n",
|
||
"4. Gib den beiden Plots die Farben Grün und Rot. Nutze hierfür die [Color Shorthands](https://matplotlib.org/stable/users/explain/colors/colors.html) aus der Dokumentation. \n",
|
||
"5. Plotte die Quadratfunktion mit dem Linestyle `dashdot`, wie in der Dokumentation zu [Linestyles](https://matplotlib.org/stable/gallery/lines_bars_and_markers/linestyles.html) beschrieben. \n",
|
||
"6. Vergeben angemessene Labels für beide Plots. \n",
|
||
"7. Füge die Legende hinzu. \n",
|
||
"8. Plotte das Ergebnis mit `plt.show()`.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 37,
|
||
"id": "41c07973-1717-48f1-94a5-c6930b0089ec",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-6bb6ab1d60fffde5",
|
||
"locked": false,
|
||
"points": 8,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAhYAAAGdCAYAAABO2DpVAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAATK9JREFUeJzt3Xd4U/XiBvA3aZt0bzqgpWxKoYyyLFxZsmcrskREFEWG2ot4hUe5gOhFRBCuF0VUoAKyLfJj9QKy9yqzUoQChU5KabroSL6/P3IJBNrSlLQn4/08z3nanJwkb46xefmeJRNCCBAREREZgVzqAERERGQ5WCyIiIjIaFgsiIiIyGhYLIiIiMhoWCyIiIjIaFgsiIiIyGhYLIiIiMhoWCyIiIjIaGyr+wU1Gg2Sk5Ph4uICmUxW3S9PRERElSCEQE5ODmrWrAm5vOxxiWovFsnJyQgMDKzulyUiIiIjSEpKQkBAQJn3V3uxcHFxAaAN5urqWt0vT0RERJWgUqkQGBio+x4vS7UXi4ebP1xdXVksiIiIzMyzdmPgzptERERkNCwWREREZDQsFkRERGQ01b6PRUWo1WoUFxdLHYOskI2NDWxtbXkoNBFRJZlcscjNzcXt27chhJA6ClkpR0dH+Pv7Q6FQSB2FiMjsmFSxUKvVuH37NhwdHVGjRg3+q5GqlRACRUVFyMjIQGJiIho2bFjuSWCIiOhpJlUsiouLIYRAjRo14ODgIHUcskIODg6ws7PDzZs3UVRUBHt7e6kjERGZFZP85xhHKkhKHKUgIqo8/gUlIiIio2GxICIiIqNhsTCCjIwMjB8/HrVr14ZSqYSfnx969eqFw4cPSx2t0vbt2weZTKabatSogb59++LChQtGfZ0VK1bA3d3dqM9JRETSMamdN83V4MGDUVRUhOjoaNSrVw9paWnYs2cPMjMzpY6GoqKi5zps8sqVK3B1dUVycjI++ugj9OvXD3/99RcPxSQiolJxxOI53b9/HwcPHsTcuXPRtWtXBAUFoV27dpg2bRoGDhyoW+7q1avo1KkT7O3tERISgl27dkEmk2Hz5s0AHo0Q3L9/X/eYuLg4yGQy3LhxAwCQmZmJESNGoFatWnB0dERoaCjWrFmjl6dLly6YNGkSoqKi4O3tjV69egEALl68iD59+sDZ2Rm+vr4YNWoU7t69+8z35+PjAz8/P4SFhSEqKgpJSUn4888/dfdv2rQJTZs2hVKpRJ06dTB//ny9x2dlZeH111+Hh4cHHB0d0adPH1y9elX3nseMGYPs7GzdyMjMmTMruuqJiOgJJZoSqSOYeLEQAsjLk2aq4Am6nJ2d4ezsjM2bN6OwsLDUZTQaDV5++WUoFAocP34cS5Yswccff2zw6njw4AFat26Nbdu24eLFi3jnnXcwatQonDhxQm+56OhoKBQKHD58GEuWLMH9+/fRrVs3tGrVCqdOncLOnTuRlpaGoUOHVvi1s7OzsXbtWgDQjVacPn0aQ4cOxfDhw3HhwgXMnDkT06dPx4oVK3SPe+ONN3Dq1Cls2bIFR48ehRACffv2RXFxMTp06ICFCxfC1dUVKSkpSElJwZQpUwxeL0REBBy8eRDNvmuGw7ck3gwvqll2drYAILKzs5+6r6CgQFy+fFkUFBRoZ+TmCqH9iq/+KTe3wu9p48aNwsPDQ9jb24sOHTqIadOmiXPnzunuj42NFba2tuLOnTu6eTt27BAARExMjBBCiL179woAIisrS7fM2bNnBQCRmJhY5mv369dPfPjhh7rbnTt3Fq1atdJbZvbs2aJnz55685KSkgQAceXKlVKf92EeJycn4eTkJAAIAGLgwIG6ZV599VXRo0cPvcd99NFHIiQkRAghREJCggAgDh8+rLv/7t27wsHBQaxfv14IIcTy5cuFm5tbme9PCk99DomITFxuYa6ov6i+wEyINze/WSWvUd739+NMe8TCTAwePBjJycnYsmULevfujX379iEsLEz3L/f4+HgEBgaiZs2auseEh4cb/DpqtRqzZ89GaGgoPD094ezsjNjYWNy6dUtvudatW+vdPnfuHPbu3asbXXF2dkZwcDAA4Nq1a+W+5sGDB3H69GmsWLECjRo1wpIlS3T3xcfHo2PHjnrLd+zYEVevXoVarUZ8fDxsbW3Rvn173f1eXl5o3Lgx4uPjDX7/RERUuo93f4xrWdcQ6BqIBb0WSJrFtHfedHQEcnOle20D2Nvbo0ePHujRowemT5+OsWPHYsaMGXjjjTcq9PiHJ2USj22CefJCbPPmzcOiRYuwcOFChIaGwsnJCVFRUSgqKtJbzsnJSe92bm4uBgwYgLlz5z71uv7+/uXmqlu3Ltzd3dG4cWOkp6dj2LBhOHDgQIXeExERVb091/dg8cnFAICfB/4MN3s3SfOYdrGQyYAnviTNRUhIiG7HzCZNmiApKQkpKSm6L/Jjx47pLV+jRg0AQEpKCjw8PABod9583OHDhzFo0CC89tprALT7biQkJCAkJKTcLGFhYdi0aRPq1KkDW9vK/yefOHEi5syZg5iYGERGRqJJkyZPHVJ7+PBhNGrUCDY2NmjSpAlKSkpw/PhxdOjQAYB2B9QrV67oMisUCqjV6kpnIiKyZqpCFd7c8iYA4N3W76JH/R4SJzL1nTfNQGZmJrp164ZVq1bh/PnzSExMxIYNG/DVV19h0KBBAIDu3bujUaNGGD16NM6dO4eDBw/ik08+0XueBg0aIDAwEDNnzsTVq1exbdu2p46waNiwIXbt2oUjR44gPj4e48aNQ1pa2jMzTpw4Effu3cOIESNw8uRJXLt2DbGxsRgzZoxBX+qOjo54++23MWPGDAgh8OGHH2LPnj2YPXs2EhISEB0djf/85z+6HTAbNmyIQYMG4e2338ahQ4dw7tw5vPbaa6hVq5Zu3dSpUwe5ubnYs2cP7t69i/z8/ArnISKydh/Gfohb2bdQ170u5vWcJ3UcrSrZw6McBu28aQYePHggpk6dKsLCwoSbm5twdHQUjRs3Fp9++qnIz8/XLXflyhXxt7/9TSgUCtGoUSOxc+dOvZ03hRDi0KFDIjQ0VNjb24sXX3xRbNiwQW/nzczMTDFo0CDh7OwsfHx8xKeffipef/11MWjQIN1zdO7cWXzwwQdP5UxISBCRkZHC3d1dODg4iODgYBEVFSU0Gk2p76u0nUmFEOLWrVvC1tZWrFu3Tgih3XE1JCRE2NnZidq1a4t58+bpLX/v3j0xatQo4ebmJhwcHESvXr1EQkKC3jLvvvuu8PLyEgDEjBkzyl/h1cAcP4dEZH22J2wXmAmBmRD7EvdV+etVdOdNmRAVPK7SSFQqFdzc3JCdnQ1XV1e9+x48eIDExETUrVvXKq4qKZPJEBMTg4iICKmj0GOs7XNIROYnqyALzb5vhuScZHzQ/gMs7L2wyl+zvO/vx3FTCBERkZnZmrAVyTnJaOTVCP966V9Sx9Fj2jtvEhER0VNGtRgFfxd/uCpd4Whn2FGMVY3FQkLVvBWKiIgsSPd63aWOUCpuCiEiIjIDQgjM2jcLN+7fkDpKuVgsiIiIzMAv537BzP0z0WZpG+QU5kgdp0zcFEJERGQGXgx6EX+r/Tf0a9gPLkoXqeOUicWCiIjIDNTzqId9o/dJHeOZuCmEiIjIhKXkpOh+t5HbwEZuI2GaZ2OxICIiMlGX0i+h/r/r4+87/45idfGzH2ACWCzIrMycORMtW7aUOgYRUZUrUhdhVMwoFJQUIOFeAmzl5rH3AouFEWRkZGD8+PGoXbs2lEol/Pz80KtXr6eu/GlO9u3bB5lM9tT06aefVlsGmUymu0LsQ1OmTMGePXuqLQMRkVQ+2/8ZzqaehZeDF34a8BNkMpnUkSrEPOqPiRs8eDCKiooQHR2NevXqIS0tDXv27EFmZqbU0VBUVASFQlHpx1+5ckXvnPDOzs7GiFVpzs7OkmcgIqpqx24fw5xDcwAAS/ovgb+Lv8SJKo4jFs/p/v37OHjwIObOnYuuXbsiKCgI7dq1w7Rp0zBw4EDdclevXkWnTp1gb2+PkJAQ7Nq1S+9f5A9HCO7fv697TFxcHGQyGW7cuAFAe4n2ESNGoFatWnB0dERoaCjWrFmjl6dLly6YNGkSoqKi4O3tjV69egEALl68iD59+sDZ2Rm+vr4YNWoU7t69+8z35+PjAz8/P93k7OxcoawrVqyAu7s7YmNj0aRJEzg7O6N3795ISUnRe/5ly5ahadOmUCqV8Pf3x6RJkwBoL6cOAJGRkZDJZLrbT24K0Wg0+OyzzxAQEAClUomWLVti586duvtv3LgBmUyG3377DV27doWjoyNatGiBo0ePPvO9ExFJIa8oD6NiRkEjNBgZOhKvhLwidSSDmEWxyCvKM3gq0ZToHl+iKUFeUR4Kigsq9LyGePgv6M2bN6OwsLDUZTQaDV5++WUoFAocP34cS5Yswccff2zwenjw4AFat26Nbdu24eLFi3jnnXcwatQonDhxQm+56OhoKBQKHD58GEuWLMH9+/fRrVs3tGrVCqdOncLOnTuRlpaGoUOHGpzBEPn5+fj666+xcuVKHDhwALdu3cKUKVN093///feYOHEi3nnnHVy4cAFbtmxBgwYNAAAnT54EACxfvhwpKSm6209atGgR5s+fj6+//hrnz59Hr169MHDgQFy9elVvuU8++QRTpkxBXFwcGjVqhBEjRqCkpKTU5yQiktJHuz7CX/f+QoBrAP7T9z9SxzFclV/A/QnlXc+9oKBAXL58WRQUFOjNf3i9eUOm9RfX6x6//uJ6gZkQnZd31nte76+8S32soTZu3Cg8PDyEvb296NChg5g2bZo4d+6c7v7Y2Fhha2sr7ty5o5u3Y8cOAUDExMQIIYTYu3evACCysrJ0y5w9e1YAEImJiWW+dr9+/cSHH36ou925c2fRqlUrvWVmz54tevbsqTcvKSlJABBXrlwp9Xkf5nFyctKb7t69W6Gsy5cvFwDEX3/9pVtm8eLFwtfXV3e7Zs2a4pNPPinzvT2+fh6aMWOGaNGihd5zfPHFF3rLtG3bVkyYMEEIIURiYqIAIH766Sfd/ZcuXRIARHx8fKmvW9bnkIioqu28ulP3XbTr2i6p4+gp7/v7cWYxYmHqBg8ejOTkZGzZsgW9e/fGvn37EBYWhhUrVgAA4uPjERgYiJo1a+oeEx4ebvDrqNVqzJ49G6GhofD09ISzszNiY2Nx69YtveVat26td/vcuXPYu3evbnTF2dkZwcHBAIBr166V+5oHDx5EXFycbvLw8KhwXkdHR9SvX19329/fH+np6QCA9PR0JCcn46WXXqrw8z1JpVIhOTkZHTt21JvfsWNHxMfH681r3ry5Xo6HGYiITMW9gnsY8/sYAMB77d4z2YuMPYtZ7LyZOy3X4McobZW63yObRCJ3Wi7kMv0edeODG88bTcfe3h49evRAjx49MH36dIwdOxYzZszAG2+8UaHHy+XabOKxK54WF+sfszxv3jwsWrQICxcuRGhoKJycnBAVFYWioiK95ZycnPRu5+bmYsCAAZg7d+5Tr/vwS7YsdevWhbu7u8FZAcDOzk7vtkwm0z3GwcGh3Nc1tsezPNyzWqPRVGsGIqLyTNg2ASm5KWjs1Rhfdv9S6jiVZhbFwknh9OyFymErt4Wt4um3+rzPW56QkBDdjplNmjRBUlISUlJSdF/kx44d01u+Ro0aAICUlBTdqEBcXJzeMocPH8agQYPw2muvAdB+MSYkJCAkJKTcLGFhYdi0aRPq1KkDW9vn/09ekazP4uLigjp16mDPnj3o2rVrqcvY2dlBrVaX+Ryurq6oWbMmDh8+jM6dO+vmHz58GO3atTMoDxGRlNZeXIt1l9bBRmaDlZEr4WjnKHWkSuOmkOeUmZmJbt26YdWqVTh//jwSExOxYcMGfPXVVxg0aBAAoHv37mjUqBFGjx6Nc+fO4eDBg/jkk0/0nqdBgwYIDAzEzJkzcfXqVWzbtg3z58/XW6Zhw4bYtWsXjhw5gvj4eIwbNw5paWnPzDhx4kTcu3cPI0aMwMmTJ3Ht2jXExsZizJgx5X5xl6UiWSti5syZmD9/Pv7973/j6tWrOHPmDL799lvd/Q+LR2pqKrKyskp9jo8++ghz587FunXrcOXKFUydOhVxcXH44IMPDM5DRCSFInURpvxXu2P7p50+RdtabSVO9HxYLJ6Ts7Mz2rdvj2+++QadOnVCs2bNMH36dLz99tv4z3+0e/PK5XLExMSgoKAA7dq1w9ixY/HFF1/oPY+dnR3WrFmDP//8E82bN8fcuXPx+eef6y3z6aefIiwsDL169UKXLl3g5+eHiIiIZ2Z8+K96tVqNnj17IjQ0FFFRUXB3d9dt1jBERbJWxOjRo7Fw4UJ89913aNq0Kfr37693NMf8+fOxa9cuBAYGolWrVqU+x/vvv4/Jkyfjww8/RGhoKHbu3IktW7agYcOGBuchIpKCwkaBXaN24c2Wb+KTFz959gNMnEw8vqG8GqhUKri5uSE7O1vvxEuA9nDKxMRE1K1bF/b29tUZSxIymQwxMTEVKgdUfaztc0hEVBHlfX8/jiMWREREEjiXeg6Hb5nvpR/KwmJBRERUzfKL8zFi0wh0WtEJay+ulTqOUZnFUSGWqpq3QhERkYnQCA3a1mqLrAdZZnu+irKwWBAREVUzZ4UzoiOikZ6XDm9Hb6njGBU3hRAREVWTvKI8vdFqHycfCdNUDYOKhVqtxvTp01G3bl04ODigfv36mD17ttGH9LmJgKTEzx8RVQUhBIZtHIYBawYgPc9yLylg0KaQuXPn4vvvv0d0dDSaNm2KU6dOYcyYMXBzc8P777//3GFsbGwAAEVFRdV+ymeih/Lz8wE8fUpyIqLnseTUEmy7ug1KGyXSctMscrQCMLBYHDlyBIMGDUK/fv0AaM+MuGbNmqcu213pMLa2cHR0REZGBuzs7Cp18iaiyhJCID8/H+np6XB3d9cVXSKi5xWfEY8P//shAODL7l8i1DdU4kRVx6Bi0aFDByxduhQJCQlo1KgRzp07h0OHDmHBggVlPqawsBCFhYW62yqVqsxlZTIZ/P39kZiYiJs3bxoSjcho3N3d4efnJ3UMIrIQReoijPxtJApKCtCzfk+83/75R/hNmUHFYurUqVCpVAgODoaNjQ3UajW++OILjBw5sszHzJkzB7NmzarwaygUCjRs2PCpK3YSVQc7OzuOVBCRUU3/YzrOpp6Fl4MXVgxa8dSVti2NQcVi/fr1WL16NX799Vc0bdoUcXFxiIqKQs2aNTF69OhSHzNt2jRMnjxZd1ulUiEwMLDc15HL5TyVMhERmb29iXsx78g8AMBPA3+Cv4u/xImqnkHF4qOPPsLUqVMxfPhwAEBoaChu3ryJOXPmlFkslEollErl8yclIiIyI1kFWXh98+sQEHg77G1EBEdIHalaGDQek5+f/9QOlTY2NtBoNEYNRUREZM6EEBi3dRxuq26joWdDfNPrG6kjVRuDRiwGDBiAL774ArVr10bTpk1x9uxZLFiwAG+++WZV5SMiIjI70eeiseHyBtjKbbH65dVwUjhJHanaGFQsvv32W0yfPh0TJkxAeno6atasiXHjxuGf//xnVeUjIiIyKwmZCZi0fRIAYFaXWWhbq63EiaqXTFTzaQYrej13IiIiczRgzQBsTdiKrnW6YteoXbCRW8aRZhX9/rbsY16IiIiq2fJBy/F6i9exMnKlxZQKQ/DqpkREREbk7eiN6IhoqWNIhiMWREREzyklJwWrzq/iRQzBEQsiIqLnohEajIoZhT2Je/DXvb8ws8tMqSNJiiMWREREz0EIgW51u8FV6YrhzYZLHUdyPCqEiIjICO4V3IOng6fUMaoMjwohIiKqQjmFOSgoLtDdtuRSYQgWCyIiIgMJIfDO1nfQ7qd2uJxxWeo4JoU7bxIRERko+lw01l5cCxuZDVSFKqnjmBSOWBARERngyt0rmLh9IgBgdtfZeCHgBYkTmRYWCyIiogoqLCnE8E3DkV+cj251u+EfHf8hdSSTw2JBRERUQVN3T0Vcahy8Hb2t9pTdz8JiQUREVAHbErZh4fGFAIAVg1agpktNaQOZKBYLIiKiZ7ituo3Rm0cDAD5o/wH6NeoncSLTxWJBRERUjhJNCUZsGoHMgkyE+Yfhy+5fSh3JpLFYEBERleOfe/+JQ7cOwVXpivWvrIe9rb3UkUwaiwUREVEZdv61E3MOzQEA/DTgJ9T3rC9xItPHYkFERFSG/5z4DwBgQpsJGNJ0iMRpzAPPvElERFSG34b9hn8f/zcmtZskdRSzwWJBRERUBoWNAlM6TJE6hlnhphAiIqLH/PfafzFt9zSUaEqkjmKWOGJBRET0P6pCFV777TVk5GfAy9GLoxWVwBELIiKi/3FVumJx38XoFNSJ+1VUkkwIIarzBVUqFdzc3JCdnQ1XV9fqfGkiIqIKEUJAJpNJHcOkVPT7myMWRERk9Y7fPo6UnBTdbZaKymOxICIiq5aSk4KBawei5Q8tcSHtgtRxzB6LBRERWS21Ro1Xf3sV6Xnp8HXyRQPPBlJHMnssFkREZLU+2/8Z9t3YByc7J2wYsgEOdg5SRzJ7LBZERGSVdl3bhdkHZgMAfuj/Axp7N5Y4kWVgsSAiIquTlJ2EEZtGQEDg7bC3MbL5SKkjWQwWCyIisipF6iIM2TAEmQWZCPMPw7/7/FvqSBaFxYKIiKzKlP9OwfE7x+Fu746NQzbC3tZe6kgWhcWCiIisxtqLa/HtiW8BACsjV6KuR12JE1keFgsiIrIK8RnxGLtlLABg2t+moX+j/hInskwsFkREZPFyi3LxyoZXkFech651uuKzrp9JHcli8eqmRERkFUJ9QpFVkIU1g9fAVs6vv6rCNUtERBbPWeGMNYPXIDknGb7OvlLHsWjcFEJERBYrOScZDy/iLZPJUMu1lsSJLB+LBRERWaS7+Xfxwk8v4JUNr0BVqJI6jtVgsSAiIot0NOkoUnNTecXSasZ9LIiIyCINaDwAB8cchKOdI1yVrlLHsRosFkREZFGEEJDJZACA9gHtJU5jfbgphIiILMat7FsI/zkccalxUkexWiwWRERkER6UPMDg9YNx/M5xvLfjPd3RIFS9WCyIiMjsCSEwYdsEnEo+BU8HT6yMXKnbHELVi8WCiIjM3g+nf8DyuOWQy+RYO3gt6rjXkTqS1WKxICIis3Y06Sje3/E+AOBf3f6FHvV7SJzIurFYEBGR2UrJScHg9YNRrCnGKyGv4B8d/yF1JKvHYkFERGapSF2EIRuGICU3BSE1QrBs4DLuV2ECWCyIiMgsTY6djMNJh+GqdEXMsBi4KF2kjkRgsSAiIjMUHReNxScXAwBWv7wajbwaSZyIHmKxICIis3I6+TTGbR0HAJjReQb6N+ovcSJ6HIsFERGZlcUnF6NQXYj+jfrjn53/KXUcegKvFUJERGblxwE/orFXY4xrMw5yGf99bGpYLIiIyKzYyG3w8d8+ljoGlYFVj4iITN76S+vx7tZ3UVhSKHUUegaOWBARkUm7V3APY7eMRU5RDpr5NMOkdpOkjkTl4IgFERGZNE8HT6x7ZR2GhAzBu23elToOPYNMVPN1ZVUqFdzc3JCdnQ1XV9fqfGkiIiKqpIp+f3PEgoiITNL8I/NxPeu61DHIQCwWRERkcpafXY4pu6ag3Y/tcK/gntRxyAAsFkREZFKOJh3Fu9u0+1JMajcJng6eEiciQ7BYEBGRybituo3IdZEoUhchMjiSZ9Y0QwYXizt37uC1116Dl5cXHBwcEBoailOnTlVFNiIisiIFxQWIWBuBtLw0hPqE4pfIX3hmTTNk0HkssrKy0LFjR3Tt2hU7duxAjRo1cPXqVXh4eFRVPiIisgJCCIz9v7E4nXIaXg5e+H3473BWOEsdiyrBoGIxd+5cBAYGYvny5bp5devWNXooIiKyLvOOzMOvF36FrdwWG4duRF0PfreYK4PGmLZs2YI2bdpgyJAh8PHxQatWrfDjjz+W+5jCwkKoVCq9iYiI6KHtV7dj6u6pAIBFvRehS50u0gai52JQsbh+/Tq+//57NGzYELGxsRg/fjzef/99REdHl/mYOXPmwM3NTTcFBgY+d2giIrIMf979EyM2jYCAwDth72B8m/FSR6LnZNCZNxUKBdq0aYMjR47o5r3//vs4efIkjh49WupjCgsLUVj46KIxKpUKgYGBPPMmEZGVu//gPtr/1B4JmQl4sfaL2P36bihsFFLHojJUyZk3/f39ERISojevSZMmuHXrVpmPUSqVcHV11ZuIiIi+OPAFEjITUNutNjYO3chSYSEM2nmzY8eOuHLlit68hIQEBAUFGTUUERFZvtndZiOnKAfjWo+Dj5OP1HHISAwqFn//+9/RoUMH/Otf/8LQoUNx4sQJLF26FEuXLq2qfEREZKHsbe2xpP8SqWOQkRm0KaRt27aIiYnBmjVr0KxZM8yePRsLFy7EyJEjqyofERFZkP039mPa7mnQCI3UUaiKGDRiAQD9+/dH//79qyILERFZsPsP7mPw+sHILMiEj5MP/h7+d6kjURXguVKJiKhauNu7Y1HvRegU1AnvtnlX6jhURQw63NQYKnq4ChERWSYhBGQymdQxyEBVcrgpERGRIYQQmH9kPlJyUnTzWCosG4sFERFVmW9PfIspu6Yg/Odw5BXlSR2HqgGLBRERVYkdV3fg77HaHTQntZsEJ4WTxImoOrBYEBGR0V1Mv4hhG4dBIzR4q9Vb+DD8Q6kjUTVhsSAiIqNKz0tH/1/7I6coB52DOuO7ft9xvworwmJBRERG86DkASLWRuBm9k008GyATUM38RogVobFgoiIjEIIgbFbxuLo7aNwt3fH1hFb4eXoJXUsqmYsFkREZBRfHPwCqy+shq3cFhuHbERj78ZSRyIJsFgQEdFzW3dxHabvnQ4A+K7vd3ip3ksSJyKpsFgQEdFzOXTrEEZvHg0A+PsLf8fbrd+WOBFJicWCiIgqTQiBGftmoFBdiIjgCMzrMU/qSCQxFgsiIqo0mUyGmGEx+DD8Q6x+eTVs5DZSRyKJGXzZdCIioscvJOaqdMXXPb+WOBGZCo5YEBGRQTRCgxGbRmDe4Xmo5gtkkxlgsSAiIoNsTdiKdZfW4ZM/PkFCZoLUccjEcFMIEREZZGDjgVjYayE8HTx5rgp6CosFEREZ7IMXPpA6ApkobgohIqJnikuNQ8TaCNx/cF/qKGTiWCyIiKhcSdlJ6PdrP/x+5XdM3T1V6jhk4lgsiIioTPcf3Eef1X2QnJOMkBoh+LL7l1JHIhPHYkFERKV6eAn0SxmX4O/sj+2vboe7vbvUscjEsVgQEdFTNEKD12Nex/6b++GicMGOkTsQ5B4kdSwyAywWRESkRwiBybGTseHyBtjJ7RAzLAYt/FpIHYvMBIsFERHpWXB0ARYdXwQAWBGxgpdAJ4OwWBARkc6aC2swZdcUAMC8HvPwauirEicic8NiQUREAIA/Ev/A6M2jAQAftP8AH4Z/KHEiMkcsFkREhHOp5xC5LhLFmmIMCRmCBb0W6K5eSmQIntKbiIhgb2sPTwdPtPRriV8if4Fcxn93UuWwWBARERp7N8bRt45CaaOEva291HHIjLGSEhFZqfzifBy6dUh328/ZDx4OHhImIkvAYkFEZIWK1cUYumEoukZ3xbqL66SOQxaExYKIyAoJCLgqXWErt0WAa4DUcciCcB8LIiIrpLBRYNXLq3Ap/RJCfUOljkMWhCMWRERWZPf13dAIDQBALpOzVJDRsVgQEVmJ5WeXo8fKHnh106tQa9RSxyELxWJBRGQFtlzZgrH/NxYAEOQWBBu5jcSJyFKxWBARWbgDNw9g2MZh0AgNxrQcgy+7fyl1JLJgLBZERBbsXOo5DFgzAA9KHmBg44FYOmApT9VNVYrFgojIQl3Puo5eq3pBVajCi7VfxNrBa2Er58GAVLVYLIiILNAd1R10/6U70vLS0Ny3ObaM2AIHOwepY5EVYLEgIrIwd/Pvoueqnki8n4j6HvWxc+ROuNu7Sx2LrASLBRGRBVEVqtB7VW9czriMWi61sPv13fB38Zc6FlkRFgsiIgtRUFyAAWsG4HTKaXg7emP367tRx72O1LHIyrBYEBFZiIvpF3Eq+RRcla6IfS0Wwd7BUkciK8Tdg4mILETbWm2xa9QuaIQGYf5hUschK8ViQURkxoQQSMlNQU2XmgCADoEdJE5E1o6bQoiIzJQQAlP+OwUtl7TE2ZSzUschAsBiQURktvKL87Hv5j5k5GfgQvoFqeMQAeCmECIis+WkcMIfr/+B2GuxGNp0qNRxiABwxIKIyOxczris+93N3o2lgkwKiwURkRmJjotGs++aYcHRBVJHISoViwURkZlYc2EN3tzyJgQEbt6/CSGE1JGInsJiQURkBn6L/w2jYkZBIzR4J+wdLOy9kJc/J5PEYkFEZOK2JWzD8I3DoRZqjG4xGt/3/56lgkwWiwURkQnbdW0XBq8fjGJNMYY1HYafB/4MuYx/usl08dNJRGSi9t/Yj0FrB6FQXYiI4AisjFwJG7mN1LGIysViQURkgo4mHUW/X/uhoKQAfRv2xdrBa2FnYyd1LKJnYrEgIjIxp5NPo/fq3sgrzsNLdV/CpqGboLRVSh2LqEJYLIiITMiZlDPosbIHVIUqvFj7Rfw+/HfY29pLHYuowlgsiIhMyMk7J5H1IAvhAeHY+upWOCmcpI5EZBBeK4SIyISMazMOHg4e6N2gN1yVrlLHITIYRyyIiCR2Ie0CsgqydLeHNh3KUkFm67mKxZdffgmZTIaoqCgjxSEisi5xqXHoEt0F3Vd2x72Ce1LHIXpulS4WJ0+exA8//IDmzZsbMw8RkVWxldvCRmYDO7kdbGQ8RwWZv0oVi9zcXIwcORI//vgjPDw8jJ2JiMhqNPNphoNjDiL2tVi42btJHYfouVWqWEycOBH9+vVD9+7dn7lsYWEhVCqV3kREZM3Op53Hvhv7dLcbezdmqSCLYfBRIWvXrsWZM2dw8uTJCi0/Z84czJo1y+BgRESW6HzaeXSL7ob84nz8MfoPvBDwgtSRiIzKoBGLpKQkfPDBB1i9ejXs7St2wpZp06YhOztbNyUlJVUqKBGRuTubchbdorshsyATzXyaIdg7WOpIREYnE0KIii68efNmREZGwsbm0Q5GarUaMpkMcrkchYWFeveVRqVSwc3NDdnZ2XB15eFURGQdTtw5gV6reuH+g/toV6sdYl+Lhbu9u9SxiCqsot/fBm0Keemll3DhwgW9eWPGjEFwcDA+/vjjZ5YKIiJrdCTpCHqv6o2cohx0DOyI7SO38zwVZLEMKhYuLi5o1qyZ3jwnJyd4eXk9NZ+IiLSXPu/3az/kFeehS50u+L8R/wdnhbPUsYiqDM+8SURURXZf340+q/sgrzgPPer1wLZXt7FUkMV77muF7Nu3zwgxiIgsy46rOxC5LhKF6kL0bdgXm4Zu4lVKySpwxIKIyMi2XNmCiHURKFQXYlDjQfht6G8sFWQ1eHVTIiIjOnHnBAavH4wSTQmGhAzB6pdXw87GTupYRNWGxYKIyIha+7fGsKbDICAQHRENWzn/zJJ14SeeiMgIhBCQyWSwkdtgRcQKyKD9ncjacB8LIqLnNP/IfIyKGQWN0AD43xVLWSrISnHEgojoOVzNvIqpe6aiRFOCV0JeQURwhNSRiCTFYkFE9BwaejXEqshVuJ51naWCCCwWREQGU2vUSMtLQ02XmgCAYc2GSZyIyHRwHwsiIgMUqYswYtMIdPi5A26rbksdh8jkcMSCiKiCCooLMHj9YOz4awfs5HY4n3YeAa4BUsciMiksFkREFaAqVGHgmoHYf3M/HGwdEDMsBr0a9JI6FpHJYbEgInqGjLwM9P21L04ln4Kr0hVbR2zFi0EvSh2LyCSxWBARlePm/ZvouaonEjIT4OXghdjXYtG6ZmupYxGZLBYLIqIyXEq/hJ6reiI5Jxm13Woj9rVYBHsHSx2LyKSxWBARleJI0hH0/7U/sh5kIaRGCGJfi+WOmkQVwMNNiYiesP3qdnT/pTuyHmQhPCAcB8ccZKkgqiCOWBARPWbnXzsxcM1AqIUafRv2xYYhG+Bo5yh1LCKzwWJBRPSYDoEdEOobimY+zbBs4DLY2dhJHYnIrLBYEJHVe3jJcwBwVbpi7+i9cFW6Qi7j1mIiQ/H/GiKyasXqYozdMhZfH/laN8/d3p2lgqiSOGJBRFbt/xL+D8vilsFGZoPI4EjU96wvdSQis8ZiQURW7eUmL2Pa36YhPCCcpYLICFgsiMjqJGQmwMfJB+727gCAf730L2kDEVkQbkQkIqty+NZhhP8cjpfXvYwidZHUcYgsDosFEVmN3+J/Q/eV3XGv4B7yivOQW5QrdSQii8NiQURW4dvj3+KV9a/gQckDDGg0AH+8/gc8HTyljkVkcVgsiMiiaYQG/9j1D7y/830ICLzb+l38Nuw3OCmcpI5GZJG48yYRWawHJQ8w5vcxWHtxLQBgzktz8HHHj3UnwyIi42OxICKLlJGXgYh1ETiSdAS2clssG7gMo1qMkjoWkcVjsSAiixOfEY9+v/ZD4v1EuNu7Y9PQTehWt5vUsYisAosFEVmUPdf3YPD6wcguzEY9j3rY9uo2BHsHSx2LyGqwWBCRxSjRlGDi9onILsxGh8AO2DxsM2o41ZA6FpFV4VEhRGQxbOW22Dx8M94Jewd7Xt/DUkEkARYLIjJr+cX52H19t+52sHcwfhjwA+xt7SVMRWS9WCyIyGypClXoGt0VfVb3wZ7re6SOQ0RgsSAiM+aicEF9j/pwVbrCzsZO6jhEBO68SURmSCM0kMvkkMlkWDZoGZJzklHPo57UsYgIHLEgIjMihMDs/bMxZMMQaIQGAGBva89SQWRCOGJBRGYhvzgfb2x+AxsubwAA7Li6A/0a9ZM4FRE9icWCiExeUnYSBq0dhLOpZ2Ent8N3/b5jqSAyUSwWRGTSjiYdReS6SKTlpcHb0Ru/Df0NLwa9KHUsIioDiwURmazouGi8s/UdFKmL0Ny3OX4f/jvquNeROhYRlYM7bxKRySnRlGDKf6fgjd/fQJG6CJHBkTj85mGWCiIzwBELIjIpd/PvYsSmEbqzaU7vNB0zu8yEXMZ/BxGZAxYLIjIZZ1POInJdJG5m34STnROWDVqGoU2HSh2LiAzAYkFEJqFEU4KhG4fiZvZN1Peoj83DN6OZTzOpYxGRgTi2SEQmwVZui1WRqxAZHImTb59kqSAyUywWRCSZtNw0xP4Vq7vdPqA9fhv2GzwcPCRMRUTPg8WCiCRx4/4NhC0NQ+S6SMSlxkkdh4iMhMWCiCQR6BqI5r7NEeQeBAdbB6njEJGRcOdNIqo2+cX5kEEGBzsH2MhtsGbwGshlcrgqXaWORkRGwhELIqoWVzOvIvzncEzaPkk3z93enaWCyMJwxIKIqtzGyxvx5u9vIqcoB6m5qUjNTYWfs5/UsYioCnDEgoiqTJG6CFE7ozBkwxDkFOXgxdov4uy4sywVRBaMIxZEVCVuZd/CsI3DcOz2MQDAxx0/xufdPoetnH92iCwZ/w8nIqPb+ddOvPbba8gsyIS7vTt+ifgFAxoPkDoWEVUDFgsiMhq1Ro1Z+2fh8wOfQ0CgtX9rbBiyAXU96kodjYiqCYsFERnFbdVtvPbba9h/cz8AYHyb8VjQawHsbe0lTkZE1YnFgoie24GbB/DyupeRWZAJZ4UzlvRbgpHNR0odi4gkwGJBRM8tyC0IaqFGmH8Y1g5ei4ZeDaWOREQSYbEgokq5V3APng6eAIAg9yDsHb0XTbybQGmrlDgZEUmJ57EgIoOtPr8adRbWwfar23XzWvq1ZKkgIhYLIjLc8TvHkVOUg+Vxy6WOQkQmhptCiKhCNEIDuUz7b5GvenyFYO9gjGs9TuJURGRqDBqxmDNnDtq2bQsXFxf4+PggIiICV65cqapsRGQC1Bo1vjz0JV765SWUaEoAAPa29pjQdgJs5DYSpyMiU2NQsdi/fz8mTpyIY8eOYdeuXSguLkbPnj2Rl5dXVfmISEI3799E1+iumLZnGvbd2IeY+BipIxGRiZMJIURlH5yRkQEfHx/s378fnTp1qtBjVCoV3NzckJ2dDVdXXi6ZyBQJIfDrhV8xYfsEqApVcFY449s+32J0i9GQyWRSxyMiCVT0+/u59rHIzs4GAHh6epa5TGFhIQoLC/WCEZHpyirIwoTtE7D24loAQHhAOFZGrkR9z/oSJyMic1Dpo0I0Gg2ioqLQsWNHNGvWrMzl5syZAzc3N90UGBhY2Zckoiq2N3Evmi9pjrUX18JGZoPPunyGA2MOsFQQUYVVelPI+PHjsWPHDhw6dAgBAQFlLlfaiEVgYCA3hRCZkMKSQnz6x6eYf3Q+BAQaeDbAqshVaB/QXupoRGQiqnRTyKRJk7B161YcOHCg3FIBAEqlEkolT5pDZKpOJ5/G6M2jcSnjEgDg7bC3saDXAjgrnCVORkTmyKBiIYTAe++9h5iYGOzbtw916/JSyETmbPvV7Ri4ZiDUQo0ajjWwdMBSRARHSB2LiMyYQcVi4sSJ+PXXX/H777/DxcUFqampAAA3Nzc4ODhUSUAiqjqdgzojyD0Irf1bY3HfxajhVEPqSERk5gzax6Ksw8yWL1+ON954o0LPwcNNiaRToinB6vOrMarFKN1ZNDPzM+Hl6CVxMiIydVWyj8VznPKCiCQmhECPlT2w78Y+qApVeK/9ewDAUkFERsWLkBFZCZlMhiEhQ+Bu785NHkRUZZ7rzJuVwU0hRNXnfNp55BblokNgBwDaC4ndzb8LHycfiZMRkdEIAeTlAffuAZmZ2qlbN0Bu3LGDajnzJhGZpgclD/D5gc8x9/BcBLgG4OL4i3BSOEEuk7NUEJmykhL9gvD4VNb8zEygqEj/ee7eBbyk2czJYkFkYQ7dOoSxW8biSqb2ysMt/VqioKQATgoniZMRWREhgJycZxeCJ0vD/y6VUSkKhbZMeHoCBQXGey8GYrEgshCqQhWm7Z6G7059BwDwdfLF4r6LMThksMTJiMxcUVH55aC0++7dA4qLK/+a7u7akvDk5OlZ+nwvL8DJCTCBiwSyWBBZgG0J2/DutndxW3UbAPBmyzfxdc+v4eHgIXEyIhPz4IF2M0FZU2kFISen8q9nb1+xUvD4Mh4egK35fj2bb3IiQnpeOqJ2RmHNxTUAgHoe9bC0/1K8VO8liZMRVYPiYu0Xf3lF4e5dICPj0e95eZV7LZlM+4X/rFLw5DxHR+O+ZzPAYkFkhjRCg6Wnl2Lanmm4/+A+5DI5Jr8wGbO6zoKjnfX9ISMLoNEA9++XXQhKm+7fr9xr2doC3t5PT+WVBjc3wMbGmO/YYrFYEJkZIQR6reqF3dd3AwBa+bXC0gFL0aZmG4mTEf3Pwx0XnzWS8OQmCI3G8NeSybQjBaUVhbImNzeT2BfBUrFYEJkZmUyGPg364Pjt4/i82+eY0HYCbOX8X5mqkBCASqUdQUhP1/4s7/eMjKcPf6woV9fyS0GNGvq3PTw4kmBieIIsIhMnhMDGyxvh4+SDznU6A9Be8yMjLwP+Lv4SpyOz9LAoVKQkpKdrRxQqUxTs7fWLwJOloLRNEQqF8d8vGQVPkEVkIb4/9T0mbp+IRl6NcP7d81DaKmErt2WpoEeE0J7/oCIl4eHvlTkU0skJ8PHRFoSH0+O3n7zPCndcJBYLIpM3MnQk5h2Zh+FNh0sdharTgwfaIpCW9ujnw98fTo9veqhMUXB2Lr0QlFUWHByM/z7J4rBYEJmQh5s9Yv6MweqXV0Mmk8HN3g1/TvwTSlul1PHoeTzcobG0olDa7yqV4a/h4lLx0QQWBaoiLBZEJuJ82nm8v+N97L+5HwAQGRyJIU2HAABLhanSaLRHM1SkKKSna0chDGFnB/j6akuBr++j6fGi8HhhsLevmvdJZAAWCyKJZeZn4p97/4klp5dAIzSwt7XH1I5T0a9RP6mjWaeSEm0JSE19dlm4exdQqw17ficn/ZLweGl48nd3dx4WSWaHxYJIImqNGktPL8Wnez/FvYJ7AIAhIUMwr8c8BLkHSZzOwjzcuTE1VX9KSXl6XkaGdnlDeHo+uyQ8/OnEi8GRZWOxIJLA3sS9iIqNwvm08wCAUJ9Q/LvPv9GlThdpg5mboiLtyEFpBeHJeYZshpDLtZsW/PyeXRhq1OAhkkSPYbEgqkbxGfH4x+5/YGvCVgCAh70HZnedjXFtxvEkVw8Job3+Q1kjCo/Pu3fPsOd2ddWWBX9/7c8np4fzvb150iWiSuJfMqJqIITA+zvex/envodaqGErt8W41uMwq8sseDl6SR2vegihvbZDcnL5U0qKYYdO2to+XQxKKwu+vjyvAlE1YLEgqgYymQxqoYZaqBERHIEvX/oSjb0bSx3LOB4eRvmswpCcDBQWVvx5PT0rNrrg4aHddEFEJoGn9CaqAmqNGqvOr0Kbmm3Q1KcpAO0lzv+8+yc6BXWSOJ0B8vL0RxLKKgyGXIra0xOoWbPsyd9fO7qg5CG2RKaEp/QmktDU3VPx9dGv0adBH2wfuR0A4OPkAx8nH4mT/Y9Goz1U8vZt4M4d7c+H05072ik52bCTNLm5lV8WHv7kuRaILBqLBZGRFKuLYWdjBwAY12Ycos9Fo2udrtAIDeSyahyqLynR7tj4eFEorThU9KJSTk5ArVqlF4XHb/MwSiICiwXRczuXeg6f/PEJPB088UvkLwCABp4NcOvvt2Bva+R/nT94oB1JeLIoPH47NVU7IvEsMpl2k0NAwKOpVi3tFBDwqDS4uBj3PRCRRWOxIKqkhMwEzNg3A2svrgUA2Mnt8FWPr+Dn7AcAhpcKtVq7H8OtW0BSkvbn49Pt29rNFxVha6stBU+Whsdv+/trTxlNRGRELBZEBkrKTsJn+z/D8rjlUAvt6ZyHNxuOz7p8pisVpcrOfrosPF4g7tzRbsZ4Fnt7/YJQWmnw8eGREkQkCRYLogpKzknGV4e/wpJTS1Co1h422b9Rf3ze9XO08GyiLQaXDpRdHiqyI6StrbYYBAYCtWs/mgIDtVNAgPbwSl4/gohMFIsF0TPcVt3Gl/u/wE9xy1Co0e7w2FlTG/+6E4wOu7KAj/pp93uoyJHbXl5PF4bHb/v58YyPRGTWWCyIAO0REklJwI0buinp9iXMsTmKn2umouh/3/V/uwnM2A+8dP0WZLil/xxKZell4eEUEMAjJ4jI4rFYkHUoLn6qOOimxETtZownRhwS6gLfj9b+3vkGMOOoAl1s6kMWXBfoXQeo878pKEj7s0YNbqIgIqvHYkGWIycHuHZNf7p+Xfvz1i3tURfluOanwIWmNRChaA7UqYNuQUH4u+NBDGrQH53Hv8ziQERUASwWZD6E0B6O+XhheHx61qGYSuWjUYa6dR/9XqcOzjip0Pa33nCyU+FG1Cp4OnhCBmABPq7yt0VEZElYLMi0lJQAN28CCQlPjzpcvw4UFJT/eG9voH597VSv3qPf69fX7hj5v0MwhRC4lX0LQe5BAIBWQqDpwaao5VoL2Q+y4engWdXvlIjIIrFYUPV7OPKQkKCdrl599Pu1a+VfMlsu1+7T8GRpeHj7GRe2U2vU2BS/CV8d/go37t/AzaibcFI4QSaT4chbR+CscDbymyUisi4sFlR1srIeFYYnS0R5V8NUKoEGDYCGDZ8eeQgKqtTZIguKCxB9LhpfH/ka17KuAQAcbB1wKvkUOtfpDAAsFURERsBiQc9HrdZuooiPfzQ9LBDl7fNgY6Pdz6FhQ6BRI/0pIMBoZ41MzknGdye/ww+nf8DdfG0eTwdPvNfuPUxqNwnejt5GeR0iItJisaCKKSzUFob4eODyZf0SUVhY9uNq1XpUGB4vEXXrAgpFlcU9cecEFh1fhPWX1qNEoz1Ndm232vgw/EO81eotOCl4PgkioqrAYkH6cnL0Rx8eFonr18u+YqaDA9C4MdCkiXZq3FhbHho0AJyrb/NCsboYm+I3YdHxRTh2+5hu/t9q/w1R7aMwKHgQbOX8yBMRVSX+lbVWxcXa0YYLF/SnGzfKfoy7+6Py0KQJEBKi/RkUZBIXvFp1fhXe3PImAEBho8DwZsPxQfsPEOYfJnEyIiLrwWJh6YTQnlXyyQIRH689jXVp/PwelYbHJz8/kzlBlBACR5KOIK84Dz3r9wQADGs2DPOOzMPQpkPxbpt3y7/SKBERVQkWC0tSVKTdbHH2LHDmDHDuHHDxovbojNK4uADNmgGhofqTp+mfw2HV+VV4ffPraOLdBJcmXIJMJoOjnaPudyIikgaLhbnKywPOn9eWiIdF4uLF0kchbGy0+z2EhgLNmz8qEEFBJjMCUR4hBE4mn0RBcYHu0NCBjQeihmMNhAeEI784X7czJksFEZG0WCzMQX6+tjicOKH9eeYMcOVK6TtTursDrVppp5YttUUiOFh7bggzc//Bfay9uBZLTy/F2dSzCPMPw+l3TgMA3OzdcHvybShsqu7IEiIiMhyLhanRaLT7P5w4ARw/rp0uXCj9Alr+/o9KRFiY9medOmYxClEWtUaNXdd3YUXcCmz+czMK1dpDWZU2SjSt0RQFxQVwsHMAAJYKIiITxGIhteTkRyXixAng5EntIZ9P8vcH2rcH2rR5VCL8LGfnxPiMeESfi8bK8yuRnJOsm9/MpxnGtByD0S1Gw8vRS8KERERUESwW1UkI7SGeBw8+mhITn17O0VFbINq3107t2mnPRmnGIxGlySrIwtqLaxF9LhrH7xzXzfd08MTI0JF4o+UbaOXXivtNEBGZERaLqqRWa4/MOHgQOHAAOHQISE/XX0YmA5o2fVQi2rfXHuppa9n/aYQQaLGkBZJUSQAAG5kN+jbsizdavoF+DftBaWt++4QQERGLhXEJoT3cc/du7bR//9ObNZRK7QjEiy9qpw4dnnlFTnNXrC7GtqvbsOPqDnzf/3vIZXLIZDIMbDwQB24ewJiWY/Bq6KvwdfaVOioRET0nmRBCVOcLqlQquLm5ITs7G66W8IV65w6wZw+wa5e2TKSm6t/v6gp07PioSLRta5ZHaDyPwpJC+H7ti+zCbOx/Yz86BXXSzefIBBGReajo9zdHLAyl0Wh3sNy6VTvFxenfb28PdOoEdO8OvPQS0KKF9jwSVqCguAC7ru9CzJ8xiM+Ix9G3jkImk0Fpq8T4NuNRrClGLZdauuVZKoiILA+LRUXk5mpHJP7v/4Bt2/T3k5DJtDta9uihLRPh4dpyYSWyCrKwNWErNl/ZjJ1/7UR+cb7uvtMpp9GmZhsAwJzuc6SKSERE1YjFoiy5udoRiXXrgB079C8N7uIC9O4NDBgA9OkDeHtLl1MCt1W38fufvyPmzxjsv7lfd1lyAAhyC0JEcAQigyPR0q+ldCGJiEgSLBaPKy7WjkisXq39WVDw6L569bRFYsAA7b4SCus5OZMQAvtv7seOqzuw468duJB+Qe/+UJ9QvTLBw0OJiKwXiwWgPZJj+XLgl1/0N3PUrw8MGwYMHao9NbYVfWHeK7gHTwftxchkMhkmbJuA+Lvx2tuQoUNgB0QGR2JQ8CA08GwgZVQiIjIh1lssSkqAmBjgm2+Ao0cfzff1BUaNAkaM0J7d0orKBACk56WjW3Q3JN5PROY/MmFvq91fZGToSFzJvII+DfqgZ/2ePAsmERGVyvqKRW6udnTim28enfXSxgbo3x94803tPhN2dtJmrAb5xfk4fOsw9t7YC1u5LT7r+hkAoIZjDWQ9yMKDkgeIS43DCwEvAAA+6fSJlHGJiMhMWE+xyM0FFiwAFi4EsrK087y8gEmTgHfftajrbpQmvzgfJ+6cwN7Evdh7Yy+O3T6GYk0xAG2ZmNVlFmQyGWQyGWKGxaCBZwPdphAiIqKKsvxiodEAP/4IzJgBpKVp5zVoAEyeDIwerb0uh4URQuBm9k0cTTqKI0lHcPT2UcSlxkEt9K+QGugaiK51u6Jrna4o0ZTAzkY7UtOuVjspYhMRkQWw7GJx+TIwduyjfSgaNAA+/xx45RWLOmmVEEJ3JMbJOycxaO0gpOSmPLVcLZda6BTUCd3qdkPXOl1Rz6Mej+AgIiKjstxi8fPPwIQJQFER4OwMfPEFMH68Re0/8fOZn7Hg2AK80uQVzOo6CwAQ5B6ElNwU2Mpt0cqvFToEdkB4QDg6BHZAoFugxImJiMjSWV6xUKuBjz8G5s/X3u7bF1iyBAg0ry9VjdDgxv0buJxxGRfTL+Js6lmcSTmD9a+sRyv/VgCAInURLmdcxkm3k7rH+Tj54Nhbx9Dctzkc7Bykik9ERFbK8orFJ588KhUzZmgnEx7uV2vUuJ51HZczLuNyxmVcyriEyxmX8efdP1FQUvDU8mdSzuiKRf9G/RHkHoQw/zC9ZdoHtK+W7ERERE+qVLFYvHgx5s2bh9TUVLRo0QLffvst2rUzgR3+UlOBRYu0vy9bBowZI22e/yksKcRf9/5CfnE+2tZqq5vf7sd2OJ92HoXqwlIfp7RRItg7GE1qNEErv1YI8w/TXXsDAALdArl5g4iITIrBxWLdunWYPHkylixZgvbt22PhwoXo1asXrly5Ah8fn6rIWHHz5gEPHgAvvAC88Ua1vGRhSSFSclNwR3UHd3Lu6H72b9QfXep0AQDsvbEXfVb3QahPKM6PP//osepCFKoL4WDrgCY1miCkRghCvEO0P2uEoJ5HPdjILWcnUyIisnwGF4sFCxbg7bffxpj/jQYsWbIE27Ztw7JlyzB16lSjB6yw9HTg+++1v1dy84dao8b9B/dRpC6Cv4u/bn50XDSuZ11HZkEm7ubfRWZBJjLyMnAn5w7u5t8t9bnclG66YlHfoz7clG5wt3fXW2Zl5Eq4KFwQ5B4EuUxucF4iIiJTY1CxKCoqwunTpzFt2jTdPLlcju7du+Po46fFfkxhYSEKH7syqEqlqmTUZ/j6a8xqV4C0ej4oKd6Ekt/XQy3UKNGU6E2FJYXIK85DblEu8ory8FGHj/B267cBAMfvHEfHZR3R0LMhEt5L0D31wuMLEZcaV+ZLK22UqOlSE7Vca6GWi3YKDwzX3d/AswGyPs566tDO5r7NjbsOiIiIJGZQsbh79y7UajV8fX315vv6+uLPP/8s9TFz5szBrFmzKp+wYsGAxYux6i3gL6904MxPFX5oWl6a7ndnhTMA7VkqH/dy8MsIDwiHl4MXvBy94OXgBW9Hb12R8HTwLPd8EDxXBBERWYsqPypk2rRpmDx5su62SqVCoLEP/fT0BH75BZP2fYn7nfvBRm4L2zImO7kdnBXOcFI4wVnhjLrudXVP08ynGYqnF8NWrr9apneebty8REREFsqgYuHt7Q0bGxukpaXpzU9LS4NfGdfaUCqVUCqVlU9YEXI5MHgwPhg8+PmeRibnvg5ERETPwaBvUYVCgdatW2PPnj26eRqNBnv27EF4eHg5jyQiIiJrYPCmkMmTJ2P06NFo06YN2rVrh4ULFyIvL093lAgRERFZL4OLxbBhw5CRkYF//vOfSE1NRcuWLbFz586ndugkIiIi6yMTQojqfEGVSgU3NzdkZ2fD1dW1Ol+aiIiIKqmi39/cU5GIiIiMhsWCiIiIjIbFgoiIiIyGxYKIiIiMhsWCiIiIjIbFgoiIiIyGxYKIiIiMhsWCiIiIjIbFgoiIiIymyi+b/qSHJ/pUqVTV/dJERERUSQ+/t591wu5qLxY5OTkAgMDAwOp+aSIiInpOOTk5cHNzK/P+ar9WiEajQXJyMlxcXCCTyYz2vCqVCoGBgUhKSuI1SJ6B66riuK4Mw/VVcVxXFcd1VXFVua6EEMjJyUHNmjUhl5e9J0W1j1jI5XIEBARU2fO7urryg1dBXFcVx3VlGK6viuO6qjiuq4qrqnVV3kjFQ9x5k4iIiIyGxYKIiIiMxmKKhVKpxIwZM6BUKqWOYvK4riqO68owXF8Vx3VVcVxXFWcK66rad94kIiIiy2UxIxZEREQkPRYLIiIiMhoWCyIiIjIaFgsiIiIyGrMqFosXL0adOnVgb2+P9u3b48SJE+Uuv2HDBgQHB8Pe3h6hoaHYvn17NSWVniHrasWKFZDJZHqTvb19NaaVzoEDBzBgwADUrFkTMpkMmzdvfuZj9u3bh7CwMCiVSjRo0AArVqyo8pymwNB1tW/fvqc+VzKZDKmpqdUTWEJz5sxB27Zt4eLiAh8fH0RERODKlSvPfJw1/s2qzLqy1r9Z33//PZo3b647+VV4eDh27NhR7mOk+EyZTbFYt24dJk+ejBkzZuDMmTNo0aIFevXqhfT09FKXP3LkCEaMGIG33noLZ8+eRUREBCIiInDx4sVqTl79DF1XgPYsbSkpKbrp5s2b1ZhYOnl5eWjRogUWL15coeUTExPRr18/dO3aFXFxcYiKisLYsWMRGxtbxUmlZ+i6eujKlSt6ny0fH58qSmg69u/fj4kTJ+LYsWPYtWsXiouL0bNnT+Tl5ZX5GGv9m1WZdQVY59+sgIAAfPnllzh9+jROnTqFbt26YdCgQbh06VKpy0v2mRJmol27dmLixIm622q1WtSsWVPMmTOn1OWHDh0q+vXrpzevffv2Yty4cVWa0xQYuq6WL18u3Nzcqimd6QIgYmJiyl3mH//4h2jatKnevGHDholevXpVYTLTU5F1tXfvXgFAZGVlVUsmU5aeni4AiP3795e5jDX/zXpcRdYV/2Y94uHhIX766adS75PqM2UWIxZFRUU4ffo0unfvrpsnl8vRvXt3HD16tNTHHD16VG95AOjVq1eZy1uKyqwrAMjNzUVQUBACAwPLbcDWzlo/V8+jZcuW8Pf3R48ePXD48GGp40giOzsbAODp6VnmMvxsaVVkXQH8m6VWq7F27Vrk5eUhPDy81GWk+kyZRbG4e/cu1Go1fH199eb7+vqWub02NTXVoOUtRWXWVePGjbFs2TL8/vvvWLVqFTQaDTp06IDbt29XR2SzUtbnSqVSoaCgQKJUpsnf3x9LlizBpk2bsGnTJgQGBqJLly44c+aM1NGqlUajQVRUFDp27IhmzZqVuZy1/s16XEXXlTX/zbpw4QKcnZ2hVCrx7rvvIiYmBiEhIaUuK9VnqtqvbkqmJzw8XK/xdujQAU2aNMEPP/yA2bNnS5iMzFnjxo3RuHFj3e0OHTrg2rVr+Oabb7By5UoJk1WviRMn4uLFizh06JDUUUxeRdeVNf/Naty4MeLi4pCdnY2NGzdi9OjR2L9/f5nlQgpmMWLh7e0NGxsbpKWl6c1PS0uDn59fqY/x8/MzaHlLUZl19SQ7Ozu0atUKf/31V1VENGtlfa5cXV3h4OAgUSrz0a5dO6v6XE2aNAlbt27F3r17ERAQUO6y1vo36yFD1tWTrOlvlkKhQIMGDdC6dWvMmTMHLVq0wKJFi0pdVqrPlFkUC4VCgdatW2PPnj26eRqNBnv27Clz21J4eLje8gCwa9euMpe3FJVZV09Sq9W4cOEC/P39qyqm2bLWz5WxxMXFWcXnSgiBSZMmISYmBn/88Qfq1q37zMdY62erMuvqSdb8N0uj0aCwsLDU+yT7TFXprqFGtHbtWqFUKsWKFSvE5cuXxTvvvCPc3d1FamqqEEKIUaNGialTp+qWP3z4sLC1tRVff/21iI+PFzNmzBB2dnbiwoULUr2FamPoupo1a5aIjY0V165dE6dPnxbDhw8X9vb24tKlS1K9hWqTk5Mjzp49K86ePSsAiAULFoizZ8+KmzdvCiGEmDp1qhg1apRu+evXrwtHR0fx0Ucfifj4eLF48WJhY2Mjdu7cKdVbqDaGrqtvvvlGbN68WVy9elVcuHBBfPDBB0Iul4vdu3dL9Raqzfjx44Wbm5vYt2+fSElJ0U35+fm6Zfg3S6sy68pa/2ZNnTpV7N+/XyQmJorz58+LqVOnCplMJv773/8KIUznM2U2xUIIIb799ltRu3ZtoVAoRLt27cSxY8d093Xu3FmMHj1ab/n169eLRo0aCYVCIZo2bSq2bdtWzYmlY8i6ioqK0i3r6+sr+vbtK86cOSNB6ur38JDIJ6eH62f06NGic+fOTz2mZcuWQqFQiHr16only5dXe24pGLqu5s6dK+rXry/s7e2Fp6en6NKli/jjjz+kCV/NSltPAPQ+K/ybpVWZdWWtf7PefPNNERQUJBQKhahRo4Z46aWXdKVCCNP5TPGy6URERGQ0ZrGPBREREZkHFgsiIiIyGhYLIiIiMhoWCyIiIjIaFgsiIiIyGhYLIiIiMhoWCyIiIjIaFgsiIiIyGhYLIiIiMhoWCyIiIjIaFgsiIiIyGhYLIiIiMpr/BwXkER7AtRm7AAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"xt = np.linspace(0, 3, num=200)\n",
|
||
"sqrt = np.sqrt(xt)\n",
|
||
"square = np.square(xt)\n",
|
||
"\n",
|
||
"plt.plot(xt, sqrt, color='r', label=\"Square Root\")\n",
|
||
"plt.plot(xt, square, color='g', label=\"Square Function\", linestyle=\"dashdot\")\n",
|
||
"plt.legend()\n",
|
||
"plt.show()\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "d33d372a-ed48-4a31-a1fc-4b325e910d27",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-6d0019ce99d7aacb",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "7dd33f6a-1e5d-4c8f-8778-7820d13fa357",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-c7e6f6e837a94d41",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Warum Zufall?\n",
|
||
"\n",
|
||
"Für statistische Analysen jeglicher Art ist es wichtig, die verwendeten Werkzeuge gut zu verstehen. Da nicht immer direkt ein vollständiges Dataset vorliegt oder dieses sich noch im Erstellungsprozess befindet, bietet es sich an, die mathematischen und programmatischen Methoden zunächst an nachvollziehbaren Zufallsdaten zu testen. \n",
|
||
"\n",
|
||
"In dieser Übung wollen wir daher lernen, was Zufall bedeutet, wie Zufallsgeneratoren funktionieren und auf welche Weise Zufallszahlen gezielt erzeugt oder manipuliert werden können, um verschiedene Szenarien realistisch zu simulieren.\n",
|
||
"\n",
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "6536feb0-7612-4bad-b797-3960ed3c832c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-f387eeef09033ea3",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Was ist Zufall?\n",
|
||
"\n",
|
||
"Für Zufall existieren viele unterschiedliche Definitionen. Doch was genau ist Zufall eigentlich? Das Würfeln eines Würfels zum Beispiel ist streng genommen nicht zufällig. Jeder einzelne Würfelwurf kann theoretisch vorhergesagt werden, vorausgesetzt, alle erforderlichen Daten wie Kraft, Winkel, Untergrund und Luftwiderstand sind bekannt. Auch das Wetter ist in diesem Sinne nicht zufällig. Alle Ereignisse lassen sich prinzipiell vorhersagen, wenn genügend Daten vorhanden sind – das eigentliche Problem besteht lediglich darin, dass es in der Praxis niemals ausreichend Daten gibt. \n",
|
||
"\n",
|
||
"Nahezu jedes weitere Beispiel kann mit derselben Argumentation als „zufällig“ widerlegt werden. Daher werden solche Phänomene als *pseudo-zufällig* bezeichnet, da sie zwar unvorhersehbar erscheinen, aber einem deterministischen System folgen. \n",
|
||
"\n",
|
||
"Doch das nur am Rande. In der Physik existiert ein Phänomen, das als wirklich unvorhersehbar gilt. Wird ein einzelnes Photon auf einen halbtransparenten Spiegel geschossen, kann __nie__ vorhergesagt werden, auf welchen der beiden Detektoren das Photon treffen wird. Diese Form des echten Zufalls wird von der Firma [ID Quantique](https://www.idquantique.com/random-number-generation/overview/) genutzt, die Geräte entwickelt und vertreibt, welche genau dieses Quantenphänomen zur Erzeugung echter Zufallszahlen verwenden. \n",
|
||
"\n",
|
||
"Doch genug von echter Koinzidenz – zurück zum Pseudo-Zufall und der Frage, wie Computer mit diesem scheinbaren Zufall umgehen und ihn für Simulationen und statistische Zwecke nutzbar machen.\n",
|
||
"\n",
|
||
"---"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "73c86ab1-9f06-4dc5-861b-6558e8315bb3",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-fde25777024719e0",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"# Pseudo Randomness\n",
|
||
"\n",
|
||
"Zufallszahlen in Computern werden nicht wirklich zufällig erzeugt, sondern über mathematische Formeln berechnet. Einer der bekanntesten Generatoren ist der _Linear Congruent Generator (LCG)_, dessen mathematische Grundlage leicht verständlich ist:\n",
|
||
"\n",
|
||
"$$ X_{n+1} = (aX_n + c) \\;\\text{mod}\\; m, \\quad n \\geq 0 $$\n",
|
||
"\n",
|
||
"Wenn $c = 0$ gilt, spricht man auch vom _Multiplicative Congruent Generator (MCG)_. \n",
|
||
"\n",
|
||
"Die einzelnen Werte haben folgende Bedeutung: \n",
|
||
"\n",
|
||
"- $X_n$ ist der Startwert, auch **Seed** genannt. \n",
|
||
"- $X_{n+1}$ ist der Folgewert, der im nächsten Schritt als $X_n$ verwendet wird. \n",
|
||
"- $a$ ist der Vorfaktor des Startwerts, wird auch als **Skalar** bezeichnet, da er den Wert skaliert. \n",
|
||
"- $c$ ist das hinzuaddierte **Offset**. \n",
|
||
"- $m$ ist der Restklassenring oder **Modulus**, der die Werte in einem festen Bereich hält.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "39b18b10-a831-4fbe-a50b-d8177108bca1",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-a1c6ad2b24a97f6b",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe\n",
|
||
"\n",
|
||
"*6 Punkte*\n",
|
||
"\n",
|
||
"Schreibe einen _Linear Congruent Generator_ mit dem Funktionsnamen `lcg`.\n",
|
||
"\n",
|
||
"- Verwende die oben gegebene mathematische Definition: \n",
|
||
" $$ X_{n+1} = (aX_n + c) \\;\\text{mod}\\; m, \\quad n \\geq 0 $$\n",
|
||
"- Prüfe, dass die Eingabewerte gültig sind. \n",
|
||
"- `lcg` soll als **unendlicher Generator** implementiert werden, der bei jedem Aufruf den nächsten Wert der Pseudo-Zufallsfolge liefert.\n",
|
||
"- Ekläre in der Markdownzeile die Funktionsweise des Generators. (Keine Erklärung = 0 Punkte)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 39,
|
||
"id": "224134b7-6ab5-4438-ad46-6cb77261680c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-d5c7ad13eb813b34",
|
||
"locked": false,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"def lcg(seed: int, scalar: int, modulus: int, offset: int) -> int:\n",
|
||
" ''' \n",
|
||
" Linear Congruential Generators\n",
|
||
"\n",
|
||
" X(n+1) = (a X(n) + c) mod m; n >= 0\n",
|
||
"\n",
|
||
" m > 0; \n",
|
||
" 0 <= a < m;\n",
|
||
" c > 0; a > 0\n",
|
||
"\n",
|
||
" '''\n",
|
||
" assert modulus > 0, \"Modulus must be greater than 0\"\n",
|
||
" assert 0 <= scalar and scalar < modulus, \"Scalar must be in range 0 <= a < m\"\n",
|
||
"\n",
|
||
" while seed > 1:\n",
|
||
" seed = (scalar*seed+offset) % modulus\n",
|
||
" assert seed >= 0\n",
|
||
" yield seed\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "ef57bf76-127c-4987-be25-126d60453cb9",
|
||
"metadata": {},
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 90,
|
||
"id": "853a70eb-7dd1-43b5-af99-ed1b3126846c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-35fbf31fbee439df",
|
||
"locked": true,
|
||
"points": 6,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"Lcg using Cocktailshaker Numbers: 3089810780120156248\n",
|
||
"Correct should be: 3089810780120156248\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 8356396685252565260\n",
|
||
"Correct should be: 8356396685252565260\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 1921117399837525548\n",
|
||
"Correct should be: 1921117399837525548\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 14806858147081821235\n",
|
||
"Correct should be: 14806858147081821235\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 2557599628047639428\n",
|
||
"Correct should be: 2557599628047639428\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 16453652254840064460\n",
|
||
"Correct should be: 16453652254840064460\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 15995401842808378843\n",
|
||
"Correct should be: 15995401842808378843\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 681272290641816305\n",
|
||
"Correct should be: 681272290641816305\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 10955466795170118648\n",
|
||
"Correct should be: 10955466795170118648\n",
|
||
"\n",
|
||
"Lcg using Cocktailshaker Numbers: 13714992071537968180\n",
|
||
"Correct should be: 13714992071537968180\n",
|
||
"\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"# Hier werden ihre Lösungen getestet ...\n",
|
||
"\n",
|
||
"# Check if lcg is a properly defined\n",
|
||
"assert 'lcg' in dir()\n",
|
||
"\n",
|
||
"# Check if lcg is a generator\n",
|
||
"import types\n",
|
||
"assert isinstance(lcg(1,1,1,1), types.GeneratorType) # 1 Punkt\n",
|
||
"\n",
|
||
"# Using Cocktailshaker numbers :)\n",
|
||
"s = lcg(3935559000370003845, 3203021881815356449, 2**64-1, 11742185885288659963)\n",
|
||
"### BEGIN HIDDEN TESTS\n",
|
||
"def lcg_test(seed: int, scalar: int, modulus: int, offset: int) -> int:\n",
|
||
" assert modulus > 0, \"Modulus must be greater than 0\"\n",
|
||
" assert 0 <= scalar and scalar < modulus, \"Scalar must be in range 0 <= a < m\"\n",
|
||
"\n",
|
||
" while seed > 1:\n",
|
||
" seed = (scalar*seed+offset) % modulus\n",
|
||
" assert seed >= 0\n",
|
||
" yield seed\n",
|
||
"\n",
|
||
"t = lcg_test(3935559000370003845, 3203021881815356449, 2**64-1, 11742185885288659963)\n",
|
||
"### END HIDDEN TESTS\n",
|
||
"\n",
|
||
"# Check if Generator works\n",
|
||
"for _ in range(10):\n",
|
||
" stud = next(s)\n",
|
||
" instructor = next(t)\n",
|
||
" print(\"Lcg using Cocktailshaker Numbers:\", stud)\n",
|
||
" print(\"Correct should be:\", instructor, end='\\n\\n')\n",
|
||
" assert stud == instructor\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 95,
|
||
"id": "a8ec682f-79eb-463f-86eb-a063639d040b",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"1. 3089810780120156248\n",
|
||
"2. 8356396685252565260\n",
|
||
"3. 1921117399837525548\n",
|
||
"4. 14806858147081821235\n",
|
||
"5. 2557599628047639428\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"rand = lcg(\n",
|
||
" 3_935_559_000_370_003_845,\n",
|
||
" 3_203_021_881_815_356_449,\n",
|
||
" 2**64-1,\n",
|
||
" 11_742_185_885_288_659_963\n",
|
||
" )\n",
|
||
"\n",
|
||
"for i in range(5):\n",
|
||
" print(f\"{i+1}. {next(rand)}\")"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "8e516bd4-c203-4b11-9880-31eabba13c2e",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-88eadd4386332f26",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"---\n",
|
||
"\n",
|
||
"# A Family of Better Random Number Generators\n",
|
||
"\n",
|
||
"<div style=\"display: flex; justify-content: center;\">\n",
|
||
" <figure style=\"margin-top: 30px;\">\n",
|
||
" <img src=\"https://www.cs.hmc.edu/~oneill/images/melissa1.jpg\" width=\"300\">\n",
|
||
" <figcaption>\n",
|
||
" <p style=\"text-align:center; font-size: 20px;\">\n",
|
||
" <strong>Melissa E. O’Neill</strong>\n",
|
||
" </p>\n",
|
||
" </figcaption>\n",
|
||
" </figure>\n",
|
||
" <div style=\"margin-left: 40px; max-width: 60%; word-wrap:break-word;\">\n",
|
||
" <br/>\n",
|
||
" <p><i>Linear Congruent Generators</i> zeichnen sich durch ihre Stabilität und Geschwindigkeit als Hervorragende Zufallsgeneratoren. Doch 2014 gelang Melissa E. O'Neil ein neuer Durchbruch in der Konzeption von Pseudozufallsgeneratoren. Das Problem mit existierenden Zufallsgeneratoren ist entweder ihre Stabilität (Wie vorhersehbar die Zufallszahlen sind) oder ihre Geschwindigkeit (Wie lange der Zufallsgenerator braucht um die nächste Zufallszahl zu errechnen).</p>\n",
|
||
" <p>Ihr Durchbruch gelang, indem Sie die Vorteile eines <i>Linear Congruent Generators</i> mit dem eines <i>XorShift Generators</i> verband. Dadurch erreichte Sie nicht nur eine Normalverteilung in den generierten Zufallszahlen (und eine damit einhergende Stabilität), Sie hatte auch eine Family von schnellen einfachen Algorithmen entwickelt. Diese nennen sich <i>PCG - Permuted Congruential Generator</i>.</p>\n",
|
||
" <p>Die Implementierungsdetails lassen wir im nächsten Schritt aus, da diese nicht einfach in Python umzusetzen sind. Auf der Webseite <a href=\"https://www.pcg-random.org\" >pcg-random.org</a> lassen sich Implemtierungen für C & C++ finden. Als weiterführende Literatur ist <a href=\"https://www.pcg-random.org/pdf/hmc-cs-2014-0905.pdf\" >PCG: A Family of Simple Fast Space-Efficient Statistically Good Algorithms for Random Number Generation - Melissa E. O’Neill</a> angegeben.</p>\n",
|
||
" </div>\n",
|
||
"</div>\n",
|
||
"\n",
|
||
"Zum Glück hat _Numpy_ eine Implementierung des _PCG_. Diese findet sich unter [Numpy PCG64](https://numpy.org/doc/stable/reference/random/index.html)."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "81959fe2-2f2f-4f57-9360-4e96dc0674ba",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3cfb52b705a8d147",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe\n",
|
||
"\n",
|
||
"*6 Punkte*\n",
|
||
"\n",
|
||
"Plotte die Zufallszahlen eines _Permuted Congruent Generators_ (PCG) mithilfe von NumPy und Matplotlib.\n",
|
||
"\n",
|
||
"- Gegeben ist der Anfangszustand des Generators. \n",
|
||
"- Verwende die NumPy-Dokumentation um **20** Zufallszahlen zu erzeugen und speichere sie in der Variablen `pcgs` (Tipp: als NumPy Array). \n",
|
||
"- Sortiere anschließend die Werte in `pcgs` und speichere das Ergebnis in `pcgs_sorted`. \n",
|
||
"- Plotte sowohl die ursprünglichen als auch die sortierten Zufallszahlen in einem sinnvollen Diagramm (z. B. Linienplot oder Scatterplot) und gestalte den Plot übersichtlich.\n",
|
||
"- Erkläre in der gegebenen Markdown Zeile deinen Plot. (Keine Erklärung = 0 Punkte)\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 96,
|
||
"id": "a2fbf6d5-9460-48bc-8183-b2afb9c5c186",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-9e88f0a0a4a77c47",
|
||
"locked": false,
|
||
"points": 3,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiMAAAGzCAYAAAD9pBdvAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAXTtJREFUeJzt3XlcVNX/P/DXMOy7CiKb4L6LioobqYVrbuGC+5JpmZpmfn8uH5cyi9Iy1zQttXItQy0zTQnKEkVFc98BEQEBZREEZOb8/phmdGRH4M7yej4e8zDunHvnfecyzYtzzz1XJoQQICIiIpKIidQFEBERkXFjGCEiIiJJMYwQERGRpBhGiIiISFIMI0RERCQphhEiIiKSFMMIERERSYphhIiIiCTFMEJERESSYhghohfm7e2N8ePHS12GXnj//fchk8mQkpIidSlEOoNhhOgZW7duhUwm0zwsLS3RsGFDTJs2DUlJSQXaJyUlYfbs2WjcuDGsra1hY2MDX19fLF26FGlpaQXa//LLL+jfvz9cXFxgbm6O6tWr46WXXsLnn3+OjIyMEusbP368Vn0WFhZo2LAhFi1ahJycnIp4CwyC+n1q2bIlCrvjhUwmw7Rp0ySojIgKYyp1AUS6aMmSJahTpw5ycnLw999/Y/369Th48CAuXrwIa2trAMCpU6fQt29fPHr0CKNHj4avry8A4PTp0/jkk0/w119/4ffffwcAKJVKTJw4EVu3bkWLFi3w9ttvw9PTE5mZmYiIiMCCBQtw8OBBhIaGllibhYUFvv76awBAeno69u/fjw8//BC3bt3C9u3bK+kd0U8XLlxASEgIBg8eLHUpRFQMhhGiQvTp0wdt27YFALzxxhuoUaMGVqxYgf3792PEiBFIS0vDa6+9BrlcjrNnz6Jx48Za63/00UfYtGmT5udly5Zh69atePfdd/H5559DJpNpnpsxYwYSEhLw3Xfflao2U1NTjB49WvPz22+/jU6dOmHnzp1YsWIFXFxcXmTXDYaVlRU8PT2xZMkSBAYGar3nxiA7O1sTnIl0HU/TEJXCyy+/DACIjo4GAHz11VeIj4/HihUrCgQRAHBxccGCBQsAqL4UPv30UzRr1gzLly8v9EvR1dUVc+bMKVdtMpkMXbp0gRACt2/f1iyPjY3F22+/jUaNGsHKygo1atTA0KFDERMTo7W++tTUP//8g1mzZsHZ2Rk2NjZ47bXXkJycrNVWCIGlS5fCw8MD1tbW6N69Oy5dulRoXbdv38bQoUNRvXp1WFtbo0OHDvj111+12oSHh0Mmk+GHH37ABx98AHd3d9jZ2WHIkCFIT09Hbm4uZs6ciZo1a8LW1hYTJkxAbm5uqd4XExMTLFiwAOfPn8fevXuLbat+D55/b9T1hYeHa5Z169YNzZs3x/nz59G1a1dYW1ujfv362LNnDwDgzz//hJ+fH6ysrNCoUSMcPXq00NdMSUnBsGHDYG9vjxo1amDGjBmFnmrbtm0bfH19YWVlherVq2P48OGIi4vTaqOu6cyZM3jppZdgbW2N+fPnA1D11PXq1QtOTk6wsrJCnTp18Prrr5f09hFVKYYRolK4desWAKBGjRoAgJ9//hlWVlYYMmRIiev+/fffSEtLw4gRIyCXyyulPvWXaLVq1TTLTp06hePHj2P48OFYvXo13nrrLYSGhqJbt27Izs4usI3p06fj33//xeLFizFlyhT88ssvBcZVLFq0CAsXLoSPjw+WL1+OunXromfPnsjKytJql5SUhE6dOuHw4cN4++238dFHHyEnJwcDBgwoNBgEBwfj8OHDmDt3Ll5//XWEhITgrbfewuuvv47r16/j/fffR2BgILZu3YpPP/201O/LyJEj0aBBAyxZsqTQsSPl9fDhQ/Tr1w9+fn5YtmwZLCwsMHz4cOzevRvDhw9H37598cknnyArKwtDhgxBZmZmgW0MGzYMOTk5CA4ORt++fbF69WpMnjxZq81HH32EsWPHokGDBlixYgVmzpyJ0NBQvPTSSwXGJKWmpqJPnz5o1aoVVq5cie7du+P+/fvo2bMnYmJiMHfuXKxZswajRo3CiRMnKuy9IKoQgog0tmzZIgCIo0ePiuTkZBEXFyd27dolatSoIaysrMTdu3eFEEJUq1ZN+Pj4lGqbq1atEgDEvn37tJbn5+eL5ORkrYdSqSx2W+PGjRM2Njaa9jdv3hSfffaZkMlkonnz5lrrZ2dnF1g/IiJCABDfffddgX0OCAjQWv/dd98VcrlcpKWlCSGEuH//vjA3NxevvvqqVrv58+cLAGLcuHGaZTNnzhQAxLFjxzTLMjMzRZ06dYS3t7dQKBRCCCHCwsIEANG8eXORl5enaTtixAghk8lEnz59tOrv2LGj8PLyKvY9evZ9EkKIb7/9VgAQISEhmucBiKlTpxZ4D6Kjo7W2o64vLCxMs6xr164CgNixY4dm2dWrVwUAYWJiIk6cOKFZfvjwYQFAbNmyRbNs8eLFAoAYMGCA1mu9/fbbAoD4999/hRBCxMTECLlcLj766COtdhcuXBCmpqZay9U1bdiwQavt3r17BQBx6tSp4t4uIsmxZ4SoEAEBAXB2doanpyeGDx8OW1tb7N27F+7u7gCAjIwM2NnZlWpb6qtkbG1ttZZfuHABzs7OWo/U1NQSt5eVlaVpX79+fcyePRudO3fG/v37tU4BWVlZaf77yZMnSE1NRf369eHo6IioqKgC2508ebLW+v7+/lAoFIiNjQUAHD16FHl5eZg+fbpWu5kzZxbY1sGDB9G+fXt06dJFs8zW1haTJ09GTEwMLl++rNV+7NixMDMz0/zs5+cHIUSB0wl+fn6Ii4tDfn5+SW+TxqhRoyq8d8TW1hbDhw/X/NyoUSM4OjqiSZMm8PPz06oXgNbpM7WpU6dq/Tx9+nQAqvcOAEJCQqBUKjFs2DCkpKRoHrVq1UKDBg0QFhamtb6FhQUmTJigtczR0REAcODAATx58qSce0tU+RhGiAqxbt06HDlyBGFhYbh8+TJu376NXr16aZ63t7cvtOu9MOrQ8ujRI63l9evXx5EjR3DkyBGMGTOm1LVZWlpq1tuyZQuaNGmC+/fva4UPAHj8+DEWLVoET09PWFhYwMnJCc7OzkhLS0N6enqB7dauXVvrZ/Upn4cPHwKAJpQ0aNBAq52zs7PW6SF120aNGhV4jSZNmmhtq6jXdnBwAAB4enoWWK5UKgutvyhyuRwLFizAuXPnsG/fvlKvVxwPD48CY38cHBwKrRd4+h4+6/n3sV69ejAxMdGccrtx4waEEGjQoEGB0HrlyhXcv39fa313d3eYm5trLevatSsGDx6MDz74AE5OThg4cCC2bNlS6nE3RFWFV9MQFaJ9+/aaq2kK07hxY5w7dw55eXkFvgAKawsAFy9exMCBAzXLbW1tERAQAEA1rqS05HK5Zj0A6NWrFxo3bow333wTP//8s2b59OnTsWXLFsycORMdO3aEg4MDZDIZhg8fDqVSWeh2C1NRvQnFKeq1K6qmUaNG4cMPP8SSJUswaNCgAs8XdaWNQqEoU10vUu/zNSiVSshkMvz222+Fbvf5nrbnw6h6m3v27MGJEyfwyy+/4PDhw3j99dfx+eef48SJEwW2QSQV9owQlUP//v3x+PFj/PTTTyW29ff3h4ODA3bt2lVoCHhRrq6uePfdd/HLL79oDUzcs2cPxo0bh88//xxDhgxBjx490KVLl0InYysNLy8vAKq/2J+VnJxc4C9/Ly8vXLt2rcA2rl69qrWtqvJs78j+/fsLPK/u2Xn+vXm+B6ciPf8+3rx5E0qlEt7e3gBUPSVCCNSpUwcBAQEFHh06dCj1a3Xo0AEfffQRTp8+je3bt+PSpUvYtWtXRe4O0QthGCEqh7feeguurq547733cP369QLP379/H0uXLgUAWFtb4//9v/+HixcvYu7cuYX+lfyivQ/Tp0+HtbU1PvnkE80yuVxeYLtr1qwp8q/9kgQEBMDMzAxr1qzR2u7KlSsLtO3bty8iIyMRERGhWZaVlYWNGzfC29sbTZs2LVcNL2L06NGoX78+PvjggwLP1atXDwDw119/aZYpFAps3Lix0upZt26d1s9r1qwBoJrjBgACAwMhl8vxwQcfFDiOQohSjS96+PBhgXVbtWoFADxVQzqFp2mIyqFatWrYu3cv+vbti1atWmnNwBoVFYWdO3eiY8eOmvZz587FlStXsHz5cvz+++8YPHgwPDw88PDhQ0RFReHHH39EzZo1YWlpWa56atSogQkTJuDLL7/ElStX0KRJE/Tr1w/ff/89HBwc0LRpU0RERODo0aOay5PLytnZGbNnz0ZwcDD69euHvn374uzZs/jtt9/g5OSk1Xbu3LnYuXMn+vTpg3feeQfVq1fHt99+i+joaPz0008wMan6v4Pkcjn+97//FRjkCQDNmjVDhw4dMG/ePDx48ADVq1fHrl27yjRQtqyio6MxYMAA9O7dGxEREdi2bRtGjhwJHx8fAKqAtHTpUsybNw8xMTEYNGgQ7OzsEB0djb1792Ly5MmYPXt2sa/x7bff4ssvv8Rrr72GevXqITMzE5s2bYK9vT369u1baftGVFYMI0Tl5Ofnh4sXL2L58uX49ddf8f3338PExARNmjTB3LlzteboMDExwffff4/Bgwdj06ZNWLNmDR4+fAhbW1s0b94cH330ESZNmvRC5/BnzZqFDRs24NNPP8XWrVuxatUqyOVybN++HTk5OejcuTOOHj2qNRC3rJYuXQpLS0ts2LABYWFh8PPzw++//45XX31Vq52LiwuOHz+OOXPmYM2aNcjJyUHLli3xyy+/FGhblUaPHo2lS5dq5o151vbt2/Hmm2/ik08+gaOjIyZOnIju3bujR48elVLL7t27sWjRIsydOxempqaYNm0ali9frtVm7ty5aNiwIb744gtNj46npyd69uyJAQMGlPgaXbt2RWRkJHbt2oWkpCQ4ODigffv22L59O+rUqVMp+0VUHjJRFaPTiIiIiIrAMSNEREQkKYYRIiIikhTDCBEREUmKYYSIiIgkxTBCREREkmIYISIiIknpxTwjSqUS9+7dg52dXZH3kCAiIiLdIoRAZmYm3Nzcip3sUC/CyL179wrcDZOIiIj0Q1xcHDw8PIp8Xi/CiPoW7HFxcbC3t5e4GiIiIiqNjIwMeHp6ar7Hi6IXYUR9asbe3p5hhIiISM+UNMSCA1iJiIhIUgwjREREJCmGESIiIpKUXowZIdJHQgjk5+dDoVBIXQoZALlcDlNTU05vQAaJYYSoEuTl5SEhIQHZ2dlSl0IGxNraGq6urjA3N5e6FKIKxTBCVMGUSiWio6Mhl8vh5uYGc3Nz/jVLL0QIgby8PCQnJyM6OhoNGjQodgIpIn3DMEJUwfLy8qBUKuHp6Qlra2upyyEDYWVlBTMzM8TGxiIvLw+WlpZSl0RUYRitiSoJ/3KlisbfKTJU7Bkhw6NQAMeOAQkJgKsr4O8PyOVSV0VEREVgGCHDEhICzJgB3L37dJmHB7BqFRAYKF1dRERUJPb5keEICQGGDNEOIgAQH69aHhIiTV1ERFQshhEyDAqFqkdEiILPqZfNnKlqR0UaP348ZDIZZDIZzM3NUb9+fSxZsgT5+fkAVFd1bNy4EX5+frC1tYWjoyPatm2LlStXal3GnJGRgYULF6JZs2awsrJCjRo10K5dOyxbtgwPHz6UaveISEfxNA0ZhmPHCvaIPEsIIC5O1a5btyor64VJMP6ld+/e2LJlC3Jzc3Hw4EFMnToVZmZmmDdvHsaMGYOQkBAsWLAAa9euhbOzM/7991+sXLkS3t7eGDRoEB48eIAuXbogIyMDH374IXx9feHg4IBr165hy5Yt2LFjB6ZOnVqp+0BEpbf0r6XIyc/BpDaT4OXoJUkNDCNkGBISKradLpBo/IuFhQVq1aoFAJgyZQr27t2Ln3/+GfXq1cP27duxb98+DBw4UNPe29sbAwYMQEZGBgBg/vz5uHPnDq5fvw43NzdNOy8vL/Ts2RPimd6rL7/8El988QXi4uLg4OAAf39/7Nmzp9L2jYi05SnysPLESqQ+ToV/bX+GEaIX4upase2kph7/8vxpJ/X4lz17qmxArpWVFVJTU7F9+3Y0atRIK4ioyWQyODg4QKlUYvfu3Rg9erRWEHm+LQCcPn0a77zzDr7//nt06tQJDx48wLFjxyp1X4hI2+Gbh5H6OBW1bGvhlbqvSFYHx4yQYfD3V/UaFDXTqUwGeHqq2uk6HRn/IoTA0aNHcfjwYbz88su4ceMGGjVqVOw6ycnJSEtLK9DO19cXtra2sLW1xYgRIwAAd+7cgY2NDfr16wcvLy+0bt0a77zzTqXtDxEV9P357wEAI5qPgKmJdP0TDCNkGORy1ekLoGAgUf+8cqV+zDdSlvEvleDAgQOwtbWFpaUl+vTpg6CgILz//vtap1fKau/evTh37hx69eqFx48fAwB69OgBLy8v1K1bF2PGjMH27dt5Lx+iKpSek46fr/0MABjdcrSktTCMkOEIDFSdvnB3117u4VGlpzVemMTjX7p3745z587hxo0bePz4Mb799lvY2NigYcOGuHr1arHrOjs7w9HREdeuXdNaXrt2bdSvXx92dnaaZXZ2doiKisLOnTvh6uqKRYsWwcfHB2lpaZWxW0T0nJ+u/IRcRS6aOjdF61qtJa2FYYQMS2AgEBMDhIUBO3ao/o2O1p8gAkg+/sXGxgb169dH7dq1YWr6tNt25MiRuH79Ovbv319gHSEE0tPTYWJigmHDhmHbtm24d+9eia9lamqKgIAALFu2DOfPn0dMTAz++OOPCt0fIiqc+hTN6BajJb+ZJ8MIGR65XHX57ogRqn/14dTMs3R0/MuwYcMQFBSEESNG4OOPP8bp06cRGxuLAwcOICAgAGFhYQCAjz/+GO7u7mjfvj02b96M8+fP49atW9i7dy8iIiIg/+94HDhwAKtXr8a5c+cQGxuL7777DkqlssRxKUT04u6k30F4TDgAYGSLkdIWA15NQ6R71ONfhgxRBY9nx2pIOP5FJpNhx44d2LhxIzZv3oyPPvoIpqamaNCgAcaOHYtevXoBAGrUqIHIyEh8+umnWL58OaKjo2FiYoIGDRogKCgIM2fOBAA4OjoiJCQE77//PnJyctCgQQPs3LkTzZo1q9L9IjJGOy7sAAB09eoq2eW8z5KJFxmVVkUyMjLg4OCA9PR02NvbS10OUbFycnIQHR2NOnXqvNht3gubZ8TTUxVE9Om0E1WYCvvdIqMmhEDz9c1xOfkyNvXfhDfavFFpr1Xa72/2jBDpqsBAYOBA3oGYiCrUv0n/4nLyZVjILTCk6RCpywHAMEKk29TjX4iIKsj3/6oGrvZv1B+Olo7SFvMfDmAlIiIyEgqlAjsuqsaLjG4h7dwiz2IYISIiMhKh0aFIfJSI6lbV0adBH6nL0WAYISIiMhLbzm8DAAQ1C4K53Fziap5iGCEiIjICWXlZCLkSAgAY03KMxNVoYxghIiIyAvuu7kPWkyzUrVYXHTw6SF2OFoYRIiIiI7DtguoUjS5M//48hhEiIiIDl/goEb/f+h2A9HfoLQzDCBFJJjw8HDKZjHfqJapkuy7uglIo4efuhwY1GkhdTgEMI0SkkZycjClTpqB27dqwsLBArVq10KtXL/zzzz8vvO1u3bpp7kuj1qlTJyQkJMDBweGFth0TEwOZTIZz58690HYAYPz48ZDJZJDJZDA3N0f9+vWxZMkS5Ofna9oIIbBx40b4+fnB1tYWjo6OaNu2LVauXIns7GxNu4yMDCxcuBDNmjWDlZUVatSogXbt2mHZsmV4+PDhC9dKVFrqq2h0sVcE4AysRPSMwYMHIy8vD99++y3q1q2LpKQkhIaGIjU1tdzbzMvLg7l54ZcQmpubo1atWuXetnr7Fa13797YsmULcnNzcfDgQUydOhVmZmaYN28eAGDMmDEICQnBggULsHbtWjg7O+Pff//FypUr4e3tjUGDBuHBgwfo0qULMjIy8OGHH8LX1xcODg64du0atmzZgh07dmDq1KkVXjvR864kX8GZhDMwNTFFULMgqcspnNAD6enpAoBIT0+XuhSiEj1+/FhcvnxZPH78WLNMqVSKR7mPJHkolcpS1f3w4UMBQISHhxfbLjY2VgwYMEDY2NgIOzs7MXToUJGYmKh5fvHixcLHx0ds2rRJeHt7C5lMJsaNGycAaD2io6NFWFiYACAePnyoWf/YsWOiS5cuwtLSUnh4eIjp06eLR48eaZ738vISS5YsEWPGjBF2dnaFbrtr166a9ps2bRKNGzcWFhYWolGjRmLdunXF7t+4cePEwIEDtZb16NFDdOjQQQghxO7duwUAsW/fvgLrKpVKkZaWJoQQ4s033xQ2NjYiPj6+0Nd59risW7dO1K9fX1hYWIiaNWuKwYMHF7pOYb9bRCWZf3S+wPsQ/Xb0q/LXLu33N3tGiKpA9pNs2AbbSvLaj+Y9go25TYntbG1tYWtri3379qFDhw6wsLAo0EapVGLgwIGwtbXFn3/+ifz8fEydOhVBQUEIDw/XtLt58yZ++uknhISEQC6Xw8vLC9evX0fz5s2xZMkSAICzszNiYmK0tn/r1i307t0bS5cuxebNm5GcnIxp06Zh2rRp2LJli6bdZ599hkWLFmHx4sUAgKlTp6J9+/Y4evQomjVrpumJ2b59OxYtWoS1a9eidevWOHv2LCZNmgQbGxuMGzeu1O+hlZWVpndo+/btaNSoEQYOHFignUwmg4ODA5RKJXbv3o3Ro0fDzc2t0G2qr2Y4ffo03nnnHXz//ffo1KkTHjx4gGPHjpW6NqLiKIUS2y9sB6B7c4s8i2GEiAAApqam2Lp1KyZNmoQNGzagTZs26Nq1K4YPH46WLVsCAEJDQ3HhwgVER0fD09MTAPDdd9+hWbNmOHXqFNq1awdAderku+++g7Ozs2b75ubmsLa2Lva0THBwMEaNGqUZW9KgQQOsXr0aXbt2xfr162FpaQkAePnll/Hee+9p1pP/dyfjGjVqaG1/8eLF+PzzzxEYGAgAqFOnDi5fvoyvvvqqVGFECIHQ0FAcPnwY06dPBwDcuHEDjRo1Kna95ORkpKWlFWjn6+uLa9euAQD69++PnTt34s6dO7CxsUG/fv1gZ2cHLy8vtG7dusTaiErj7zt/IzY9FnbmdujfsL/U5RSJYYSoClibWePRvEeSvXZpDR48GK+++iqOHTuGEydO4LfffsOyZcvw9ddfY/z48bhy5Qo8PT01QQQAmjZtCkdHR1y5ckUTRry8vLSCSGn9+++/OH/+PLZv365ZJoSAUqlEdHQ0mjRpAgBo27ZtidvKysrCrVu3MHHiREyaNEmzPD8/v8QBswcOHICtrS2ePHkCpVKJkSNH4v3339fUU1579+5FXl4e5syZg8ePHwMAevToAS8vL9StWxe9e/dG79698dprr8HauvTHjago6oGrQ5oOgZWZlcTVFI1hhKgKyGSyUp0q0QWWlpbo0aMHevTogYULF+KNN97A4sWLMX78+FJvw8amfPv66NEjvPnmm3jnnXcKPFe7du0ybf/RI1X427RpE/z8/LSeU/ekFKV79+5Yv349zM3N4ebmBlPTp/+rbNiwIa5evVrs+s7OznB0dNT0gjy/D3Z2dprLme3s7BAVFYXw8HD8/vvvWLRoEd5//32cOnUKjo6OJe4nUVFy8nPww6UfAOj2KRqAl/YSUQmaNm2KrKwsAECTJk0QFxeHuLg4zfOXL19GWloamjZtWux2zM3NoVAoim3Tpk0bXL58GfXr1y/wKOqKHPW2AWht38XFBW5ubrh9+3aBbdWpU6fYOmxsbFC/fn3Url1bK4gAwMiRI3H9+nXs37+/wHpCCKSnp8PExATDhg3Dtm3bcO/evWJfC1CdIgsICMCyZctw/vx5xMTE4I8//ihxPaLi/Hr9V6TnpsPD3gNdvbtKXU6xGEaICACQmpqKl19+Gdu2bcP58+cRHR2NH3/8EcuWLdMM1gwICECLFi0watQoREVFITIyEmPHjkXXrl1LPHXi7e2NkydPIiYmBikpKVAqlQXazJkzB8ePH8e0adNw7tw53LhxA/v378e0adOK3XbNmjVhZWWFQ4cOISkpCenp6QCADz74AMHBwVi9ejWuX7+OCxcuYMuWLVixYkU53yVg2LBhCAoKwogRI/Dxxx/j9OnTiI2NxYEDBxAQEICwsDAAwMcffwx3d3e0b98emzdvxvnz53Hr1i3s3bsXERERmt6ZAwcOYPXq1Th37hxiY2Px3XffQalUljguhagk6unfRzYfCROZjn/dV8GVPS+Ml/aSPtHXyy9zcnLE3LlzRZs2bYSDg4OwtrYWjRo1EgsWLBDZ2dmadqW9tPd5165dEx06dBBWVlbFXtobGRkpevToIWxtbYWNjY1o2bKl+OijjzTPe3l5iS+++KLA9jdt2iQ8PT2FiYmJ1qW927dvF61atRLm5uaiWrVq4qWXXhIhISFFvg+FXdr7PIVCIdavXy/atWsnrK2thb29vfD19RWrVq3Seq/S0tLEvHnzNJcWW1lZiZYtW4qFCxeK1NRUIYTqUuauXbuKatWqaZ7fvXt3oa+rr79bVPVSslKE2RIzgfchLiRdkKyO0n5/y4R4gdFYVSQjIwMODg5IT0+Hvb291OUQFSsnJwfR0dGoU6eO5uoPoorA3y0qrQ2nN2DKr1Pg4+KDc2+dk6yO0n5/63i/DREREZXV9+e/B6D7A1fVGEaIiIgMyO2Ht3E87jhkkGFEixFSl1MqDCNEREQGZPt51Tw9r9R9BW52hc8ArGsYRoiIiAyEEELvTtEADCNElUYPxoaTnuHvFJXk1L1TuPHgBqxMrfBa49ekLqfUGEaIKpiZmRkAIDs7W+JKyNCof6fUv2NEz1NP//5ak9dgZ2EncTWlx+ngiSqYXC6Ho6Mj7t+/DwCwtrbW3KGVqDyEEMjOzsb9+/fh6OhY4nT2ZJyeKJ5g18VdAIDRLUZLXE3ZMIwQVQL1nWPVgYSoIjg6OhZ712Mybr/f+h3J2cmoaVMTPer1kLqcMmEYIaoEMpkMrq6uqFmzJp48eSJ1OWQAzMzM2CNCxVIPXB3RfARMTfTr612/qiXSM3K5nF8gRFTpMnIzsP+a6uaNo1vq1ykagANYiYiI9F7IlRDk5OegUY1G8HX1lbqcMmMYISIi0nPPzi2ijwPmGUaIiIj02N2MuwiLDgMAjGo5SuJqyodhhIiISI/tuLADAgL+tf3h7egtdTnlUq4wsm7dOnh7e8PS0hJ+fn6IjIwstv3KlSvRqFEjWFlZwdPTE++++y5ycnLKVTARERE9pZ7oTB8HrqqVOYzs3r0bs2bNwuLFixEVFQUfHx/06tWryPkUduzYgblz52Lx4sW4cuUKvvnmG+zevRvz589/4eKJiIiM2fmk87hw/wLM5eYY2nSo1OWUW5nDyIoVKzBp0iRMmDABTZs2xYYNG2BtbY3NmzcX2v748ePo3LkzRo4cCW9vb/Ts2RMjRowotjclNzcXGRkZWg8iIiLS9v2/qoGr/Rr2QzWrahJXU35lCiN5eXk4c+YMAgICnm7AxAQBAQGIiIgodJ1OnTrhzJkzmvBx+/ZtHDx4EH379i3ydYKDg+Hg4KB5eHp6lqVMIiIig6dQKrDj4g4A+jf9+/PKNOlZSkoKFAoFXFxctJa7uLjg6tWrha4zcuRIpKSkoEuXLhBCID8/H2+99Vaxp2nmzZuHWbNmaX7OyMhgICEiInpGWEwY7mXeQzXLaujboOg/8PVBpV9NEx4ejo8//hhffvkloqKiEBISgl9//RUffvhhketYWFjA3t5e60FERERPqQeuDms2DBamFhJX82LK1DPi5OQEuVyOpKQkreVJSUlF3rxp4cKFGDNmDN544w0AQIsWLZCVlYXJkyfjf//7H0xMeHUxERFRWWQ/ycZPV34CoN9X0aiVKQmYm5vD19cXoaGhmmVKpRKhoaHo2LFjoetkZ2cXCBzqe3UIIcpaLxERkdHbf3U/HuU9grejNzp7dpa6nBdW5hvlzZo1C+PGjUPbtm3Rvn17rFy5EllZWZgwYQIAYOzYsXB3d0dwcDAAoH///lixYgVat24NPz8/3Lx5EwsXLkT//v15AzEiIqJy2Hbhv7lFWozWy+nfn1fmMBIUFITk5GQsWrQIiYmJaNWqFQ4dOqQZ1Hrnzh2tnpAFCxZAJpNhwYIFiI+Ph7OzM/r374+PPvqo4vaCiIjISNzPuo/DNw8DMIxTNAAgE3pwriQjIwMODg5IT0/nYFYiIjJqq0+uxoxDM9DOrR0iJxU/A7rUSvv9zdGjREREesQQpn9/HsMIERGRnriWcg2n7p2CXCbH8ObDpS6nwjCMEBER6Ql1r0iv+r1Q06amxNVUHIYRIiIiPSCE0LqKxpAwjBAREemBf+L+QUxaDGzNbTGw8UCpy6lQDCNERER6QH2KZnCTwbA2s5a4mopV5nlGiIiIKpRCARw7BiQkAK6ugL8/wEkxteTm5+KHSz8AMKyraNQYRoiISDohIcCMGcDdu0+XeXgAq1YBgYHS1aVjDt44iIc5D+Fm54bu3t2lLqfC8TQNERFJIyQEGDJEO4gAQHy8anlIiDR16SD1wNWRzUdCbmJ4vUYMI0REVPUUClWPSGGTgKuXzZypamfkHj5+iAPXDwAAxviMkbiaysHTNEREVPWOHSvYI/IsIYC4OFW7bt2qrCxdkafIw/mk84iMj8SB6weQp8hDi5ot0NKlpdSlVQqGESIigIMoq1pCQsW202NKocSN1BuIjI9UPe5F4lziOeQp8rTavd76dYkqrHwMI0REHERZ9VxdK7adHknITNAKHqfiTyE9N71Au+pW1dHevT3au7VHR8+O6FG3hwTVVg3etZeIjJt6EOXz/yuUyVT/7tnDQFIZFArA21s1WLWwryGZTBUIo6P1uocqIzcDp++d1oSPU/dO4W5GwdNTlqaW8HX1VYUP9/Zo59YOdavVhUz9e6inSvv9zZ4RIjJeJQ2ilMlUgygHDtTrL0SdJJerep6GDFG9z88eA/UX8MqVevW+PzvOQ/24mnIVAtq/XyYyEzRzbqYJHu3d26OZczOYyc0kqlx6DCNEZLw4iFJagYGqnqfCTpGtXKkXPVI5+TnYdXEXvo76GqfunSowzgMAvB29Nadb2ru3R2vX1rA1t5WgWt3FMEJExouDKKUXGKjqedKzwcP3Mu/hy1Nf4qszXyElO0WzvIZVDbRzb6cJHu3c2xnU3XUrC8MIERkvIx5EqVPkcr3peTpx9wRWnVyFPZf3IF+ZDwDwtPfEtPbTMLjJYIMY5yEFhhEiMl7+/qpTAiUNovT3r/raSGfkKfLw46UfsTpyNSLjIzXL/Wv7Y4bfDAxsPBCmJvw6fRF894jIeBngIEqqOEmPkvDVma+w/vR6JD5KBACYy80xssVIvNP+HbR2bS1xhYaDYYSIjJsBDKKkinXm3hmsjlyNXRd3aQakutq64u12b2Oy72SOAakEDCNExoSzjBZOTwdRUsV5oniCvVf3YvXJ1fgn7h/N8g4eHfBO+3cwuOlgmMvNJazQsDGMEBkLzjJaPD0aREkVJyU7BZvObMKXp7/UTEZmZmKGYc2G4R2/d9Devb3EFRoHhhEiY1DULKPqW7VzllEyMueTzmP1ydXYfmE7cvJzAAA1bWriLd+38Fbbt+BqxyuoqhKngycydOppt4ua3MtApt0mKolCqcAv13/BqpOrEB4TrlnexrUNZvjNQFCzIFiYWkhXoAHidPBEpMJZRslIPX7yGNdTr+PK/Uu4eOY3bL93GDH5yQAAuUyOwCaBmOE3A508O3FuEIkxjBAZOs4ySgYuJTsFV5Kv4GrKVVxJefpvbFpsgfvCVM8GJl+3w9tBn8Fz6GSJKqbnMYwQGTrOMkoGQKFUIDY9VhU0ngseqY9Ti1yv2mOgSTLQOAXocgcYfhGwUjwC9r8FmDtxrJSO4JgRIkNnSLdq56XJBk9zaiVFO3BcT72uGWhaGC8HLzRxboLGNRqr/q3WAI17jYLzzQQUegJGn37v9RjHjBCRiqHMMspLk/WeEAKpj1NxN+Mu7mbcRVx6nOq/M1U/3354u9BTK2oWcgs0rNFQEzoaO6mCR8MaDWFtZq3dODwcuFnMqUeOldIpDCNExkDfZxnlpck6TwiBlOwUxGXEacLG3Yy7BX4urndDrbpVdTRxaqIKG//929ipMbwdvSE3KWVo5lgpvcIwQmQs9HWWUYVCFaIKO8UkhKp3Z+ZM1b7p+r7osczcTNx4cANx6XGFBo74jHjkKnJLtS0XGxd42HvAw94Dnvaemv+u7VAbjZ0aw9nG+cUL5lgpvcIwQmRM9HGWUV6aXGWEELiXeU9rrIb6EZ8ZX6pt1LKtVWjQUP+3m51b1czlwTsy6xWGESLSbexur3B5ijzcfHBTEzSeDR6P8h4VuV7NR4BXOuCZDngobeER8Bo8O/fVBA43OzfduX+LoYyVMhIMI0Sk29jdXm4PHz/U6t24mqq6LPb2w9tQCEWh68hlctSrXu/peI3YR2j8/jo0SgGqPTvcQ5YF/LQN2DMICOxSJftTZvo+VsqI8NJeItJthnRpciUSQuDbf7/FibsnNOEjKSupyPZ25naagaHPDhStV73e094NQ7mVAC8Jlwwv7SUiw8Du9lL55fovmLB/QoHlHvYeqsDxzKWwjZ0aw9XWteQp0A1lvI4+jpUyMgwjRKT72N1eog2nNwAA+jboixHNR6CJk2r+DTsLu/JvlON1qIowjBCRftDXS5OrQGxaLA7dPAQAWNV7FepXr18xG+Z4HaoiDCNEpD/Y3V6ob85+AwGBV+q8UnFBBODlsVRlTKQugIiIyi9fmY9vzn4DAJjsW8F3oVWP1wGejs9R43gdqkAMI0REeuzgjYO4l3kPztbOGNR4UMW/gHq8jru79nIPD07DTxWGp2mIiPTYxjMbAQDjW42vvAnHOF6HKhnDCBGRnrqTfge/3fwNAPBGmzcq98U4XocqEU/TEBHpqW+ivoFSKNHduzsa1mgodTlE5cYwQkSkhyp14CpRFWMYISLSQ7/d+A3xmfFwsnbCa41fk7ocohfCMEJEpIc2Rv03cNVnPCxMLSSuhujFMIwQEemZuPQ4HLxxEAAwyXeSxNUQvTiGESIiPbP57GYohRLdvLtx4CoZBIYRIiI9kq/Mx9dnvwYATG7DgatkGBhGiIj0yKGbh3A34y5qWNXAa004cJUMA8MIEZEeUc+4Os5nHCxNLSWuhqhiMIwQEemJuxl38euNXwFwbhEyLAwjRER6Qj1wtatXVzRyaiR1OUQVhmGEiEgPKJQKfB3138BV9oqQgWEYISLSA4dvHUZcRhyqW1VHYJNAqcshqlAMI0REeuCrM18B4MBVMkwMI0REOi4+Ix4Hrh8AAExqwxlXyfAwjBAR6Tj1wFX/2v5o4txE6nKIKhzDCBGRDlMoFZoZV9/0fVPiaogqB8MIEZEO+/3W77iTfgfVLKthcNPBUpdDVCkYRoiIdNjGKM64SoaPYYSISEfdy7yHX679AgCY5MuBq2S4yhVG1q1bB29vb1haWsLPzw+RkZHFtk9LS8PUqVPh6uoKCwsLNGzYEAcPHixXwURExmLz2c1QCAW61O6Cps5NpS6HqNKYlnWF3bt3Y9asWdiwYQP8/PywcuVK9OrVC9euXUPNmjULtM/Ly0OPHj1Qs2ZN7NmzB+7u7oiNjYWjo2NF1E9EZJC0ZlxtwxlXybDJhBCiLCv4+fmhXbt2WLt2LQBAqVTC09MT06dPx9y5cwu037BhA5YvX46rV6/CzMysXEVmZGTAwcEB6enpsLe3L9c2iIj0yaGbh9Bnex9Us6yG+FnxsDKzkrokojIr7fd3mU7T5OXl4cyZMwgICHi6ARMTBAQEICIiotB1fv75Z3Ts2BFTp06Fi4sLmjdvjo8//hgKhaLI18nNzUVGRobWg4jImGw8oxq4OtZnLIMIGbwyhZGUlBQoFAq4uLhoLXdxcUFiYmKh69y+fRt79uyBQqHAwYMHsXDhQnz++edYunRpka8THBwMBwcHzcPT07MsZRIR6bWEzAT8fO1nAJxxlYxDpV9No1QqUbNmTWzcuBG+vr4ICgrC//73P2zYsKHIdebNm4f09HTNIy4urrLLJCLSGVvObYFCKNDZszOa1WwmdTlEla5MA1idnJwgl8uRlJSktTwpKQm1atUqdB1XV1eYmZlBLpdrljVp0gSJiYnIy8uDubl5gXUsLCxgYWFRltKIiAyCUiixKWoTAGCyLweuknEoU8+Iubk5fH19ERoaqlmmVCoRGhqKjh07FrpO586dcfPmTSiVSs2y69evw9XVtdAgQkRkzI7cOoKYtBg4WjpiaNOhUpdDVCXKfJpm1qxZ2LRpE7799ltcuXIFU6ZMQVZWFiZMmAAAGDt2LObNm6dpP2XKFDx48AAzZszA9evX8euvv+Ljjz/G1KlTK24viIgMhHrG1TEtx3DgKhmNMs8zEhQUhOTkZCxatAiJiYlo1aoVDh06pBnUeufOHZiYPM04np6eOHz4MN599120bNkS7u7umDFjBubMmVNxe0FEZACeHbjKUzRkTMo8z4gUOM8IERmD4GPBmP/HfHTy7IR/Xv9H6nKIXlilzDNCRESVQ2vgKmdcJSPDMEJEpANCb4ciOi0aDhYOGNqMA1fJuDCMEBHpgGcHrlqbWUtcDVHVYhghIpJY4qNE7Lu6DwAHrpJxYhghIpLY1nNbka/MRwePDmjh0kLqcoiqHMMIEZGEOHCViGGEiEhSf0T/gdsPb8PBwgFBzYOkLodIEgwjREQS2nhGNXB1dMvRHLhKRothhIhIIkmPkrD36l4AwKQ2kySuhkg6DCNERBJRD1z1c/eDTy0fqcshkgzDCBGRBLQGrvJyXjJyDCNERBIIiw7DrYe3YG9hj6BmHLhKxo1hhIhIAuoZV0e3GA0bcxuJqyGSFsMIEVEVu591H3uvqAau8hQNEcMIEVGV+/bct3iifIL27u05cJUIDCNERFVKCKE5RcMZV4lUTKUugIyQQgEcOwYkJACuroC/PyCXS10VUZUIiwnDzQc3YWduxxlXif7DMEJVKyQEmDEDuHv36TIPD2DVKiAwULq6iKqIesbVUS1GwdbcVuJqiHQDT9NQ1QkJAYYM0Q4iABAfr1oeEiJNXURVJDkrGSFXVL/nHLhK9BTDCFUNhULVIyJEwefUy2bOVLUjMlDf/qsauNrOrR1au7aWuhwincEwQlXj2LGCPSLPEgKIi1O1IzIwQgjsu7oPKyJWAGCvCNHzOGaEqkZCQsW2I9IT4THhmHt0Lk7GnwQAeDt6Y3jz4RJXRaRbGEaoari6Vmw7Ih135t4ZzP9jPn6/9TsAwNrMGjP9ZuL/Ov8fB64SPYdhhKqGv7/qqpn4+MLHjchkquf9/au+NqIKdC3lGhaGLcSPl38EAJiamGJym8lY8NICuNoxbBMVhmGEqoZcrrp8d8gQVfB4NpDIZKp/V67kfCOkt+5m3MWSP5dg89nNUAgFZJBhZIuR+KDbB6hXvZ7U5RHpNIYRqjqBgcCePYXPM7JyJecZIb2Ump2KT/7+BGsi1yBXkQsA6NewHz56+SO0dGkpcXVE+oFhhKpWYCAwcCBnYCW99yjvEVaeWInlx5cjIzcDAOBf2x/BrwSjc+3OEldHpF8YRqjqyeVAt25SV0FULrn5udh4ZiOWHluK+1n3AQA+Lj4IfiUYvev3hkx92pGISo1hhIioFBRKBbZf2I5FYYsQmx4LAKhXrR4+7P4hgpoHwUTGaZuIyothhKiseKM/oyKEwM/Xfsb//vgfLiVfAgC42rpiUddFmNh6IszkZhJXSKT/GEaIyoI3+jMq4THhmBc6DyfungAAOFo6Ym7nuZjuNx3WZtYSV0dkOBhGiEpLfaO/5+dJUd/ob88eBhIDEZUQhfmh83H41mEAgJWpFWZ2mIn/6/R/qGZVTeLqiAyPTIjCZqDSLRkZGXBwcEB6ejrs7e2lLoeMkUIBeHsXfX8d9aRt0dE8ZaPHrqZcxeLwxfjh0g8AOGEZ0Ysq7fc3e0aISqMsN/rjlUJ658y9Mwj+OxghV0IgIDhhGVEVYxghKg3e6M/gCCHwV+xf+PjvjzX3jwGAgY0G4oNuH8Cnlo+E1REZF4YRotLgjf4MhhACB28cxMd/f4zjcccBAHKZHCNajMCcznPQvGZziSskMj4MI0SlwRv96T2FUoEfL/+I4L+DcT7pPADAQm6B11u/jv/r9H+oU62OxBUSGS+GEaLS4I3+9FZufi6++/c7LDu+DDcf3AQA2JrbYkrbKXi3w7scmEqkAxhGiEqLN/rTK1l5Wdh4ZiM+i/gM9zLvAQCqW1XHDL8ZmNZ+GqpbVZe4QiJSYxghKgve6E/nPXz8EGsj12LVyVVIfZwKAHCzc8PsjrMxyXcSbM1tJa6QiJ7HMEJUVrzRn05KyEzAFye+wPrT6/Eo7xEA1b1j5naZizEtx8DC1ELiCslg8RYRL4xhhIj0WvTDaCw/vhybz25GriIXANCiZgvM95+PIU2HwNSE/5ujSsRbRFQIfkqJSC9dun8Jn/zzCXZe2AmFUAAAOnp0xHz/+Xi1wauQqQcWE1UW3iKiwnA6eCKqOJXcXZ2vzMep+FNYdnwZ9l3dp1nes15PzO8yHy95vcQQQlWDt4goFU4HT0RVq4K6q4UQuJd5D9dTr+N66nXceHBD89+3H97GE+UTAIAMMgQ2CcS8LvPg6+Zb0XtDVDzeIqJCMYwQ0YsrR3d1anZqoYHjxoMbyH6SXeRLWZlaYWizoZjbeS6aODepjL0hKhlvEVGhGEaI6MUoFKoekULO+D4yE7hRA7i+ajJuVL+I6w9vakLHw5yHRW5SLpOjTrU6aFijIRpWb4gGNRqo/rtGQ3jYe8BEZlKZe0RUMt4iokIxjBDRizl2DMr4u7jqDJx0ByLdgSvOwPUaQIKdulEq8OfiAqt62HtoAkfDGk9DRx3HOjCTm1XpbhCVCW8RUaEYRoh0iZ7MV5D0KAkn40/i5N2TOBm1H6fmABmWhbd1zgIapAINm7+Ehm17awJH/er1YW1mXbWFE1UU3iKiQjGMEOkKHZ2v4PGTx4hKiFKFj/8CSGx6rHYjS8A6D/BNAPzuAj5JQMNUVQiplvNfm7APAP9uVV0+UeXhLSIqDC/trSx68hcu6YiiBoCq/8KqovkKlEKJG6k3cDL+JE7cPYGT8SdxPuk88pX52mVBhibOTeDn7gc/13bwm/Q+ml+8D1NlIRvlJY5k6Pj/+yKV9vubYaQy6OhfuKSjJJyvIDkrGSfjTyIyPlLzb1pOWoF2LjYu8PPwU4UPdz+0c28He4tnPovqMAUU3l3NyZ+IjBLDiFR05C9c0iPh4UD37iW3Cwsrcb6CfGU+MnMzkZ6bjozcjAKP9BzV8lsPb+Fk/Encfni7wDYsTS3h6+qrCh7/BZDaDrVLnkyssBDu6cnuaiIjxjAiBc7IR+WxcycwcqTmxycmwGk34IEVkGGheqRbAhlBg5BR31M7XDwXOoqbn6MojZ0aa3o8/Dz80KJmi/JfycLuaiJ6BmdglQJn5KPyeG4eglm9gLV+hbR7sA+ILN0mrUytYG9hX+DhYOkAe3N71LKthfbu7dHOvR0cLR1fdA+e4h2NiagcGEYqEmfko/J4Zr6CB5YC37RRLW6dAFR7DNjnAg5ya9iPeh32lg7a4cLCoUDgsLOwg7ncXNp9IiIqA4aRisQZ+ag8npmvYEtr4LEZ0CoBOPMVno7T2PM90JfjLojIMHFO5Yqk/gu3qIF+MplqQB9n5KPnBQZC8eNufNlBNb5iWiQgA1S/Txz0TEQGjmGkIqn/wgUKBhLOyEclONTCGrftFahmaocR721RXT0THc0gQkQGj2Gkoqln5HN3117Ov3CpBGtPrQUATGz3JqxHjVcNBGVwJSIjwDEjlSEwEBg4kJc4UqndSL2BQzcPQQYZprSbInU5RERVimGksvASRyqD9afXAwD6NuiLutXqSlwNEVHV4mkaIoll5WVh89nNAIBp7adJXA0RUdVjGCGS2PYL25Gem4761eujZ72eUpdDRFTlyhVG1q1bB29vb1haWsLPzw+RkaWbFnLXrl2QyWQYNGhQeV6WyOAIIbA2UjVwdWq7qTCR8e8DIjI+Zf4/3+7duzFr1iwsXrwYUVFR8PHxQa9evXD//v1i14uJicHs2bPhzzk2iDSO3TmGC/cvwNrMGuNbjZe6HCIiSZQ5jKxYsQKTJk3ChAkT0LRpU2zYsAHW1tbYvHlzkesoFAqMGjUKH3zwAerW5eA8IjV1r8iYlmMq9h4xRER6pExhJC8vD2fOnEFAQMDTDZiYICAgABEREUWut2TJEtSsWRMTJ04s1evk5uYiIyND60FkaOIz4hFyJQSA6hQNEZGxKlMYSUlJgUKhgIuLi9ZyFxcXJCYmFrrO33//jW+++QabNm0q9esEBwfDwcFB8/D09CxLmUR64aszX0EhFHjJ6yW0cGkhdTlERJKp1NFymZmZGDNmDDZt2gQnJ6dSrzdv3jykp6drHnFxcZVYJVHVy1PkYeOZjQCAae14OS8RGbcyTXrm5OQEuVyOpKQkreVJSUmoVatWgfa3bt1CTEwM+vfvr1mmVCpVL2xqimvXrqFevXoF1rOwsICFhUVZSiPSKz9d/glJWUlws3PDoMaDpC6HiEhSZeoZMTc3h6+vL0JDQzXLlEolQkND0bFjxwLtGzdujAsXLuDcuXOax4ABA9C9e3ecO3eOp1/IaKnvQ/OW71swk5tJXA0RkbTKPB38rFmzMG7cOLRt2xbt27fHypUrkZWVhQkTJgAAxo4dC3d3dwQHB8PS0hLNmzfXWt/R0REACiwnMhZRCVE4HnccZiZmmOQ7SepyiIgkV+YwEhQUhOTkZCxatAiJiYlo1aoVDh06pBnUeufOHZiYcOImoqKsi1wHABjabChq2RY8vUlEZGxkQgghdRElycjIgIODA9LT02Fvby91OUTllpqdCo8vPJCTn4Pjrx9HR8+CpzeJiAxFab+/2YVBVIU2n92MnPwctHFtgw4eHaQuh4hIJzCMEFURhVKBL09/CUA1yZlMJpO4IiIi3cAwQlRFfrv5G2LSYlDdqjpGNB8hdTlERDqDYYSoiqjvQzOx9URYmVlJXA0Rke5gGCGqAtdTr+PwrcOQQYYpbadIXQ4RkU5hGCGqAl+eUo0V6dewH+pUqyNxNUREuoVhhKiSPcp7hC3ntgAAprXnfWiIiJ7HMEJUybad34aM3Aw0rNEQAXUDpC6HiEjnMIwQVSIhhGbg6ttt34aJjB85IqLn8f+MRJXoz9g/cSn5EmzMbDCu1TipyyEi0kkMI0SVaN0p1X1oxrQcA0dLR2mLISLSUQwjRJXkbsZd7L2yFwAwtf1UiashItJdDCNEleSr019BIRTo5t0NzWs2l7ocIiKdxTBCVAly83OxMWojAGBaO17OS0RUHIYRokqw5/Ie3M+6Dw97DwxsPFDqcoiIdBrDCFElWHtKdTnvm75vwtTEVOJqiIh0G8MIUQU7fe80Ttw9ATMTM0xqM0nqcoiIdB7DCFEFU1/OO6zZMLjYukhcDRGR7mMYIapAqdmp2HlhJwDeh4aIqLQYRogq0Ddnv0GuIhe+rr7wc/eTuhwiIr3AMEJUQRRKBb489SUAVa+ITCaTuCIiIv3AMEJUQX698Sti02NRw6oGgpoFSV0OEZHeYBghqiDqu/NObD0RVmZWEldDRKQ/GEaIKsDVlKs4cvsIZJBhSrspUpdDRKRXGEaIKoB6rEj/Rv3h7egtbTFERHqGYYToBWXmZmLrua0AeB8aIqLyYBghekHbzm9DZl4mGtVohFfqviJ1OUREeodhhOgFCCE096GZ2m4qTGT8SBERlRX/z0n0AsJjwnE5+TJszW0xrtU4qcshItJLDCNEL0DdKzK25VjYW9hLXA0RkX5iGCEqpzvpd7Dv6j4AwNvt3pa2GCIiPWYqdQFE+uqr019BKZTo7t0dzWo2k7ocMnYKBXDsGJCQALi6Av7+gFwudVVEpcIwQlQOOfk52Bi1EQDvzks6ICQEmDEDuHv36TIPD2DVKiAwULq6iEqJp2mIyuHHSz8iJTsFHvYeGNBogNTlkDELCQGGDNEOIgAQH69aHhIiTV1EZcAwQlQO6oGrU9pOgakJOxhJIgqFqkdEiILPqZfNnKlqR6TDGEaIyuhU/ClExkfCXG6ON9q8IXU5ZMyOHSvYI/IsIYC4OFU7Ih3GMEJURp9HfA4ACGoWhJo2NSWuhoxaQkLFtiOSCMMIURlEP4zGj5d/BAC81/E9iasho+fqWrHtiCTCMEJUBl+c+AJKoUSPuj3gU8tH6nLI2Pn7q66akckKf14mAzw9Ve2IdBjDCFEppWan4puz3wAA/q/T/0lcDRFU84isWqX67+cDifrnlSs53wjpPIYRolLacHoDsp9ko1WtVgioGyB1OUQqgYHAnj2Au7v2cg8P1XLOM0J6gNckEpVCTn4O1kSuAQDM7jgbsqK6xYmkEBgIDBzIGVhJbzGMEJXC9/9+j6SsJHjae2JYs2FSl0NUkFwOdOsmdRVE5cLTNEQlUAql5nLedzu8CzO5mcQVEREZFoYRohL8cu0XXEu9BgcLB05yRkRUCRhGiEqw/PhyAKqp3+0s7CSuhojI8DCMEBUjIi4C/8T9A3O5Od7xe0fqcoiIDBLDCFEx1L0io1uMhqsdZ7EkIqoMDCNERbieeh37ru4DAMzuNFvaYoiIDBjDCFERVkSsgIBAv4b90MS5idTlEBEZLIYRokLcz7qPree2AuDU70RElY1hhKgQayPXIleRi/bu7eFfmzcZIyKqTAwjRM/JysvCulPrAHDqdyKiqsAwQvScLee24MHjB6hbrS4Cm/AmY0RElY1hhOgZCqUCKyJWAABmdZgFuQlvNEZEVNkYRoieEXIlBNFp0ahhVQMTWk+QuhwiIqPAMEL0HyGEZpKzqe2mwtrMWuKKiIiMA8MI0X/+iv0Lp+6dgqWpJaa1nyZ1OURERoNhhOg/6l6R8T7j4WzjLHE1RETGg2GECMDl5Mv49cavkEGGWR1nSV0OEZFRYRghAvDZ8c8AAK81eQ0NajSQuBoiIuPCMEJG717mPWw7vw0Ap34nIpICwwgZvdUnV+OJ8gm61O6CDh4dpC6HiMjoMIyQUcvMzcSG0xsAsFeEiEgqDCNk1DZFbUJ6bjoaOzVGv4b9pC6HiMgolSuMrFu3Dt7e3rC0tISfnx8iIyOLbLtp0yb4+/ujWrVqqFatGgICAoptT1RVniieYOWJlQCA9zq+BxMZszkRkRTK/H/f3bt3Y9asWVi8eDGioqLg4+ODXr164f79+4W2Dw8Px4gRIxAWFoaIiAh4enqiZ8+eiI+Pf+HiiV7E7ku7EZcRBxcbF4xuOVrqcoiIjJZMCCHKsoKfnx/atWuHtWvXAgCUSiU8PT0xffp0zJ07t8T1FQoFqlWrhrVr12Ls2LGFtsnNzUVubq7m54yMDHh6eiI9PR329vZlKZeoUEIItPqqFc4nncfS7kvxv5f+J3VJREQGJyMjAw4ODiV+f5epZyQvLw9nzpxBQEDA0w2YmCAgIAARERGl2kZ2djaePHmC6tWrF9kmODgYDg4Omoenp2dZyiQq0ZHbR3A+6TxszGwwpd0UqcshIjJqZQojKSkpUCgUcHFx0Vru4uKCxMTEUm1jzpw5cHNz0wo0z5s3bx7S09M1j7i4uLKUSVQi9SRnE1tPRHWrooMxERFVPtOqfLFPPvkEu3btQnh4OCwtLYtsZ2FhAQsLiyqsjIzJucRzOHL7COQyOd7t+K7U5RARGb0yhREnJyfI5XIkJSVpLU9KSkKtWrWKXfezzz7DJ598gqNHj6Jly5Zlr5Sogqh7RYY2GwpvR29piyEiorKdpjE3N4evry9CQ0M1y5RKJUJDQ9GxY8ci11u2bBk+/PBDHDp0CG3bti1/tUQv6E76Hey6uAsAJzkjItIVZT5NM2vWLIwbNw5t27ZF+/btsXLlSmRlZWHChAkAgLFjx8Ld3R3BwcEAgE8//RSLFi3Cjh074O3trRlbYmtrC1tb2wrcFaKSrTyxEgqhwMt1XkYb1zZSl0NERChHGAkKCkJycjIWLVqExMREtGrVCocOHdIMar1z5w5MTJ52uKxfvx55eXkYMmSI1nYWL16M999//8WqJyqDtJw0bIraBIC9IkREuqTM84xIobTXKRMV55O/P8G80HloUbMF/n3rX8hkMqlLIiIyaJUyzwiRvsrNz8Wqk6sAALM7zWYQISLSIQwjZBS2X9iOxEeJcLdzx/Dmw6Uuh4iInsEwQgZPKZSay3lndpgJc7m5xBUREdGzGEbI4B28cRBXUq7AztwOk9pMkrocIiJ6DsMIGbzlx5cDAN70fRMOlg4SV0NERM9jGCGDFhkfib9i/4KpiSlmdJghdTlERFQIhhEyaOpekZEtRsLD3kPiaoiIqDBVeqM8oqp068EthFwJAQDM7jhb4mqIiMpBoQCOHQMSEgBXV8DfH5DLpa6qwjGMkMH64sQXUAoletfvjRYuLaQuh4iobEJCgBkzgLt3ny7z8ABWrQICA6WrqxLwNA0ZpJTsFGw+uxkAp34nIj0UEgIMGaIdRAAgPl61PCREmroqCcMIGaQvT32Jx/mP0ca1Dbp7d5e6HCKi0lMoVD0ihd2tRb1s5kxVOwPBMEIGJzYtFmsi1wBQ9Ypw6nci0ivHjhXsEXmWEEBcnKqdgWAYIYNyOfkyOm/ujJTsFDR2aowhTYeUvBIRkS5JSKjYdnqAA1jJYETGR6LP9j548PgBmjg1we9jfoepCX/FiUjPuLpWbDs9wJ4RMghHbx/Fy9++jAePH6CdWzv8NeEvzitCRPrJ31911UxRp5hlMsDTU9XOQDCMkN776fJPeHXHq8h6koWAugEIHRsKJ2snqcsiIiofuVx1+S5QMJCof1650qDmG2EYIb32ddTXGLZnGPIUeRjSdAgOjDgAOws7qcsiInoxgYHAnj2Au7v2cg8P1XIDm2eEJ9RJby37ZxnmHJ0DAJjUZhLWv7oechPD+UuBiIxcYCAwcCBnYCXSRUIIzDk6R3Pfmbmd5+LjVz7mJbxEZHjkcqBbN6mrqHQMI6RX8pX5eOvAW/jm7DcAgOU9lmN2J953hohInzGMkN7Iyc/BqJBRCLkSAhOZCb7u/zUmtJ4gdVlERPSCGEZIL2TmZmLQ7kH4I/oPmMvNsWvwLrzW5DWpyyIiogrAMEI6LyU7BX2298Hpe6dha26Ln4f/jO51eL8ZIiJDwTBCOi0uPQ49t/XE1ZSrcLJ2wm+jfkNbt7ZSl0VERBWIYYR01rWUa+jxfQ/EZcTB094Tv4/5HY2dGktdFhERVTCGEdJJZ+6dQe/tvZGSnYJGNRrh9zG/o7ZDbanLIiKiSsAwQjonPCYcA3YOQGZeJtq6tcXBkQfhbOMsdVlERFRJOB086ZR9V/eh97beyMzLRHfv7vhj7B8MIkREBo5hhHTG1nNbMfiHwchV5GJQ40E4OOog7zNDRGQEjPc0jUJhFPP964sVESvw3u/vAQBeb/U6vur/FUxNjPfXk4jImBhnz0hICODtDXTvDowcqfrX21u1nKqUEALzQ+drgsjsjrPx9YCvGUSIiIyI8YWRkBBgyBDg7l3t5fHxquUMJFVGoVTgrQNvIfjvYADAJ698guU9l/OGd0RERsa4wohCAcyYAQhR8Dn1spkzVe2oUuXm52LETyOwMWojTGQm2NhvI+Z0mSN1WUREJAHj6gs/dqxgj8izhADi4lTtjOCWzVVNCIHzSeex5/Ie7L60Gzce3IC53BzbA7djSNMhUpdHREQSMa4wkpBQse2oREIInE08iz2X92DP5T248eCG5jl7C3v8NOwnBNQNkLBCIiKSmnGFEVfXim1HhRJC4PS906oAcmUPbj+8rXnOQm6BPg36YEiTIejXsB8cLB0krJSIiHSBcYURf3/Aw0M1WLWwcSMymep5f/+qr03PCSEQGR+JHy//iD2X9yA2PVbznKWpJfo26IuhTYfi1Qavcu4QIiLSYlxhRC4HVq1SXTUjk2kHEvUVHCtXcr6RUs7BohRKnLh7Aj9e+hE/XfkJcRlxmueszazxaoNXMbTpUPRp0Ae25rZVuQdERKRHjCuMAEBgILBnj+qqmmcHs3p4qIJIYKBkpemEkJDC35tVq4DAQCiUChyPO449l/fgpys/IT4zXtPM1twW/Rr2w9CmQ9G7fm9Ym1lLsANERKRvZEIUdr5Ct2RkZMDBwQHp6emwt7evmI1yBtaC1HOwPPcroTABjtUG9szqjZ/yziHxUaLmOTtzOwxoNABDmg5Br3q9YGVmVdVVExGRjirt97fx9YyoyeW8fPdZz83Bkif/L4A0BUKaAPdtATw4BABwsHDAwMYDMaTJEPSo1wOWppYSFk5ERPrOeMMIaXnyZxhO4y7C/IEwb+Cf2sBjs6fPV3sMDLoKDBkTjFcGvgsLUwvJaiUiIsPCMGKk8pX5iEqIQlh0GMJiwvD37XBkvaHdxjkLGHANGHoJ6B4DmCsABHkBDCJERFSBGEb0VRnHvCiUCpxLPIewmDCEx4Tjr9i/kJmXqdWmejbQLUb16B4DNLsPFLhLDOdgISKiCsYwoo9KuOIFUF12ez7pPMKiwxAeqwofaTlpWptxtHREV6+u6ObdDd1rv4QWfgNgEn+Pc7AQEVGVYhjRN0Vc8aKMv4tLbw9GeMpEhDk8wJ+xf+LB4wdabewt7PGS10vo5tUN3et0h4+LD+Qmz/SmrFrNOViIiKjKGe+lvfpIoQC8vYG7d6GQAVedgD+9VQNOw72BFBvt5jZmNvD38kd37+7o7t0drV1bw9SkhPxZWK+LpyfnYCEiojLjpb0G5PGTx7hw/wLO/rkL53zu4mxv4LyL9tUuAGCdB3SOA7oHvIHuL0+Er6svzORmhW+0KIGBwMCBnIOFiMgY6MicWwwjOubB4wc4l3gOZxPO4mziWZxLPIerKVehEApVg3ZP29rkAX53VYNNu0cD7e79d8VLn5cBjw7lL4JzsBARGb5SjD+sKgwjEhFCIC4jTit4nE08izvpdwpt72ztjNYWXmj9y2m0SgRaJwD1HwDywk6y8YoXIiIqThHjDxEfr1q+Z0+VBhKOGakCCqUC11Kv4WyCqqdD3eOR+ji10PZ1HOugtWtrtK6lerSq1Qpudm6QKZWqMSMl3XU4OpqnVYh0jY50hxM9O/6wUBX4XcIxI1VMCIH7WfcRnRaN2w9vI/qh6t9LyZdwPuk8Huc/LrCOqYkpmjo3RatarTTBw6eWDxwtHQt/Ed51mEg/6VB3OBGOHSs6iACq75a4OFW7KjplzzBSBo/yHiH6YbR24Ei7rVmW/SS7yHVtzGzgU8tH09PRulZrNKvZrOz3deFdh4n0i451hxMhIaFi21UAhpFn5CvzEZcepwoa6sCRFq3p5UjOTi52fRlk8LD3QJ1qdVC3Wl3UcayDhjUaonWt1qhfvb72nB4vgle8EOmH525AqUUIVY/mzJmqzzM/v1RVSjuusArHHxp1GFlzcg3+TfpXEzjupN95etVKEapZVlMFjWp1UNdR9W8dR1X4qO1Qu+puIMcrXoh0nw52hxPB31/Vm17S+MMqnHHbqMPI9gvbcTL+pNYyC7kFvB29NT0bz/Zy1KlWp+jxHEREz9PB7nAiXRx/aNRhZHyr8ehTv49W4HC1c4WJzETq0ojIEOhgdzgRAJ0bf8hLe4mIKov6Ekpejk+6qpIvOeelvUREUtPB7nAiLToy/pDnI4iIKpO6O9zdXXu5hwcv6yX6D3tGiIgqGy/HJyoWwwgRUVXQke5wIl3E0zREREQkKYYRIiIiklS5wsi6devg7e0NS0tL+Pn5ITIystj2P/74Ixo3bgxLS0u0aNECBw8eLFexREREZHjKHEZ2796NWbNmYfHixYiKioKPjw969eqF+/fvF9r++PHjGDFiBCZOnIizZ89i0KBBGDRoEC5evPjCxRMREZH+K/OkZ35+fmjXrh3Wrl0LAFAqlfD09MT06dMxd+7cAu2DgoKQlZWFAwcOaJZ16NABrVq1woYNG0r1mpz0jIiISP+U9vu7TD0jeXl5OHPmDAICAp5uwMQEAQEBiIiIKHSdiIgIrfYA0KtXryLbA0Bubi4yMjK0HkRERGSYyhRGUlJSoFAo4OLiorXcxcUFiYmJha6TmJhYpvYAEBwcDAcHB83D09OzLGUSERGRHtHJq2nmzZuH9PR0zSMuLk7qkoiIiKiSlGnSMycnJ8jlciQlJWktT0pKQq1atQpdp1atWmVqDwAWFhawsLAoS2lERESkp8oURszNzeHr64vQ0FAMGjQIgGoAa2hoKKZNm1boOh07dkRoaChmzpypWXbkyBF07Nix1K+rHmPLsSNERET6Q/29XeK1MqKMdu3aJSwsLMTWrVvF5cuXxeTJk4Wjo6NITEwUQggxZswYMXfuXE37f/75R5iamorPPvtMXLlyRSxevFiYmZmJCxculPo14+LiBAA++OCDDz744EMPH3FxccV+z5f53jRBQUFITk7GokWLkJiYiFatWuHQoUOaQap37tyBicnToSidOnXCjh07sGDBAsyfPx8NGjTAvn370Lx581K/ppubG+Li4mBnZweZ+rbbFSAjIwOenp6Ii4szikuGjWl/ua+Gy5j2l/tquIxlf4UQyMzMhJubW7HtyjzPiCExtvlLjGl/ua+Gy5j2l/tquIxtf0uik1fTEBERkfFgGCEiIiJJGXUYsbCwwOLFi43mMmJj2l/uq+Eypv3lvhouY9vfkhj1mBEiIiKSnlH3jBAREZH0GEaIiIhIUgwjREREJCmGESIiIpIUwwgRERFJyuDDyLp16+Dt7Q1LS0v4+fkhMjKy2PY//vgjGjduDEtLS7Ro0QIHDx6sokpfTHBwMNq1awc7OzvUrFkTgwYNwrVr14pdZ+vWrZDJZFoPS0vLKqq4/N5///0CdTdu3LjYdfT1uHp7exfYV5lMhqlTpxbaXt+O6V9//YX+/fvDzc0NMpkM+/bt03peCIFFixbB1dUVVlZWCAgIwI0bN0rcblk/91WhuH198uQJ5syZgxYtWsDGxgZubm4YO3Ys7t27V+w2y/NZqAolHdfx48cXqLt3794lblcXjytQ8v4W9hmWyWRYvnx5kdvU1WNbWQw6jOzevRuzZs3C4sWLERUVBR8fH/Tq1Qv3798vtP3x48cxYsQITJw4EWfPnsWgQYMwaNAgXLx4sYorL7s///wTU6dOxYkTJ3DkyBE8efIEPXv2RFZWVrHr2dvbIyEhQfOIjY2toopfTLNmzbTq/vvvv4tsq8/H9dSpU1r7eeTIEQDA0KFDi1xHn45pVlYWfHx8sG7dukKfX7ZsGVavXo0NGzbg5MmTsLGxQa9evZCTk1PkNsv6ua8qxe1rdnY2oqKisHDhQkRFRSEkJATXrl3DgAEDStxuWT4LVaWk4woAvXv31qp7586dxW5TV48rUPL+PrufCQkJ2Lx5M2QyGQYPHlzsdnXx2Faast61V5+0b99eTJ06VfOzQqEQbm5uIjg4uND2w4YNE6+++qrWMj8/P/Hmm29Wap2V4f79+wKA+PPPP4tss2XLFuHg4FB1RVWQxYsXCx8fn1K3N6TjOmPGDFGvXj2hVCoLfV5fj6kQQgAQe/fu1fysVCpFrVq1xPLlyzXL0tLShIWFhdi5c2eR2ynr514Kz+9rYSIjIwUAERsbW2Sbsn4WpFDYvo4bN04MHDiwTNvRh+MqROmO7cCBA8XLL79cbBt9OLYVyWB7RvLy8nDmzBkEBARolpmYmCAgIAARERGFrhMREaHVHgB69epVZHtdlp6eDgCoXr16se0ePXoELy8veHp6YuDAgbh06VJVlPfCbty4ATc3N9StWxejRo3CnTt3imxrKMc1Ly8P27Ztw+uvv17s3av19Zg+Lzo6GomJiVrHzsHBAX5+fkUeu/J87nVVeno6ZDIZHB0di21Xls+CLgkPD0fNmjXRqFEjTJkyBampqUW2NaTjmpSUhF9//RUTJ04ssa2+HtvyMNgwkpKSAoVCARcXF63lLi4uSExMLHSdxMTEMrXXVUqlEjNnzkTnzp3RvHnzIts1atQImzdvxv79+7Ft2zYolUp06tQJd+/ercJqy87Pzw9bt27FoUOHsH79ekRHR8Pf3x+ZmZmFtjeU47pv3z6kpaVh/PjxRbbR12NaGPXxKcuxK8/nXhfl5ORgzpw5GDFiRLF3dC3rZ0FX9O7dG9999x1CQ0Px6aef4s8//0SfPn2gUCgKbW8oxxUAvv32W9jZ2SEwMLDYdvp6bMvLVOoCqOJNnToVFy9eLPH8YseOHdGxY0fNz506dUKTJk3w1Vdf4cMPP6zsMsutT58+mv9u2bIl/Pz84OXlhR9++KFUf23oq2+++QZ9+vSBm5tbkW309ZjSU0+ePMGwYcMghMD69euLbauvn4Xhw4dr/rtFixZo2bIl6tWrh/DwcLzyyisSVlb5Nm/ejFGjRpU4sFxfj215GWzPiJOTE+RyOZKSkrSWJyUloVatWoWuU6tWrTK110XTpk3DgQMHEBYWBg8PjzKta2ZmhtatW+PmzZuVVF3lcHR0RMOGDYus2xCOa2xsLI4ePYo33nijTOvp6zEFoDk+ZTl25fnc6xJ1EImNjcWRI0eK7RUpTEmfBV1Vt25dODk5FVm3vh9XtWPHjuHatWtl/hwD+ntsS8tgw4i5uTl8fX0RGhqqWaZUKhEaGqr1l+OzOnbsqNUeAI4cOVJke10ihMC0adOwd+9e/PHHH6hTp06Zt6FQKHDhwgW4urpWQoWV59GjR7h161aRdevzcVXbsmULatasiVdffbVM6+nrMQWAOnXqoFatWlrHLiMjAydPnizy2JXnc68r1EHkxo0bOHr0KGrUqFHmbZT0WdBVd+/eRWpqapF16/NxfdY333wDX19f+Pj4lHldfT22pSb1CNrKtGvXLmFhYSG2bt0qLl++LCZPniwcHR1FYmKiEEKIMWPGiLlz52ra//PPP8LU1FR89tln4sqVK2Lx4sXCzMxMXLhwQapdKLUpU6YIBwcHER4eLhISEjSP7OxsTZvn9/eDDz4Qhw8fFrdu3RJnzpwRw4cPF5aWluLSpUtS7EKpvffeeyI8PFxER0eLf/75RwQEBAgnJydx//59IYRhHVchVFcN1K5dW8yZM6fAc/p+TDMzM8XZs2fF2bNnBQCxYsUKcfbsWc0VJJ988olwdHQU+/fvF+fPnxcDBw4UderUEY8fP9Zs4+WXXxZr1qzR/FzS514qxe1rXl6eGDBggPDw8BDnzp3T+gzn5uZqtvH8vpb0WZBKcfuamZkpZs+eLSIiIkR0dLQ4evSoaNOmjWjQoIHIycnRbENfjqsQJf8eCyFEenq6sLa2FuvXry90G/pybCuLQYcRIYRYs2aNqF27tjA3Nxft27cXJ06c0DzXtWtXMW7cOK32P/zwg2jYsKEwNzcXzZo1E7/++msVV1w+AAp9bNmyRdPm+f2dOXOm5r1xcXERffv2FVFRUVVffBkFBQUJV1dXYW5uLtzd3UVQUJC4efOm5nlDOq5CCHH48GEBQFy7dq3Ac/p+TMPCwgr9vVXvk1KpFAsXLhQuLi7CwsJCvPLKKwXeBy8vL7F48WKtZcV97qVS3L5GR0cX+RkOCwvTbOP5fS3psyCV4vY1Oztb9OzZUzg7OwszMzPh5eUlJk2aVCBU6MtxFaLk32MhhPjqq6+ElZWVSEtLK3Qb+nJsK4tMCCEqteuFiIiIqBgGO2aEiIiI9APDCBEREUmKYYSIiIgkxTBCREREkmIYISIiIkkxjBAREZGkGEaIiIhIUgwjREREJCmGESIiIpIUwwgRERFJimGEiIiIJPX/AfcIT3E4PeCSAAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"np.random.seed(42) # Setting a fixed start Value for the Generator\n",
|
||
"pcgs: np.array = None\n",
|
||
"pcgs_sorted: np.array = None\n",
|
||
"\n",
|
||
"# BEGIN SOLUTION\n",
|
||
"gen = np.random.default_rng()\n",
|
||
"pcgs = np.array([gen.random() for _ in range(20)])\n",
|
||
"pcgs_sorted = np.sort(pcgs)\n",
|
||
"\n",
|
||
"# Plot\n",
|
||
"plt.scatter(np.arange(len(pcgs_sorted)), pcgs, color='r', label='PCGs')\n",
|
||
"plt.plot(np.arange(len(pcgs_sorted)), pcgs_sorted, color='g', label='Sortierte PCGs')\n",
|
||
"plt.title(\"PCG Random Numbers\")\n",
|
||
"plt.legend()\n",
|
||
"plt.show()\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "81f765b9-5a70-4c5f-93bc-b06ee655b3a5",
|
||
"metadata": {},
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 42,
|
||
"id": "91d763ff-71ac-4940-9cf8-54ca7ea6b8ca",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-69197dfdc3015ec5",
|
||
"locked": true,
|
||
"points": 3,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"PCGs [0.39787148 0.93848582 0.15923912 0.11887978 0.28188342 0.0065017\n",
|
||
" 0.54349094 0.76825107 0.12562835 0.03294871 0.82149947 0.07167748\n",
|
||
" 0.46462778 0.710785 0.06627364 0.13104628 0.77441648 0.69096057\n",
|
||
" 0.26849046 0.8829005 ]\n",
|
||
"Sorted PCGs [0.0065017 0.03294871 0.06627364 0.07167748 0.11887978 0.12562835\n",
|
||
" 0.13104628 0.15923912 0.26849046 0.28188342 0.39787148 0.46462778\n",
|
||
" 0.54349094 0.69096057 0.710785 0.76825107 0.77441648 0.82149947\n",
|
||
" 0.8829005 0.93848582]\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"# Hier werden ihre Lösungen getestet ...\n",
|
||
"print(\"PCGs\", pcgs)\n",
|
||
"print(\"Sorted PCGs\", pcgs_sorted)\n",
|
||
"### BEGIN HIDDEN TESTS\n",
|
||
"np.random.seed(42)\n",
|
||
"test_gen = np.random.default_rng()\n",
|
||
"test_pcgs = np.array([gen.random() for _ in range(20)])\n",
|
||
"test_pcgs_sorted = np.sort(pcgs)\n",
|
||
"### END HIDDEN TESTS\n",
|
||
"\n",
|
||
"# Check if pcgs are correctly generated\n",
|
||
"assert test_pcgs.all() == pcgs.all()\n",
|
||
"\n",
|
||
"# Check if pcgs are correctly sorted\n",
|
||
"assert test_pcgs_sorted.all() == pcgs_sorted.all()\n",
|
||
"\n",
|
||
"# Plot is manually checked"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "9283cd7a-b8a6-4090-84c3-da70e61b2d2e",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-486bea96505ad0a6",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"---\n",
|
||
"\n",
|
||
"# Plot Types\n",
|
||
"\n",
|
||
"Im folgenden Kapitel beschäftigen wir uns mit verschiedenen **Plot-Typen** und deren Einsatzmöglichkeiten, um Daten auf unterschiedliche Weise anschaulich darzustellen."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "8fe0a0f7-a836-4279-bc7c-e993004f97aa",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-79e43d78c9874975",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Line Plots\n",
|
||
"\n",
|
||
"Line Plots haben wir im vorherigen Kapitel bereits kennengelernt. Sie werden mithilfe von `plt.plot` erstellt und eignen sich besonders gut, um den Verlauf von Daten über eine kontinuierliche Skala darzustellen. \n",
|
||
"\n",
|
||
"Beispiel: Sinus-Funktion"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 43,
|
||
"id": "19b25d9b-0ee5-4eff-b290-8513f7948f50",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-b48b1eec8fe65537",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAWWhJREFUeJzt3XlYVPXiBvD3zADDvskum4iKpoKiEi5lSaKZZVlpV0PN9GZqmd5K7q+022b7Lc2raa5l2WqZ3VDDLRVFUVxwRUE22URm2JeZ8/sDnOK6gTJ8Z3k/z3Oeex3OHN5Bc17PfBdJlmUZRERERGZEIToAERERUWtjwSEiIiKzw4JDREREZocFh4iIiMwOCw4RERGZHRYcIiIiMjssOERERGR2WHCIiIjI7FiJDiCCTqdDXl4enJycIEmS6DhERETUDLIso6ysDH5+flAobnyPxiILTl5eHgICAkTHICIioluQnZ0Nf3//G55jkQXHyckJQMMPyNnZWXAaIiIiag6NRoOAgAD9+/iNWGTBufKxlLOzMwsOERGRiWnO8BIOMiYiIiKzw4JDREREZocFh4iIiMwOCw4RERGZHRYcIiIiMjssOERERGR2WHCIiIjI7LDgEBERkdlhwSEiIiKzY9CCs2vXLowcORJ+fn6QJAk//fTTTZ+zY8cO9O7dGyqVCqGhoVi9evVV5yxevBjBwcGwtbVFVFQUkpOTWz88ERERmSyDFpyKigqEh4dj8eLFzTo/IyMDI0aMwD333IPU1FTMmjULTz/9NDZv3qw/55tvvsHs2bMxf/58HDp0COHh4YiNjUVhYaGhXgYRERGZGEmWZblNvpEkYcOGDRg1atR1z3n55Zfx66+/4vjx4/rHxo4di9LSUiQkJAAAoqKi0LdvX3z66acAAJ1Oh4CAAMycORNz585tVhaNRgMXFxeo1WruRUVERGQiWvL+bVSbbSYlJSEmJqbJY7GxsZg1axYAoLa2FikpKYiPj9d/XaFQICYmBklJSde9bk1NDWpqavS/1mg0rRucTFJ1nRYZxRXIKK5AUVkNLpXXoKZehzqtDGsrCU4qK7ja28DfzQ6B7vYIaucApeLmG7wREZF4RlVw8vPz4e3t3eQxb29vaDQaVFVV4fLly9Bqtdc859SpU9e97oIFC/Cvf/3LIJnJdFTU1GPXmSIknb+E5IwSnCkog64F9y8dbJS4o70L+gW7467OnugV6AprJcfpExEZI6MqOIYSHx+P2bNn63+t0WgQEBAgMBG1lZp6LbaeKMCGQ7n4I70YtfW6Jl93srVCqJcjfJxt4eGogp2NEkqFhLp6Hcpr6lFcXoucy5XIvFSBilotkjNKkJxRgk+3p8PV3hrDu/tiVIQf+nVwhyTx7g4RkbEwqoLj4+ODgoKCJo8VFBTA2dkZdnZ2UCqVUCqV1zzHx8fnutdVqVRQqVQGyUzGqVBTjZV7MvHNgSxcrqzTPx7czh6Du3ihb7A7ege5wsfZtlnFRKuTca6oHKlZpdidXozd6cUoqajF18lZ+Do5C528HBEXHYTRkf6wtzGq/6yIiCySUf1NHB0djf/+979NHtu6dSuio6MBADY2NoiMjERiYqJ+sLJOp0NiYiJmzJjR1nHJCF1UV2FhYjp+SMlBrbbhbo2Psy1GR7bHQxHt0cnL8ZbutCgVEjp7O6GztxMe7xsArU7G/vOX8HNqHjYdzcPZwnK8+nMaPv79LKbeFYLxdwbBQWVU/3kREVkUg/4NXF5ejvT0dP2vMzIykJqaCnd3dwQGBiI+Ph65ublYu3YtAOCZZ57Bp59+ipdeeglPPfUUtm3bhm+//Ra//vqr/hqzZ8/GhAkT0KdPH/Tr1w8ff/wxKioqMGnSJEO+FDJyZdV1+HRbOlbvzURN48dQfYLcMOWuEMR09W71wcFKhYT+oR7oH+qB/3ugK35MycGKPRnILqnCgt9O4fPdGXgxtgse7e0PBQcmExG1OYNOE9+xYwfuueeeqx6fMGECVq9ejYkTJyIzMxM7duxo8pwXXngBJ06cgL+/P1599VVMnDixyfM//fRTvP/++8jPz0dERAQWLlyIqKioZufiNHHzIcsyNh7Jw5u/nkRRWcNMuX7B7vhHbBf06+DeplnqtDr8dDgXC7edRXZJFQCge3tnvPNIT3Rv79KmWYiIzFFL3r/bbB0cY8KCYx7y1dWY++NR7DhdBKBhfM28kd1wTxcvoQN+a+q1WLM3E4sS01FWUw+lQsLkgR0w+77OsLVWCstFRGTqWHBuggXH9P2cmotXfjqOsup62FgpMPOeUEy9OwQqK+MpEEVlNfjXL2nYdPQiAKCztyM+HtML3fz4Z46I6Faw4NwEC47pqqrV4rWNafjmYDYAINzfBR88Fo5O3k6Ck13f7ycKMPfHYygur4GNUoH/G9EVcdFBnFZORNRCLDg3wYJjmrIuVWLK2oM4XVAGSQJm3hOK54Z0gpUJLLZXXF6DuT8cxe8nG/ZMGxXhh7cf6cEp5URELdCS92/jf2cgArAnvRgPLt6N0wVl8HBUYd3kKMwe2sUkyg0AeDiqsDyuD14Z0RVKhYSfUvPwyH/2Ire0SnQ0IiKzZBrvDmTR1idnIW5lMkor6xAe4IpfnxuI/qEeomO1mCRJeHpQCL56Ogoejiqcyi/DqMV7cCS7VHQ0IiKzw4JDRkuWZXy09Qzm/ngMWp2MR3q1xzdT74S3s63oaLclKqQdfpreH2E+Tigqq8GYZUnYdqrg5k8kIqJmY8Eho6TVyfjnhmNYmHgWAPDckE748PFws5lm7e9mj++eicbgLp6ortNhytoU/HgoR3QsIiKzwYJDRqdOq8Psb1PxdXI2FBKw4JEemH1fZ7ObdeRka43lcX3wcK/20OpkzP72CL7cd0F0LCIis8ApHGRU6rQ6zPzqMBLS8mGlkPDJ2F4Y0dNXdCyDsVYq8OFj4XC1t8aqPZl45afjsFJIGNsvUHQ0IiKTxoJDRkOrk/GP744gIS0fNlYKLB3fG/eGeYuOZXAKhYR5D3SDBAkr92QgfsMxKBUSHusTIDoaEZHJ4kdUZBRkWcYrPx3Dz6l5sFJIWDLOMsrNFZIk4dUHumJCdBBkGXjph6PYcJhjcoiIbhULDgknyzLe/PWkfszNv8dEYEhXyyk3V0iShNcevAPjogIhy8Ccb49g45E80bGIiEwSCw4J9+/fz2LF7gwAwDuje2JkuJ/gROJIkoQ3HuqOsX0DoJOB2d+kYvfZYtGxiIhMDgsOCfVFUqZ+KvhrI7vhcY47gUIh4e2He+DBcD/U62RM+zIFp/PLRMciIjIpLDgkzM4zRXjtlxMAgDn3dcbEAR0EJzIeCoWE9x/riX7B7iirqcekVcko0FSLjkVEZDJYcEiIMwVlmLHuELQ6GaN7+2PGvaGiIxkdlZUSy+IiEeLpgDx1NZ5afQAVNfWiYxERmQQWHGpzxeU1eGr1AZTV1KNfB3cseKSH2S3i11pc7W2wemI/tHOwQVqeBjO+OoR6rU50LCIio8eCQ22quk6LqWsPIudyFYLa2eOz8ZGwseIfwxsJbGePFRP7wtZage2ni/D2f0+JjkREZPT4zkJtRpZlxP94DIeySuFsa4WVE/vCzcFGdCyTEBHgio/HRAAAVu7J4PRxIqKbYMGhNvPlvgvYcDgXSoWEJeMj0dHTUXQkkzKsuy+eHdwRAPDy90c5s4qI6AZYcKhNpGaX4vVNDTOm4oeHYUCoh+BEpmnO0C4YGOqBqjotnvkyBZrqOtGRiIiMEgsOGdzlilpMX3cIdVoZsXd4Y/JATge/VUqFhIVP9EJ7VztkFFdgzrdHoNPJomMRERkdFhwyKJ1OxuxvU5Fb2jCo+P3Hwjlj6ja5O9hgyfjesLFSYOuJAizZeU50JCIio8OCQwa1ZOc5bD9dBJWVAv8Z1xvOttaiI5mFnv6ueOOhOwAAH245jeSMEsGJiIiMCwsOGcy+85fw4ZbTAIA3HuqOO/xcBCcyL2P6BmJ0b3/oZOCFb1KhruJ4HCKiK1hwyCDUVXWY/U0qdDIwurc/Hu/LPaYM4V8P3YGgdvbILa3C/204BlnmeBwiIoAFhwxk3s/HkaeuRlA7e7ze+FEKtT5HlRU+GdsLVgoJm45exA+HckVHIiIyCiw41Op+Ts3Fz6l5UCok/HtMBBxUVqIjmbWIAFe8cF9nAA3FMrO4QnAiIiLxWHCoVeWVVuGVn44DAGbcE4regW6CE1mGZ+7uiKgO7qis1eL59YdRx/2qiMjCseBQq9HpZMz59gjKqusREeDKHcLb0JW7Zc62VjiSo8aixLOiIxERCcWCQ61mxe4MJJ2/BDtrJf49JgLWSv7xakt+rnZ4+5EeAIDFO87heK5acCIiInHa5B1o8eLFCA4Ohq2tLaKiopCcnHzdcwcPHgxJkq46RowYoT9n4sSJV3192LBhbfFS6DrSC8vxfuOU8Hkju6GDh4PgRJbpgZ5+uL+HD7Q6GS9+fxS19fyoiogsk8ELzjfffIPZs2dj/vz5OHToEMLDwxEbG4vCwsJrnv/jjz/i4sWL+uP48eNQKpV47LHHmpw3bNiwJud9/fXXhn4pdB06nYy5PzS8md7d2RNjOSVcqNcf6g43e2ucvKjBkh1c5ZiILJPBC85HH32EKVOmYNKkSejWrRuWLl0Ke3t7rFy58prnu7u7w8fHR39s3boV9vb2VxUclUrV5Dw3Nw5mFeWLfRdw8MJlONgo8fYjPbgVg2Aejiq89mDD1PxF287i5EWN4ERERG3PoAWntrYWKSkpiImJ+fMbKhSIiYlBUlJSs66xYsUKjB07Fg4OTT/y2LFjB7y8vNClSxdMmzYNly5duu41ampqoNFomhzUOnIuV+LdhFMAgLnDw9De1U5wIgKAB8P9cF83b9TrZLz4/RHOqiIii2PQglNcXAytVgtvb+8mj3t7eyM/P/+mz09OTsbx48fx9NNPN3l82LBhWLt2LRITE/Huu+9i586dGD58OLRa7TWvs2DBAri4uOiPgAB+hNIaZFnGPzccR2WtFn2D3TAuKkh0JGokSRLeGtUdLnbWOJ6rwbJd50VHIiJqU0Y9zWXFihXo0aMH+vXr1+TxsWPH4sEHH0SPHj0watQobNq0CQcOHMCOHTuueZ34+Hio1Wr9kZ2d3Qbpzd8Ph3Kx60wRbKwUeGd0TygU/GjKmHg522L+yG4AgE9+P4tzReWCExERtR2DFhwPDw8olUoUFBQ0ebygoAA+Pj43fG5FRQXWr1+PyZMn3/T7hISEwMPDA+np6df8ukqlgrOzc5ODbk9hWTXe2HQCADArphM6ejoKTkTX8nCv9hjcxRO1Wh1e/ek496oiIoth0IJjY2ODyMhIJCYm6h/T6XRITExEdHT0DZ/73XffoaamBuPHj7/p98nJycGlS5fg6+t725mped7cdBLqqjrc4eeMKYNCRMeh65AkCa8/2B0qKwX2nruEn1PzREciImoTBv+Iavbs2Vi+fDnWrFmDkydPYtq0aaioqMCkSZMAAHFxcYiPj7/qeStWrMCoUaPQrl27Jo+Xl5fjxRdfxL59+5CZmYnExEQ89NBDCA0NRWxsrKFfDgHYm16MjUfyIEnAO4/05IJ+Ri6wnT2eG9IJAPDmryegrqwTnIiIyPAMvgvimDFjUFRUhHnz5iE/Px8RERFISEjQDzzOysqCQtH0DfL06dPYvXs3tmzZctX1lEoljh49ijVr1qC0tBR+fn4YOnQo3njjDahUKkO/HItXW6/Dqz837DU1PioIPfxdBCei5pgyKAQbDucivbAc720+hbce7iE6EhGRQUmyBX4or9Fo4OLiArVazfE4LbRkxzm8m3AK7RxssG3OYLjYW4uORM207/wljF22D5IE/DCtPzdCJSKT05L3b362QM2WW1qFhY2bOP7z/q4sNybmzpB2eKR3e8gy8H8bjqOea+MQkRljwaFme/2XNFTVadEv2B2P9G4vOg7dgn/e3xUudg3bOKxJuiA6DhGRwbDgULNsP12IzWkFUCokvD7qDm7HYKI8HFV4eVgYAODj38+guLxGcCIiIsNgwaGbqqnX4rWNaQCASf2DEebDcUumbEzfAHRv74yy6np82LgDPBGRuWHBoZtatScTFy5VwstJhVn3dRYdh26TUiFh/siGzTjXH8jG8Vy14ERERK2PBYduqKisBp9ua1gh+qVhYXBUGXxlAWoDfYPdMTLcD7IM/OuXNK5wTERmhwWHbujDLadRXlOPnv4ueKQXBxabk/jhYbC1VuBA5mVsOnpRdBwiolbFgkPXlZanxjcHGzYmnfdAN26maWb8XO0w7e5QAMCC/55EVa1WcCIiotbDgkPXJMsyXv/lBGQZeKCnL/oEu4uORAbw97tD0N7VDnnqaizdeU50HCKiVsOCQ9e0Oa0A+zNKoLJSYO7wMNFxyEBsrZX45/1dAQBLd55DXmmV4ERERK2DBYeuUlOvxdv/PQkAmHpXCPzd7AUnIkO6v4cP+gW7o6Zehw+3nBEdh4ioVbDg0FVW78lEVknDtPBn7u4oOg4ZmCRJ+OeIhrs4Px7OwYk8jeBERES3jwWHmiitrMXi7Q3Twl+M7QIHTgu3CBEBrnigpy9kGVjw20nRcYiIbhsLDjXxnx3noKmuR5iPEx7p7S86DrWhl2LDYK2U8MfZYuw6UyQ6DhHRbWHBIb3c0iqs3psJAHh5WBiUnBZuUQLb2ePJO4MBAAt+OwWtjov/EZHpYsEhvQ+3nEZtvQ53hrhjcBdP0XFIgJn3hsLJ1gonL2qw4XCu6DhERLeMBYcAACfy/nxDix/elbuFWyg3BxtMv6dh8b8Pt5xGdR0X/yMi08SCQwCA9zafgiwDI3r6IjzAVXQcEmhi/2C0d7XDRXU1Vu7JEB2HiOiWsOAQ9p4rxo7TRbBSSHhxaBfRcUgwW2sl5gxt2DV+6Y5zUFfWCU5ERNRyLDgWTpZlvPPbKQDAuKhABHs4CE5ExuChiPbo4u0ETXU9lv3BLRyIyPSw4Fi4zWn5OJqjhoONEjOHdBIdh4yEUiHp7+Ks3J2JorIawYmIiFqGBceCaXWyfmn+yQM7wMNRJTgRGZP7unkjPMAVVXVa/eKPRESmggXHgv1yJA9nC8vhbGuFyYNCRMchIyNJf47J+mp/FnK5EScRmRAWHAtVp9Xh37833L35+90d4WJnLTgRGaMBoe0QHdIOtVodFv5+VnQcIqJmY8GxUD+k5ODCpUp4ONpg0oBg0XHISEmShH/ENtzF+f5QDs4VlQtORETUPCw4FqimXouFiQ3/Gp82OBT2NtxQk64vMsgNMV29oNXJ+PfWM6LjEBE1CwuOBfp6fxby1NXwcbbFuKhA0XHIBMxpHIuz6ehFnMjTCE5DRHRzLDgWpqpWi0+3N6xrMnNIKGytlYITkSno6uuMB3r6AgA+SeRdHCIyfiw4FmZtUiaKy2sQ6G6Px/sEiI5DJuT5IZ0gScDmtAKk5alFxyEiuiEWHAtSUVOPz3adBwA8N6QTrJX87afm6+TthAd6+gEAPuGMKiIycnyHsyBf7ruAkopaBLezx6gIP9FxyAQ9PyQUkgRsOVGA47m8i0NExqtNCs7ixYsRHBwMW1tbREVFITk5+brnrl69GpIkNTlsbW2bnCPLMubNmwdfX1/Y2dkhJiYGZ8/yX5Q3Ullbj2WNd29m3NsJVrx7Q7cg1MsJI6/cxUnkf3NEZLwM/i73zTffYPbs2Zg/fz4OHTqE8PBwxMbGorCw8LrPcXZ2xsWLF/XHhQsXmnz9vffew8KFC7F06VLs378fDg4OiI2NRXV1taFfjslaty8LlypqEcS7N3Sbnmsci7OVd3GIyIgZvOB89NFHmDJlCiZNmoRu3bph6dKlsLe3x8qVK6/7HEmS4OPjoz+8vb31X5NlGR9//DFeeeUVPPTQQ+jZsyfWrl2LvLw8/PTTT4Z+OSapqlaLz3Y1zJyafk8o797QbQn1csSD4Q0l+WOOxSEiI2XQd7ra2lqkpKQgJibmz2+oUCAmJgZJSUnXfV55eTmCgoIQEBCAhx56CGlpafqvZWRkID8/v8k1XVxcEBUVdd1r1tTUQKPRNDksybr9F1BcXosAdzs83Ku96DhkBmbe2wkKCfj9JO/iEJFxMmjBKS4uhlarbXIHBgC8vb2Rn59/zed06dIFK1euxM8//4wvv/wSOp0O/fv3R05ODgDon9eSay5YsAAuLi76IyDAcqZHV9VqsXRnw9ibmfdw5hS1Dt7FISJjZ3TvdtHR0YiLi0NERATuvvtu/Pjjj/D09MRnn312y9eMj4+HWq3WH9nZ2a2Y2Lh9lZyF4vKahrs3vXn3hlrPzMaxOL+fLMCpfMu6K0pExs+gBcfDwwNKpRIFBQVNHi8oKICPj0+zrmFtbY1evXohPT0dAPTPa8k1VSoVnJ2dmxyWoLpOi6U7G8feDA7l3RtqVR09HXF/j4bVjRc3ro5NRGQsDPqOZ2Njg8jISCQmJuof0+l0SExMRHR0dLOuodVqcezYMfj6NvxF2qFDB/j4+DS5pkajwf79+5t9TUvx3cFsFJXVoL2rHR7p7S86Dpmh6YNDAQC/Hs1DRnGF4DRERH8y+D/pZ8+ejeXLl2PNmjU4efIkpk2bhoqKCkyaNAkAEBcXh/j4eP35r7/+OrZs2YLz58/j0KFDGD9+PC5cuICnn34aQMMMq1mzZuHNN9/Exo0bcezYMcTFxcHPzw+jRo0y9MsxGXVanX7szTN3h8DGindvqPV183PGkDAv6GRgyY500XGIiPSsDP0NxowZg6KiIsybNw/5+fmIiIhAQkKCfpBwVlYWFIo/33wvX76MKVOmID8/H25uboiMjMTevXvRrVs3/TkvvfQSKioqMHXqVJSWlmLgwIFISEi4akFAS7YxNQ+5pVXwcFThMe45RQY0/d5QJJ4qxI+HcvF8TGe0d7UTHYmICJIsy7LoEG1No9HAxcUFarXaLMfj6HQy7vv3TpwrqsDc4WF45u6OoiORmXti2T4knb+ECdFB+NdD3UXHISIz1ZL3b35uYYa2nMjHuaIKONtaYVxUoOg4ZAFm3NswFmf9gYZxX0REorHgmBlZlvUzWib2D4aTrbXgRGQJ+ndsh4gAV9TU6/D57vOi4xARseCYmz/OFuNYrhp21kpMHNBBdByyEJIkYcY9DXdxvky6gNLKWsGJiMjSseCYmcXbG2ay/C0qEO4ONoLTkCUZ0tULYT5OqKjVYvXeTNFxiMjCseCYkYOZJdifUQJrpYQpg0JExyELI0kSpjfexVm1JxPlNfWCExGRJWPBMSP/2dEw9ubRSH/4uHDKPLW9+3v4IsTDAeqqOny1/4LoOERkwVhwzERanhrbThVCIQF/v4vTwkkMpULCM4Mb/vwt/yMD1XVawYmIyFKx4JiJJY13b0b09EOwh4PgNGTJHu7VHu1d7VBUVoPvDlrOxrZEZFxYcMzA+aJy/HrsIgDg2cG8e0NiWSsV+PvdDWPAlv+RgXqtTnAiIrJELDhm4LOd5yHLwJAwL3T1Nb+Vmcn0PBYZADd7a2SVVCIhLV90HCKyQCw4Ji5fXY0fD+cAAJ69h3dvyDjY2SgxoX8wgCsF3OJ2hCEiwVhwTNyqvRmo08roF+yOyCB30XGI9OKig2FrrcCxXDWSzl8SHYeILAwLjgkrq67DV/uyAABT7+K6N2Rc3B1s8HjjTvaf7eT2DUTUtlhwTNj65GyU1dSjo6cD7g3zEh2H6CpPDwyBQgJ2ninCyYsa0XGIyIKw4JioOq0OK/dkAGi4e6NQSIITEV0tsJ097u/hCwBYtot3cYio7bDgmKhfjuThoroank4qjOrVXnQcouu6svDkL0fykFtaJTgNEVkKFhwTJMuy/l/DE/sHQ2WlFJyI6Pp6+Lugf8d2qNfJWLk7Q3QcIrIQLDgmaNfZYpzKL4O9jRLjo4JExyG6qb/f3XAX5+vkLKgr6wSnISJLwIJjgpbtatiWYWzfQLjYWwtOQ3Rzd3XyQJiPEyprtfiSm3ASURtgwTExx3PV2JN+CUqFhKcGBouOQ9QskiTpt29YtSeTm3ASkcGx4JiYK2NvHujpC383e8FpiJrvgZ5+8HOxRXF5DTYczhUdh4jMHAuOCcm5XKnfVJML+5GpsVYqMHlQ4yacu85Dq+P2DURkOCw4JmTF7gxodTIGhnrgDj8X0XGIWmxs3wA421rhfHEFtp4oEB2HiMwYC46JUFfW4ZsD2QB494ZMl4PKCuPvbJj5xynjRGRILDgm4sv9F1BZq0VXX2cM6uQhOg7RLZvQPxjWSgnJmSU4kl0qOg4RmSkWHBNQU6/F6r2ZAICpd3WAJHFbBjJd3s62GNnTD0DDx65ERIbAgmMCNh25iKKyGvg42+KBxjcGIlP21MAOAIBfj11EHrdvICIDYMExcrIs6/+VG9c/CNZK/paR6eve3gXRIe2g1clY03h3koioNfHd0sjtO1+CExc1sLVW4G/9AkXHIWo1Tw9quIvzVXIWymvqBachInPDgmPkrty9Gd3bH672NoLTELWee7p4IcTDAWXV9fjuYLboOERkZlhwjFhmcQUSTzWsFXJlzAKRuVAoJP2f65V7MrjwHxG1qjYpOIsXL0ZwcDBsbW0RFRWF5OTk6567fPlyDBo0CG5ubnBzc0NMTMxV50+cOBGSJDU5hg0bZuiX0eZW7cmALAP3dPFER09H0XGIWl3DnUlrZJdUYeuJfNFxiMiMGLzgfPPNN5g9ezbmz5+PQ4cOITw8HLGxsSgsLLzm+Tt27MATTzyB7du3IykpCQEBARg6dChyc5vuXTNs2DBcvHhRf3z99deGfiltSl1Vh+9ScgAAkwdyYT8yT3Y2SoyPalj47/M/OGWciFqPwQvORx99hClTpmDSpEno1q0bli5dCnt7e6xcufKa569btw7PPvssIiIiEBYWhs8//xw6nQ6JiYlNzlOpVPDx8dEfbm5uhn4pbWp9chYqa7UI83HCgNB2ouMQGUxcdBCslRIOXriMw1mXRcchIjNh0IJTW1uLlJQUxMTE/PkNFQrExMQgKSmpWdeorKxEXV0d3N3dmzy+Y8cOeHl5oUuXLpg2bRouXbp03WvU1NRAo9E0OYxZvVannzr71AAu7EfmzcvZFiPDufAfEbUugxac4uJiaLVaeHt7N3nc29sb+fnN+7z95Zdfhp+fX5OSNGzYMKxduxaJiYl49913sXPnTgwfPhxarfaa11iwYAFcXFz0R0BAwK2/qDbw2/F85Kmr4eFogwcjuLAfmb/JjYONfzuej5zLlYLTEJE5MOpZVO+88w7Wr1+PDRs2wNbWVv/42LFj8eCDD6JHjx4YNWoUNm3ahAMHDmDHjh3XvE58fDzUarX+yM427impV/4VOy4qCLbWSsFpiAzvDj8X9O/Ihf+IqPUYtOB4eHhAqVSioKCgyeMFBQXw8fG54XM/+OADvPPOO9iyZQt69ux5w3NDQkLg4eGB9PT0a35dpVLB2dm5yWGsUi5cRmp2KWyUCv2uy0SW4MrCf+uTs1FWXSc4DRGZOoMWHBsbG0RGRjYZIHxlwHB0dPR1n/fee+/hjTfeQEJCAvr06XPT75OTk4NLly7B19e3VXKLtLLx7s1DEX7wdFIJTkPUdgZ39kKIpwPKaurxfeMMQiKiW2Xwj6hmz56N5cuXY82aNTh58iSmTZuGiooKTJo0CQAQFxeH+Ph4/fnvvvsuXn31VaxcuRLBwcHIz89Hfn4+ysvLAQDl5eV48cUXsW/fPmRmZiIxMREPPfQQQkNDERsba+iXY1A5lyvx2/GLAIDJg7iwH1kWhULCpP7BAIA1ezOh48J/RHQbDF5wxowZgw8++ADz5s1DREQEUlNTkZCQoB94nJWVhYsXL+rPX7JkCWpra/Hoo4/C19dXf3zwwQcAAKVSiaNHj+LBBx9E586dMXnyZERGRuKPP/6ASmXadzzW7M2ETgYGhLZDmI/xfoxGZCiP9PaHk60VMi9VYvvpa6+VRUTUHJIsyxb3zySNRgMXFxeo1WqjGY9TXlOP6LcTUVZTj5UT++DeMO+bP4nIDL316wks/yMDA0M98OXTUaLjEJERacn7t1HPorIk3x3MRllNPUI8HTC4s5foOETCxEUHQyEBu9OLcaagTHQcIjJRLDhGQKuTsWpPJgBg0oAOUCi4sB9ZrgB3e9zXreEO5pX/LoiIWooFxwj8frIAWSWVcLGzxuje7UXHIRJu0oCGQfYbDuegtLJWcBoiMkUsOEbgysJ+f4sKhL2NleA0ROJFdXBHN19nVNfp8HWycS/MSUTGiQVHsLQ8NZIzSqBUSIiL5sJ+RAAgSRImDQgGAHyRlIl6rU5sICIyOSw4gl1Zln54dx/4utiJDUNkREaG+6Gdgw3y1NXYnFZw8ycQEf0FC45AJRW1+Ck1DwD0/1ologa21kqMiwoEAKzcw13GiahlWHAE+jo5C7X1OvRo74LegW6i4xAZnfF3BsFaKSHlwmUczSkVHYeITAgLjiB1Wh2+3HcBADCxfzAkiVPDif6Xl7MtRvRo2GOOU8aJqCVYcATZklaAi+pqeDja4IFw098klMhQrkwZ33Q0D4WaasFpiMhUsOAIsnpv49TwfoFQWSkFpyEyXuEBrugd6Io6rYwv92eJjkNEJoIFR4DjuWocyLwMK4WEcXdyajjRzTw1sOEuzlf7L6CmXis4DRGZAhYcAVY3Tg2/v4cvvJ1txYYhMgGxd/jA18UWxeW1+OXIRdFxiMgEsOC0seLyGmxsnBo+kVPDiZrFWqnAk40LYa7akwFZlgUnIiJjx4LTxtYnZ6FWq0O4vwt6BbiKjkNkMp7oGwhbawXS8jQ4kHlZdBwiMnIsOG2oTqvDF1emhg/g1HCilnBzsMHDvRo2o13Fhf+I6CZYcNpQwvF8FGhq4OGowv09ODWcqKUm9m8YbLw5LR85lysFpyEiY8aC04auDC4eF8Wp4US3oouPEwaEtoNOhv5uKBHRtbDgtJGjOaVIuXAZ1kpJv78OEbXcpMa7OOuTs1FVyynjRHRtLDht5MrdmxE9fOHFqeFEt+yeMC8EuttDXVWHn1JzRcchIiPFgtMGispqsKlx7Y6JjcvOE9GtUSokxDVOGV+9J5NTxonomlhw2sDXjVPDIwJcEcGp4US37bE+AbC3UeJ0QRmSzl8SHYeIjBALjoHV1v+5a/gkLuxH1Cpc7Kwxurc/AO4yTkTXxoJjYL8dv4jCshp4OqkwvDunhhO1lgn9Gz6m+v1kAbJLOGWciJpiwTGwK4OLx0cFwcaKP26i1hLq5YRBnTwgy8DapEzRcYjIyPAd14BSs0txOKsU1koJf+PUcKJWd+Vj3/UHslFRUy82DBEZFRYcA1rTePdmZE8/eDqpxIYhMkODO3shuJ09yqrrseEwp4wT0Z9YcAyksKwam4427Bo+oX+w2DBEZkqhkPT/fa3eyynjRPQnFhwD+Wp/Fuq0MnoHuiKcU8OJDObRSH842CiRXliOPemcMk5EDVhwDKBhangWAC7sR2RoTrbWeKxPAABg9V7uMk5EDVhwDOC/xy6iuLwG3s4qDO/uIzoOkdm7srJx4qlCXLhUITgNERmDNik4ixcvRnBwMGxtbREVFYXk5OQbnv/dd98hLCwMtra26NGjB/773/82+bosy5g3bx58fX1hZ2eHmJgYnD171pAvoUVW/WVquLWSHZLI0EI8HTG4iydkGVizl7uME1EbFJxvvvkGs2fPxvz583Ho0CGEh4cjNjYWhYWF1zx/7969eOKJJzB58mQcPnwYo0aNwqhRo3D8+HH9Oe+99x4WLlyIpUuXYv/+/XBwcEBsbCyqq6sN/XJu6nDWZRzJLoWNUoEnODWcqM1MbBxs/N3BbJRzyjiRxZNkA087iIqKQt++ffHpp58CAHQ6HQICAjBz5kzMnTv3qvPHjBmDiooKbNq0Sf/YnXfeiYiICCxduhSyLMPPzw9z5szBP/7xDwCAWq2Gt7c3Vq9ejbFjx940k0ajgYuLC9RqNZydnVvplTZ4fv1h/Jyah9G9/fHh4+Gtem0iuj6dTkbMRztxvrgCrz90B+Kig0VHIqJW1pL3b4PewamtrUVKSgpiYmL+/IYKBWJiYpCUlHTN5yQlJTU5HwBiY2P152dkZCA/P7/JOS4uLoiKirruNWtqaqDRaJochlCgqcavRxt3DefUcKI2pVBImNi48N/qvZnQ6ThlnEiEMwVl+PsXB7FP8Ea4Bi04xcXF0Gq18Pb2bvK4t7c38vPzr/mc/Pz8G55/5X9bcs0FCxbAxcVFfwQEBNzS67mZdfuzUK+T0SfIDT38XQzyPYjo+h7p7Q8nlRXOF1Xgj/Ri0XGILNLqvZnYnFagX+xWFIsYARsfHw+1Wq0/srOzDfJ9Hu3tj6cHdsDUu0IMcn0iujFHldWfU8b3cMo4UVtTV9Zhw6GGVcVFL3Jr0ILj4eEBpVKJgoKCJo8XFBTAx+fa06d9fHxueP6V/23JNVUqFZydnZschhDYzh6vPNANQ+/g1HAiUeKigyBJwPbTRThfVC46DpFF+fZgNqrqtAjzcUJUB3ehWQxacGxsbBAZGYnExET9YzqdDomJiYiOjr7mc6Kjo5ucDwBbt27Vn9+hQwf4+Pg0OUej0WD//v3XvSYRWY5gDwfc28ULALA2iVPGidqKVidjTVImgIaNcCVJEprH4B9RzZ49G8uXL8eaNWtw8uRJTJs2DRUVFZg0aRIAIC4uDvHx8frzn3/+eSQkJODDDz/EqVOn8Nprr+HgwYOYMWMGAECSJMyaNQtvvvkmNm7ciGPHjiEuLg5+fn4YNWqUoV8OEZmAK4ONvzuYjbLqOrFhiCxE4skC5Fyugqu9NR6KaC86DqwM/Q3GjBmDoqIizJs3D/n5+YiIiEBCQoJ+kHBWVhYUij97Vv/+/fHVV1/hlVdewT//+U906tQJP/30E7p3764/56WXXkJFRQWmTp2K0tJSDBw4EAkJCbC1tTX0yyEiEzAw1AOhXo5ILyzH9yk5mMQtU4gM7srdm7F9A2FrrRQbBm2wDo4xMuQ6OERkHL7YdwGv/nQcwe3ssW3OYCgUYm+XE5mzMwVlGPrvXVBIwB8v34v2rnYG+T5Gsw4OEZEoo3u3h5OtFTIvVWLnmSLRcYjM2urGKeFDu/kYrNy0FAsOEZklexsrjO3bMGV8leD1OIjM2V+nhl8Z/2YMWHCIyGzFRQdDkoBdZ4qQXsgp40SGYExTw/+KBYeIzFaAuz1iujZMaBC9qiqROfrr1PCJ/cVPDf8rFhwiMmuTGldT/eFQDtRVnDJO1Jq2nSo0qqnhf8WCQ0RmLbpjO3T2dkRlrRbfHTTMNi1Elmr13oYtUcb0DYCdjfip4X/FgkNEZk2SJEzs37AOztqkC9Byl3GiVnGmoAx70i9BIQFP3hkkOs5VWHCIyOyN6uUHFztrZJVUYvupQtFxiMzCmr9MDfd3sxcb5hpYcIjI7P11yvhqDjYmum3qyjr8aCS7hl8PCw4RWYQno4OgkIDd6cU4W1AmOg6RSfsu5c+p4XeGGM/U8L9iwSEii+DvZo+h3XwAcOE/otvx16nhE4xsavhfseAQkcW4ssrqj4dyoK7klHGiW7HtVCGyS6rgYmeNUUY2NfyvWHCIyGJEdXBHmI8Tqut0+OZglug4RCbpyuDisf2Mb2r4X7HgEJHFkCQJkxrv4qzZyynjRC11tqAMu9OLjXZq+F+x4BCRRXkooj1c7a2RW1qF308WiI5DZFKuzEK8r5u3UU4N/ysWHCKyKLbWSjzRLxAAsHpPptgwRCaktLIWPxzKAQD94pnGjAWHiCzOk3cGQamQkHT+Ek7la0THITIJ6w9ko7pOh66+zkY7NfyvWHCIyOL4udph2B0NU8Z5F4fo5uq1Oqxt/Hhq0gDjnRr+Vyw4RGSRrkwZ33A4F5crasWGITJym9MKkKeuRjsHGzwY7ic6TrOw4BCRReoT5IY7/JxRU6/D+gPcZZzoRlbtadg1fFxUIGytjXdq+F+x4BCRRWrYZTwYAPBFUibqtTqxgYiM1NGcUhy8cBnWSgnjjXxq+F+x4BCRxRoZ7gd3Bxvkqaux9QSnjBNdy6rGcWoP9PSDl7Ot2DAtwIJDRBbL1lqJvzVOGef+VERXK9RUY9PRPADQL5JpKlhwiMiijW+cMp6cUYK0PLXoOERG5ct9F1CnlREZ5Iae/q6i47QICw4RWTQfF1sM794wZXwN7+IQ6VXXabFuf8OebU8NMP6F/f4XCw4RWbxJjX95/5Sah0vlNYLTEBmHjUfycKmiFn4utoi9w1t0nBZjwSEii9c70BU9/V1QyynjRAAAWZb1g4vj+gfDSml6dcH0EhMRtbKmU8YvoI5TxsnC7c8owcmLGthaKzC2b4DoOLeEBYeICMCInr7wcLRBvqYam9PyRcchEmrl7oaF/R7p7Q9XexvBaW4NCw4REQCVlRJ/i2pYxIz7U5Ely7pUia0nG9aFmtR4Z9MUseAQETUaHxUIK4WEgxcu41gOp4yTZVqTlAlZBgZ18kAnbyfRcW6ZQQtOSUkJxo0bB2dnZ7i6umLy5MkoLy+/4fkzZ85Ely5dYGdnh8DAQDz33HNQq5v+RSNJ0lXH+vXrDflSiMgCeDnbYkRPXwDAak4ZJwtUXlOPbxsH2j810PSmhv+VQQvOuHHjkJaWhq1bt2LTpk3YtWsXpk6det3z8/LykJeXhw8++ADHjx/H6tWrkZCQgMmTJ1917qpVq3Dx4kX9MWrUKAO+EiKyFFcGG/9yJA9FZZwyTpbl+4PZKKupR4iHA+7u5Ck6zm2xMtSFT548iYSEBBw4cAB9+vQBACxatAj3338/PvjgA/j5Xb3devfu3fHDDz/of92xY0e89dZbGD9+POrr62Fl9WdcV1dX+Pj4GCo+EVmoXoFuiAhwRWp2Kb7YdwGz7+ssOhJRm9DpZKxJugAAmDggGAqFJDjR7THYHZykpCS4urrqyw0AxMTEQKFQYP/+/c2+jlqthrOzc5NyAwDTp0+Hh4cH+vXrh5UrV0KW5eteo6amBhqNpslBRHQ9Tw9quDX/5b4LqK7TCk5D1DZ2nClERnEFnGytMLq3v+g4t81gBSc/Px9eXl5NHrOysoK7uzvy85s3BbO4uBhvvPHGVR9rvf766/j222+xdetWjB49Gs8++ywWLVp03essWLAALi4u+iMgwDTn9BNR2xh2hw/au9qhpKIWGw7nio5D1CZWNE4NH9s3AA4qg33A02ZaXHDmzp17zUG+fz1OnTp128E0Gg1GjBiBbt264bXXXmvytVdffRUDBgxAr1698PLLL+Oll17C+++/f91rxcfHQ61W64/sbK5USkTXZ6VU6HdOXrE7Azrd9e8QE5mDtDw19qRfglIhYYIJTw3/qxZXtDlz5mDixIk3PCckJAQ+Pj4oLCxs8nh9fT1KSkpuOnamrKwMw4YNg5OTEzZs2ABra+sbnh8VFYU33ngDNTU1UKlUV31dpVJd83Eiout5vG8APv79LNILy7HzbBHu6eJ18ycRmagrd2+Gd/eBv5u94DSto8UFx9PTE56eNx9ZHR0djdLSUqSkpCAyMhIAsG3bNuh0OkRFRV33eRqNBrGxsVCpVNi4cSNsbW1v+r1SU1Ph5ubGEkNErcbZ1hpj+gZgxe4MrNydwYJDZqtAU41fjuQBAJ4eFCI4Tesx2Bicrl27YtiwYZgyZQqSk5OxZ88ezJgxA2PHjtXPoMrNzUVYWBiSk5MBNJSboUOHoqKiAitWrIBGo0F+fj7y8/Oh1TYM9Pvll1/w+eef4/jx40hPT8eSJUvw9ttvY+bMmYZ6KURkoSb2D4ZCAv44W4xT+ZycQOZpzd5M1Gll9A1umEFoLgw6imjdunWYMWMGhgwZAoVCgdGjR2PhwoX6r9fV1eH06dOorKwEABw6dEg/wyo0NLTJtTIyMhAcHAxra2ssXrwYL7zwAmRZRmhoKD766CNMmTLFkC+FiCxQgLs9hnf3xa/HLmLFHxl4/7Fw0ZGIWlVlbT3W7c8CYF53bwBAkm80v9pMaTQauLi46KegExFdz6Gsy3jkP3tho1Rg99x74OV084/NiUzF2qRMzPs5DUHt7LFtzmAojXztm5a8f3MvKiKiG+gd6Ibega6o1erwZeMiaETmQKuT9YOLJw/sYPTlpqVYcIiIbuLKrfsvuPAfmZHfTxbgwqVKuNhZ49FI01/Y73+x4BAR3cTQbt7wd7PD5co6/HiIC/+Refj8j/MAgHFRgbC3Mf2F/f4XCw4R0U00LPzXsH3Dit3nufAfmbzU7FIcyLwMa6X5LOz3v1hwiIia4fE+/nBSWeFcUQV2nikSHYfotly5ezMy3A/ezuY5cJ4Fh4ioGZxsrTG2X8M+dssb3xyITFHO5Ur8drxhT8inB5rX1PC/YsEhImqmiQMaZprsPXcJx3PVouMQ3ZLVezKh1ckYENoO3fzMd6kUFhwiomZq72qHB3r6AgA+28W7OGR6yqrrsP5Aw4bT5raw3/9iwSEiaoGpdzW8Kfx6NA/ZJZWC0xC1zPrkbJTX1CPUyxF3d7r5vpKmjAWHiKgF7vBzwaBOHtDJf+7ATGQKaut1+j+zUwZ1gMLMFvb7Xyw4REQt9MzdHQEA6w9koaSiVnAaoub5OTUX+ZpqeDmpMKpXe9FxDI4Fh4iohfp3bIc7/JxRXafDF9y+gUyATidjWeO4sacGdoDKSik4keGx4BARtZAkSfh7412cNUmZ3L6BjN62U4U4W1gOJ5UV/hYVKDpOm2DBISK6Bfd394G/mx1KKmrxXUqO6DhEN/TZrnMAgL/dGQhnW2vBadoGCw4R0S2wUirw9MCG7RuW7zoPLbdvICOVcqEEBzIvw0apwFONW45YAhYcIqJb9HjfALjaWyOrpBIJjSvDEhmbpTsbxt483Ku92W7LcC0sOEREt8jexgpx0cEAgGW7zkGWeReHjEt6YRm2niiAJAFT7zbvhf3+FwsOEdFtmBAdBJWVAkdy1Nh3vkR0HKImrsycuq+rNzp6OgpO07ZYcIiIbkM7RxUe6+MP4M+BnETGIF9djQ2HcwEAzwzuKDhN22PBISK6TU8PDIFCAnacLsKpfI3oOEQAgFV7MlCnldEv2B29A91Ex2lzLDhERLcp2MMBw7r7AACW7eQmnCSeuqoO6/ZnAQCeGWxZY2+uYMEhImoFV7Zv+PkIN+Ek8dbtv4Dymnp08XbCPV28RMcRggWHiKgV9PR3xaBOHtDqZCzdybE4JE51nRar9mQCAKbeFQJJMu9NNa+HBYeIqJVMvycUAPDdwRwUaKoFpyFL9X1KDorKauDrYosHI/xExxGGBYeIqJVEdXBHnyA31Gp1WL6LY3Go7dVpdViyo+EO4t/vCoG10nLf5i33lRMRtTJJkjD93oa7OOv2Z6GkolZwIrI0P6fmIbe0Ch6ONhjbzzI21bweFhwiolY0uLMnurd3RlWdFqv2ZIiOQxZEq5Pxn+3pAIApg0Jga60UnEgsFhwiolYkSRKmD264i7N6byY01XWCE5Gl+O+xizhfXAFXe2uMuzNIdBzhWHCIiFpZ7B0+CPVyRFl1Pb5IuiA6DlkAnU7Gp9sa7t48NaADHFVWghOJx4JDRNTKFAoJzzYujb9ydwaqarWCE5G5+/1kAU4XlMFJZYUJ/YNFxzEKLDhERAbwYLgfAtztcKmiFl8nZ4mOQ2ZMlmV82jj2Jq5/EFzsrAUnMg4GLTglJSUYN24cnJ2d4erqismTJ6O8vPyGzxk8eDAkSWpyPPPMM03OycrKwogRI2Bvbw8vLy+8+OKLqK+vN+RLISJqESulQr+68bJd51FbrxOciMzVrrPFOJqjhp21Ek8N6CA6jtEwaMEZN24c0tLSsHXrVmzatAm7du3C1KlTb/q8KVOm4OLFi/rjvffe039Nq9VixIgRqK2txd69e7FmzRqsXr0a8+bNM+RLISJqsUcj/eHtrEK+pho/HsoRHYfMkCzLWJR4FgDwt6hAtHNUCU5kPAxWcE6ePImEhAR8/vnniIqKwsCBA7Fo0SKsX78eeXl5N3yuvb09fHx89Iezs7P+a1u2bMGJEyfw5ZdfIiIiAsOHD8cbb7yBxYsXo7aWa04QkfFQWSkxZVDDRodLdp5DvZZ3cah17c8owcELl2GjVGDqXZa5qeb1GKzgJCUlwdXVFX369NE/FhMTA4VCgf3799/wuevWrYOHhwe6d++O+Ph4VFb+uXFdUlISevToAW9vb/1jsbGx0Gg0SEtLu+b1ampqoNFomhxERG3hb1GBcHewwYVLldh09KLoOGRmrsyceryvP7ydbQWnMS4GKzj5+fnw8mq6g6mVlRXc3d2Rn59/3ef97W9/w5dffont27cjPj4eX3zxBcaPH9/kun8tNwD0v77edRcsWAAXFxf9ERAQcKsvi4ioRextrDB5YMO4iEXbzkKrkwUnInNxKOsydqcXw0oh4e93dRQdx+i0uODMnTv3qkHA/3ucOnXqlgNNnToVsbGx6NGjB8aNG4e1a9diw4YNOHfu1nfnjY+Ph1qt1h/Z2dm3fC0iopaKiw6Cq701zhVVYNPRG39ET9Rcixvv3jzcqz0C3O0FpzE+LV4JaM6cOZg4ceINzwkJCYGPjw8KCwubPF5fX4+SkhL4+Pg0+/tFRUUBANLT09GxY0f4+PggOTm5yTkFBQUAcN3rqlQqqFQceEVEYjjZWmPKoBC8v/k0Pkk8iwd6+kGpkETHIhN2LEeNxFOFUEjAtMG8e3MtLS44np6e8PT0vOl50dHRKC0tRUpKCiIjIwEA27Ztg06n05eW5khNTQUA+Pr66q/71ltvobCwUP8R2NatW+Hs7Ixu3bq18NUQEbWNCf2DsfyP8zhfVIFfjuRhVK/2oiORCfv372cAAKMi2iPE01FwGuNksDE4Xbt2xbBhwzBlyhQkJydjz549mDFjBsaOHQs/Pz8AQG5uLsLCwvR3ZM6dO4c33ngDKSkpyMzMxMaNGxEXF4e77roLPXv2BAAMHToU3bp1w5NPPokjR45g8+bNeOWVVzB9+nTepSEio+WostLPqFqYyLE4dOsOZ13GtlOFUCokzBzSSXQco2XQdXDWrVuHsLAwDBkyBPfffz8GDhyIZcuW6b9eV1eH06dP62dJ2djY4Pfff8fQoUMRFhaGOXPmYPTo0fjll1/0z1Eqldi0aROUSiWio6Mxfvx4xMXF4fXXXzfkSyEium0T+gfDzd4a54srsPFIrug4ZKL+/XvDujcP92qPDh4OgtMYL0mWZYv7Z4RGo4GLiwvUanWTNXaIiAztPzvS8V7CaYR4OGDLC3fBSskdc6j5Ui6UYPSSJCgVErbPGYzAdpY1uLgl79/8L4uIqA3FRf/1Lg5nVFHL/Htrw92bxyL9La7ctBQLDhFRG3JUWWFq45oli7alc3Vjarb95y/p172Zfk+o6DhGjwWHiKiNxUUHwd3BBhnFFfjxEMfiUPNcmTn1eN8ArnvTDCw4RERtzEFlhWcb1y75+PczqKnXCk5Exm7vuWLsO18CG6WCd2+aiQWHiEiA8XcGwdfFFnnqany1P0t0HDJisizjg82nAQBj+gagvaud4ESmgQWHiEgAW2slnmtcw2Tx9nRU1NQLTkTG6veThTiUVQpbawVm3su7N83FgkNEJMijkf4IbmeP4vJarN6bKToOGSGt7s+7N5MGdIAXdwxvNhYcIiJBrJUKvHBfZwDA0p3noK6sE5yIjM3GI7k4XVAGZ1srPMMdw1uEBYeISKCRPf0Q5uOEsup6fLbrnOg4ZERq63X4aGvDzKlnBneEi7214ESmhQWHiEgghULCnKFdAACr9mSisKxacCIyFusPZCG7pApeTipM6t9BdByTw4JDRCRYTFcvRAS4oqpOi0WJ6aLjkBGorK3HwsY/CzOHdIKdjVJwItPDgkNEJJgkSXh5WBgA4OvkLJwvKheciERbtScTxeU1CGpnj7F9A0THMUksOERERiC6YzvcG+aFep2M9xJOi45DAl2uqMXSnQ3jsWbf1xnW3JD1lvCnRkRkJOYOD4NCAhLS8nEws0R0HBLkk8SzKKuuR1dfZ4zs6Sc6jsliwSEiMhKdvZ3weJ+GjyPe/u9JyLIsOBG1tYziCny57wIA4JURXaFQSIITmS4WHCIiI/LCfZ1hZ63EoaxSJBzPFx2H2tg7v51EvU7GPV08MSDUQ3Qck8aCQ0RkRLydbTFlUMOU4HcTTqFOqxOciNpKckYJNqcVQCEB/7y/q+g4Jo8Fh4jIyEy9uyM8HG2QeamSG3FaCJ1Oxlu/ngAAjO0XiE7eToITmT4WHCIiI+OossLzMQ1bOHySeBaaam7hYO5+OZqHIzlqONgo8ULj7z3dHhYcIiIjNLZvADp6OqCkohaLEs+KjkMGVF2n1S8NMG1wR3g6qQQnMg8sOERERshaqcCrD3QD0LDo2zku/me2Vu3JRG5pFXycbTF5YIjoOGaDBYeIyEgN7uKlX/zvzU0nRMchAyjQVOPTbQ136F6M7cItGVoRCw4RkRF7ZURXWCslbD9dhO2nCkXHoVb2zm+nUFGrRa9AVzzcq73oOGaFBYeIyIiFeDpi0oCGaeNvbDqB2npOGzcXBzNLsOFwLiQJeG3kHVzUr5Wx4BARGbmZ94bCw9EG54srsDYpU3QcagVanYz5G9MAAI9HBiA8wFVsIDPEgkNEZOScbK3xUmzDbuOf/H4WxeU1ghPR7frmQDbS8jRwsrXCi8O6iI5jllhwiIhMwKOR/ujR3gVlNfV4L+GU6Dh0G9SVdXh/c8Pv4QsxneHhyGnhhsCCQ0RkAhQKCa89eAcA4NuDOTjA3cZN1kdbT+NyZR06ezviyegg0XHMFgsOEZGJiAxywxP9GnYb/78Nx7hPlQlKy1Pji8bdwl8beQeslXwbNhT+ZImITMjLw8Lg7mCDMwXlWLE7Q3QcagGtTkb8j8egk4ERPX3Rn7uFGxQLDhGRCXG1t9HvNP3J72eRc7lScCJqri+SMnE0Rw0nWyvMb1ylmgzHoAWnpKQE48aNg7OzM1xdXTF58mSUl19/ufHMzExIknTN47vvvtOfd62vr1+/3pAvhYjIaIzu3R5RHdxRVafFaxu5wrEpuKiuwvubG/abenlYGLycbQUnMn8GLTjjxo1DWloatm7dik2bNmHXrl2YOnXqdc8PCAjAxYsXmxz/+te/4OjoiOHDhzc5d9WqVU3OGzVqlCFfChGR0ZAkCW893B3WSgm/nyzAlrR80ZHoJl7bmIaKWi16B7rib/0CRcexCFaGuvDJkyeRkJCAAwcOoE+fPgCARYsW4f7778cHH3wAPz+/q56jVCrh4+PT5LENGzbg8ccfh6OjY5PHXV1drzqXiMhShHo5YcqgEPxnxzm8tjENA0I94KAy2F/pdBu2pOVjc1oBrBQSFjzSkysWtxGD3cFJSkqCq6urvtwAQExMDBQKBfbv39+sa6SkpCA1NRWTJ0++6mvTp0+Hh4cH+vXrh5UrV0KW5etep6amBhqNpslBRGTqZt7bCQHudshTV+Ndro1jlMpr6vUrFk+9KwRdfJwEJ7IcBis4+fn58PLyavKYlZUV3N3dkZ/fvNupK1asQNeuXdG/f/8mj7/++uv49ttvsXXrVowePRrPPvssFi1adN3rLFiwAC4uLvojICCg5S+IiMjI2Nko8c4jPQEAa5MuIOncJcGJ6H99sPk0LqqrEehuj+eGdBIdx6K0uODMnTv3ugOBrxynTt3+vySqqqrw1VdfXfPuzauvvooBAwagV69eePnll/HSSy/h/fffv+614uPjoVar9Ud2dvZt5yMiMgYDQj3wROOYjpd/OIrK2nrBieiKpHOXsHpvJgDgrYe7w9ZaKTaQhWnxB7Zz5szBxIkTb3hOSEgIfHx8UFhY2OTx+vp6lJSUNGvszPfff4/KykrExcXd9NyoqCi88cYbqKmpgUp19ZLXKpXqmo8TEZmDf94fhp2nC5FVUon3N5/G/JF3iI5k8Spq6vHi90cAAE/0C8SgTp6CE1meFhccT09PeHre/DcqOjoapaWlSElJQWRkJABg27Zt0Ol0iIqKuunzV6xYgQcffLBZ3ys1NRVubm4sMURkkZxsrbFgdE9MWJmM1XszcX8PX/QNdhcdy6K9/d+TyLlchfaudvi/EV1Fx7FIBhuD07VrVwwbNgxTpkxBcnIy9uzZgxkzZmDs2LH6GVS5ubkICwtDcnJyk+emp6dj165dePrpp6+67i+//ILPP/8cx48fR3p6OpYsWYK3334bM2fONNRLISIyend39sTjffwhy8BL3x9FVa1WdCSL9cfZIqzbnwUAeP/RnnDk7DYhDLoOzrp16xAWFoYhQ4bg/vvvx8CBA7Fs2TL91+vq6nD69GlUVjZdiXPlypXw9/fH0KFDr7qmtbU1Fi9ejOjoaEREROCzzz7DRx99hPnz5xvypRARGb3/G9EN3s4qZBRX4IMtp0XHsUia6jq8/P1RAEBcdBC3YxBIkm80v9pMaTQauLi4QK1Ww9nZWXQcIqJWs/1UISatPgAA+GJyP479aGMvfX8E3x7MQaC7PRJmDYK9De/etKaWvH9zLyoiIjNyT5gXnrwzCAAw+9sjuFReIziR5diSlo9vD+ZAkoAPHgtnuRGMBYeIyMz834iu6OTliKKyGrz8w9EbLoRKrSOvtAovNn409fTADujXgYO8RWPBISIyM7bWSix8ohdslAr8frIQX+67IDqSWavX6vD8+sNQV9Whp78LXowNEx2JwIJDRGSWuvo64+XhDW+0b/56EmcKygQnMl8Lt6XjQOZlOKqssOiJXrCx4lurMeDvAhGRmZrUPxh3d/ZETb0Oz319GNV1nDre2vadv4RPt50F0LBacVA7B8GJ6AoWHCIiM6VQSPjgsXC0c7DBqfwyzPv5OMfjtKLLFbWYtT4VOhl4NNIfD0W0Fx2J/oIFh4jIjHk6qfDJ2F5QSMC3B3Ow/gD34msNWp2M2d+mIl9TjRBPB/zrQW6PYWxYcIiIzNzATh6YM7QLAGD+z2lIzS4VG8gM/HvrGWw/XQSVlQKLnugFB65WbHRYcIiILMCzgztiaDdv1Gp1ePbLFK6Pcxv+e+wiPt2eDgB4d3RP3OHnIjgRXQsLDhGRBZAkCR88Ho4QDwfkqasx8+vDqNfqRMcyOafyNfjHdw27hD89sANG9eK4G2PFgkNEZCGcba2x9MlI2NsosffcJbybcEp0JJNSWlmLqWtTUFmrxYDQdpg7nOvdGDMWHCIiC9LZ2wnvPdoTALD8jwys289FAJujXqvDzK8PI6ukEv5udvj0id6wUvIt1Jjxd4eIyMI80NMPs2I6AQBe/ek4tp8qFJzIuMmyjFd/TsMfZ4thZ63Esif7wM3BRnQsugkWHCIiC/T8kE54NNIfOhmY/tUhHM9Vi45ktBYmpuPr5CxIEvDvMRHo5nfjXazJOLDgEBFZIEmS8PbDPTAgtB0qa7WYtPoAckurRMcyOuuTs/Dv388AAF5/qDuGdfcRnIiaiwWHiMhC2VgpsGR8JLp4O6GorAaTViVDXVknOpbR+P1EAf654RgAYMY9oXjyziDBiaglWHCIiCyYs601Vk7qCy8nFc4UlCNu5X5oqllyUi5cxoyvD0EnA49F+mPO0M6iI1ELseAQEVm49q52WDu5H9zsrXEkR40JK5NRZsEl53DWZUxclYzqOh3u6eKJtx/pAUmSRMeiFmLBISIihPk448uno+BiZ43DWaWYtOoAKmrqRcdqcykXSvDkimSUVdejX7A7Fo/rDWtOBzdJ/F0jIiIAwB1+Llj3dBScba1w8MJlTFp9AJW1llNyDmSWIG5FMspr6nFniDtWP9UX9jbcY8pUseAQEZFe9/Yu+GJyFJxUVkjOKMHEVQcsYkzOvvOXMGFlMioaVyleNbEfy42JY8EhIqImwgNcsWZyP33JGfvZPhSVme/mnNtPFWLSqgOorNViUCcPrJjQF3Y2StGx6Dax4BAR0VV6B7rh66l3wsPRBicuavDo0r04V1QuOlarW5+chafXHkRVnRZ3d/bE8rg+sLVmuTEHLDhERHRN3du74Ptn+iPA3Q4XLlXikf/sxd5zxaJjtQqtTsa7Cacw98dj0OpkPNK7PcuNmWHBISKi6wr2cMCGZwegV6Ar1FV1iFuRjLVJmZBlWXS0W6aprsOUtQexZMc5AA2L+H34WDhsrPiWaE74u0lERDfk4ajC11PuxMhwP9TrZMz7OQ2zvz1ikjOs0vLUGPXpHmw7VQiVlQIfj4nAP2K7cJ0bM8SCQ0REN2VrrcTCsRF4ZURXKBUSNhzOxchFu01mk05ZlvFFUiYe/s9enC+ugK+LLb57JhqjerUXHY0MRJJN+T7jLdJoNHBxcYFarYazM3eFJSJqiX3nL+G5rw+jsKwG1koJs2I6Y+pdIUa7IN5FdRVe/uEYdp0pAgAMCfPCB4+Fw83BRnAyaqmWvH+z4LDgEBG12OWKWsz98Sg2pxUAALr6OuPd0T3Q099VbLC/0OpkfLX/At7bfBpl1fWwsVLgpdgumDywAz+SMlEsODfBgkNEdPtkWcYPh3LxxqYTUFfVQZKAxyMDMCe2M7ycbIVmS84oweub0nA8VwOgYW2fDx8LR6iXo9BcdHtYcG6CBYeIqPUUl9fgjU0n8HNqHgDAwUaJiQOC8fTAkDb/GOh4rhofbjmN7acbPo5ysrXCi7FdMC4qCEoF79qYupa8fxvsA9O33noL/fv3h729PVxdXZv1HFmWMW/ePPj6+sLOzg4xMTE4e/Zsk3NKSkowbtw4ODs7w9XVFZMnT0Z5ufktPkVEZCo8HFX4ZGwv/DAtGuEBrqio1WLx9nMY+O42vP7LCWQUVxj0++t0MnadKcKTK/bjgUW7sf10EZQKCU/0C8S2OYMRFx3McmOBDHYHZ/78+XB1dUVOTg5WrFiB0tLSmz7n3XffxYIFC7BmzRp06NABr776Ko4dO4YTJ07A1rbhdufw4cNx8eJFfPbZZ6irq8OkSZPQt29ffPXVV83Oxjs4RESGodPJ2HqyAAsTzyItT6N/fGCoBx6M8MOw7j5wtrVule+VXliOX49exHcp2ci5XAUAUEjAAz39MCumE0I8+XGUuTGqj6hWr16NWbNm3bTgyLIMPz8/zJkzB//4xz8AAGq1Gt7e3li9ejXGjh2LkydPolu3bjhw4AD69OkDAEhISMD999+PnJwc+Pn5NSsTCw4RkWHJsoydZ4qwZm8mdpwpwpV3GmulhN6Bbrirsyd6Bbqie3uXZhUeWZaRp65GalYpDmSWYNfZIpwv+vPOkJPKCqMj/TF5YAcEuNsb6mWRYC15/zaarVIzMjKQn5+PmJgY/WMuLi6IiopCUlISxo4di6SkJLi6uurLDQDExMRAoVBg//79ePjhh6957ZqaGtTU/LlRnEajueZ5RETUOiRJwuAuXhjcxQtZlyqx8UgufkrNQ3phOfZnlGB/Ron+XG9nFQLc7OHlrIKTyhq21grU62TU1OtQUlGLwrJqZBRVoKJW2+R7WCslRHf0wKgIPwzv7ssNMqkJoyk4+fn5AABvb+8mj3t7e+u/lp+fDy8vryZft7Kygru7u/6ca1mwYAH+9a9/tXJiIiJqjsB29phxbyfMuLcTMosr8MfZIiSdv4SjOWrkXK5CgaYGBZqb71ZupZDQydsJ/YLd0K9DO9zV2QNOrfRxF5mfFhWcuXPn4t13373hOSdPnkRYWNhthWpt8fHxmD17tv7XGo0GAQEBAhMREVmmYA8HBHs44MnoYABAaWUtLlyqRFZJJUoqalFeU4/qOi2UCgnWSgXaOdjAw1GFoHb2CPZwMNrFBMn4tKjgzJkzBxMnTrzhOSEhIbcUxMfHBwBQUFAAX19f/eMFBQWIiIjQn1NYWNjkefX19SgpKdE//1pUKhVUKtUt5SIiIsNxtbeBq70NwgNcRUchM9OiguPp6QlPT0+DBOnQoQN8fHyQmJioLzQajQb79+/HtGnTAADR0dEoLS1FSkoKIiMjAQDbtm2DTqdDVFSUQXIRERGR6THYvb6srCykpqYiKysLWq0WqampSE1NbbJmTVhYGDZs2ACgYUDarFmz8Oabb2Ljxo04duwY4uLi4Ofnh1GjRgEAunbtimHDhmHKlClITk7Gnj17MGPGDIwdO7bZM6iIiIjI/BlskPG8efOwZs0a/a979eoFANi+fTsGDx4MADh9+jTU6j93on3ppZdQUVGBqVOnorS0FAMHDkRCQoJ+DRwAWLduHWbMmIEhQ4ZAoVBg9OjRWLhwoaFeBhEREZkgbtXAdXCIiIhMglFs1UBEREQkCgsOERERmR0WHCIiIjI7LDhERERkdlhwiIiIyOyw4BAREZHZYcEhIiIis8OCQ0RERGaHBYeIiIjMjsG2ajBmVxZv1mg0gpMQERFRc115327OJgwWWXDKysoAAAEBAYKTEBERUUuVlZXBxcXlhudY5F5UOp0OeXl5cHJygiRJrXptjUaDgIAAZGdnc5+r/8GfzY3x53Nj/PncGH8+18efzY2Z0s9HlmWUlZXBz88PCsWNR9lY5B0chUIBf39/g34PZ2dno/+DIgp/NjfGn8+N8edzY/z5XB9/NjdmKj+fm925uYKDjImIiMjssOAQERGR2WHBaWUqlQrz58+HSqUSHcXo8GdzY/z53Bh/PjfGn8/18WdzY+b687HIQcZERERk3ngHh4iIiMwOCw4RERGZHRYcIiIiMjssOERERGR2WHBa0eLFixEcHAxbW1tERUUhOTlZdCSjsWvXLowcORJ+fn6QJAk//fST6EhGY8GCBejbty+cnJzg5eWFUaNG4fTp06JjGY0lS5agZ8+e+kXIoqOj8dtvv4mOZZTeeecdSJKEWbNmiY5iFF577TVIktTkCAsLEx3LqOTm5mL8+PFo164d7Ozs0KNHDxw8eFB0rFbBgtNKvvnmG8yePRvz58/HoUOHEB4ejtjYWBQWFoqOZhQqKioQHh6OxYsXi45idHbu3Inp06dj37592Lp1K+rq6jB06FBUVFSIjmYU/P398c477yAlJQUHDx7Evffei4ceeghpaWmioxmVAwcO4LPPPkPPnj1FRzEqd9xxBy5evKg/du/eLTqS0bh8+TIGDBgAa2tr/Pbbbzhx4gQ+/PBDuLm5iY7WOmRqFf369ZOnT5+u/7VWq5X9/PzkBQsWCExlnADIGzZsEB3DaBUWFsoA5J07d4qOYrTc3Nzkzz//XHQMo1FWViZ36tRJ3rp1q3z33XfLzz//vOhIRmH+/PlyeHi46BhG6+WXX5YHDhwoOobB8A5OK6itrUVKSgpiYmL0jykUCsTExCApKUlgMjJFarUaAODu7i44ifHRarVYv349KioqEB0dLTqO0Zg+fTpGjBjR5O8ganD27Fn4+fkhJCQE48aNQ1ZWluhIRmPjxo3o06cPHnvsMXh5eaFXr15Yvny56FithgWnFRQXF0Or1cLb27vJ497e3sjPzxeUikyRTqfDrFmzMGDAAHTv3l10HKNx7NgxODo6QqVS4ZlnnsGGDRvQrVs30bGMwvr163Ho0CEsWLBAdBSjExUVhdWrVyMhIQFLlixBRkYGBg0ahLKyMtHRjML58+exZMkSdOrUCZs3b8a0adPw3HPPYc2aNaKjtQqL3E2cyFhNnz4dx48f5ziB/9GlSxekpqZCrVbj+++/x4QJE7Bz506LLznZ2dl4/vnnsXXrVtja2oqOY3SGDx+u//89e/ZEVFQUgoKC8O2332Ly5MkCkxkHnU6HPn364O233wYA9OrVC8ePH8fSpUsxYcIEweluH+/gtAIPDw8olUoUFBQ0ebygoAA+Pj6CUpGpmTFjBjZt2oTt27fD399fdByjYmNjg9DQUERGRmLBggUIDw/HJ598IjqWcCkpKSgsLETv3r1hZWUFKysr7Ny5EwsXLoSVlRW0Wq3oiEbF1dUVnTt3Rnp6uugoRsHX1/eqfyR07drVbD7GY8FpBTY2NoiMjERiYqL+MZ1Oh8TERI4ToJuSZRkzZszAhg0bsG3bNnTo0EF0JKOn0+lQU1MjOoZwQ4YMwbFjx5Camqo/+vTpg3HjxiE1NRVKpVJ0RKNSXl6Oc+fOwdfXV3QUozBgwICrlqQ4c+YMgoKCBCVqXfyIqpXMnj0bEyZMQJ8+fdCvXz98/PHHqKiowKRJk0RHMwrl5eVN/tWUkZGB1NRUuLu7IzAwUGAy8aZPn46vvvoKP//8M5ycnPTjtlxcXGBnZyc4nXjx8fEYPnw4AgMDUVZWhq+++go7duzA5s2bRUcTzsnJ6aqxWg4ODmjXrh3HcAH4xz/+gZEjRyIoKAh5eXmYP38+lEolnnjiCdHRjMILL7yA/v374+2338bjjz+O5ORkLFu2DMuWLRMdrXWInsZlThYtWiQHBgbKNjY2cr9+/eR9+/aJjmQ0tm/fLgO46pgwYYLoaMJd6+cCQF61apXoaEbhqaeekoOCgmQbGxvZ09NTHjJkiLxlyxbRsYwWp4n/acyYMbKvr69sY2Mjt2/fXh4zZoycnp4uOpZR+eWXX+Tu3bvLKpVKDgsLk5ctWyY6UquRZFmWBXUrIiIiIoPgGBwiIiIyOyw4REREZHZYcIiIiMjssOAQERGR2WHBISIiIrPDgkNERERmhwWHiIiIzA4LDhEREZkdFhwiIiIyOyw4REREZHZYcIiIiMjssOAQERGR2fl/dYvO+rD7BaEAAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"x = np.linspace(0, 2*np.pi, num=200)\n",
|
||
"y = np.sin(x) \n",
|
||
"\n",
|
||
"plt.plot(x, y) \n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "10d13d03-03f5-44c4-a62b-b68bf8dcaaf9",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-d81b654168ec4bc8",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Bar Charts\n",
|
||
"\n",
|
||
"Beliebt sind auch **Bar Charts** (Balkendiagramme). Bei dieser Art von Plot werden mehrere Parameter benötigt, da einfache mathematische Funktionen hier keinen direkten Sinn ergeben. \n",
|
||
"\n",
|
||
"Betrachten wir folgendes Beispiel: \n",
|
||
"\n",
|
||
"Wir wollen herausfinden, wie viele Kinder an einer Grundschule in jeder Klassenstufe sind. \n",
|
||
"\n",
|
||
"Dazu benötigen wir zwei Listen: \n",
|
||
"1. Die **Klassenstufen** \n",
|
||
"2. Die **Anzahl der Kinder** in jeder Klassenstufe \n",
|
||
"\n",
|
||
"Mit diesen Daten kann anschließend ein übersichtliches Balkendiagramm erstellt werden, das die Verteilung der Kinder über die Klassenstufen visualisiert.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 44,
|
||
"id": "06b54439-c88c-438a-9870-896280151491",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3767e976a92e292a",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"classes = [\"1. Klasse\", \"2. Klasse\", \"3. Klasse\", \"4. Klasse\"]\n",
|
||
"kids = [42, 30, 26, 45]"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "55022635-12f7-4666-991b-e802ce67c9a5",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-a702a6b994c5809e",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Plotten wir die Werte nun als Bar Chart mit der Funktion `plt.bar`:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 45,
|
||
"id": "d73faeb6-2b83-495f-b246-2e4b4c6ff784",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-8c604c68ae96c752",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAh8AAAGdCAYAAACyzRGfAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAHNdJREFUeJzt3X9019V9+PFXQkiCIQmCAiKg7IwWGcKOqCV1HeWHMoYURtyZzhVUNs52AlPZ6Spbh0ePNrQ7Q9s1Wu1xcPQUsXqGHueK89CBcgoKcfiLjeGGg44mOjsCpiUCud8/dsy3EVQSwg2Jj8c57z8+7/d9389Nric+88knpCCllAIAIJPC7l4AAPDpIj4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACCrou5ewIe1trbG/v37o7y8PAoKCrp7OQDASUgpxaFDh2LYsGFRWPjxr22ccfGxf//+GDFiRHcvAwDohH379sXw4cM/dswZFx/l5eUR8X+Lr6io6ObVAAAn4+DBgzFixIi2/49/nDMuPj74UUtFRYX4AIAe5mTeMuENpwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArIq6ewEAfDpdeNsz3b2ET623Vszq1uf3ygcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZFXU3QvI7cLbnunuJXxqvbViVncvAYAzgFc+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJDVKcXHihUroqCgIG655Za2c4cPH46ampoYNGhQ9O/fP6qrq6OxsfFU1wkA9BKdjo9t27bFAw88EOPHj293/tZbb42nn346Hn/88di0aVPs378/5s2bd8oLBQB6h07Fx3vvvRfXX399fO9734uzzz677XxTU1M89NBDsXLlypg6dWpMnDgxVq1aFT/+8Y9j69atXbZoAKDn6lR81NTUxKxZs2L69OntztfX18eRI0fanR8zZkyMHDkytmzZcsK5Wlpa4uDBg+0OAKD3KuroDWvXro2XX345tm3bdty1hoaGKC4ujgEDBrQ7P2TIkGhoaDjhfLW1tXHHHXd0dBkAQA/VoVc+9u3bFzfffHN8//vfj9LS0i5ZwLJly6Kpqant2LdvX5fMCwCcmToUH/X19fH222/HJZdcEkVFRVFUVBSbNm2Kb3/721FUVBRDhgyJ999/Pw4cONDuvsbGxhg6dOgJ5ywpKYmKiop2BwDQe3Xoxy7Tpk2L1157rd25G2+8McaMGRNf/epXY8SIEdG3b9/YsGFDVFdXR0TErl27Yu/evVFVVdV1qwYAeqwOxUd5eXmMGzeu3bmysrIYNGhQ2/mFCxfG0qVLY+DAgVFRURFLliyJqqqqmDRpUtetGgDosTr8htNPcs8990RhYWFUV1dHS0tLzJgxI+67776ufhoAoIc65fjYuHFju8elpaVRV1cXdXV1pzo1ANAL+dsuAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFl1KD7uv//+GD9+fFRUVERFRUVUVVXFD3/4w7brhw8fjpqamhg0aFD0798/qquro7GxscsXDQD0XB2Kj+HDh8eKFSuivr4+tm/fHlOnTo05c+bEG2+8ERERt956azz99NPx+OOPx6ZNm2L//v0xb96807JwAKBnKurI4NmzZ7d7fPfdd8f9998fW7dujeHDh8dDDz0Ua9asialTp0ZExKpVq+Kiiy6KrVu3xqRJk7pu1QBAj9Xp93wcO3Ys1q5dG83NzVFVVRX19fVx5MiRmD59etuYMWPGxMiRI2PLli1dslgAoOfr0CsfERGvvfZaVFVVxeHDh6N///6xbt26GDt2bOzYsSOKi4tjwIAB7cYPGTIkGhoaPnK+lpaWaGlpaXt88ODBji4JAOhBOhwfn/3sZ2PHjh3R1NQUTzzxRCxYsCA2bdrU6QXU1tbGHXfc0en74QMX3vZMdy/hU+mtFbO6ewlAD9PhH7sUFxfHr/7qr8bEiROjtrY2JkyYEN/61rdi6NCh8f7778eBAwfajW9sbIyhQ4d+5HzLli2LpqamtmPfvn0d/iAAgJ7jlP+dj9bW1mhpaYmJEydG3759Y8OGDW3Xdu3aFXv37o2qqqqPvL+kpKTtV3c/OACA3qtDP3ZZtmxZzJw5M0aOHBmHDh2KNWvWxMaNG+PZZ5+NysrKWLhwYSxdujQGDhwYFRUVsWTJkqiqqvKbLgBAmw7Fx9tvvx3z58+Pn/70p1FZWRnjx4+PZ599Nq688sqIiLjnnnuisLAwqquro6WlJWbMmBH33XffaVk4ANAzdSg+HnrooY+9XlpaGnV1dVFXV3dKiwIAei9/2wUAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyKqouxcA8HEuvO2Z7l7Cp9ZbK2Z19xLopbzyAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArDoUH7W1tXHZZZdFeXl5DB48OObOnRu7du1qN+bw4cNRU1MTgwYNiv79+0d1dXU0NjZ26aIBgJ6rQ/GxadOmqKmpia1bt8Zzzz0XR44ciauuuiqam5vbxtx6663x9NNPx+OPPx6bNm2K/fv3x7x587p84QBAz1TUkcHr169v93j16tUxePDgqK+vj9/8zd+MpqameOihh2LNmjUxderUiIhYtWpVXHTRRbF169aYNGlS160cAOiRTuk9H01NTRERMXDgwIiIqK+vjyNHjsT06dPbxowZMyZGjhwZW7ZsOeEcLS0tcfDgwXYHANB7dTo+Wltb45Zbbokrrrgixo0bFxERDQ0NUVxcHAMGDGg3dsiQIdHQ0HDCeWpra6OysrLtGDFiRGeXBAD0AJ2Oj5qamnj99ddj7dq1p7SAZcuWRVNTU9uxb9++U5oPADizdeg9Hx9YvHhx/MM//EM8//zzMXz48LbzQ4cOjffffz8OHDjQ7tWPxsbGGDp06AnnKikpiZKSks4sAwDogTr0ykdKKRYvXhzr1q2LH/3oRzFq1Kh21ydOnBh9+/aNDRs2tJ3btWtX7N27N6qqqrpmxQBAj9ahVz5qampizZo18dRTT0V5eXnb+zgqKyujX79+UVlZGQsXLoylS5fGwIEDo6KiIpYsWRJVVVV+0wUAiIgOxsf9998fERFf/OIX251ftWpV3HDDDRERcc8990RhYWFUV1dHS0tLzJgxI+67774uWSwA0PN1KD5SSp84prS0NOrq6qKurq7TiwIAei9/2wUAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgqw7Hx/PPPx+zZ8+OYcOGRUFBQTz55JPtrqeUYvny5XHeeedFv379Yvr06bF79+6uWi8A0MN1OD6am5tjwoQJUVdXd8Lr3/zmN+Pb3/52fPe7340XX3wxysrKYsaMGXH48OFTXiwA0PMVdfSGmTNnxsyZM094LaUU9957b3zta1+LOXPmRETEww8/HEOGDIknn3wyrr322lNbLQDQ43Xpez727NkTDQ0NMX369LZzlZWV8bnPfS62bNlywntaWlri4MGD7Q4AoPfq0vhoaGiIiIghQ4a0Oz9kyJC2ax9WW1sblZWVbceIESO6ckkAwBmm23/bZdmyZdHU1NR27Nu3r7uXBACcRl0aH0OHDo2IiMbGxnbnGxsb2659WElJSVRUVLQ7AIDeq0vjY9SoUTF06NDYsGFD27mDBw/Giy++GFVVVV35VABAD9Xh33Z577334s0332x7vGfPntixY0cMHDgwRo4cGbfcckvcddddMXr06Bg1alT81V/9VQwbNizmzp3blesGAHqoDsfH9u3bY8qUKW2Ply5dGhERCxYsiNWrV8ef//mfR3NzcyxatCgOHDgQv/EbvxHr16+P0tLSrls1ANBjdTg+vvjFL0ZK6SOvFxQUxJ133hl33nnnKS0MAOiduv23XQCATxfxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArE5bfNTV1cWFF14YpaWl8bnPfS5eeuml0/VUAEAPclri47HHHoulS5fG7bffHi+//HJMmDAhZsyYEW+//fbpeDoAoAc5LfGxcuXK+KM/+qO48cYbY+zYsfHd7343zjrrrPi7v/u70/F0AEAPUtTVE77//vtRX18fy5YtaztXWFgY06dPjy1bthw3vqWlJVpaWtoeNzU1RUTEwYMHu3ppERHR2vLz0zIvn+x07ekH7G33sK+9l73tvU7H3n4wZ0rpE8d2eXz8z//8Txw7diyGDBnS7vyQIUPi3/7t344bX1tbG3fcccdx50eMGNHVS6ObVd7b3SvgdLCvvZe97b1O594eOnQoKisrP3ZMl8dHRy1btiyWLl3a9ri1tTV+9rOfxaBBg6KgoKAbV3ZmOXjwYIwYMSL27dsXFRUV3b0cupC97b3sbe9kX08spRSHDh2KYcOGfeLYLo+Pc845J/r06RONjY3tzjc2NsbQoUOPG19SUhIlJSXtzg0YMKCrl9VrVFRU+I+9l7K3vZe97Z3s6/E+6RWPD3T5G06Li4tj4sSJsWHDhrZzra2tsWHDhqiqqurqpwMAepjT8mOXpUuXxoIFC+LSSy+Nyy+/PO69995obm6OG2+88XQ8HQDQg5yW+Pi93/u9eOedd2L58uXR0NAQv/7rvx7r168/7k2onLySkpK4/fbbj/sRFT2fve297G3vZF9PXUE6md+JAQDoIv62CwCQlfgAALISHwBAVuLjDPbWW29FQUFB7Nixo7uXQhfbuHFjFBQUxIEDB7p7KXQxe9s72deuJT464fnnn4/Zs2fHsGHDoqCgIJ588slOzfPhe48cORLXXXddnH/++fH66693zWLpkNra2rjsssuivLw8Bg8eHHPnzo1du3Z1aI4TReOhQ4diypQpMXbs2PjJT37SxavmZNx///0xfvz4tn8YqqqqKn74wx92aA57e2ZbsWJFFBQUxC233NKh++xrfuKjE5qbm2PChAlRV1fXZXP+/Oc/jy996Uuxbdu22Lx5c4wbN67L5ubkbdq0KWpqamLr1q3x3HPPxZEjR+Kqq66K5ubmTs/5zjvvxJQpU6K5uTleeOGFGD58eBeumJM1fPjwWLFiRdTX18f27dtj6tSpMWfOnHjjjTc6Pae9PXNs27YtHnjggRg/fvwpz2VfTz/x0QkzZ86Mu+66K37nd36nS+Y7cOBAXHnllbF///7YvHlzjBo16oTjjh07FgsXLoxRo0ZFv3794rOf/Wx861vfajdm48aNcfnll0dZWVkMGDAgrrjiiviv//qviIh45ZVXYsqUKVFeXh4VFRUxceLE2L59e9u9mzdvji984QvRr1+/GDFiRPzpn/7pKf1Ptydav3593HDDDfFrv/ZrMWHChFi9enXs3bs36uvrOzXfvn374gtf+EJUVlbGj370oxg0aNAJx7377rttr3qdddZZcfHFF8ejjz7abswTTzwRF198cfTr1y8GDRoU06dPb9ufj9v3iIinnnoqLrnkkigtLY1f+ZVfiTvuuCOOHj3aqY+pp5o9e3b89m//dowePTo+85nPxN133x39+/ePrVu3dmo+e3vmeO+99+L666+P733ve3H22Wef0lz2NQ/x0c0aGhpi8uTJEfF/33Wf6O/ffKC1tTWGDx8ejz/+eOzcuTOWL18ef/EXfxE/+MEPIiLi6NGjMXfu3Jg8eXK8+uqrsWXLlli0aFHbH+i7/vrrY/jw4bFt27aor6+P2267Lfr27RsREf/xH/8Rv/VbvxXV1dXx6quvxmOPPRabN2+OxYsXn+bPwJmtqakpIiIGDhzY4Xt37doVV1xxRYwdOzb+8R//Mfr37/+RYw8fPhwTJ06MZ555Jl5//fVYtGhRfPnLX46XXnopIiJ++tOfxnXXXRc33XRT/Ou//mts3Lgx5s2bFymlT9z3F154IebPnx8333xz7Ny5Mx544IFYvXp13H333Z34jPQOx44di7Vr10Zzc3On/uyDvT2z1NTUxKxZs2L69OmnNI99zShxSiIirVu3rtP3FhcXpzFjxqTm5ubjru/ZsydFRPqXf/mXj5yjpqYmVVdXp5RSevfdd1NEpI0bN55wbHl5eVq9evUJry1cuDAtWrSo3bkXXnghFRYWpl/84hcn+RH1LseOHUuzZs1KV1xxRYfu+2DfiouL05QpU9LRo0ePG/PP//zPKSLS//7v/37kPLNmzUp/9md/llJKqb6+PkVEeuutt44b90n7Pm3atPT1r3+93blHHnkknXfeeR34qHqHV199NZWVlaU+ffqkysrK9Mwzz3Tofnt75nn00UfTuHHj2r5OTZ48Od18880dmsO+5ic+TtGpxse8efNSYWFhWrly5XHXTxQf3/nOd9Ill1ySzjnnnFRWVpb69u2bLrvssrbrN9xwQyopKUlXX311uvfee9P+/fvbrt1+++2pqKgoTZs2LdXW1qY333yz7dqll16aiouLU1lZWdtx1llnpYhIO3fu7NTH19P98R//cbrgggvSvn37OnTfB/t2zTXXpKKiovSDH/zguDEf/kJ29OjRdOedd6Zx48als88+O5WVlaWioqL0u7/7u23Xp02blsrLy9M111yTHnzwwfSzn/2sbb6P2/dzzjknlZaWttvb0tLSFBEnjN7erKWlJe3evTtt37493Xbbbemcc85Jb7zxxknfb2/PLHv37k2DBw9Or7zyStu5U4kP+5qP+DhFpxof69atS6tXr06FhYXpb/7mb9pd/3B8PProo6m0tDTV1dWll19+Oe3evTstWrQoTZgwod19L7/8cvr617+eqqqqUv/+/dOWLVvaru3atSutXLkyXXnllam4uDj9/d//fUoppTFjxqQlS5ak3bt3H3e0tLR06uPryWpqatLw4cPTf/7nf3b43l/etzvvvDMVFRWlxx57rN2YD38hq62tTYMGDUqPPPJI2rFjR9q9e3eaNWtWmjNnTts9ra2tafPmzWn58uXp4osvTueee2679X3UvpeWlqZvfOMbJ9zbY8eOdfyT04tMmzbtuFf8Po69PbOsW7cuRUTq06dP2xERqaCgIPXp0+eEr2CciH3NT3ycoq6Ij5RSevjhh1OfPn3SX//1X7dd/3B8LF68OE2dOrXdHNOmTTsuPn7ZpEmT0pIlS0547dprr02zZ89OKaX0+7//+2natGmd+jh6k9bW1lRTU5OGDRuW/v3f/71Tc3x43+66665UVFSU1q5d2zbmw1/Irr766nTTTTe1XT927FgaPXp0uy9kv+zo0aPp/PPPPy5YP/DL+/75z3++3dz8f1OmTEkLFiw46fH29sxy8ODB9Nprr7U7Lr300vQHf/AH6bXXXjvpeexrfqflr9r2du+99168+eabbY/37NkTO3bsiIEDB8bIkSMjImLZsmXx3//93/Hwww+f1Jxf/vKXo7CwMBYsWBAppfjKV75y3JjRo0fHww8/HM8++2yMGjUqHnnkkdi2bVvbb8fs2bMnHnzwwfjSl74Uw4YNi127dsXu3btj/vz58Ytf/CK+8pWvxDXXXBOjRo2Kn/zkJ7Ft27aorq6OiIivfvWrMWnSpFi8eHH84R/+YZSVlcXOnTvjueeei+985zun+inrMWpqamLNmjXx1FNPRXl5eTQ0NERERGVlZfTr1y8iIubPnx/nn39+1NbWntScf/mXfxl9+vSJ66+/PlpbW+O66647bszo0aPjiSeeiB//+Mdx9tlnx8qVK6OxsTHGjh0bEREvvvhibNiwIa666qoYPHhwvPjii/HOO+/ERRdd9LH7HhGxfPnyuPrqq2PkyJFxzTXXRGFhYbzyyivx+uuvx1133dUVn7YeYdmyZTFz5swYOXJkHDp0KNasWRMbN26MZ599tm2Mve1ZysvLj/tnCcrKymLQoEHtztvXM1B3109P9EEBf/j45e+gFixYkCZPnvyx88QJXjVZs2ZN6tOnT1qxYsVxNX748OF0ww03pMrKyjRgwID0J3/yJ+m2225re+WjoaEhzZ07N5133nmpuLg4XXDBBWn58uXp2LFjqaWlJV177bVpxIgRqbi4OA0bNiwtXry43ZtJX3rppXTllVem/v37p7KysjR+/Ph09913d8FnrOc40b5GRFq1alXbmMmTJ3/sd8sf9Ubhb3zjG6lPnz7p+9///nHfRb377rtpzpw5qX///mnw4MHpa1/7Wpo/f37bd1E7d+5MM2bMSOeee24qKSlJn/nMZ9Lf/u3fppQ+ft8/sH79+vT5z38+9evXL1VUVKTLL788Pfjgg13xKesxbrrppnTBBRek4uLidO6556Zp06alf/qnf2o3xt72fCd6z4d9PfMUpJRS5t4BAD7F/DsfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACCr/wcQ3IzoPFeFHQAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"plt.bar(classes, kids)\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a641132d-cf1a-4e92-bdc3-55f5425b9388",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-c2444cb0f1af6626",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Bessere Datenrepräsentation\n",
|
||
"\n",
|
||
"Da die Daten aus `classes` und `kids` miteinander verknüpft sind, ist die Verwendung eines **Dictionaries** die sinnvollere Wahl, um Fehler beim Plotten zu vermeiden. \n",
|
||
"\n",
|
||
"Mit den Methoden `.keys()` und `.values()` des Dictionaries lassen sich die Daten gezielt extrahieren und anschließend plotten. \n",
|
||
"\n",
|
||
"Betrachten wir dazu folgendes Beispiel:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 46,
|
||
"id": "d21c9c59-2b84-4e87-a2f2-1388070b2419",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-1777b8fcd5bd30c4",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAh8AAAGdCAYAAACyzRGfAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAHNdJREFUeJzt3X9019V9+PFXQkiCIQmCAiKg7IwWGcKOqCV1HeWHMoYURtyZzhVUNs52AlPZ6Spbh0ePNrQ7Q9s1Wu1xcPQUsXqGHueK89CBcgoKcfiLjeGGg44mOjsCpiUCud8/dsy3EVQSwg2Jj8c57z8+7/d9389Nric+88knpCCllAIAIJPC7l4AAPDpIj4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACCrou5ewIe1trbG/v37o7y8PAoKCrp7OQDASUgpxaFDh2LYsGFRWPjxr22ccfGxf//+GDFiRHcvAwDohH379sXw4cM/dswZFx/l5eUR8X+Lr6io6ObVAAAn4+DBgzFixIi2/49/nDMuPj74UUtFRYX4AIAe5mTeMuENpwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArIq6ewEAfDpdeNsz3b2ET623Vszq1uf3ygcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZFXU3QvI7cLbnunuJXxqvbViVncvAYAzgFc+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJDVKcXHihUroqCgIG655Za2c4cPH46ampoYNGhQ9O/fP6qrq6OxsfFU1wkA9BKdjo9t27bFAw88EOPHj293/tZbb42nn346Hn/88di0aVPs378/5s2bd8oLBQB6h07Fx3vvvRfXX399fO9734uzzz677XxTU1M89NBDsXLlypg6dWpMnDgxVq1aFT/+8Y9j69atXbZoAKDn6lR81NTUxKxZs2L69OntztfX18eRI0fanR8zZkyMHDkytmzZcsK5Wlpa4uDBg+0OAKD3KuroDWvXro2XX345tm3bdty1hoaGKC4ujgEDBrQ7P2TIkGhoaDjhfLW1tXHHHXd0dBkAQA/VoVc+9u3bFzfffHN8//vfj9LS0i5ZwLJly6Kpqant2LdvX5fMCwCcmToUH/X19fH222/HJZdcEkVFRVFUVBSbNm2Kb3/721FUVBRDhgyJ999/Pw4cONDuvsbGxhg6dOgJ5ywpKYmKiop2BwDQe3Xoxy7Tpk2L1157rd25G2+8McaMGRNf/epXY8SIEdG3b9/YsGFDVFdXR0TErl27Yu/evVFVVdV1qwYAeqwOxUd5eXmMGzeu3bmysrIYNGhQ2/mFCxfG0qVLY+DAgVFRURFLliyJqqqqmDRpUtetGgDosTr8htNPcs8990RhYWFUV1dHS0tLzJgxI+67776ufhoAoIc65fjYuHFju8elpaVRV1cXdXV1pzo1ANAL+dsuAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFl1KD7uv//+GD9+fFRUVERFRUVUVVXFD3/4w7brhw8fjpqamhg0aFD0798/qquro7GxscsXDQD0XB2Kj+HDh8eKFSuivr4+tm/fHlOnTo05c+bEG2+8ERERt956azz99NPx+OOPx6ZNm2L//v0xb96807JwAKBnKurI4NmzZ7d7fPfdd8f9998fW7dujeHDh8dDDz0Ua9asialTp0ZExKpVq+Kiiy6KrVu3xqRJk7pu1QBAj9Xp93wcO3Ys1q5dG83NzVFVVRX19fVx5MiRmD59etuYMWPGxMiRI2PLli1dslgAoOfr0CsfERGvvfZaVFVVxeHDh6N///6xbt26GDt2bOzYsSOKi4tjwIAB7cYPGTIkGhoaPnK+lpaWaGlpaXt88ODBji4JAOhBOhwfn/3sZ2PHjh3R1NQUTzzxRCxYsCA2bdrU6QXU1tbGHXfc0en74QMX3vZMdy/hU+mtFbO6ewlAD9PhH7sUFxfHr/7qr8bEiROjtrY2JkyYEN/61rdi6NCh8f7778eBAwfajW9sbIyhQ4d+5HzLli2LpqamtmPfvn0d/iAAgJ7jlP+dj9bW1mhpaYmJEydG3759Y8OGDW3Xdu3aFXv37o2qqqqPvL+kpKTtV3c/OACA3qtDP3ZZtmxZzJw5M0aOHBmHDh2KNWvWxMaNG+PZZ5+NysrKWLhwYSxdujQGDhwYFRUVsWTJkqiqqvKbLgBAmw7Fx9tvvx3z58+Pn/70p1FZWRnjx4+PZ599Nq688sqIiLjnnnuisLAwqquro6WlJWbMmBH33XffaVk4ANAzdSg+HnrooY+9XlpaGnV1dVFXV3dKiwIAei9/2wUAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyKqouxcA8HEuvO2Z7l7Cp9ZbK2Z19xLopbzyAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArDoUH7W1tXHZZZdFeXl5DB48OObOnRu7du1qN+bw4cNRU1MTgwYNiv79+0d1dXU0NjZ26aIBgJ6rQ/GxadOmqKmpia1bt8Zzzz0XR44ciauuuiqam5vbxtx6663x9NNPx+OPPx6bNm2K/fv3x7x587p84QBAz1TUkcHr169v93j16tUxePDgqK+vj9/8zd+MpqameOihh2LNmjUxderUiIhYtWpVXHTRRbF169aYNGlS160cAOiRTuk9H01NTRERMXDgwIiIqK+vjyNHjsT06dPbxowZMyZGjhwZW7ZsOeEcLS0tcfDgwXYHANB7dTo+Wltb45Zbbokrrrgixo0bFxERDQ0NUVxcHAMGDGg3dsiQIdHQ0HDCeWpra6OysrLtGDFiRGeXBAD0AJ2Oj5qamnj99ddj7dq1p7SAZcuWRVNTU9uxb9++U5oPADizdeg9Hx9YvHhx/MM//EM8//zzMXz48LbzQ4cOjffffz8OHDjQ7tWPxsbGGDp06AnnKikpiZKSks4sAwDogTr0ykdKKRYvXhzr1q2LH/3oRzFq1Kh21ydOnBh9+/aNDRs2tJ3btWtX7N27N6qqqrpmxQBAj9ahVz5qampizZo18dRTT0V5eXnb+zgqKyujX79+UVlZGQsXLoylS5fGwIEDo6KiIpYsWRJVVVV+0wUAiIgOxsf9998fERFf/OIX251ftWpV3HDDDRERcc8990RhYWFUV1dHS0tLzJgxI+67774uWSwA0PN1KD5SSp84prS0NOrq6qKurq7TiwIAei9/2wUAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgqw7Hx/PPPx+zZ8+OYcOGRUFBQTz55JPtrqeUYvny5XHeeedFv379Yvr06bF79+6uWi8A0MN1OD6am5tjwoQJUVdXd8Lr3/zmN+Pb3/52fPe7340XX3wxysrKYsaMGXH48OFTXiwA0PMVdfSGmTNnxsyZM094LaUU9957b3zta1+LOXPmRETEww8/HEOGDIknn3wyrr322lNbLQDQ43Xpez727NkTDQ0NMX369LZzlZWV8bnPfS62bNlywntaWlri4MGD7Q4AoPfq0vhoaGiIiIghQ4a0Oz9kyJC2ax9WW1sblZWVbceIESO6ckkAwBmm23/bZdmyZdHU1NR27Nu3r7uXBACcRl0aH0OHDo2IiMbGxnbnGxsb2659WElJSVRUVLQ7AIDeq0vjY9SoUTF06NDYsGFD27mDBw/Giy++GFVVVV35VABAD9Xh33Z577334s0332x7vGfPntixY0cMHDgwRo4cGbfcckvcddddMXr06Bg1alT81V/9VQwbNizmzp3blesGAHqoDsfH9u3bY8qUKW2Ply5dGhERCxYsiNWrV8ef//mfR3NzcyxatCgOHDgQv/EbvxHr16+P0tLSrls1ANBjdTg+vvjFL0ZK6SOvFxQUxJ133hl33nnnKS0MAOiduv23XQCATxfxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArE5bfNTV1cWFF14YpaWl8bnPfS5eeuml0/VUAEAPclri47HHHoulS5fG7bffHi+//HJMmDAhZsyYEW+//fbpeDoAoAc5LfGxcuXK+KM/+qO48cYbY+zYsfHd7343zjrrrPi7v/u70/F0AEAPUtTVE77//vtRX18fy5YtaztXWFgY06dPjy1bthw3vqWlJVpaWtoeNzU1RUTEwYMHu3ppERHR2vLz0zIvn+x07ekH7G33sK+9l73tvU7H3n4wZ0rpE8d2eXz8z//8Txw7diyGDBnS7vyQIUPi3/7t344bX1tbG3fcccdx50eMGNHVS6ObVd7b3SvgdLCvvZe97b1O594eOnQoKisrP3ZMl8dHRy1btiyWLl3a9ri1tTV+9rOfxaBBg6KgoKAbV3ZmOXjwYIwYMSL27dsXFRUV3b0cupC97b3sbe9kX08spRSHDh2KYcOGfeLYLo+Pc845J/r06RONjY3tzjc2NsbQoUOPG19SUhIlJSXtzg0YMKCrl9VrVFRU+I+9l7K3vZe97Z3s6/E+6RWPD3T5G06Li4tj4sSJsWHDhrZzra2tsWHDhqiqqurqpwMAepjT8mOXpUuXxoIFC+LSSy+Nyy+/PO69995obm6OG2+88XQ8HQDQg5yW+Pi93/u9eOedd2L58uXR0NAQv/7rvx7r168/7k2onLySkpK4/fbbj/sRFT2fve297G3vZF9PXUE6md+JAQDoIv62CwCQlfgAALISHwBAVuLjDPbWW29FQUFB7Nixo7uXQhfbuHFjFBQUxIEDB7p7KXQxe9s72deuJT464fnnn4/Zs2fHsGHDoqCgIJ588slOzfPhe48cORLXXXddnH/++fH66693zWLpkNra2rjsssuivLw8Bg8eHHPnzo1du3Z1aI4TReOhQ4diypQpMXbs2PjJT37SxavmZNx///0xfvz4tn8YqqqqKn74wx92aA57e2ZbsWJFFBQUxC233NKh++xrfuKjE5qbm2PChAlRV1fXZXP+/Oc/jy996Uuxbdu22Lx5c4wbN67L5ubkbdq0KWpqamLr1q3x3HPPxZEjR+Kqq66K5ubmTs/5zjvvxJQpU6K5uTleeOGFGD58eBeumJM1fPjwWLFiRdTX18f27dtj6tSpMWfOnHjjjTc6Pae9PXNs27YtHnjggRg/fvwpz2VfTz/x0QkzZ86Mu+66K37nd36nS+Y7cOBAXHnllbF///7YvHlzjBo16oTjjh07FgsXLoxRo0ZFv3794rOf/Wx861vfajdm48aNcfnll0dZWVkMGDAgrrjiiviv//qviIh45ZVXYsqUKVFeXh4VFRUxceLE2L59e9u9mzdvji984QvRr1+/GDFiRPzpn/7pKf1Ptydav3593HDDDfFrv/ZrMWHChFi9enXs3bs36uvrOzXfvn374gtf+EJUVlbGj370oxg0aNAJx7377rttr3qdddZZcfHFF8ejjz7abswTTzwRF198cfTr1y8GDRoU06dPb9ufj9v3iIinnnoqLrnkkigtLY1f+ZVfiTvuuCOOHj3aqY+pp5o9e3b89m//dowePTo+85nPxN133x39+/ePrVu3dmo+e3vmeO+99+L666+P733ve3H22Wef0lz2NQ/x0c0aGhpi8uTJEfF/33Wf6O/ffKC1tTWGDx8ejz/+eOzcuTOWL18ef/EXfxE/+MEPIiLi6NGjMXfu3Jg8eXK8+uqrsWXLlli0aFHbH+i7/vrrY/jw4bFt27aor6+P2267Lfr27RsREf/xH/8Rv/VbvxXV1dXx6quvxmOPPRabN2+OxYsXn+bPwJmtqakpIiIGDhzY4Xt37doVV1xxRYwdOzb+8R//Mfr37/+RYw8fPhwTJ06MZ555Jl5//fVYtGhRfPnLX46XXnopIiJ++tOfxnXXXRc33XRT/Ou//mts3Lgx5s2bFymlT9z3F154IebPnx8333xz7Ny5Mx544IFYvXp13H333Z34jPQOx44di7Vr10Zzc3On/uyDvT2z1NTUxKxZs2L69OmnNI99zShxSiIirVu3rtP3FhcXpzFjxqTm5ubjru/ZsydFRPqXf/mXj5yjpqYmVVdXp5RSevfdd1NEpI0bN55wbHl5eVq9evUJry1cuDAtWrSo3bkXXnghFRYWpl/84hcn+RH1LseOHUuzZs1KV1xxRYfu+2DfiouL05QpU9LRo0ePG/PP//zPKSLS//7v/37kPLNmzUp/9md/llJKqb6+PkVEeuutt44b90n7Pm3atPT1r3+93blHHnkknXfeeR34qHqHV199NZWVlaU+ffqkysrK9Mwzz3Tofnt75nn00UfTuHHj2r5OTZ48Od18880dmsO+5ic+TtGpxse8efNSYWFhWrly5XHXTxQf3/nOd9Ill1ySzjnnnFRWVpb69u2bLrvssrbrN9xwQyopKUlXX311uvfee9P+/fvbrt1+++2pqKgoTZs2LdXW1qY333yz7dqll16aiouLU1lZWdtx1llnpYhIO3fu7NTH19P98R//cbrgggvSvn37OnTfB/t2zTXXpKKiovSDH/zguDEf/kJ29OjRdOedd6Zx48als88+O5WVlaWioqL0u7/7u23Xp02blsrLy9M111yTHnzwwfSzn/2sbb6P2/dzzjknlZaWttvb0tLSFBEnjN7erKWlJe3evTtt37493Xbbbemcc85Jb7zxxknfb2/PLHv37k2DBw9Or7zyStu5U4kP+5qP+DhFpxof69atS6tXr06FhYXpb/7mb9pd/3B8PProo6m0tDTV1dWll19+Oe3evTstWrQoTZgwod19L7/8cvr617+eqqqqUv/+/dOWLVvaru3atSutXLkyXXnllam4uDj9/d//fUoppTFjxqQlS5ak3bt3H3e0tLR06uPryWpqatLw4cPTf/7nf3b43l/etzvvvDMVFRWlxx57rN2YD38hq62tTYMGDUqPPPJI2rFjR9q9e3eaNWtWmjNnTts9ra2tafPmzWn58uXp4osvTueee2679X3UvpeWlqZvfOMbJ9zbY8eOdfyT04tMmzbtuFf8Po69PbOsW7cuRUTq06dP2xERqaCgIPXp0+eEr2CciH3NT3ycoq6Ij5RSevjhh1OfPn3SX//1X7dd/3B8LF68OE2dOrXdHNOmTTsuPn7ZpEmT0pIlS0547dprr02zZ89OKaX0+7//+2natGmd+jh6k9bW1lRTU5OGDRuW/v3f/71Tc3x43+66665UVFSU1q5d2zbmw1/Irr766nTTTTe1XT927FgaPXp0uy9kv+zo0aPp/PPPPy5YP/DL+/75z3++3dz8f1OmTEkLFiw46fH29sxy8ODB9Nprr7U7Lr300vQHf/AH6bXXXjvpeexrfqflr9r2du+99168+eabbY/37NkTO3bsiIEDB8bIkSMjImLZsmXx3//93/Hwww+f1Jxf/vKXo7CwMBYsWBAppfjKV75y3JjRo0fHww8/HM8++2yMGjUqHnnkkdi2bVvbb8fs2bMnHnzwwfjSl74Uw4YNi127dsXu3btj/vz58Ytf/CK+8pWvxDXXXBOjRo2Kn/zkJ7Ft27aorq6OiIivfvWrMWnSpFi8eHH84R/+YZSVlcXOnTvjueeei+985zun+inrMWpqamLNmjXx1FNPRXl5eTQ0NERERGVlZfTr1y8iIubPnx/nn39+1NbWntScf/mXfxl9+vSJ66+/PlpbW+O66647bszo0aPjiSeeiB//+Mdx9tlnx8qVK6OxsTHGjh0bEREvvvhibNiwIa666qoYPHhwvPjii/HOO+/ERRdd9LH7HhGxfPnyuPrqq2PkyJFxzTXXRGFhYbzyyivx+uuvx1133dUVn7YeYdmyZTFz5swYOXJkHDp0KNasWRMbN26MZ599tm2Mve1ZysvLj/tnCcrKymLQoEHtztvXM1B3109P9EEBf/j45e+gFixYkCZPnvyx88QJXjVZs2ZN6tOnT1qxYsVxNX748OF0ww03pMrKyjRgwID0J3/yJ+m2225re+WjoaEhzZ07N5133nmpuLg4XXDBBWn58uXp2LFjqaWlJV177bVpxIgRqbi4OA0bNiwtXry43ZtJX3rppXTllVem/v37p7KysjR+/Ph09913d8FnrOc40b5GRFq1alXbmMmTJ3/sd8sf9Ubhb3zjG6lPnz7p+9///nHfRb377rtpzpw5qX///mnw4MHpa1/7Wpo/f37bd1E7d+5MM2bMSOeee24qKSlJn/nMZ9Lf/u3fppQ+ft8/sH79+vT5z38+9evXL1VUVKTLL788Pfjgg13xKesxbrrppnTBBRek4uLidO6556Zp06alf/qnf2o3xt72fCd6z4d9PfMUpJRS5t4BAD7F/DsfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACCr/wcQ3IzoPFeFHQAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"# Definiere ein Dictionary welches die Anzahl der Schüler ihrer Klasse zuweist \n",
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.bar(school.keys(), school.values()) # Plotte mit den Werten des Dictionarys\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a921963b-94df-4c6a-81f7-c3a3fb09b7c0",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-d2c659803a58f15e",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Styling\n",
|
||
"\n",
|
||
"Auch **Bar Plots** können gestylt werden, um die Darstellung anschaulicher zu machen. \n",
|
||
"\n",
|
||
"Hierzu wird dem Parameter `color` eine Liste mit Farbwerten übergeben, sodass jeder Balken individuell eingefärbt werden kann. Dies erleichtert die Unterscheidung der Kategorien und macht den Plot visuell ansprechender."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 47,
|
||
"id": "00e9f1c6-5ccd-4ea3-bcec-b2265602917f",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-a3604899d50585d2",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAh8AAAGdCAYAAACyzRGfAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAHURJREFUeJzt3X901fV9+PFXQkjA/EIQggg4dkaLDGFH1JK6jiEoY2hhhJ3pXEFl42wnMJWdrrJ1eOjRhrZnaLuq1Z5Njp4iVs/Q47rqPHSgnKJCHP5iMtzooKOJzo4EsxL58f7+seP9NoJKQvIOSR+Pcz5/5PPjfd/JO9w8uffmpiillAIAIJPi3p4AAPCLRXwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBWJb09gQ86fvx4HDhwICorK6OoqKi3pwMAnIKUUhw6dChGjRoVxcUf/djGGRcfBw4ciDFjxvT2NACALti/f3+MHj36I8854+KjsrIyIv5v8lVVVb08GwDgVLS2tsaYMWMKP8c/yhkXH+8/1VJVVSU+AKCPOZWXTHjBKQCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgq5LengAAv6g+/k+v01NSr966Rz4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AIKuS3p5AdkVFvT2DX1wp9fYMADgDeOQDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmdVnysWbMmioqK4uabby7sO3z4cNTX18ewYcOioqIi6urqorm5+XTnCQD0E12Oj+3bt8d9990XkydP7rD/lltuiSeffDIeffTR2LJlSxw4cCAWLFhw2hMFAPqHLsXHu+++G9ddd118+9vfjrPPPruwv6WlJf72b/821q5dG5dffnlMnTo1HnjggfjhD38Yzz//fLdNGgDou7oUH/X19TF37tyYNWtWh/2NjY1x5MiRDvsnTJgQY8eOjW3btp10rPb29mhtbe2wAQD9V0lnL9iwYUO89NJLsX379hOONTU1RWlpaQwZMqTD/pqammhqajrpeA0NDbF69erOTgMA6KM69cjH/v3746abborvfOc7MWjQoG6ZwMqVK6OlpaWw7d+/v1vGBQDOTJ2Kj8bGxnjrrbfioosuipKSkigpKYktW7bEN77xjSgpKYmampp477334uDBgx2ua25ujpEjR550zLKysqiqquqwAQD9V6eedpk5c2a8+uqrHfbdcMMNMWHChPjCF74QY8aMiYEDB8amTZuirq4uIiJ2794d+/bti9ra2u6bNQDQZ3UqPiorK2PSpEkd9pWXl8ewYcMK+5csWRIrVqyIoUOHRlVVVSxfvjxqa2tj2rRp3TdrAKDP6vQLTj/OnXfeGcXFxVFXVxft7e0xe/bsuOeee7r7ZgCAPqoopZR6exI/r7W1Naqrq6OlpaVnXv9RVNT9Y3JqzqxvNaDXuT/uPd1/f9yZn9/+tgsAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVp2Kj3vvvTcmT54cVVVVUVVVFbW1tfH973+/cPzw4cNRX18fw4YNi4qKiqirq4vm5uZunzQA0Hd1Kj5Gjx4da9asicbGxtixY0dcfvnlMW/evHj99dcjIuKWW26JJ598Mh599NHYsmVLHDhwIBYsWNAjEwcA+qailFI6nQGGDh0aX/va12LhwoUxfPjwWL9+fSxcuDAiIt5444244IILYtu2bTFt2rRTGq+1tTWqq6ujpaUlqqqqTmdqJ1dU1P1jcmpO71sN6HfcH/ee7r8/7szP7y6/5uPYsWOxYcOGaGtri9ra2mhsbIwjR47ErFmzCudMmDAhxo4dG9u2bevqzQAA/UxJZy949dVXo7a2Ng4fPhwVFRWxcePGmDhxYuzcuTNKS0tjyJAhHc6vqamJpqamDx2vvb092tvbCx+3trZ2dkoAQB/S6fj45Cc/GTt37oyWlpZ47LHHYvHixbFly5YuT6ChoSFWr17d5evhfZ5R6x2eTQM6q9NPu5SWlsav/MqvxNSpU6OhoSGmTJkSX//612PkyJHx3nvvxcGDBzuc39zcHCNHjvzQ8VauXBktLS2Fbf/+/Z3+JACAvuO03+fj+PHj0d7eHlOnTo2BAwfGpk2bCsd2794d+/bti9ra2g+9vqysrPCru+9vAED/1amnXVauXBlz5syJsWPHxqFDh2L9+vWxefPmePrpp6O6ujqWLFkSK1asiKFDh0ZVVVUsX748amtrT/k3XQCA/q9T8fHWW2/FokWL4ic/+UlUV1fH5MmT4+mnn44rrrgiIiLuvPPOKC4ujrq6umhvb4/Zs2fHPffc0yMTBwD6ptN+n4/u5n0++rEe/laztL3jzLoHoW/xj7b39NH3+QAA6ArxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AIKuS3p4AwEcpWl3U21P4hZVuS709Bfopj3wAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACCrTsVHQ0NDXHLJJVFZWRkjRoyI+fPnx+7duzucc/jw4aivr49hw4ZFRUVF1NXVRXNzc7dOGgDouzoVH1u2bIn6+vp4/vnn45lnnokjR47ElVdeGW1tbYVzbrnllnjyySfj0UcfjS1btsSBAwdiwYIF3T5xAKBvKkoppa5e/Pbbb8eIESNiy5Yt8Ru/8RvR0tISw4cPj/Xr18fChQsjIuKNN96ICy64ILZt2xbTpk372DFbW1ujuro6WlpaoqqqqqtT+3BFRd0/Jqem699qp8TS9o4eXtYoWm1he0u6rYcXN6xt7+n+te3Mz+/Tes1HS0tLREQMHTo0IiIaGxvjyJEjMWvWrMI5EyZMiLFjx8a2bdtOOkZ7e3u0trZ22ACA/qvL8XH8+PG4+eab47LLLotJkyZFRERTU1OUlpbGkCFDOpxbU1MTTU1NJx2noaEhqqurC9uYMWO6OiUAoA/ocnzU19fHa6+9Fhs2bDitCaxcuTJaWloK2/79+09rPADgzFbSlYuWLVsW//AP/xDPPvtsjB49urB/5MiR8d5778XBgwc7PPrR3NwcI0eOPOlYZWVlUVZW1pVpAAB9UKce+UgpxbJly2Ljxo3xgx/8IMaNG9fh+NSpU2PgwIGxadOmwr7du3fHvn37ora2tntmDAD0aZ165KO+vj7Wr18fTzzxRFRWVhZex1FdXR2DBw+O6urqWLJkSaxYsSKGDh0aVVVVsXz58qitrT2l33QBAPq/TsXHvffeGxERv/mbv9lh/wMPPBDXX399RETceeedUVxcHHV1ddHe3h6zZ8+Oe+65p1smCwD0faf1Ph89wft89GPe56Nf8j4f/Zf3+ejP+vD7fAAAdJb4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVp2Oj2effTauvvrqGDVqVBQVFcXjjz/e4XhKKVatWhXnnntuDB48OGbNmhV79uzprvkCAH1cp+Ojra0tpkyZEnffffdJj3/1q1+Nb3zjG/Gtb30rXnjhhSgvL4/Zs2fH4cOHT3uyAEDfV9LZC+bMmRNz5sw56bGUUtx1113xxS9+MebNmxcREQ8++GDU1NTE448/Htdcc83pzRYA6PO69TUfe/fujaamppg1a1ZhX3V1dXzqU5+Kbdu2nfSa9vb2aG1t7bABAP1Xt8ZHU1NTRETU1NR02F9TU1M49kENDQ1RXV1d2MaMGdOdUwIAzjC9/tsuK1eujJaWlsK2f//+3p4SANCDujU+Ro4cGRERzc3NHfY3NzcXjn1QWVlZVFVVddgAgP6rW+Nj3LhxMXLkyNi0aVNhX2tra7zwwgtRW1vbnTcFAPRRnf5tl3fffTfefPPNwsd79+6NnTt3xtChQ2Ps2LFx8803x+233x7jx4+PcePGxV/91V/FqFGjYv78+d05bwCgj+p0fOzYsSNmzJhR+HjFihUREbF48eJYt25d/Pmf/3m0tbXF0qVL4+DBg/Hrv/7r8dRTT8WgQYO6b9YAQJ9VlFJKvT2Jn9fa2hrV1dXR0tLSM6//KCrq/jE5NT38rWZpe0dP34MUrbawvSXd1tM/Hqxt7+n+te3Mz+9e/20XAOAXi/gAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWYkPACAr8QEAZCU+AICsxAcAkJX4AACyEh8AQFbiAwDISnwAAFmJDwAgK/EBAGQlPgCArMQHAJCV+AAAshIfAEBWPRYfd999d/zSL/1SDBo0KD71qU/Fiy++2FM3BQD0IT0SH4888kisWLEibrvttnjppZdiypQpMXv27Hjrrbd64uYAgD6kR+Jj7dq18Ud/9Edxww03xMSJE+Nb3/pWnHXWWfF3f/d3PXFzAEAfUtLdA7733nvR2NgYK1euLOwrLi6OWbNmxbZt2044v729Pdrb2wsft7S0REREa2trd0+N3mZN+6UeX9bDPTw+H8r9cH/W/Wv7/vdLSuljz+32+Pjv//7vOHbsWNTU1HTYX1NTE2+88cYJ5zc0NMTq1atP2D9mzJjunhq9rbq6t2dAD7Cs/Vf1Govbf/Xc2h46dCiqP+aOodvjo7NWrlwZK1asKHx8/Pjx+OlPfxrDhg2LoqKiXpzZmaW1tTXGjBkT+/fvj6qqqt6eDt3I2vZf1rZ/sq4nl1KKQ4cOxahRoz723G6Pj3POOScGDBgQzc3NHfY3NzfHyJEjTzi/rKwsysrKOuwbMmRId0+r36iqqvLN3k9Z2/7L2vZP1vVEH/eIx/u6/QWnpaWlMXXq1Ni0aVNh3/Hjx2PTpk1RW1vb3TcHAPQxPfK0y4oVK2Lx4sVx8cUXx6WXXhp33XVXtLW1xQ033NATNwcA9CE9Eh+/93u/F2+//XasWrUqmpqa4td+7dfiqaeeOuFFqJy6srKyuO222054ioq+z9r2X9a2f7Kup68oncrvxAAAdBN/2wUAyEp8AABZiQ8AICvxcQb70Y9+FEVFRbFz587engrdbPPmzVFUVBQHDx7s7anQzaxt/2Rdu5f46IJnn302rr766hg1alQUFRXF448/3qVxPnjtkSNH4tprr43zzjsvXnvtte6ZLJ3S0NAQl1xySVRWVsaIESNi/vz5sXv37k6NcbJoPHToUMyYMSMmTpwYP/7xj7t51pyKe++9NyZPnlx4Y6ja2tr4/ve/36kxrO2Zbc2aNVFUVBQ333xzp66zrvmJjy5oa2uLKVOmxN13391tY/7v//5vfPazn43t27fH1q1bY9KkSd02Nqduy5YtUV9fH88//3w888wzceTIkbjyyiujra2ty2O+/fbbMWPGjGhra4vnnnsuRo8e3Y0z5lSNHj061qxZE42NjbFjx464/PLLY968efH66693eUxre+bYvn173HfffTF58uTTHsu69jzx0QVz5syJ22+/PX7nd36nW8Y7ePBgXHHFFXHgwIHYunVrjBs37qTnHTt2LJYsWRLjxo2LwYMHxyc/+cn4+te/3uGczZs3x6WXXhrl5eUxZMiQuOyyy+I///M/IyLi5ZdfjhkzZkRlZWVUVVXF1KlTY8eOHYVrt27dGp/5zGdi8ODBMWbMmPjTP/3T0/qh2xc99dRTcf3118ev/uqvxpQpU2LdunWxb9++aGxs7NJ4+/fvj8985jNRXV0dP/jBD2LYsGEnPe+dd94pPOp11llnxYUXXhgPP/xwh3Mee+yxuPDCC2Pw4MExbNiwmDVrVmF9PmrdIyKeeOKJuOiii2LQoEHxy7/8y7F69eo4evRolz6nvurqq6+O3/7t347x48fHJz7xibjjjjuioqIinn/++S6NZ23PHO+++25cd9118e1vfzvOPvvs0xrLuuYhPnpZU1NTTJ8+PSL+73/dJ/v7N+87fvx4jB49Oh599NHYtWtXrFq1Kv7iL/4ivvvd70ZExNGjR2P+/Pkxffr0eOWVV2Lbtm2xdOnSwh/ou+6662L06NGxffv2aGxsjFtvvTUGDhwYERH//u//Hr/1W78VdXV18corr8QjjzwSW7dujWXLlvXwV+DM1tLSEhERQ4cO7fS1u3fvjssuuywmTpwY//iP/xgVFRUfeu7hw4dj6tSp8b3vfS9ee+21WLp0aXzuc5+LF198MSIifvKTn8S1114bN954Y/zrv/5rbN68ORYsWBAppY9d9+eeey4WLVoUN910U+zatSvuu+++WLduXdxxxx1d+Ir0D8eOHYsNGzZEW1tbl/7sg7U9s9TX18fcuXNj1qxZpzWOdc0ocVoiIm3cuLHL15aWlqYJEyaktra2E47v3bs3RUT6l3/5lw8do76+PtXV1aWUUnrnnXdSRKTNmzef9NzKysq0bt26kx5bsmRJWrp0aYd9zz33XCouLk4/+9nPTvEz6l+OHTuW5s6dmy677LJOXff+upWWlqYZM2ako0ePnnDOP//zP6eISP/zP//zoePMnTs3/dmf/VlKKaXGxsYUEelHP/rRCed93LrPnDkzffnLX+6w76GHHkrnnntuJz6r/uGVV15J5eXlacCAAam6ujp973vf69T11vbM8/DDD6dJkyYV7qemT5+ebrrppk6NYV3zEx+n6XTjY8GCBam4uDitXbv2hOMni49vfvOb6aKLLkrnnHNOKi8vTwMHDkyXXHJJ4fj111+fysrK0lVXXZXuuuuudODAgcKx2267LZWUlKSZM2emhoaG9OabbxaOXXzxxam0tDSVl5cXtrPOOitFRNq1a1eXPr++7o//+I/T+eefn/bv39+p695ft4ULF6aSkpL03e9+94RzPnhHdvTo0fSlL30pTZo0KZ199tmpvLw8lZSUpN/93d8tHJ85c2aqrKxMCxcuTPfff3/66U9/Whjvo9b9nHPOSYMGDeqwtoMGDUoRcdLo7c/a29vTnj170o4dO9Ktt96azjnnnPT666+f8vXW9syyb9++NGLEiPTyyy8X9p1OfFjXfMTHaTrd+Ni4cWNat25dKi4uTn/913/d4fgH4+Phhx9OgwYNSnfffXd66aWX0p49e9LSpUvTlClTOlz30ksvpS9/+cuptrY2VVRUpG3bthWO7d69O61duzZdccUVqbS0NP393/99SimlCRMmpOXLl6c9e/acsLW3t3fp8+vL6uvr0+jRo9N//Md/dPran1+3L33pS6mkpCQ98sgjHc754B1ZQ0NDGjZsWHrooYfSzp070549e9LcuXPTvHnzCtccP348bd26Na1atSpdeOGFafjw4R3m92HrPmjQoPSVr3zlpGt77Nixzn9x+pGZM2ee8IjfR7G2Z5aNGzemiEgDBgwobBGRioqK0oABA076CMbJWNf8xMdp6o74SCmlBx98MA0YMCB97WtfKxz/YHwsW7YsXX755R3GmDlz5gnx8fOmTZuWli9fftJj11xzTbr66qtTSin9/u//fpo5c2aXPo/+5Pjx46m+vj6NGjUq/du//VuXxvjgut1+++2ppKQkbdiwoXDOB+/IrrrqqnTjjTcWjh87diyNHz++wx3Zzzt69Gg677zzTgjW9/38un/605/uMDb/34wZM9LixYtP+Xxre2ZpbW1Nr776aoft4osvTn/wB3+QXn311VMex7rm1yN/1ba/e/fdd+PNN98sfLx3797YuXNnDB06NMaOHRsREStXroz/+q//igcffPCUxvzc5z4XxcXFsXjx4kgpxec///kTzhk/fnw8+OCD8fTTT8e4cePioYceiu3btxd+O2bv3r1x//33x2c/+9kYNWpU7N69O/bs2ROLFi2Kn/3sZ/H5z38+Fi5cGOPGjYsf//jHsX379qirq4uIiC984Qsxbdq0WLZsWfzhH/5hlJeXx65du+KZZ56Jb37zm6f7Jesz6uvrY/369fHEE09EZWVlNDU1RUREdXV1DB48OCIiFi1aFOedd140NDSc0ph/+Zd/GQMGDIjrrrsujh8/Htdee+0J54wfPz4ee+yx+OEPfxhnn312rF27Npqbm2PixIkREfHCCy/Epk2b4sorr4wRI0bECy+8EG+//XZccMEFH7nuERGrVq2Kq666KsaOHRsLFy6M4uLiePnll+O1116L22+/vTu+bH3CypUrY86cOTF27Ng4dOhQrF+/PjZv3hxPP/104Rxr27dUVlae8LYE5eXlMWzYsA77resZqLfrpy96v4A/uP38/6AWL16cpk+f/pHjxEkeNVm/fn0aMGBAWrNmzQk1fvjw4XT99den6urqNGTIkPQnf/In6dZbby088tHU1JTmz5+fzj333FRaWprOP//8tGrVqnTs2LHU3t6errnmmjRmzJhUWlqaRo0alZYtW9bhxaQvvvhiuuKKK1JFRUUqLy9PkydPTnfccUc3fMX6jpOta0SkBx54oHDO9OnTP/J/yx/2QuGvfOUracCAAek73/nOCf+Leuedd9K8efNSRUVFGjFiRPriF7+YFi1aVPhf1K5du9Ls2bPT8OHDU1lZWfrEJz6R/uZv/ial9NHr/r6nnnoqffrTn06DBw9OVVVV6dJLL033339/d3zJ+owbb7wxnX/++am0tDQNHz48zZw5M/3TP/1Th3Osbd93std8WNczT1FKKWXuHQDgF5j3+QAAshIfAEBW4gMAyEp8AABZiQ8AICvxAQBkJT4AgKzEBwCQlfgAALISHwBAVuIDAMhKfAAAWf0/I8zcGv+jWy4AAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"bar_colors = [\"red\", \"blue\", \"green\", \"yellow\"] # Farben definieren\n",
|
||
"\n",
|
||
"plt.bar(school.keys(), school.values(), color=bar_colors) # Farben übergeben\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a74afec9-34fd-4cfb-bcd3-db6be64ef35f",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-964f579ce46a2882",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Y-Label\n",
|
||
"\n",
|
||
"Die Beschriftung der y-Achse erfolgt mit `plt.ylabel`. \n",
|
||
"\n",
|
||
"Hierbei wird der Achsentitel als String übergeben, z. B. `plt.ylabel(\"Anzahl Kinder\")`, um die dargestellten Werte klar und verständlich zu kennzeichnen."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 48,
|
||
"id": "e9f4c9a3-e39c-4eb8-95fd-77a3b40fa249",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-21cee3bf50f011e1",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjIAAAGdCAYAAAAIbpn/AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAJYJJREFUeJzt3X9wVPW9//HXJiEJ5sdCIkmIIZRbo0gRKgEkYsvND+UiIJFg1XIFhBbrBPwR22rubaEomNgqokWtooWBEVEYwWsVKZNKMGPQEERABOGKJRYSqFySECVA8vn+4bhf14S4J+yy+0mfj5mdkXN2D+/kI+HJ7tmzLmOMEQAAgIXCgj0AAABAZxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKwVEewBAq21tVWHDh1SXFycXC5XsMcBAAA+MMaosbFRqampCgs7+/MuXT5kDh06pD59+gR7DAAA0Ak1NTVKS0s76/4uHzJxcXGSvvpGxMfHB3kaAADgi4aGBvXp08fz9/jZdPmQ+frlpPj4eEIGAADLfNdpIZzsCwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAa0UEewAAAM6dK9gD/AszQf3deUYGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtSKCPYDVXK5gT/Cvy5hgTwAACAE8IwMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrhUzIlJaWyuVy6e677/ZsO3nypAoLC5WYmKjY2FgVFBSorq4ueEMCAICQEhIhU1VVpWeeeUaDBg3y2n7PPffotdde0+rVq1VeXq5Dhw5p4sSJQZoSAACEmqCHzIkTJzR58mQtWbJEPXv29Gyvr6/X888/r4ULFyonJ0eZmZlaunSp3nnnHW3ZsiWIEwMAgFAR9JApLCzU2LFjlZeX57W9urpap0+f9trev39/paenq7Ky8qzHa25uVkNDg9cNAAB0TRHB/M1XrVqlbdu2qaqqqs2+2tpaRUZGqkePHl7bk5OTVVtbe9ZjlpSUaN68ef4eFQAAhKCgPSNTU1Oju+66Sy+88IKio6P9dtzi4mLV19d7bjU1NX47NgAACC1BC5nq6modOXJEQ4YMUUREhCIiIlReXq4nnnhCERERSk5O1qlTp3T8+HGvx9XV1SklJeWsx42KilJ8fLzXDQAAdE1Be2kpNzdXO3fu9Np22223qX///rrvvvvUp08fdevWTWVlZSooKJAk7d27VwcPHlRWVlYwRgYAACEmaCETFxengQMHem2LiYlRYmKiZ/uMGTNUVFSkhIQExcfHa/bs2crKytKIESOCMTIAAAgxQT3Z97s89thjCgsLU0FBgZqbmzV69Gg99dRTwR4LAACECJcxxgR7iEBqaGiQ2+1WfX29/8+Xcbn8ezz4rmv/bwvAMX4eB09gfh77+vd30K8jAwAA0FmEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsFdSQefrppzVo0CDFx8crPj5eWVlZWr9+vWf/yZMnVVhYqMTERMXGxqqgoEB1dXVBnBgAAISSoIZMWlqaSktLVV1dra1btyonJ0cTJkzQhx9+KEm655579Nprr2n16tUqLy/XoUOHNHHixGCODAAAQojLGGOCPcQ3JSQk6A9/+IMmTZqkXr16aeXKlZo0aZIkac+ePbrssstUWVmpESNG+HS8hoYGud1u1dfXKz4+3r/Dulz+PR58F1r/2wIIOn4eB09gfh77+vd3yJwj09LSolWrVqmpqUlZWVmqrq7W6dOnlZeX57lP//79lZ6ersrKyiBOCgAAQkVEsAfYuXOnsrKydPLkScXGxmrt2rUaMGCAtm/frsjISPXo0cPr/snJyaqtrT3r8Zqbm9Xc3Oz5dUNDQ6BGBwAAQRb0kLn00ku1fft21dfXa82aNZo6darKy8s7fbySkhLNmzfPjxPiXxGvGgYPrxoCcCLoLy1FRkbq4osvVmZmpkpKSjR48GA9/vjjSklJ0alTp3T8+HGv+9fV1SklJeWsxysuLlZ9fb3nVlNTE+CvAAAABEvQQ+bbWltb1dzcrMzMTHXr1k1lZWWefXv37tXBgweVlZV11sdHRUV53s799Q0AAHRNjl5aOn36tLp3767t27dr4MCB5/ybFxcXa8yYMUpPT1djY6NWrlypTZs2acOGDXK73ZoxY4aKioqUkJCg+Ph4zZ49W1lZWT6/YwkAAHRtjkKmW7duSk9PV0tLi19+8yNHjmjKlCk6fPiw3G63Bg0apA0bNuiaa66RJD322GMKCwtTQUGBmpubNXr0aD311FN++b0BAID9HF9H5vnnn9crr7yiFStWKCEhIVBz+Q3XkemiAnxGKEsbPJzsi87hD23wBPc6Mo7ftbR48WLt379fqamp6tu3r2JiYrz2b9u2zfm0AAAAneA4ZPLz8wMwBgAAgHMh9xEF/sZLS10ULy11WV37JxIChz+0wWPhRxQcP35czz33nIqLi3Xs2DFJX72k9I9//KNz0wIAAHSC45eWduzYoby8PLndbn366af6+c9/roSEBL3yyis6ePCgli9fHog5AQAA2nD8jExRUZGmTZumffv2KTo62rP9uuuu0+bNm/06HAAAQEcch0xVVZVuv/32NtsvuuiiDj/MEQAAwN8ch0xUVFS7nyj98ccfq1evXn4ZCgAAwBeOQ+b666/XAw88oNOnT0uSXC6XDh48qPvuu08FBQV+HxAAAOBsHIfMo48+qhMnTigpKUlffvmlRo0apYsvvlhxcXFasGBBIGYEAABol+N3Lbndbm3cuFEVFRXasWOHTpw4oSFDhigvLy8Q8wEAAJyV45D52tVXX62rr77an7MAAAA44lPIPPHEEz4f8M477+z0MAAAAE749BEF/fr18/r10aNH9cUXX6hHjx6SvrrS7wUXXKCkpCR98sknARm0s/iIgi6KjyjosviIAnQOf2iDx4KPKDhw4IDntmDBAv3whz/URx99pGPHjunYsWP66KOPNGTIED344IN++wIAAAC+i+MPjfz+97+vNWvW6IorrvDaXl1drUmTJunAgQN+HfBc8YxMF8UzMl0Wz8igc/hDGzwWPCPzTYcPH9aZM2fabG9paVFdXZ3TwwEAAHSa45DJzc3V7bffrm3btnm2VVdX64477uAt2AAA4LxyHDJ//vOflZKSoqFDhyoqKkpRUVEaPny4kpOT9dxzzwViRgAAgHY5vo5Mr1699MYbb+jjjz/Wnj17JEn9+/fXJZdc4vfhAAAAOtLpC+JdcsklxAsAAAgqxyHT0tKiZcuWqaysTEeOHFFra6vX/r/97W9+Gw4AAKAjjkPmrrvu0rJlyzR27FgNHDhQLt6nCgAAgsRxyKxatUovv/yyrrvuukDMAwAA4DPH71qKjIzUxRdfHIhZAAAAHHH8jMy9996rxx9/XIsXL+ZlJQDWcc3j51awmLlcthn+5zhkKioq9NZbb2n9+vX6wQ9+oG7dunntf+WVV/w2HAAAQEcch0yPHj10ww03BGIWAAAARxyHzNKlSwMxBwAAgGOOT/YFAAAIFT49IzNkyBCVlZWpZ8+euuKKKzo8yfebHyYJAAAQSD6FzIQJExQVFSVJys/PD+Q8AAAAPnMZY3x6P9yZM2cUEdFx9+zevVsDBgzwy2D+0tDQILfbrfr6esXHx/v34Lz9PHh8+9+201ja4Anw0vL26yAK7NuvWdfgCcy6+vr3t8/nyEyePLnD/bt371ZOTo7vEwIAAJwjn0OmsrJSv/jFL9rd99FHHyknJ0dXXXWV3wYDAAD4Lj6//XrDhg368Y9/rISEBD300EOe7Xv27FFOTo5GjBih1atXB2RIAACA9vgcMpdddpneeOMN5ebmKiEhQb/85S+1Z88eZWdna9iwYVqzZo3Cw8MDOSsAAIAXRxfEGzZsmNatW6dx48bpxIkTWrJkiTIzM7VmzZrvPBEYAADA3xzXR05OjlauXKkbb7xR1157rdauXdvm85YAAADOB59DpmfPnm0uhPf2228rOTnZa9uxY8f8MxkAAMB38DlkFi1aFMAxAAAAnPM5ZKZOnRrIOQAAABzjQyMBAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLV8etdSUVGRzwdcuHBhp4cBAABwwqeQef/993062LcvmAcAABBIPoXMW2+9Feg5AAAAHOMcGQAAYC3HHxrZ1NSk0tJSlZWV6ciRI2ptbfXa/8knn/htOAAAgI44Dpmf/exnKi8v16233qrevXtzXgwAAAgaxyGzfv16vf766xo5cmQg5gEAAPCZ43NkevbsqYSEhEDMAgAA4IjjkHnwwQc1Z84cffHFF4GYBwAAwGc+vbR0xRVXeJ0Ls3//fiUnJ+t73/ueunXr5nXfbdu2+XdCAACAs/ApZPLz8wM8BgAAgHM+hczcuXMDPQcAAIBjXBAPAABYy/Hbr1taWvTYY4/p5Zdf1sGDB3Xq1Cmv/ceOHfPbcAAAAB1x/IzMvHnztHDhQt10002qr69XUVGRJk6cqLCwMP3ud78LwIgAAADtcxwyL7zwgpYsWaJ7771XERERuuWWW/Tcc89pzpw52rJlSyBmBAAAaJfjkKmtrdXll18uSYqNjVV9fb0kady4cXr99df9Ox0AAEAHHIdMWlqaDh8+LEn6/ve/r7/+9a+SpKqqKkVFRfl3OgAAgA44DpkbbrhBZWVlkqTZs2frt7/9rTIyMjRlyhRNnz7d7wMCAACcjeN3LZWWlnr++6abblLfvn31zjvvKCMjQ+PHj/frcAAAAB1xHDLfNmLECI0YMcIfswAAADji+KWl8PBwZWdnt7leTF1dncLDwx0dq6SkRMOGDVNcXJySkpKUn5+vvXv3et3n5MmTKiwsVGJiomJjY1VQUKC6ujqnYwMAgC7IccgYY9Tc3KyhQ4fqww8/bLPPifLychUWFmrLli3auHGjTp8+rWuvvVZNTU2e+9xzzz167bXXtHr1apWXl+vQoUOaOHGi07EBAEAX5DIO6yM8PFyfffaZSktLtXTpUq1YsUITJkxQXV2dUlNT1dLS0ulhjh49qqSkJJWXl+vHP/6x6uvr1atXL61cuVKTJk2SJO3Zs0eXXXaZKisrfXpJq6GhQW63W/X19YqPj+/0bO36xieC4zxzGM1OsbTBE+CllWseixssZm4gF5d1DZ7ArKuvf3936hmZ8PBwPf7443rkkUd00003af78+Y6fjWnP19ekSUhIkCRVV1fr9OnTysvL89ynf//+Sk9PV2VlZbvHaG5uVkNDg9cNAAB0Ted0su/MmTOVkZGhG2+8UZs3bz6nQVpbW3X33Xdr5MiRGjhwoKSvLr4XGRmpHj16eN03OTlZtbW17R6npKRE8+bNO6dZAACAHRw/I9O3b1+vk3qzs7O1ZcsW1dTUnNMghYWF2rVrl1atWnVOxykuLlZ9fb3ndq5zAQCA0OX4GZkDBw602XbxxRfr/fff7/S7iWbNmqW//OUv2rx5s9LS0jzbU1JSdOrUKR0/ftzrWZm6ujqlpKS0e6yoqCiuMAwAwL+ITr+0dOrUKR05ckStra2ebS6HZ0gaYzR79mytXbtWmzZtUr9+/bz2Z2Zmqlu3biorK1NBQYEkae/evTp48KCysrI6OzoAAOgiHIfMxx9/rBkzZuidd97x2m6MkcvlcvSupcLCQq1cuVKvvvqq4uLiPOe9uN1ude/eXW63WzNmzFBRUZESEhIUHx+v2bNnKysri4vwAQAA5yFz2223KSIiQn/5y1/Uu3dvx8/CfNPTTz8tSfr3f/93r+1Lly7VtGnTJEmPPfaYwsLCVFBQoObmZo0ePVpPPfVUp39PAADQdTi+jkxMTIyqq6vVv3//QM3kV1xHpoviOjJdFteR6bq4jkxXZdl1ZAYMGKB//vOf5zQcAACAPzgOmYcffli//vWvtWnTJn3++edcfA4AAASN43Nkvr7Kbm5urtf2zpzsCwAAcC4ch8xbb70ViDkAAAAccxwyo0aNOuu+Xbt2ndMwAAAATjg+R+bbGhsb9eyzz2r48OEaPHiwP2YCAADwSadDZvPmzZo6dap69+6tRx55RDk5OdqyZYs/ZwMAAOiQo5eWamtrtWzZMj3//PNqaGjQT37yEzU3N2vdunUaMGBAoGYEAABol8/PyIwfP16XXnqpduzYoUWLFunQoUP64x//GMjZAAAAOuTzMzLr16/XnXfeqTvuuEMZGRmBnAkAAMAnPj8jU1FRocbGRmVmZurKK6/U4sWLucIvAAAIKp9DZsSIEVqyZIkOHz6s22+/XatWrVJqaqpaW1u1ceNGNTY2BnJOAACANhy/aykmJkbTp09XRUWFdu7cqXvvvVelpaVKSkrS9ddfH4gZAQAA2nVO15G59NJL9fvf/16fffaZXnzxRX/NBAAA4JNzviCeJIWHhys/P1//8z//44/DAQAA+MQvIQMAABAMhAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsRMgAAwFqEDAAAsBYhAwAArEXIAAAAaxEyAADAWoQMAACwFiEDAACsRcgAAABrETIAAMBahAwAALAWIQMAAKxFyAAAAGsFNWQ2b96s8ePHKzU1VS6XS+vWrfPab4zRnDlz1Lt3b3Xv3l15eXnat29fcIYFAAAhJ6gh09TUpMGDB+vJJ59sd//vf/97PfHEE/rTn/6kd999VzExMRo9erROnjx5nicFAAChKCKYv/mYMWM0ZsyYdvcZY7Ro0SL95je/0YQJEyRJy5cvV3JystatW6ebb775fI4KAABCUMieI3PgwAHV1tYqLy/Ps83tduvKK69UZWXlWR/X3NyshoYGrxsAAOiaQjZkamtrJUnJycle25OTkz372lNSUiK32+259enTJ6BzAgCA4AnZkOms4uJi1dfXe241NTXBHgkAAARIyIZMSkqKJKmurs5re11dnWdfe6KiohQfH+91AwAAXVPIhky/fv2UkpKisrIyz7aGhga9++67ysrKCuJkAAAgVAT1XUsnTpzQ/v37Pb8+cOCAtm/froSEBKWnp+vuu+/W/PnzlZGRoX79+um3v/2tUlNTlZ+fH7yhAQBAyAhqyGzdulXZ2dmeXxcVFUmSpk6dqmXLlunXv/61mpqaNHPmTB0/flxXX3213nzzTUVHRwdrZAAAEEJcxhgT7CECqaGhQW63W/X19f4/X8bl8u/x4LsA/2/L0gZPoH8iueaxuMFi5gZycVnX4AnMuvr693fIniMDAADwXQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWIuQAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFjLipB58skn9b3vfU/R0dG68sor9d577wV7JAAAEAJCPmReeuklFRUVae7cudq2bZsGDx6s0aNH68iRI8EeDQAABFnIh8zChQv185//XLfddpsGDBigP/3pT7rgggv05z//OdijAQCAIIsI9gAdOXXqlKqrq1VcXOzZFhYWpry8PFVWVrb7mObmZjU3N3t+XV9fL0lqaGgI7LA4v1jPLivgS3sywMfHWfFzuKsKzLp+/f+LMabD+4V0yPzzn/9US0uLkpOTvbYnJydrz5497T6mpKRE8+bNa7O9T58+AZkRQeJ2B3sCBAhL23W5S1ncrimw69rY2Ch3Bz8YQjpkOqO4uFhFRUWeX7e2turYsWNKTEyUy+UK4mShpaGhQX369FFNTY3i4+ODPQ78iLXtmljXrou1bZ8xRo2NjUpNTe3wfiEdMhdeeKHCw8NVV1fntb2urk4pKSntPiYqKkpRUVFe23r06BGoEa0XHx/PH5wuirXtmljXrou1baujZ2K+FtIn+0ZGRiozM1NlZWWeba2trSorK1NWVlYQJwMAAKEgpJ+RkaSioiJNnTpVQ4cO1fDhw7Vo0SI1NTXptttuC/ZoAAAgyEI+ZG666SYdPXpUc+bMUW1trX74wx/qzTffbHMCMJyJiorS3Llz27wMB/uxtl0T69p1sbbnxmW+631NAAAAISqkz5EBAADoCCEDAACsRcgAAABrETL/Qj799FO5XC5t37492KPAzzZt2iSXy6Xjx48HexT4EevadbG2/kPIhIDNmzdr/PjxSk1Nlcvl0rp16zp1nG8/9vTp07rlllt00UUXadeuXf4ZFo6UlJRo2LBhiouLU1JSkvLz87V3715Hx2gvQBsbG5Wdna0BAwbos88+8/PU+C5PP/20Bg0a5LmAWVZWltavX+/oGKxr6CstLZXL5dLdd9/t6HGs7flFyISApqYmDR48WE8++aTfjvnFF1/o+uuvV1VVlSoqKjRw4EC/HRu+Ky8vV2FhobZs2aKNGzfq9OnTuvbaa9XU1NTpYx49elTZ2dlqamrS22+/rbS0ND9ODF+kpaWptLRU1dXV2rp1q3JycjRhwgR9+OGHnT4m6xpaqqqq9Mwzz2jQoEHnfCzWNrAImRAwZswYzZ8/XzfccINfjnf8+HFdc801OnTokCoqKtSvX79279fS0qIZM2aoX79+6t69uy699FI9/vjjXvfZtGmThg8frpiYGPXo0UMjR47U3//+d0nSBx98oOzsbMXFxSk+Pl6ZmZnaunWr57EVFRX60Y9+pO7du6tPnz668847z+kvcBu9+eabmjZtmn7wgx9o8ODBWrZsmQ4ePKjq6upOHa+mpkY/+tGP5Ha79be//U2JiYnt3u/zzz/3PBt3wQUX6PLLL9eLL77odZ81a9bo8ssvV/fu3ZWYmKi8vDzP+nS07pL06quvasiQIYqOjta//du/ad68eTpz5kynviYbjR8/Xtddd50yMjJ0ySWXaMGCBYqNjdWWLVs6dTzWNbScOHFCkydP1pIlS9SzZ89zOhZrG3iETBdTW1urUaNGSfrq2YCzfSaV9NXHPaSlpWn16tXavXu35syZo//6r//Syy+/LEk6c+aM8vPzNWrUKO3YsUOVlZWaOXOm58M3J0+erLS0NFVVVam6ulr333+/unXrJkn63//9X/3Hf/yHCgoKtGPHDr300kuqqKjQrFmzAvwdCG319fWSpISEBMeP3bt3r0aOHKkBAwbojTfeUGxs7Fnve/LkSWVmZur111/Xrl27NHPmTN1666167733JEmHDx/WLbfcounTp+ujjz7Spk2bNHHiRBljvnPd3377bU2ZMkV33XWXdu/erWeeeUbLli3TggULOvEdsV9LS4tWrVqlpqamTn10CusaegoLCzV27Fjl5eWd03FY2/PEIKRIMmvXru30YyMjI03//v1NU1NTm/0HDhwwksz7779/1mMUFhaagoICY4wxn3/+uZFkNm3a1O594+LizLJly9rdN2PGDDNz5kyvbW+//bYJCwszX375pY9fUdfS0tJixo4da0aOHOnocV+vW2RkpMnOzjZnzpxpc5+33nrLSDL/93//d9bjjB071tx7773GGGOqq6uNJPPpp5+2ud93rXtubq556KGHvLatWLHC9O7d28FXZb8dO3aYmJgYEx4ebtxut3n99dcdPZ51DU0vvviiGThwoOfn1KhRo8xdd93l6Bis7flFyISYcw2ZiRMnmrCwMLNw4cI2+9sLmcWLF5shQ4aYCy+80MTExJhu3bqZYcOGefZPmzbNREVFmXHjxplFixaZQ4cOefbNnTvXREREmNzcXFNSUmL279/v2Td06FATGRlpYmJiPLcLLrjASDK7d+/u1Ndnu1/84hemb9++pqamxtHjvl63SZMmmYiICPPyyy+3uc+3fyieOXPGPPDAA2bgwIGmZ8+eJiYmxkRERJgbb7zRsz83N9fExcWZSZMmmWeffdYcO3bMc7yO1v3CCy800dHRXmsbHR1tJLUb0F1Vc3Oz2bdvn9m6dau5//77zYUXXmg+/PBDnx/PuoaegwcPmqSkJPPBBx94tp1LyLC25wchE2LONWTWrl1rli1bZsLCwsyjjz7qtf/bIfPiiy+a6Oho8+STT5pt27aZffv2mZkzZ5rBgwd7PW7btm3moYceMllZWSY2NtZUVlZ69u3du9csXLjQXHPNNSYyMtK88sorxhhj+vfvb2bPnm327dvX5tbc3Nypr89mhYWFJi0tzXzyySeOH/vNdXvggQdMRESEeemll7zu8+0fiiUlJSYxMdGsWLHCbN++3ezbt8+MHTvWTJgwwfOY1tZWU1FRYebMmWMuv/xy06tXL6/5zrbu0dHR5uGHH253bVtaWpx/c7qI3NzcNs9CdoR1DT1r1641kkx4eLjnJsm4XC4THh7e7jMr7WFtzy9CJsT4I2SMMWb58uUmPDzc/OEPf/Ds/3bIzJo1y+Tk5HgdIzc3t03IfNOIESPM7Nmz29138803m/HjxxtjjPnpT39qcnNzO/V1dCWtra2msLDQpKammo8//rhTx/j2us2fP99ERESYVatWee7z7R+K48aNM9OnT/fsb2lpMRkZGV4/FL/pzJkz5qKLLmoTv1/75rpfddVVXsfGV7Kzs83UqVN9vj/rGnoaGhrMzp07vW5Dhw41//mf/2l27tzp83FY2/Mr5D/9+l/BiRMntH//fs+vDxw4oO3btyshIUHp6emSpOLiYv3jH//Q8uXLfTrmrbfeqrCwME2dOlXGGP3qV79qc5+MjAwtX75cGzZsUL9+/bRixQpVVVV53uV04MABPfvss7r++uuVmpqqvXv3at++fZoyZYq+/PJL/epXv9KkSZPUr18/ffbZZ6qqqlJBQYEk6b777tOIESM0a9Ys/exnP1NMTIx2796tjRs3avHixef6LbNGYWGhVq5cqVdffVVxcXGqra2VJLndbnXv3l2SNGXKFF100UUqKSnx6Zj//d//rfDwcE2ePFmtra265ZZb2twnIyNDa9as0TvvvKOePXtq4cKFqqur04ABAyRJ7777rsrKynTttdcqKSlJ7777ro4eParLLrusw3WXpDlz5mjcuHFKT0/XpEmTFBYWpg8++EC7du3S/Pnz/fFtC3nFxcUaM2aM0tPT1djYqJUrV2rTpk3asGGD5z6sq33i4uLaXKoiJiZGiYmJXttZ2xAT7JLC/y/zb9+++a+7qVOnmlGjRnV4HLXzbM7KlStNeHi4KS0tbfOvhJMnT5pp06YZt9ttevToYe644w5z//33e56Rqa2tNfn5+aZ3794mMjLS9O3b18yZM8e0tLSY5uZmc/PNN5s+ffqYyMhIk5qaambNmuV1Iu97771nrrnmGhMbG2tiYmLMoEGDzIIFC/zwHbNHe+sqySxdutRzn1GjRnX4L/mznaT98MMPm/DwcPPCCy+0+dfd559/biZMmGBiY2NNUlKS+c1vfmOmTJni+dfd7t27zejRo02vXr1MVFSUueSSS8wf//hHY0zH6/61N99801x11VWme/fuJj4+3gwfPtw8++yz/viWWWH69Ommb9++JjIy0vTq1cvk5uaav/71r173YV27hvbOkWFtQ4vLGGPOczsBAAD4BdeRAQAA1iJkAACAtQgZAABgLUIGAABYi5ABAADWImQAAIC1CBkAAGAtQgYAAFiLkAEAANYiZAAAgLUIGQAAYC1CBgAAWOv/AVLrMfQ/TEAjAAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"bar_colors = [\"red\", \"blue\", \"green\", \"yellow\"]\n",
|
||
"\n",
|
||
"plt.bar(school.keys(), school.values(), color=bar_colors)\n",
|
||
"\n",
|
||
"plt.ylabel(\"Anzahl Kinder\") # Beschriften der Y-Achse\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "9d90f3b3-adc9-498e-9dbe-13e0c577b886",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-32dabb34444f6190",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### X-Label\n",
|
||
"\n",
|
||
"Analog dazu die Beschriftung der X-Achse mit `plt.xlabel`."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 61,
|
||
"id": "2644cc38-238e-4cec-b951-3ff88b80011e",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3737280b071f9d91",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjIAAAGwCAYAAACzXI8XAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/SrBM8AAAACXBIWXMAAA9hAAAPYQGoP6dpAAAtLUlEQVR4nO3de1TVVf7/8dcB5BI3hRAkQZ285XgpLyVZOQJlZiaJZY2T17Lxi3axK98pzbSkpsyuTlmj3/xmlk5qWVYuRjS+XkIUrVTUwrQUtEwQSlTYvz9anV8nUDnI6ZzNPB9rnbVk789nnzdny+HFPp+LwxhjBAAAYCE/bxcAAABQXwQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrBXi7AE+rrq7W/v37FR4eLofD4e1yAABAHRhjdPToUcXHx8vP79TrLo0+yOzfv18JCQneLgMAANTDvn371LJly1P2N/ogEx4eLunnFyIiIsLL1QAAgLooKytTQkKC8/f4qTT6IPPLx0kREREEGQAALHOmw0I42BcAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgrQBvFwAAwNlzeLuA/2DGq8/OigwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1ArxdgNUcDm9X8J/LGG9XAADwAazIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaPhNksrKy5HA4dNdddznbjh07poyMDEVHRyssLEzp6ekqKSnxXpEAAMCn+ESQycvL08svv6yuXbu6tN9999167733tGjRIq1evVr79+/XkCFDvFQlAADwNV4PMuXl5Ro+fLjmzJmjZs2aOdtLS0v12muvaebMmUpOTlaPHj00d+5crV27VuvXr/dixQAAwFd4PchkZGRo4MCBSk1NdWnPz8/XiRMnXNo7duyoxMRErVu37pTjVVZWqqyszOUBAAAapwBvPvnChQu1adMm5eXl1egrLi5WYGCgmjZt6tIeGxur4uLiU445Y8YMTZ06taFLBQAAPshrKzL79u3TnXfeqTfeeEPBwcENNm5mZqZKS0udj3379jXY2AAAwLd4Lcjk5+fr4MGD6t69uwICAhQQEKDVq1frueeeU0BAgGJjY3X8+HEdOXLEZb+SkhLFxcWdctygoCBFRES4PAAAQOPktY+WUlJS9Nlnn7m0jR49Wh07dtQDDzyghIQENWnSRNnZ2UpPT5ckFRYWau/evUpKSvJGyQAAwMd4LciEh4erc+fOLm2hoaGKjo52to8dO1aTJk1SVFSUIiIiNHHiRCUlJal3797eKBkAAPgYrx7seybPPPOM/Pz8lJ6ersrKSvXv318vvfSSt8sCAAA+wmGMMd4uwpPKysoUGRmp0tLShj9exuFo2PFQd437vy0At/F+7D2eeT+u6+9vr19HBgAAoL4IMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtrwaZ2bNnq2vXroqIiFBERISSkpK0YsUKZ/+xY8eUkZGh6OhohYWFKT09XSUlJV6sGAAA+BKvBpmWLVsqKytL+fn52rhxo5KTkzV48GB98cUXkqS7775b7733nhYtWqTVq1dr//79GjJkiDdLBgAAPsRhjDHeLuLXoqKi9Pe//11Dhw5VTEyMFixYoKFDh0qSduzYoQsuuEDr1q1T79696zReWVmZIiMjVVpaqoiIiIYt1uFo2PFQd7713xaA1/F+7D2eeT+u6+9vnzlGpqqqSgsXLlRFRYWSkpKUn5+vEydOKDU11blNx44dlZiYqHXr1p1ynMrKSpWVlbk8AABA4xTg7QI+++wzJSUl6dixYwoLC9OSJUvUqVMnFRQUKDAwUE2bNnXZPjY2VsXFxaccb8aMGZo6daqHq0Zjx2Kb97DYBsAdXl+R6dChgwoKCrRhwwaNHz9eI0eO1LZt2+o9XmZmpkpLS52Pffv2NWC1AADAl3h9RSYwMFBt27aVJPXo0UN5eXl69tlnNWzYMB0/flxHjhxxWZUpKSlRXFzcKccLCgpSUFCQp8sGAAA+wOsrMr9VXV2tyspK9ejRQ02aNFF2drazr7CwUHv37lVSUpIXKwQAAL7CrRWZEydOKCQkRAUFBercufNZP3lmZqYGDBigxMREHT16VAsWLFBOTo4++ugjRUZGauzYsZo0aZKioqIUERGhiRMnKikpqc5nLAEAgMbNrSDTpEkTJSYmqqqqqkGe/ODBgxoxYoQOHDigyMhIde3aVR999JGuvPJKSdIzzzwjPz8/paenq7KyUv3799dLL73UIM8NAADs5/Z1ZF577TW98847mj9/vqKiojxVV4PhOjKNlIdPbWFqvYezllA//NB6j3evI+P2wb4vvPCCdu/erfj4eLVq1UqhoaEu/Zs2bXK/WgAAgHpwO8ikpaV5oAwAAAD3+dwtChoaHy01Uny01Gg17nckeA4/tN5j4S0Kjhw5oldffVWZmZk6fPiwpJ8/Uvr222/rVy0AAEA9uP3R0tatW5WamqrIyEjt2bNHt912m6KiovTOO+9o7969ev311z1RJwAAQA1ur8hMmjRJo0aN0q5duxQcHOxsv+aaa7RmzZoGLQ4AAOB03A4yeXl5uv3222u0n3feeae9mSMAAEBDczvIBAUFqaysrEb7zp07FRMT0yBFAQAA1IXbQea6667To48+qhMnTkiSHA6H9u7dqwceeEDp6ekNXiAAAMCpuB1knn76aZWXl6t58+b66aef1LdvX7Vt21bh4eF67LHHPFEjAABArdw+aykyMlIrV65Ubm6utm7dqvLycnXv3l2pqameqA8AAOCU3A4yv7jssst02WWXNWQtAAAAbqlTkHnuuefqPOAdd9xR72IAAADcUadbFLRp08bl60OHDunHH39U06ZNJf18pd9zzjlHzZs311dffeWRQuuLWxQ0UtyioNHiFgWoH35ovceCWxQUFRU5H4899pguvPBCbd++XYcPH9bhw4e1fft2de/eXdOmTWuwbwAAAOBM3L5p5Pnnn6/FixfroosucmnPz8/X0KFDVVRU1KAFni1WZBopVmQaLVZkUD/80HqPBSsyv3bgwAGdPHmyRntVVZVKSkrcHQ4AAKDe3A4yKSkpuv3227Vp0yZnW35+vsaPH88p2AAA4HfldpD55z//qbi4OPXs2VNBQUEKCgrSxRdfrNjYWL366queqBEAAKBWbl9HJiYmRh988IF27typHTt2SJI6duyo9u3bN3hxAAAAp1PvC+K1b9+e8AIAALzK7SBTVVWlefPmKTs7WwcPHlR1dbVL/7///e8GKw4AAOB03A4yd955p+bNm6eBAweqc+fOcnCeKgAA8BK3g8zChQv19ttv65prrvFEPQAAAHXmdpAJDAxU27ZtPVELAHicYyqryN5ipnC1QzQ8t0+/vueee/Tss8/KzQsCAwAANDi3V2Ryc3O1atUqrVixQn/84x/VpEkTl/533nmnwYoDAAA4HbeDTNOmTXX99dd7ohYAAAC3uB1k5s6d64k6AAAA3Ob2MTIAAAC+ok4rMt27d1d2draaNWumiy666LTXjvn1zSQBAAA8qU5BZvDgwQoKCpIkpaWlebIeAACAOnOYOp5HffLkSQUEnD73bNu2TZ06dWqQwhpKWVmZIiMjVVpaqoiIiIYdnKsae4+HT/9nar3H01d24Doy3uPZ68gwr97jmXmt6+/vOh8jM3z48NP2b9u2TcnJyXWvEAAA4CzVOcisW7dOf/3rX2vt2759u5KTk3XppZc2WGEAAABnUufTrz/66CNdccUVioqK0uOPP+5s37Fjh5KTk9W7d28tWrTII0UCAADUps5B5oILLtAHH3yglJQURUVF6d5779WOHTvUr18/9erVS4sXL5a/v78nawUAAHDh1gXxevXqpaVLl+raa69VeXm55syZox49emjx4sVnPBAYAACgobmdPpKTk7VgwQLdcMMNuuqqq7RkyZIa91sCAAD4PdQ5yDRr1qzGhfA++eQTxcbGurQdPny4YSoDAAA4gzoHmVmzZnmwDAAAAPfVOciMHDnSk3UAAAC4jZtGAgAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwVp3OWpo0aVKdB5w5c2a9iwEAAHBHnYLM5s2b6zTYby+YBwAA4El1CjKrVq3ydB0AAABu4xgZAABgLbdvGllRUaGsrCxlZ2fr4MGDqq6udun/6quvGqw4AACA03E7yNx6661avXq1brnlFrVo0YLjYgAAgNe4HWRWrFih999/X3369PFEPQAAAHXm9jEyzZo1U1RUlCdqAQAAcIvbQWbatGmaPHmyfvzxR0/UAwAAUGd1+mjpoosucjkWZvfu3YqNjVXr1q3VpEkTl203bdrUsBUCAACcQp2CTFpamofLAAAAcF+dgsyUKVM8XQcAAIDbuCAeAACwltunX1dVVemZZ57R22+/rb179+r48eMu/YcPH26w4gAAAE7H7RWZqVOnaubMmRo2bJhKS0s1adIkDRkyRH5+fnrkkUc8UCIAAEDt3A4yb7zxhubMmaN77rlHAQEBuvnmm/Xqq69q8uTJWr9+vSdqBAAAqJXbQaa4uFhdunSRJIWFham0tFSSdO211+r9999v2OoAAABOw+0g07JlSx04cECSdP755+vjjz+WJOXl5SkoKKhhqwMAADgNt4PM9ddfr+zsbEnSxIkT9fDDD6tdu3YaMWKExowZ0+AFAgAAnIrbZy1lZWU5/z1s2DC1atVKa9euVbt27TRo0KAGLQ4AAOB03A4yv9W7d2/17t27IWoBAABwi9sfLfn7+6tfv341rhdTUlIif39/t8aaMWOGevXqpfDwcDVv3lxpaWkqLCx02ebYsWPKyMhQdHS0wsLClJ6erpKSEnfLBgAAjZDbQcYYo8rKSvXs2VNffPFFjT53rF69WhkZGVq/fr1WrlypEydO6KqrrlJFRYVzm7vvvlvvvfeeFi1apNWrV2v//v0aMmSIu2UDAIBGyGHcTB/+/v765ptvlJWVpblz52r+/PkaPHiwSkpKFB8fr6qqqnoXc+jQITVv3lyrV6/WFVdcodLSUsXExGjBggUaOnSoJGnHjh264IILtG7dulo/0qqsrFRlZaXz67KyMiUkJKi0tFQRERH1rq1Wv7ojOH5nboZmdzG13uPhqZVjKpPrLWaKJyeXefUez8xrWVmZIiMjz/j7u14rMv7+/nr22Wf11FNPadiwYZo+fbrbqzG1+eWaNFFRUZKk/Px8nThxQqmpqc5tOnbsqMTERK1bt67WMWbMmKHIyEjnIyEh4azrAgAAvumsDvYdN26c2rVrpxtuuEFr1qw5q0Kqq6t11113qU+fPurcubOkny++FxgYqKZNm7psGxsbq+Li4lrHyczM1KRJk5xf/7IiAwAAGh+3g0yrVq1cDurt16+f1q9ff9anXmdkZOjzzz9Xbm7uWY0TFBTEhfkAAPgP4XaQKSoqqtHWtm1bbd68ud5nE02YMEHLly/XmjVr1LJlS2d7XFycjh8/riNHjrisypSUlCguLq5ezwUAABqPen+0dPz4cR08eFDV1dXONoebR0gaYzRx4kQtWbJEOTk5atOmjUt/jx491KRJE2VnZys9PV2SVFhYqL179yopKam+pQMAgEbC7SCzc+dOjR07VmvXrnVpN8bI4XC4ddZSRkaGFixYoGXLlik8PNx53EtkZKRCQkIUGRmpsWPHatKkSYqKilJERIQmTpyopKQkLsIHAADcDzKjR49WQECAli9frhYtWri9CvNrs2fPliT96U9/cmmfO3euRo0aJUl65pln5Ofnp/T0dFVWVqp///566aWX6v2cAACg8XD7OjKhoaHKz89Xx44dPVVTg6rreej1wsVGvIfryDRaXEem8eI6Mo2VZdeR6dSpk7777ruzKg4AAKAhuB1knnjiCd1///3KycnR999/r7KyMpcHAADA78XtY2R+ucpuSkqKS3t9DvYFAAA4G24HmVWrVnmiDgAAALe5HWT69u17yr7PP//8rIoBAABwh9vHyPzW0aNH9corr+jiiy9Wt27dGqImAACAOql3kFmzZo1GjhypFi1a6KmnnlJycrLWr1/fkLUBAACcllsfLRUXF2vevHl67bXXVFZWphtvvFGVlZVaunSpOnXq5KkaAQAAalXnFZlBgwapQ4cO2rp1q2bNmqX9+/fr+eef92RtAAAAp1XnFZkVK1bojjvu0Pjx49WuXTtP1gQAAFAndV6Ryc3N1dGjR9WjRw9dcskleuGFF7jCLwAA8Ko6B5nevXtrzpw5OnDggG6//XYtXLhQ8fHxqq6u1sqVK3X06FFP1gkAAFCD22cthYaGasyYMcrNzdVnn32me+65R1lZWWrevLmuu+46T9QIAABQq7O6jkyHDh305JNP6ptvvtGbb77ZUDUBAADUyVlfEE+S/P39lZaWpnfffbchhgMAAKiTBgkyAAAA3kCQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtbwaZNasWaNBgwYpPj5eDodDS5cudek3xmjy5Mlq0aKFQkJClJqaql27dnmnWAAA4HO8GmQqKirUrVs3vfjii7X2P/nkk3ruuef0j3/8Qxs2bFBoaKj69++vY8eO/c6VAgAAXxTgzScfMGCABgwYUGufMUazZs3SQw89pMGDB0uSXn/9dcXGxmrp0qW66aabfs9SAQCAD/LZY2SKiopUXFys1NRUZ1tkZKQuueQSrVu37pT7VVZWqqyszOUBAAAaJ58NMsXFxZKk2NhYl/bY2FhnX21mzJihyMhI5yMhIcGjdQIAAO/x2SBTX5mZmSotLXU+9u3b5+2SAACAh/hskImLi5MklZSUuLSXlJQ4+2oTFBSkiIgIlwcAAGicfDbItGnTRnFxccrOzna2lZWVacOGDUpKSvJiZQAAwFd49ayl8vJy7d692/l1UVGRCgoKFBUVpcTERN11112aPn262rVrpzZt2ujhhx9WfHy80tLSvFc0AADwGV4NMhs3blS/fv2cX0+aNEmSNHLkSM2bN0/333+/KioqNG7cOB05ckSXXXaZPvzwQwUHB3urZAAA4EMcxhjj7SI8qaysTJGRkSotLW3442UcjoYdD3Xn4f+2TK33ePodyTGVyfUWM8WTk8u8eo9n5rWuv7999hgZAACAMyHIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsBZBBgAAWIsgAwAArEWQAQAA1iLIAAAAaxFkAACAtQgyAADAWgQZAABgLYIMAACwFkEGAABYiyADAACsRZABAADWIsgAAABrEWQAAIC1CDIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLWsCDIvvviiWrdureDgYF1yySX69NNPvV0SAADwAT4fZN566y1NmjRJU6ZM0aZNm9StWzf1799fBw8e9HZpAADAy3w+yMycOVO33XabRo8erU6dOukf//iHzjnnHP3zn//0dmkAAMDLArxdwOkcP35c+fn5yszMdLb5+fkpNTVV69atq3WfyspKVVZWOr8uLS2VJJWVlXm2WPy+mM9Gy+NTe8zD4+OUeB9urDwzr7/8fzHGnHY7nw4y3333naqqqhQbG+vSHhsbqx07dtS6z4wZMzR16tQa7QkJCR6pEV4SGentCuAhTG3jFZnF5DZOnp3Xo0ePKvI0bww+HWTqIzMzU5MmTXJ+XV1drcOHDys6OloOh8OLlfmWsrIyJSQkaN++fYqIiPB2OWhAzG3jxLw2Xsxt7YwxOnr0qOLj40+7nU8HmXPPPVf+/v4qKSlxaS8pKVFcXFyt+wQFBSkoKMilrWnTpp4q0XoRERH84DRSzG3jxLw2XsxtTadbifmFTx/sGxgYqB49eig7O9vZVl1drezsbCUlJXmxMgAA4At8ekVGkiZNmqSRI0eqZ8+euvjiizVr1ixVVFRo9OjR3i4NAAB4mc8HmWHDhunQoUOaPHmyiouLdeGFF+rDDz+scQAw3BMUFKQpU6bU+BgO9mNuGyfmtfFibs+Ow5zpvCYAAAAf5dPHyAAAAJwOQQYAAFiLIAMAAKxFkPkPsmfPHjkcDhUUFHi7FDSwnJwcORwOHTlyxNuloAExr40Xc9twCDI+YM2aNRo0aJDi4+PlcDi0dOnSeo3z231PnDihm2++Weedd54+//zzhikWbpkxY4Z69eql8PBwNW/eXGlpaSosLHRrjNoC6NGjR9WvXz916tRJ33zzTQNXjTOZPXu2unbt6ryAWVJSklasWOHWGMyr78vKypLD4dBdd93l1n7M7e+LIOMDKioq1K1bN7344osNNuaPP/6o6667Tnl5ecrNzVXnzp0bbGzU3erVq5WRkaH169dr5cqVOnHihK666ipVVFTUe8xDhw6pX79+qqio0CeffKKWLVs2YMWoi5YtWyorK0v5+fnauHGjkpOTNXjwYH3xxRf1HpN59S15eXl6+eWX1bVr17Mei7n1LIKMDxgwYICmT5+u66+/vkHGO3LkiK688krt379fubm5atOmTa3bVVVVaezYsWrTpo1CQkLUoUMHPfvssy7b5OTk6OKLL1ZoaKiaNm2qPn366Ouvv5YkbdmyRf369VN4eLgiIiLUo0cPbdy40blvbm6uLr/8coWEhCghIUF33HHHWf0Ct9GHH36oUaNG6Y9//KO6deumefPmae/evcrPz6/XePv27dPll1+uyMhI/fvf/1Z0dHSt233//ffO1bhzzjlHXbp00ZtvvumyzeLFi9WlSxeFhIQoOjpaqampzvk53bxL0rJly9S9e3cFBwfrD3/4g6ZOnaqTJ0/W63uy0aBBg3TNNdeoXbt2at++vR577DGFhYVp/fr19RqPefUt5eXlGj58uObMmaNmzZqd1VjMrecRZBqZ4uJi9e3bV9LPqwGnuieV9PPtHlq2bKlFixZp27Ztmjx5sv77v/9bb7/9tiTp5MmTSktLU9++fbV161atW7dO48aNc958c/jw4WrZsqXy8vKUn5+vBx98UE2aNJEkffnll7r66quVnp6urVu36q233lJubq4mTJjg4VfAt5WWlkqSoqKi3N63sLBQffr0UadOnfTBBx8oLCzslNseO3ZMPXr00Pvvv6/PP/9c48aN0y233KJPP/1UknTgwAHdfPPNGjNmjLZv366cnBwNGTJExpgzzvsnn3yiESNG6M4779S2bdv08ssva968eXrsscfq8YrYr6qqSgsXLlRFRUW9bp3CvPqejIwMDRw4UKmpqWc1DnP7OzHwKZLMkiVL6r1vYGCg6dixo6moqKjRX1RUZCSZzZs3n3KMjIwMk56ebowx5vvvvzeSTE5OTq3bhoeHm3nz5tXaN3bsWDNu3DiXtk8++cT4+fmZn376qY7fUeNSVVVlBg4caPr06ePWfr/MW2BgoOnXr585efJkjW1WrVplJJkffvjhlOMMHDjQ3HPPPcYYY/Lz840ks2fPnhrbnWneU1JSzOOPP+7SNn/+fNOiRQs3viv7bd261YSGhhp/f38TGRlp3n//fbf2Z15905tvvmk6d+7sfJ/q27evufPOO90ag7n9fRFkfMzZBpkhQ4YYPz8/M3PmzBr9tQWZF154wXTv3t2ce+65JjQ01DRp0sT06tXL2T9q1CgTFBRkrr32WjNr1iyzf/9+Z9+UKVNMQECASUlJMTNmzDC7d+929vXs2dMEBgaa0NBQ5+Occ84xksy2bdvq9f3Z7q9//atp1aqV2bdvn1v7/TJvQ4cONQEBAebtt9+usc1v3xRPnjxpHn30UdO5c2fTrFkzExoaagICAswNN9zg7E9JSTHh4eFm6NCh5pVXXjGHDx92jne6eT/33HNNcHCwy9wGBwcbSbUG6MaqsrLS7Nq1y2zcuNE8+OCD5txzzzVffPFFnfdnXn3P3r17TfPmzc2WLVucbWcTZJjb3wdBxsecbZBZsmSJmTdvnvHz8zNPP/20S/9vg8ybb75pgoODzYsvvmg2bdpkdu3aZcaNG2e6devmst+mTZvM448/bpKSkkxYWJhZt26ds6+wsNDMnDnTXHnllSYwMNC88847xhhjOnbsaCZOnGh27dpV41FZWVmv789mGRkZpmXLluarr75ye99fz9ujjz5qAgICzFtvveWyzW/fFGfMmGGio6PN/PnzTUFBgdm1a5cZOHCgGTx4sHOf6upqk5ubayZPnmy6dOliYmJiXOo71bwHBwebJ554ota5raqqcv/FaSRSUlJqrEKeDvPqe5YsWWIkGX9/f+dDknE4HMbf37/WlZXaMLe/L4KMj2mIIGOMMa+//rrx9/c3f//73539vw0yEyZMMMnJyS5jpKSk1Agyv9a7d28zceLEWvtuuukmM2jQIGOMMX/+859NSkpKvb6PxqS6utpkZGSY+Ph4s3PnznqN8dt5mz59ugkICDALFy50bvPbN8Vrr73WjBkzxtlfVVVl2rVr5/Km+GsnT5405513Xo3w+4tfz/ull17qMjZ+1q9fPzNy5Mg6b8+8+p6ysjLz2WefuTx69uxp/vKXv5jPPvuszuMwt78vn7/79X+C8vJy7d692/l1UVGRCgoKFBUVpcTERElSZmamvv32W73++ut1GvOWW26Rn5+fRo4cKWOM7rvvvhrbtGvXTq+//ro++ugjtWnTRvPnz1deXp7zLKeioiK98soruu666xQfH6/CwkLt2rVLI0aM0E8//aT77rtPQ4cOVZs2bfTNN98oLy9P6enpkqQHHnhAvXv31oQJE3TrrbcqNDRU27Zt08qVK/XCCy+c7UtmjYyMDC1YsEDLli1TeHi4iouLJUmRkZEKCQmRJI0YMULnnXeeZsyYUacx//a3v8nf31/Dhw9XdXW1br755hrbtGvXTosXL9batWvVrFkzzZw5UyUlJerUqZMkacOGDcrOztZVV12l5s2ba8OGDTp06JAuuOCC0867JE2ePFnXXnutEhMTNXToUPn5+WnLli36/PPPNX369IZ42XxeZmamBgwYoMTERB09elQLFixQTk6OPvroI+c2zKt9wsPDa1yqIjQ0VNHR0S7tzK2P8XaSwv9P5r99/Pqvu5EjR5q+ffuedhzVspqzYMEC4+/vb7Kysmr8lXDs2DEzatQoExkZaZo2bWrGjx9vHnzwQeeKTHFxsUlLSzMtWrQwgYGBplWrVmby5MmmqqrKVFZWmptuuskkJCSYwMBAEx8fbyZMmOByIO+nn35qrrzyShMWFmZCQ0NN165dzWOPPdYAr5g9aptXSWbu3LnObfr27Xvav+RPdZD2E088Yfz9/c0bb7xR46+777//3gwePNiEhYWZ5s2bm4ceesiMGDHC+dfdtm3bTP/+/U1MTIwJCgoy7du3N88//7wx5vTz/osPP/zQXHrppSYkJMRERESYiy++2LzyyisN8ZJZYcyYMaZVq1YmMDDQxMTEmJSUFPPxxx+7bMO8Ng61HSPD3PoWhzHG/M7ZCQAAoEFwHRkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQBn9Kc//Ul33XWXt8vwuqVLl6pt27by9/fn9QB8BEEGgEaNGqW0tDSXtsWLFys4OFhPP/20d4rykNq+17q6/fbbNXToUO3bt0/Tpk1r2MIA1AtBBkANr776qoYPH67Zs2frnnvu8XY5PqG8vFwHDx5U//79FR8fr/DwcG+XBEAEGQC/8eSTT2rixIlauHChRo8eXes28+fPV8+ePRUeHq64uDj9+c9/1sGDB539P/zwg4YPH66YmBiFhISoXbt2mjt3riTp+PHjmjBhglq0aKHg4GC1atXK5S7CR44c0a233qqYmBhFREQoOTlZW7ZscfY/8sgjuvDCCzV//ny1bt1akZGRuummm3T06FHnNosXL1aXLl0UEhKi6OhopaamqqKiQo888oj+53/+R8uWLZPD4ZDD4VBOTo5ycnLkcDh05MgR5xgFBQVyOBzas2ePcnJynMElOTnZuZ8k5ebm6vLLL1dISIgSEhJ0xx13qKKiwjlO69at9fjjj2vMmDEKDw9XYmKiXnnllfpPEAAXBBkATg888ICmTZum5cuX6/rrrz/ldidOnNC0adO0ZcsWLV26VHv27NGoUaOc/Q8//LC2bdumFStWaPv27Zo9e7bOPfdcSdJzzz2nd999V2+//bYKCwv1xhtvqHXr1s59b7jhBh08eFArVqxQfn6+unfvrpSUFB0+fNi5zZdffqmlS5dq+fLlWr58uVavXq2srCxJ0oEDB3TzzTdrzJgx2r59u3JycjRkyBAZY3Tvvffqxhtv1NVXX60DBw7owIEDuvTSS8/4ulx66aUqLCyUJP3rX/9y7vfll1/q6quvVnp6urZu3aq33npLubm5mjBhgsv+Tz/9tHr27KnNmzfrv/7rvzR+/HjneADOkpfvvg3AB4wcOdIEBgYaSSY7O7tGf9++fc2dd955yv3z8vKMJHP06FFjjDGDBg0yo0ePrnXbiRMnmuTkZFNdXV2j75NPPjERERHm2LFjLu3nn3++efnll40xxkyZMsWcc845pqyszNl/3333mUsuucQYY0x+fr6RZPbs2XPK73Xw4MEubatWrTKSzA8//OBs27x5s5FkioqKjDHG/PDDD0aSWbVqlXObsWPHmnHjxtX4Hvz8/MxPP/1kjDGmVatW5i9/+Yuzv7q62jRv3tzMnj271voAuIcVGQCSpK5du6p169aaMmWKysvLT7ttfn6+Bg0apMTERIWHh6tv376SpL1790qSxo8fr4ULF+rCCy/U/fffr7Vr1zr3HTVqlAoKCtShQwfdcccd+vjjj519W7ZsUXl5uaKjoxUWFuZ8FBUV6csvv3Ru17p1a5djVFq0aOH8aKtbt25KSUlRly5ddMMNN2jOnDn64Ycfzv4FqsWWLVs0b948l1r79++v6upqFRUVObfr2rWr898Oh0NxcXEuH8UBqD+CDABJ0nnnnaecnBx9++23uvrqq12OOfm1iooK9e/fXxEREXrjjTeUl5enJUuWSPr5+BdJGjBggL7++mvdfffd2r9/v1JSUnTvvfdKkrp3766ioiJNmzZNP/30k2688UYNHTpU0s8H1LZo0UIFBQUuj8LCQt13333OGpo0aeJSk8PhUHV1tSTJ399fK1eu1IoVK9SpUyc9//zz6tChg0uw+C0/v5/fCo0xzrYTJ06c8TUrLy/X7bff7lLrli1btGvXLp1//vl1qhfA2SHIAHBq1aqVVq9ereLi4lOGmR07duj7779XVlaWLr/8cnXs2LHW1YWYmBiNHDlS//u//6tZs2a5HOAaERGhYcOGac6cOXrrrbf0r3/9S4cPH1b37t1VXFysgIAAtW3b1uXxyzE2deFwONSnTx9NnTpVmzdvVmBgoDNsBQYGqqqqqkat0s/H1/yioKDgjM/TvXt3bdu2rUatbdu2VWBgYJ3rBVB/BBkALhISEpSTk+M81bisrMylPzExUYGBgXr++ef11Vdf6d13361xTZXJkydr2bJl2r17t7744gstX75cF1xwgSRp5syZevPNN7Vjxw7t3LlTixYtUlxcnJo2barU1FQlJSUpLS1NH3/8sfbs2aO1a9fqb3/7mzZu3Fin+jds2KDHH39cGzdu1N69e/XOO+/o0KFDzudv3bq1tm7dqsLCQn333Xc6ceKE2rZtq4SEBD3yyCPatWuX3n///TpdP+eBBx7Q2rVrNWHCBBUUFGjXrl1atmxZjYN9AXgOQQZADS1btlROTo6+++67GmEmJiZG8+bN06JFi9SpUydlZWXpqaeectk/MDBQmZmZ6tq1q6644gr5+/tr4cKFkqTw8HA9+eST6tmzp3r16qU9e/bogw8+kJ+fnxwOhz744ANdccUVGj16tNq3b6+bbrpJX3/9tWJjY+tUe0REhNasWaNrrrlG7du310MPPaSnn35aAwYMkCTddttt6tChg3r27KmYmBj93//9n5o0aeIMV127dtUTTzyh6dOnn/G5unbtqtWrV2vnzp26/PLLddFFF2ny5MmKj4+v60sN4Cw5zK8/FAYAALAIKzIAAMBaBBkAAGAtggwAALAWQQYAAFiLIAMAAKxFkAEAANYiyAAAAGsRZAAAgLUIMgAAwFoEGQAAYC2CDAAAsNb/A12LExXeD7tPAAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"bar_colors = [\"red\", \"blue\", \"green\", \"yellow\"]\n",
|
||
"\n",
|
||
"plt.bar(school.keys(), school.values(), color=bar_colors)\n",
|
||
"\n",
|
||
"plt.ylabel(\"Anzahl Kinder\") # Beschriften der Y-Achse\n",
|
||
"plt.xlabel(\"Klassenstufen\") # Beschriften der X-Achse\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "16e05c9d-80ef-47b8-a17f-df7a96398ab5",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-230328a26793cddb",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"### Aufgabe\n",
|
||
"\n",
|
||
"*5 Punkte*\n",
|
||
"\n",
|
||
"Dir liegt ein Datenset `sec_school` einer Hauptschule vor, das die Klassenstufen von 5 bis 9 auf die Anzahl ihrer Schüler im jeweiligen Jahrgang abbildet. \n",
|
||
"\n",
|
||
"Erstelle einen **Barplot** und gehe dabei wie folgt vor: \n",
|
||
"1. Wähle ein passendes **Farbschema**, um die einzelnen Klassenstufen anschaulich darzustellen. \n",
|
||
"2. Extrahiere die **Schlüssel** (Klassenstufen) und **Werte** (Anzahl der Schüler) aus dem Datenset und übergebe diese zusammen mit den Farbwerten an `plt.bar()`. \n",
|
||
"3. Setze geeignete Beschriftungen für die **X- und Y-Achse**, um die Darstellung verständlich zu machen. \n",
|
||
"4. Vergiss nicht, einen passenden **Titel** für den Plot zu setzen. \n",
|
||
"5. Gib den Plot mit `plt.show()` aus, um die Werte zu visualisieren."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 49,
|
||
"id": "0608b1ea-6275-47c7-82a8-fed86e5e5973",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-b954e989a8bbc2fa",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"sec_school = {\n",
|
||
" '5. Klasse': 29,\n",
|
||
" '6. Klasse': 35,\n",
|
||
" '7. Klasse': 25,\n",
|
||
" '8. Klasse': 28,\n",
|
||
" '9. Klasse': 31\n",
|
||
"}"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 50,
|
||
"id": "ae63d6f9-cd8c-4603-9a15-7ee336d905e9",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-8caba57a6ad34b87",
|
||
"locked": false,
|
||
"points": 5,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAjIAAAHHCAYAAACle7JuAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAATP5JREFUeJzt3Xl8THf////nJJFJRBJCiBBBbLW1tdWeEoSiVdRSV2traYsuul26WNuii+rVqmp9Sqt2tfTSoopYSnvZVS0NpfalVBJBkLx/f/SX+RpJmGFicvRxv93mdjNneZ/XvM85k6ezjc0YYwQAAGBBPt4uAAAA4EYRZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZP7hJk+eLJvNpv379zuG3Xvvvbr33nu9VpOnDR06VDabLc+3ebMSEhJks9mUkJDg7VJwDaVLl1abNm082ubtts+6I7vvMLhuypQpqlSpkvLly6eCBQt6u5wbQpDxoPvvv1/58+dXSkpKjtN069ZN/v7+OnXq1E0v78iRIxo6dKi2bNly021ZTeaX14YNG5yGJyUlqU6dOgoICNDixYu9VB2udO+996pq1arZjtu/f79sNpvefffdW1xV9v7J+1RekhnK58yZ4zT84sWLatOmjXx8fPT55597qbq8Ydq0aRo7duxNtbFr1y716NFDMTEx+uyzz/Tpp596prhbjCDjQd26ddP58+c1b968bMefO3dOCxYsUMuWLVW4cOGbXt6RI0c0bNiwm/rSfeSRR3T+/HlFR0ffdD3elpycrBYtWmjbtm2aN2+eWrZsKUl67bXXdP78eS9Xl/saN26s8+fPq3Hjxt4uxbI8sU8hd1y6dEkdO3bUd999p88++0y9evXydkle5Ykgk5CQoIyMDH3wwQfq0aOHOnXq5JnibjGCjAfdf//9Cg4O1rRp07Idv2DBAqWmpqpbt243tZzLly/r4sWLN9VGJl9fXwUEBOS50yTuSklJUXx8vLZs2aKvv/5arVq1cozz8/NTQECAF6u7vnPnzt10Gz4+PgoICJCPz63drTMyMnThwoVbukzkXRcuXFBGRoZH27x06ZI6deqkhQsXasKECerdu7dH2/+nOnHihCRZ9pRSJoKMBwUGBqp9+/ZatmyZYwO50rRp0xQcHKz7779fknTmzBk9++yzioqKkt1uV7ly5TR69GinL4ErD72PHTtWMTExstvt+vjjj1W7dm1JUs+ePWWz2WSz2TR58mTHvD///LNatmyp0NBQ5c+fX7Gxsfrxxx+danLl/HJO02R3TUbmaYQdO3aoSZMmyp8/v0qUKKG33347S7t//PGH7r//fgUFBalo0aJ67rnntGTJErev8zh79qxatmypTZs26euvv1br1q2dxmd3PYvNZlP//v01f/58Va1aVXa7XVWqVMn2dNSaNWtUu3ZtBQQEKCYmRhMmTMixlq+++ko1a9ZUYGCgwsLC1KVLFx08eNBpmsw+2rhxoxo3bqz8+fPrlVdeueZn3LVrlzp27KiwsDAFBASoVq1a+uabb5ymudn1kZaWpiFDhqhcuXKy2+2KiorSSy+9pLS0tGz7burUqapSpYrsdrtHT+OdPn1aL7zwgqpVq6YCBQooJCRErVq10tatW52mu5HtcuPGjapfv74CAwNVpkwZffLJJ07zXWufSkxMVIcOHRQREaGAgACVLFlSXbp0UVJSktPyv/rqK9WpU0f58+dXoUKF1LhxY33//fdZPueaNWscp0HLli2rL7/80ml8TtdhuXpNiKvrMzuu9Jf0//p6xowZeu2111SiRAnlz59fycnJkqTZs2c79ociRYroX//6lw4fPnzd5V/p8uXL6tKlixYsWKDx48fr8ccfv+48CxYsUOvWrRUZGSm73a6YmBiNGDFC6enpTtO5sk6XLl2qhg0bqmDBgipQoIAqVqyYZX91d9+53vdOSkqKnn32WZUuXVp2u11FixZV8+bNtWnTJkl/r59vv/1Wf/zxh2M7LV26tCTX94vSpUtryJAhkqTw8HDZbDYNHTrUMf2iRYvUqFEjBQUFKTg4WK1bt9avv/563b73Bj9vF3C76datm7744gvNmjVL/fv3dww/ffq0lixZoq5duyowMFDnzp1TbGysDh8+rL59+6pUqVJau3atBg0apKNHj2Y5ZDhp0iRduHBBffr0kd1u14MPPqiUlBQNHjxYffr0UaNGjSRJ9evXlyQtX75crVq1Us2aNTVkyBD5+Pho0qRJatq0qVavXq06derkWh/89ddfatmypdq3b69OnTppzpw5evnll1WtWjXHkZLU1FQ1bdpUR48e1TPPPKOIiAhNmzZNK1ascGtZqampatWqldavX685c+a4dRHlmjVrNHfuXD311FMKDg7Wf/7zH3Xo0EEHDhxwnPr75Zdf1KJFC4WHh2vo0KG6fPmyhgwZomLFimVp780339Trr7+uTp066bHHHtPJkyf14YcfqnHjxtq8ebPT/3pOnTqlVq1aqUuXLvrXv/6VbXuZfv31VzVo0EAlSpTQv//9bwUFBWnWrFlq166dvv76az344IPX/JyurI+MjAzdf//9WrNmjfr06aM77rhDv/zyi95//3399ttvmj9/vlOby5cvd2zjRYoUcXyJ5iQ9PV1//vlntrVd7ffff9f8+fP10EMPqUyZMjp+/LgmTJig2NhY7dixQ5GRkddc1rX64b777lOnTp3UtWtXzZo1S08++aT8/f3Vq1cv3XHHHRo+fHi2+9TFixcVHx+vtLQ0DRgwQBERETp8+LAWLlyoM2fOKDQ0VJI0bNgwDR06VPXr19fw4cPl7++vn3/+WcuXL1eLFi0ctezZs0cdO3ZU79691b17d33++efq0aOHatasqSpVqtzQ57uSu+vzRvrrSiNGjJC/v79eeOEFpaWlyd/fX5MnT1bPnj1Vu3ZtjRw5UsePH9cHH3ygH3/8Mcv+kJPLly+ra9eumjdvnsaNG6e+ffu69PknT56sAgUKaODAgSpQoICWL1+uwYMHKzk5We+8844kubROf/31V7Vp00bVq1fX8OHDZbfbtWfPHqf/ELrb16587zzxxBOaM2eO+vfvr8qVK+vUqVNas2aNdu7cqRo1aujVV19VUlKSDh06pPfff1+SVKBAAZf6JtPYsWP15Zdfat68eRo/frwKFCig6tWrS/r7AuDu3bsrPj5eo0eP1rlz5zR+/Hg1bNhQmzdvvu7+fssZeNTly5dN8eLFTb169ZyGf/LJJ0aSWbJkiTHGmBEjRpigoCDz22+/OU3373//2/j6+poDBw4YY4zZt2+fkWRCQkLMiRMnnKZdv369kWQmTZrkNDwjI8OUL1/exMfHm4yMDMfwc+fOmTJlypjmzZs7hk2aNMlIMvv27XMMi42NNbGxsdecxhhjVqxYYSSZFStWOM0ryXz55ZeOYWlpaSYiIsJ06NDBMey9994zksz8+fMdw86fP28qVaqUpc3sZNYUHR1t8uXL59TO1YYMGWKu3tQlGX9/f7Nnzx7HsK1btxpJ5sMPP3QMa9eunQkICDB//PGHY9iOHTuMr6+vU5v79+83vr6+5s0333Razi+//GL8/Pychmf20SeffHLNz5gpLi7OVKtWzVy4cMExLCMjw9SvX9+UL1/eMexm1seUKVOMj4+PWb16tdOyM7fbH3/80TFMkvHx8TG//vqrS/Vn1nCt1zvvvOOY/sKFCyY9Pd2pjX379hm73W6GDx/uGHYj2+V7773n1A933XWXKVq0qLl48aIxJud9avPmzUaSmT17do6fMzEx0fj4+JgHH3wwS/1X7ofR0dFGklm1apVj2IkTJ4zdbjfPP/+8Y1h2221On/vqfdad9ZkdV/srs6/Lli1rzp0755j24sWLpmjRoqZq1arm/PnzjuELFy40kszgwYOvufzMdjP7aty4cTlOm11/XFlLpr59+5r8+fM79iNX1un7779vJJmTJ0/mOI27+44r3zuhoaGmX79+OS7TGGNat25toqOjswx3Z7/I3Mau/HwpKSmmYMGC5vHHH3ea/9ixYyY0NDTL8LyAU0se5uvrqy5dumjdunVOh/amTZumYsWKKS4uTtLfh1wbNWqkQoUK6c8//3S8mjVrpvT0dK1atcqp3Q4dOig8PNylGrZs2aLExEQ9/PDDOnXqlKPt1NRUxcXFadWqVR4/h32lAgUK6F//+pfjvb+/v+rUqaPff//dMWzx4sUqUaKE4zSbJAUEBLh02PhKx48fV0BAgKKiotyus1mzZoqJiXG8r169ukJCQhx1pqena8mSJWrXrp1KlSrlmO6OO+5QfHy8U1tz585VRkaGOnXq5LQ+IyIiVL58+SxHmux2u3r27HndGk+fPq3ly5erU6dOSklJcbR76tQpxcfHKzEx8bqH6l1ZH7Nnz9Ydd9yhSpUqOdXftGlTScpSf2xsrCpXrnzd+jOVLl1aS5cuzfL66quvskxrt9sd1/mkp6fr1KlTjkP6mYfWb4Sfn5/T/+j9/f3Vt29fnThxQhs3brzmvJlHXJYsWZLj9Uzz589XRkaGBg8enOU6patPEVWuXNlxxEf6+9B+xYoVndbJzXB3fWbHnf7q3r27AgMDHe83bNigEydO6KmnnnK6Pq1169aqVKmSvv32W5c+x/Hjx+Xn56cyZcq4NH2mK2vJ3G8aNWqkc+fOadeuXZJcW6eZR40WLFiQ43emu319ve+dzOX+/PPPOnLkiFuf2xOWLl2qM2fOqGvXrk6fx9fXV/fcc4/bR81vBYJMLsi8mDfzot9Dhw5p9erV6tKli3x9fSX9fW528eLFCg8Pd3o1a9ZMkrJcY+POjpyYmCjp7y+Xq9ufOHGi0tLSspzX96SSJUtm+eIuVKiQ02mEP/74QzExMVmmK1eunFvLmjBhgvz9/dWyZUvt3r3brXmvDCfZ1Xny5EmdP39e5cuXzzJdxYoVnd4nJibKGKPy5ctn6fOdO3dmWZ8lSpSQv7//dWvcs2ePjDF6/fXXs7SbeX47u+uxruTK+khMTNSvv/6aZRkVKlTIdhnu/mEJCgpSs2bNsrwaNGiQZdqMjAy9//77Kl++vOx2u4oUKaLw8HBt27btprbbyMhIBQUFOQ3L/HzXu96kTJkyGjhwoCZOnKgiRYooPj5e48aNc6pn79698vHxcSngXW/bu1nurs/suNNfV28Pf/zxh6Ss+4kkVapUyTH+et5++22VKlVKHTt2zHJ937X8+uuvevDBBxUaGqqQkBCFh4c7wnzmOnNlnXbu3FkNGjTQY489pmLFiqlLly6aNWuWU6hxt69dWfdvv/22tm/frqioKNWpU0dDhw71WMi9nsy/H02bNs3ymb7//nuXtp1bjWtkckHNmjVVqVIlTZ8+Xa+88oqmT58uY4zT3UoZGRlq3ry5XnrppWzbyNwJMl35P4zrydzJ3nnnHd11113ZTuPO+dSc7mi6+sK5TJlh7WrGGJeX6arKlSvru+++U1xcnJo3b64ff/zR5aMznqwzIyNDNptNixYtyrbdq/vb1fWZuS5feOGFLEeBMl0v/LnyOTMyMlStWjWNGTMm22mv7lN3tkd3vfXWW3r99dfVq1cvjRgxQmFhYfLx8dGzzz7r9AfE3e3yZr333nvq0aOHFixYoO+//15PP/20Ro4cqZ9++kklS5Z0qy1X1snNfD531+fNyq3toXjx4o6LbVu3bq2VK1fqzjvvvOY8Z86cUWxsrEJCQjR8+HDFxMQoICBAmzZt0ssvv+y0DV1vnQYGBmrVqlVasWKFvv32Wy1evFgzZ85U06ZN9f3338vX19ftvnZl3Xfq1EmNGjXSvHnz9P333+udd97R6NGjNXfuXKc7MrNzs/tFZv9MmTJFERERWcb7+eW92JD3KrpNdOvWTa+//rq2bdumadOmqXz58o47IiQpJiZGZ8+edRyBuRE5bbCZhy1DQkJuqv1MhQoVkvT3F8SVXP1fVXaio6O1Y8cOGWOcPseePXvcbqtOnTqaP3++WrdurebNm2v16tUun4a7lvDwcAUGBjr+h3Klq4/+xMTEyBijMmXKZAmhN6Ns2bKSpHz58nlkXeYkJiZGW7duVVxcnNdvxZ8zZ46aNGmi//u//3MafubMGRUpUsTx3t3t8siRI0pNTXU6yvDbb79JkuPixet99mrVqqlatWp67bXXtHbtWjVo0ECffPKJ3njjDcXExCgjI0M7duzI8T8Q7rjy8115Yawr+50n1qcr/ZWTzOdS7d6923GKJdPu3bvdem5V2bJltWTJEsXGxio+Pl6rV6/O9ihppoSEBJ06dUpz5851eqbSvn37sp3+WutU+vuxBnFxcYqLi9OYMWP01ltv6dVXX9WKFSscp4lyY98pXry4nnrqKT311FM6ceKEatSooTfffNMRZHJa1s1+X2f+/ShatGiufud4EqeWcknm0ZfBgwdry5YtWZ4d06lTJ61bt05LlizJMu+ZM2d0+fLl6y4j8wvm6g22Zs2aiomJ0bvvvquzZ89mme/kyZOufgxJ/2/DvvK6nfT09Jt6CmR8fLwOHz7sdAvxhQsX9Nlnn91Qe3FxcZo+fbr27Nmjli1bOm7/vBm+vr6Kj4/X/PnzdeDAAcfwnTt3Zllv7du3l6+vr4YNG5bliI4x5oaf5Fy0aFHde++9mjBhgo4ePZplvLvrMiedOnXS4cOHs+3/8+fPKzU11SPLcYWvr2+WPpw9e3aWa4Hc3S4vX77sdOv8xYsXNWHCBIWHh6tmzZqSct6nkpOTs+yT1apVk4+Pj+MW23bt2snHx0fDhw/Pcj3FjRzly+7zpaam6osvvrjuvJ5Yn670V05q1aqlokWL6pNPPnG6BXnRokXauXNnlkckXE+1atX07bff6uzZs2revPk1rwvLPOJxZZ9fvHhRH3/8sdN0rqzT06dPZ2k/M6RmTuPpfSc9PT3LKdSiRYsqMjLSqS+DgoKyPdV6s9/X8fHxCgkJ0VtvvaVLly5lGe+p7xxP4ohMLilTpozq16+vBQsWSFKWIPPiiy/qm2++UZs2bRy3XaampuqXX37RnDlztH//fqf/fWYnJiZGBQsW1CeffKLg4GAFBQXpnnvuUZkyZTRx4kS1atVKVapUUc+ePVWiRAkdPnxYK1asUEhIiP773/+6/FmqVKmiunXratCgQTp9+rTCwsI0Y8YMl8JWTvr27auPPvpIXbt21TPPPKPixYtr6tSpjgsDb+R/Ng8++KDjiZ/333+/Fi9efNMPwhs2bJgWL16sRo0a6amnntLly5f14YcfqkqVKtq2bZtjupiYGL3xxhsaNGiQ9u/fr3bt2ik4OFj79u3TvHnz1KdPH73wwgs3VMO4cePUsGFDVatWTY8//rjKli2r48ePa926dTp06FCW56vciEceeUSzZs3SE088oRUrVqhBgwZKT0/Xrl27NGvWLC1ZskS1atW66eW4ok2bNho+fLh69uyp+vXr65dfftHUqVMdR6cyubtdRkZGavTo0dq/f78qVKigmTNnasuWLfr000+VL18+STnvU1u3blX//v310EMPqUKFCrp8+bKmTJkiX19fdejQQdLfp/heffVVjRgxQo0aNVL79u1lt9u1fv16RUZGauTIkW71Q4sWLVSqVCn17t1bL774onx9ffX5558rPDzcKVhnxxPr05X+ykm+fPk0evRo9ezZU7Gxseratavj9uvSpUvrueeec6svJKlevXqaO3eu2rZt6zjymt0T0uvXr69ChQqpe/fuevrpp2Wz2TRlypQsYXL58uXXXafDhw/XqlWr1Lp1a0VHR+vEiRP6+OOPVbJkSTVs2FCS5/edlJQUlSxZUh07dtSdd96pAgUK6IcfftD69ev13nvvOaarWbOmZs6cqYEDB6p27doqUKCA2rZte9Pf1yEhIRo/frweeeQR1ahRQ126dHFsc99++60aNGigjz76yOXPc0vc+hul/jnGjRtnJJk6depkOz4lJcUMGjTIlCtXzvj7+5siRYqY+vXrm3fffddxe2Pm7ddX3p56pQULFpjKlSsbPz+/LLeNbt682bRv394ULlzY2O12Ex0dbTp16mSWLVvmmMaVWzmNMWbv3r2mWbNmxm63m2LFiplXXnnFLF26NNvbXKtUqZKlzu7du2e5VfD33383rVu3NoGBgSY8PNw8//zz5uuvvzaSzE8//ZTt57267vXr12cZ9+677xpJpk2bNubSpUs53n6d3e2N0dHRpnv37k7DVq5caWrWrGn8/f1N2bJlzSeffJLjrbFff/21adiwoQkKCjJBQUGmUqVKpl+/fmb37t2OaXLqo2vZu3evefTRR01ERITJly+fKVGihGnTpo2ZM2eOY5qcbjt2dX1cvHjRjB492lSpUsXY7XZTqFAhU7NmTTNs2DCTlJTkmC6nvsvJtT5vdtv3hQsXzPPPP2+KFy9uAgMDTYMGDcy6des8sl1u2LDB1KtXzwQEBJjo6Gjz0UcfZakpu33q999/N7169TIxMTEmICDAhIWFmSZNmpgffvghy/yff/65ufvuux19GBsba5YuXeoYHx0dbVq3bp1tP139+TZu3Gjuuece4+/vb0qVKmXGjBnj8j7r6vrMjqv9lbnN5XQL88yZMx19ERYWZrp162YOHTp0zWVfr92ZM2caHx8fU7t2bZOcnJxtf/z444+mbt26JjAw0ERGRpqXXnrJLFmyxGm7cGWdLlu2zDzwwAMmMjLS+Pv7m8jISNO1a9csj8242X3nyu+dtLQ08+KLL5o777zTBAcHm6CgIHPnnXeajz/+2Gmes2fPmocfftgULFjQcat6Jlf3i+xuv75yHcTHx5vQ0FATEBBgYmJiTI8ePcyGDRuyTOttNmNy4QpM4AaNHTtWzz33nA4dOqQSJUp4uxzcJu699179+eef2r59u7dLsQT6C1bCNTLwmqt/yPHChQuaMGGCypcvT4gBALiEa2TgNe3bt1epUqV01113KSkpSV999ZV27dqlqVOners0AIBFEGTgNfHx8Zo4caKmTp2q9PR0Va5cWTNmzFDnzp29XRoAwCK4RgYAAFgW18gAAADLIsgAAADLuu2vkcnIyNCRI0cUHBzs9UevAwAA1xhjlJKSosjIyCy/KH+l2z7IHDlyxOM/kAYAAG6NgwcPXvOHWW/7IBMcHCzp744ICQnxcjUAAMAVycnJioqKcvwdz8ltH2QyTyeFhIQQZAAAsJjrXRbCxb4AAMCyCDIAAMCyCDIAAMCyCDIAAMCyCDIAAMCyCDIAAMCyCDIAAMCyCDIAAMCyCDIAAMCyCDIAAMCyvBpkxo8fr+rVqzt+PqBevXpatGiRY/y9994rm83m9HriiSe8WDEAAMhLvPpbSyVLltSoUaNUvnx5GWP0xRdf6IEHHtDmzZtVpUoVSdLjjz+u4cOHO+bJnz+/t8oFAAB5jFeDTNu2bZ3ev/nmmxo/frx++uknR5DJnz+/IiIivFEeAADI4/LMNTLp6emaMWOGUlNTVa9ePcfwqVOnqkiRIqpataoGDRqkc+fOebFKAACQl3j1iIwk/fLLL6pXr54uXLigAgUKaN68eapcubIk6eGHH1Z0dLQiIyO1bds2vfzyy9q9e7fmzp2bY3tpaWlKS0tzvE9OTs71zwAAALzDZowx3izg4sWLOnDggJKSkjRnzhxNnDhRK1eudISZKy1fvlxxcXHas2ePYmJism1v6NChGjZsWJbhSUlJCgkJ8Xj9uPVsNm9XYC3e3cMB4MYkJycrNDT0un+/vR5krtasWTPFxMRowoQJWcalpqaqQIECWrx4seLj47OdP7sjMlFRUQSZ2whBxj15aw8HANe4GmS8fmrpahkZGU5B5EpbtmyRJBUvXjzH+e12u+x2e26UBgAA8hivBplBgwapVatWKlWqlFJSUjRt2jQlJCRoyZIl2rt3r6ZNm6b77rtPhQsX1rZt2/Tcc8+pcePGql69ujfLBgAAeYRXg8yJEyf06KOP6ujRowoNDVX16tW1ZMkSNW/eXAcPHtQPP/ygsWPHKjU1VVFRUerQoYNee+01b5YMAADykDx3jYynuXqODdbBNTLuub33cAC3K1f/fueZ58gAAAC4iyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsiyADAAAsy8/bBQAAkOes3ODtCqwjtpZXF88RGQAAYFkEGQAAYFkEGQAAYFkEGQAAYFkEGQAAYFleDTLjx49X9erVFRISopCQENWrV0+LFi1yjL9w4YL69eunwoULq0CBAurQoYOOHz/uxYoBAEBe4tUgU7JkSY0aNUobN27Uhg0b1LRpUz3wwAP69ddfJUnPPfec/vvf/2r27NlauXKljhw5ovbt23uzZAAAkIfYjDHG20VcKSwsTO+88446duyo8PBwTZs2TR07dpQk7dq1S3fccYfWrVununXrutRecnKyQkNDlZSUpJCQkNwsHbeIzebtCqwlb+3hgEXwHBnX5dJzZFz9+51nrpFJT0/XjBkzlJqaqnr16mnjxo26dOmSmjVr5pimUqVKKlWqlNatW5djO2lpaUpOTnZ6AQCA25PXg8wvv/yiAgUKyG6364knntC8efNUuXJlHTt2TP7+/ipYsKDT9MWKFdOxY8dybG/kyJEKDQ11vKKionL5EwAAAG/xepCpWLGitmzZop9//llPPvmkunfvrh07dtxwe4MGDVJSUpLjdfDgQQ9WCwAA8hKv/9aSv7+/ypUrJ0mqWbOm1q9frw8++ECdO3fWxYsXdebMGaejMsePH1dERESO7dntdtnt9twuGwAA5AFePyJztYyMDKWlpalmzZrKly+fli1b5hi3e/duHThwQPXq1fNihQAAIK/w6hGZQYMGqVWrVipVqpRSUlI0bdo0JSQkaMmSJQoNDVXv3r01cOBAhYWFKSQkRAMGDFC9evVcvmMJAADc3rwaZE6cOKFHH31UR48eVWhoqKpXr64lS5aoefPmkqT3339fPj4+6tChg9LS0hQfH6+PP/7YmyUDAIA8JM89R8bTeI7M7YfnyLjn9t7DgVzCc2Rcx3NkAAAAbgxBBgAAWBZBBgAAWJbXnyNjaVys4R4u1gAAeBhHZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGXxZF8AyNN4grjreHr4PxFHZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGURZAAAgGV5NciMHDlStWvXVnBwsIoWLap27dpp9+7dTtPce++9stlsTq8nnnjCSxUDAIC8xKtBZuXKlerXr59++uknLV26VJcuXVKLFi2UmprqNN3jjz+uo0ePOl5vv/22lyoGAAB5iZ83F7548WKn95MnT1bRokW1ceNGNW7c2DE8f/78ioiIuNXlAQCAPC5PXSOTlJQkSQoLC3MaPnXqVBUpUkRVq1bVoEGDdO7cuRzbSEtLU3JystMLAADcnrx6ROZKGRkZevbZZ9WgQQNVrVrVMfzhhx9WdHS0IiMjtW3bNr388svavXu35s6dm207I0eO1LBhw25V2cA/hm2YzdslWIYZYrxdAvCPYTPG5Ik97sknn9SiRYu0Zs0alSxZMsfpli9frri4OO3Zs0cxMTFZxqelpSktLc3xPjk5WVFRUUpKSlJISIhni7bxxe4WD21qdLt7PLWHE2Rc59kgQ7+7zoP9vnKD59q63cXWypVmk5OTFRoaet2/33niiEz//v21cOFCrVq16pohRpLuueceScoxyNjtdtnt9lypEwAA5C1eDTLGGA0YMEDz5s1TQkKCypQpc915tmzZIkkqXrx4LlcHAADyOq8GmX79+mnatGlasGCBgoODdezYMUlSaGioAgMDtXfvXk2bNk333XefChcurG3btum5555T48aNVb16dW+WDgAA8gCvBpnx48dL+vuhd1eaNGmSevToIX9/f/3www8aO3asUlNTFRUVpQ4dOui1117zQrUAACCv8fqppWuJiorSypUrb1E1AADAavLUc2QAAADcQZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACWRZABAACW5VaQuXTpkvz8/LR9+/bcqgcAAMBlbgWZfPnyqVSpUkpPT8+tegAAAFzm9qmlV199Va+88opOnz6dG/UAAAC4zM/dGT766CPt2bNHkZGRio6OVlBQkNP4TZs2eaw4AACAa3E7yLRr1y4XygAAAHCf20FmyJAhuVEHAACA227o9uszZ85o4sSJGjRokONamU2bNunw4cMeLQ4AAOBa3D4is23bNjVr1kyhoaHav3+/Hn/8cYWFhWnu3Lk6cOCAvvzyy9yoEwAAIAu3j8gMHDhQPXr0UGJiogICAhzD77vvPq1atcqjxQEAAFyL20Fm/fr16tu3b5bhJUqU0LFjxzxSFAAAgCvcDjJ2u13JyclZhv/2228KDw/3SFEAAACucDvI3H///Ro+fLguXbokSbLZbDpw4IBefvlldejQweMFAgAA5MTtIPPee+/p7NmzKlq0qM6fP6/Y2FiVK1dOwcHBevPNN3OjRgAAgGy5fddSaGioli5dqjVr1mjbtm06e/asatSooWbNmuVGfQAAADlyO8hkatiwoRo2bOjJWgAAANziUpD5z3/+43KDTz/99A0XAwAA4A6Xgsz777/v9P7kyZM6d+6cChYsKOnvJ/3mz59fRYsWJcgAAIBbxqWLffft2+d4vfnmm7rrrru0c+dOnT59WqdPn9bOnTtVo0YNjRgxIrfrBQAAcHD7rqXXX39dH374oSpWrOgYVrFiRb3//vt67bXXPFocAADAtbgdZI4eParLly9nGZ6enq7jx497pCgAAABXuB1k4uLi1LdvX23atMkxbOPGjXryySe5BRsAANxSbgeZzz//XBEREapVq5bsdrvsdrvq1KmjYsWKaeLEiblRIwAAQLbcfo5MeHi4vvvuO/3222/atWuXJKlSpUqqUKGCx4sDAAC4lht+IF6FChUILwAAwKvcDjLp6emaPHmyli1bphMnTigjI8Np/PLlyz1WHAAAwLW4HWSeeeYZTZ48Wa1bt1bVqlVls9lyoy4AAIDrcjvIzJgxQ7NmzdJ999130wsfOXKk5s6dq127dikwMFD169fX6NGjnZ5Rc+HCBT3//POaMWOG0tLSFB8fr48//ljFihW76eUDAABrc/uuJX9/f5UrV84jC1+5cqX69eunn376SUuXLtWlS5fUokULpaamOqZ57rnn9N///lezZ8/WypUrdeTIEbVv394jywcAANZmM8YYd2Z477339Pvvv+ujjz7y+GmlkydPqmjRolq5cqUaN26spKQkhYeHa9q0aerYsaMkadeuXbrjjju0bt061a1b97ptJicnKzQ0VElJSQoJCfFoveK0mnvc29RyRLe7x0PdLtswOt5VZoiHOl2SRL+7zoP9vnKD59q63cXWypVmXf377fappTVr1mjFihVatGiRqlSponz58jmNnzt3rvvV/v+SkpIkSWFhYZL+ftDepUuXnB60V6lSJZUqVcrlIAMAAG5fbgeZggUL6sEHH/R4IRkZGXr22WfVoEEDVa1aVZJ07Ngx+fv7O35lO1OxYsV07NixbNtJS0tTWlqa431ycrLHawUAAHmD20Fm0qRJuVGH+vXrp+3bt2vNmjU31c7IkSM1bNgwD1UFAADyMrcv9s0N/fv318KFC7VixQqVLFnSMTwiIkIXL17UmTNnnKY/fvy4IiIism1r0KBBSkpKcrwOHjyYm6UDAAAvcumITI0aNbRs2TIVKlRId9999zUv8r3yxySvxxijAQMGaN68eUpISFCZMmWcxtesWVP58uXTsmXL1KFDB0nS7t27deDAAdWrVy/bNjN//wkAANz+XAoyDzzwgCMctGvXzmML79evn6ZNm6YFCxYoODjYcd1LaGioAgMDFRoaqt69e2vgwIEKCwtTSEiIBgwYoHr16nGhLwAAcP3268uXL8vP79q5Z8eOHapcubLrC8/hyM6kSZPUo0cPSf/vgXjTp093eiBeTqeWrsbt13kIt197Bbdf33rcfu0t3H7tFVa5/bpbt26aOXNmjuN37Nihpk2b5ng3UXZcyVABAQEaN26cxo0b53K7AADgn8Hli33XrVunJ554IttxO3fuVNOmTVW/fn2PFQYAAHA9Lh+RWbJkiRo3bqywsDC99dZbjuG7du1S06ZNVbduXc2ePTtXigQAAMiOy0Hmjjvu0Hfffae4uDiFhYXphRde0K5du9SkSRPVrl1bc+bMka+vb27WCgAA4MStB+LVrl1b8+fPV5s2bXT27Fl99tlnqlmzpubMmXPdC4EBAAA8ze300bRpU02bNk0PPfSQWrRooXnz5mX5vSUAAIBbweUgU6hQoSy3S69evVrFihVzGnb69GnPVAYAAHAdLgeZsWPH5mIZAAAA7nM5yHTv3j036wAAAHBbnvjRSAAAgBtBkAEAAJZFkAEAAJZFkAEAAJZFkAEAAJbl0l1LAwcOdLnBMWPG3HAxAAAA7nApyGzevNmlxq5+YB4AAEBucinIrFixIrfrAAAAcBvXyAAAAMty+0cjU1NTNWrUKC1btkwnTpxQRkaG0/jff//dY8UBAABci9tB5rHHHtPKlSv1yCOPqHjx4lwXAwAAvMbtILNo0SJ9++23atCgQW7UAwAA4DK3r5EpVKiQwsLCcqMWAAAAt7gdZEaMGKHBgwfr3LlzuVEPAACAy1w6tXT33Xc7XQuzZ88eFStWTKVLl1a+fPmcpt20aZNnKwQAAMiBS0GmXbt2uVwGAACA+1wKMkOGDMntOgAAANzGA/EAAIBluX37dXp6ut5//33NmjVLBw4c0MWLF53Gnz592mPFAQAAXIvbR2SGDRumMWPGqHPnzkpKStLAgQPVvn17+fj4aOjQoblQIgAAQPbcDjJTp07VZ599pueff15+fn7q2rWrJk6cqMGDB+unn37KjRoBAACy5XaQOXbsmKpVqyZJKlCggJKSkiRJbdq00bfffuvZ6gAAAK7B7SBTsmRJHT16VJIUExOj77//XpK0fv162e12z1YHAABwDW4HmQcffFDLli2TJA0YMECvv/66ypcvr0cffVS9evXyeIEAAAA5cfuupVGjRjn+3blzZ0VHR2vt2rUqX7682rZt69HiAAAArsXtIHO1unXrqm7dup6oBQAAwC1un1ry9fVVkyZNsjwv5vjx4/L19fVYYQAAANfjdpAxxigtLU21atXSr7/+mmUcAADAreJ2kLHZbPr666/Vtm1b1atXTwsWLHAaBwAAcKvc0BEZX19fffDBB3r33XfVuXNnvfHGGxyNAQAAt9xNXezbp08flS9fXg899JBWrVrlqZoAAABc4vYRmejoaKeLeps0aaKffvpJBw8e9GhhAAAA1+N2kNm3b58KFy7sNKxcuXLavHmzfv/9d7faWrVqldq2bavIyEjZbDbNnz/faXyPHj1ks9mcXi1btnS3ZAAAcJu64VNLFy9e1IkTJ5SRkeEY5u7FvqmpqbrzzjvVq1cvtW/fPttpWrZsqUmTJjne8zMIAAAgk9tB5rffflPv3r21du1ap+HGGNlsNqWnp7vcVqtWrdSqVatrTmO32xUREeFumQAA4B/A7SDTs2dP+fn5aeHChSpevHiu33KdkJCgokWLqlChQmratKneeOONLKe2rpSWlqa0tDTH++Tk5FytDwAAeI/bQWbLli3auHGjKlWqlBv1OGnZsqXat2+vMmXKaO/evXrllVfUqlUrrVu3LsenCI8cOVLDhg3L9doAAID3uR1kKleurD///DM3asmiS5cujn9Xq1ZN1atXV0xMjBISEhQXF5ftPIMGDdLAgQMd75OTkxUVFZXrtQIAgFvP7buWRo8erZdeekkJCQk6deqUkpOTnV65qWzZsipSpIj27NmT4zR2u10hISFOLwAAcHty+4hMs2bNJCnLEZEbudjXXYcOHdKpU6dUvHjxXFsGAACwDreDzIoVKzy28LNnzzodXdm3b5+2bNmisLAwhYWFadiwYerQoYMiIiK0d+9evfTSSypXrpzi4+M9VgMAALAut4NMbGxsjuO2b9/uVlsbNmxQkyZNHO8zr23p3r27xo8fr23btumLL77QmTNnFBkZqRYtWmjEiBE8SwYAAEi6yd9akqSUlBRNnz5dEydO1MaNG906tXTvvfde88cmlyxZcrPlAQCA25jbF/tmWrVqlbp3767ixYvr3XffVdOmTfXTTz95sjYAAIBrcuuIzLFjxzR58mT93//9n5KTk9WpUyelpaVp/vz5qly5cm7VCAAAkC2Xj8i0bdtWFStW1LZt2zR27FgdOXJEH374YW7WBgAAcE0uH5FZtGiRnn76aT355JMqX758btYEAADgEpePyKxZs0YpKSmqWbOm7rnnHn300Ue37Am/AAAA2XE5yNStW1efffaZjh49qr59+2rGjBmKjIxURkaGli5dqpSUlNysEwAAIAu371oKCgpSr169tGbNGv3yyy96/vnnNWrUKBUtWlT3339/btQIAACQrRu+/VqSKlasqLfffluHDh3S9OnTPVUTAACAS24qyGTy9fVVu3bt9M0333iiOQAAAJd4JMgAAAB4A0EGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYFkEGAABYlleDzKpVq9S2bVtFRkbKZrNp/vz5TuONMRo8eLCKFy+uwMBANWvWTImJid4pFgAA5DleDTKpqam68847NW7cuGzHv/322/rPf/6jTz75RD///LOCgoIUHx+vCxcu3OJKAQBAXuTnzYW3atVKrVq1ynacMUZjx47Va6+9pgceeECS9OWXX6pYsWKaP3++unTpcitLBQAAeVCevUZm3759OnbsmJo1a+YYFhoaqnvuuUfr1q3Lcb60tDQlJyc7vQAAwO0pzwaZY8eOSZKKFSvmNLxYsWKOcdkZOXKkQkNDHa+oqKhcrRMAAHhPng0yN2rQoEFKSkpyvA4ePOjtkgAAQC7Js0EmIiJCknT8+HGn4cePH3eMy47dbldISIjTCwAA3J7ybJApU6aMIiIitGzZMsew5ORk/fzzz6pXr54XKwMAAHmFV+9aOnv2rPbs2eN4v2/fPm3ZskVhYWEqVaqUnn32Wb3xxhsqX768ypQpo9dff12RkZFq166d94oGAAB5hleDzIYNG9SkSRPH+4EDB0qSunfvrsmTJ+ull15Samqq+vTpozNnzqhhw4ZavHixAgICvFUyAADIQ2zGGOPtInJTcnKyQkNDlZSU5PnrZWw2z7Z3u/PQpka3u8dTe7htGB3vKjPEk1+r9LvrPNjvKzd4rq3bXWytXGnW1b/fefYaGQAAgOshyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMsiyAAAAMvK00Fm6NChstlsTq9KlSp5uywAAJBH+Hm7gOupUqWKfvjhB8d7P788XzIAALhF8nwq8PPzU0REhLfLAAAAeVCePrUkSYmJiYqMjFTZsmXVrVs3HThw4JrTp6WlKTk52ekFAABuT3k6yNxzzz2aPHmyFi9erPHjx2vfvn1q1KiRUlJScpxn5MiRCg0NdbyioqJuYcUAAOBWshljjLeLcNWZM2cUHR2tMWPGqHfv3tlOk5aWprS0NMf75ORkRUVFKSkpSSEhIZ4tyGbzbHu3Ow9tanS7ezy1h9uG0fGuMkM8+bVKv7vOg/2+coPn2rrdxdbKlWaTk5MVGhp63b/fef4amSsVLFhQFSpU0J49e3Kcxm63y26338KqAACAt+TpU0tXO3v2rPbu3avixYt7uxQAAJAH5Okg88ILL2jlypXav3+/1q5dqwcffFC+vr7q2rWrt0sDAAB5QJ4+tXTo0CF17dpVp06dUnh4uBo2bKiffvpJ4eHh3i4NAADkAXk6yMyYMcPbJQAAgDwsT59aAgAAuBaCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCyCDAAAsCxLBJlx48apdOnSCggI0D333KP//e9/3i4JAADkAXk+yMycOVMDBw7UkCFDtGnTJt15552Kj4/XiRMnvF0aAADwsjwfZMaMGaPHH39cPXv2VOXKlfXJJ58of/78+vzzz71dGgAA8LI8HWQuXryojRs3qlmzZo5hPj4+atasmdatW+fFygAAQF7g5+0CruXPP/9Uenq6ihUr5jS8WLFi2rVrV7bzpKWlKS0tzfE+KSlJkpScnJx7hcI1rAOv8Fi3X/BQO/8AfN94iwf7PfWs59q63eXS9p65Hxljrjldng4yN2LkyJEaNmxYluFRUVFeqAZOQkO9XcE/Et1+64WOotO9g36/HaWkpCj0Gl9keTrIFClSRL6+vjp+/LjT8OPHjysiIiLbeQYNGqSBAwc63mdkZOj06dMqXLiwbDZbrtabFyQnJysqKkoHDx5USEiIt8v5x6DfvYN+9w763Tv+af1ujFFKSooiIyOvOV2eDjL+/v6qWbOmli1bpnbt2kn6O5gsW7ZM/fv3z3Yeu90uu93uNKxgwYK5XGneExIS8o/Y0PMa+t076HfvoN+945/U79c6EpMpTwcZSRo4cKC6d++uWrVqqU6dOho7dqxSU1PVs2dPb5cGAAC8LM8Hmc6dO+vkyZMaPHiwjh07prvuukuLFy/OcgEwAAD458nzQUaS+vfvn+OpJDiz2+0aMmRIltNryF30u3fQ795Bv3sH/Z49m7nefU0AAAB5VJ5+IB4AAMC1EGQAAIBlEWQAAIBlEWRuAwkJCbLZbDpz5oy3S/lH2b9/v2w2m7Zs2eLtUv5R2N69g+3dO+j36yPI5KKhQ4fKZrM5vSpVquRWG9ltxCkpKWrSpIkqV66sQ4cOebjq28Phw4f1r3/9S4ULF1ZgYKCqVaumDRs2uNWGzWbT/PnzHe8vXbqkrl27qkSJEtq+fbuHK7a+0qVLZ9nebTab+vXr53IbbO/uS09P1+uvv64yZcooMDBQMTExGjFixHV/n+ZqbO/uSUlJ0bPPPqvo6GgFBgaqfv36Wr9+vdvt0O83zxK3X1tZlSpV9MMPPzje+/ndXJefPHlSrVq1ko+Pj1avXq3ChQtrz549N1vmbeWvv/5SgwYN1KRJEy1atEjh4eFKTExUoUKFbrjNc+fOqUOHDkpMTNSaNWtUpkwZ7d+/33NF3wbWr1+v9PR0x/vt27erefPmeuihh264Tbb36xs9erTGjx+vL774QlWqVNGGDRvUs2dPhYaG6umnn76hNtner++xxx7T9u3bNWXKFEVGRuqrr75Ss2bNtGPHDpUoUeKG2qTfbwxHZHKZn5+fIiIiHK8iRYrccFsHDx5Uo0aNFBoaquXLl6tw4cLZTnfq1ClHos+fP7+qVaum6dOnO00zZ84cVatWTYGBgSpcuLCaNWum1NRUSX8fuq9Tp46CgoJUsGBBNWjQQH/88Ydj3gULFqhGjRoKCAhQ2bJlNWzYMF2+fPmGP5enjR49WlFRUZo0aZLq1KmjMmXKqEWLFoqJibmh9s6cOaPmzZvryJEjji+X7KSnp6t3796O/xlXrFhRH3zwgdM01+rbrVu3qkmTJgoODlZISIhq1qzpdBRpzZo1atSokQIDAxUVFaWnn37asc7ygvDwcKdtfeHChYqJiVFsbOwNtcf27pq1a9fqgQceUOvWrVW6dGl17NhRLVq00P/+978bao/t/frOnz+vr7/+Wm+//bYaN26scuXKaejQoSpXrpzGjx9/Q23S7zeOIJPLEhMTFRkZqbJly6pbt246cODADbWze/duNWjQQJUrV9Z3332nAgUK5DjthQsXVLNmTX377bfavn27+vTpo0ceecTxxXb06FF17dpVvXr10s6dO5WQkKD27dvLGKPLly+rXbt2io2N1bZt27Ru3Tr16dPH8YObq1ev1qOPPqpnnnlGO3bs0IQJEzR58mS9+eabN/S5csM333yjWrVq6aGHHlLRokV1991367PPPruhto4dO+b4Q7xy5cocf6xU+vt3wEqWLKnZs2drx44dGjx4sF555RXNmjVLkq7bt926dVPJkiW1fv16bdy4Uf/+97+VL18+SdLevXvVsmVLdejQQdu2bdPMmTO1Zs2aPPugyIsXL+qrr75Sr169bujHWtneXVe/fn0tW7ZMv/32m6S//1CtWbNGrVq1crsttnfXXL58Wenp6QoICHAaHhgYqDVr1rjdHv1+kwxyzXfffWdmzZpltm7dahYvXmzq1atnSpUqZZKTk11uY9++fUaS8ff3N02aNDGXL1/OMs2KFSuMJPPXX3/l2E7r1q3N888/b4wxZuPGjUaS2b9/f5bpTp06ZSSZhISEbNuJi4szb731ltOwKVOmmOLFi7v8mXKb3W43drvdDBo0yGzatMlMmDDBBAQEmMmTJ7vVTma/V6pUyaSmpmYZn7luNm/enGMb/fr1Mx06dDDGXL9vg4ODc6yxd+/epk+fPk7DVq9ebXx8fMz58+dd/ES3zsyZM42vr685fPiwW/OxvbsvPT3dvPzyy8Zmsxk/Pz9js9my1OwKtnf31KtXz8TGxprDhw+by5cvmylTphgfHx9ToUIFt9qh328eQeYW+uuvv0xISIiZOHGiy/NkbsQdO3Y0fn5+ZtasWVmmufqL/fLly2b48OGmatWqplChQiYoKMj4+fmZhx56yDE+Li7OBAcHm44dO5pPP/3UnD592tFejx49jN1uN23atDFjx441R44ccYwrUqSICQgIMEFBQY5XQECAkZTtTugN+fLlM/Xq1XMaNmDAAFO3bl232pFk2rdvb3x8fMyYMWOyjM/uC+ajjz4yNWrUMEWKFDFBQUEmX758pnbt2o7x1+rbIUOGGD8/PxMXF2dGjhxp9uzZ4xhXq1Yt4+/v79Tv+fPnN5LMjh073Ppct0KLFi1MmzZt3J6P7d1906dPNyVLljTTp08327ZtM19++aUJCwu7oeDO9u66PXv2mMaNGxtJxtfX19SuXdt069bNVKpUya126PebR5C5xWrVqmX+/e9/uzz9lRvx8OHDjZ+fn5k5c6bTNFd/sY8cOdIULlzYTJkyxWzZssUkJiaa1q1bmwceeMAxT0ZGhlmzZo0ZPHiwqVatmgkPDze///67Y/ymTZvMW2+9ZerVq2cKFChg1q1bZ4wxJiAgwIwePdokJiZmeaWnp994x3hQqVKlTO/evZ2GffzxxyYyMtKtdiSZefPmmcmTJxsfHx/z3nvvOY2/+gtm+vTpJiAgwIwbN85s2rTJJCYmmj59+pg777zTab6c+tYYY3bv3m3GjBljmjdvbvz9/c3cuXONMcZUqlTJDBgwINt+T0tLc+tz5bb9+/cbHx8fM3/+fLfnZXt3X8mSJc1HH33kNGzEiBGmYsWKbrXD9n5jzp496wgKnTp1Mvfdd59b89PvN48gcwulpKSYQoUKmQ8++MDlea7eiN944w3j5+dnZsyY4Zjm6i/2Nm3amF69ejnGp6enm/Llyzt9sV/p8uXLpkSJEll2oEx169Y1AwYMMMYYU79+fae286KuXbuahg0bOg179tlnsxyluZ7MLxhjjPnyyy+Nr6+veeeddxzjr143/fv3N02bNnVqIy4uLssXzJWu7NurdenSxbRt29YYY8zDDz9s4uLi3KrfW4YMGWIiIiLMpUuX3J6X7d19YWFh5uOPP3Ya9tZbb5ny5cu71Q7b+805ffq0CQ0NNRMmTHBrPvr95nH7dS564YUX1LZtW0VHR+vIkSMaMmSIfH191bVrV8c0jz76qEqUKKGRI0e61Oarr74qX19fdevWTRkZGU5tZSpfvrzmzJmjtWvXqlChQhozZoyOHz+uypUrS5J+/vlnLVu2TC1atFDRokX1888/6+TJk7rjjju0b98+ffrpp7r//vsVGRmp3bt3KzExUY8++qgkafDgwWrTpo1KlSqljh07ysfHR1u3btX27dv1xhtveKDXbt5zzz2n+vXr66233lKnTp30v//9T59++qk+/fRTxzSDBg3S4cOH9eWXX7rU5iOPPCIfHx91795dxhi9+OKLWaYpX768vvzySy1ZskRlypTRlClTtH79esfdB9fq2/Pnz+vFF19Ux44dVaZMGR06dEjr169Xhw4dJEkvv/yy6tatq/79++uxxx5TUFCQduzYoaVLl+qjjz7yQK95RkZGhiZNmqTu3btn+6gBtnfPa9u2rd58802VKlVKVapU0ebNmzVmzBj16tXLMQ3bu+ctWbJExhhVrFhRe/bs0YsvvqhKlSqpZ8+ejmno91vEuznq9ta5c2dTvHhx4+/vb0qUKGE6d+7sdD7SGGNiY2NN9+7dc2wjpwu9Ro8ebXx9fc3UqVOz/A/11KlT5oEHHjAFChQwRYsWNa+99pp59NFHHf9D3bFjh4mPjzfh4eHGbrebChUqmA8//NAYY8yxY8dMu3btHHVHR0ebwYMHOx1GX7x4salfv74JDAw0ISEhpk6dOubTTz+96f7ypP/+97+matWqxm63m0qVKmWpr3v37iY2NvaabeiK/yllmjZtmvH19TWjRo3Ksm4uXLhgevToYUJDQ03BggXNk08+af797387/qd0rb5NS0szXbp0MVFRUcbf399ERkaa/v37O11g97///c80b97cFChQwAQFBZnq1aubN99882a7yqOWLFliJJndu3dnO57t3fOSk5PNM888Y0qVKmUCAgJM2bJlzauvvup0KoDt3fNmzpxpypYta/z9/U1ERITp16+fOXPmjNM09PutYTPGzcc/AgAA5BE8RwYAAFgWQQYAAFgWQQYAAFgWQQYAAFgWQQYAAFgWQQYAAFgWQQYAAFgWQQaA2+699149++yz3i7D6+bPn69y5crJ19eX/gC8hCADIIsePXqoXbt2TsPmzJmjgIAAvffee94pKpdk91ld1bdvX3Xs2FEHDx7UiBEjPFsYAJcQZABc18SJE9WtWzeNHz9ezz//vLfLyRPOnj2rEydOKD4+XpGRkQoODvZ2ScA/EkEGwDW9/fbbGjBggGbMmOH0g3hXmjJlimrVqqXg4GBFRETo4Ycf1okTJxzj//rrL3Xr1k3h4eEKDAxU+fLlNWnSJEnSxYsX1b9/fxUvXlwBAQGKjo52+lHJM2fO6LHHHlN4eLhCQkLUtGlTbd261TF+6NChuuuuuzRlyhSVLl1aoaGh6tKli1JSUhzTzJkzR9WqVVNgYKAKFy6sZs2aKTU1VUOHDtUXX3yhBQsWyGazyWazKSEhQQkJCbLZbDpz5oyjjS1btshms2n//v1KSEhwBJemTZs65pOkNWvWqFGjRgoMDFRUVJSefvpppaam3vR6AJA9ggyAHL388ssaMWKEFi5cqAcffDDH6S5duqQRI0Zo69atmj9/vvbv368ePXo4xr/++uvasWOHFi1apJ07d2r8+PEqUqSIJOk///mPvvnmG82aNUu7d+/W1KlTVbp0ace8Dz30kE6cOKFFixZp48aNqlGjhuLi4nT69GnHNHv37tX8+fO1cOFCLVy4UCtXrtSoUaMkSUePHlXXrl3Vq1cv7dy5UwkJCWrfvr2MMXrhhRfUqVMntWzZUkePHtXRo0dVv3796/ZL/fr1tXv3bknS119/7Zhv7969atmypTp06KBt27Zp5syZWrNmjfr37+9OtwNwh5d/tBJAHtS9e3fj7+9vJJlly5ZlGR8bG2ueeeaZHOdfv369kWRSUlKMMca0bdvW9OzZM9tpBwwYYJo2bWoyMjKyjFu9erUJCQkxFy5ccBoeExNjJkyYYIwxZsiQISZ//vwmOTnZMf7FF18099xzjzHGmI0bNxpJZv/+/Tl+1sxfys509S9sG2PM5s2bjSSzb98+Y4wxf/31l5FkVqxY4Zimd+/epk+fPlk+g4+Pj9MvDAPwHI7IAMhW9erVVbp0aQ0ZMkRnz5695rQbN25U27ZtVapUKQUHBys2NlaSdODAAUnSk08+qRkzZuiuu+7SSy+9pLVr1zrm7dGjh7Zs2aKKFSvq6aef1vfff+8Yt3XrVp09e1aFCxdWgQIFHK99+/Zp7969julKly7tdI1K8eLFHae27rzzTsXFxalatWp66KGH9Nlnn+mvv/66+Q7KxtatWzV58mSnWuPj45WRkaF9+/blyjKBfzqCDIBslShRQgkJCTp8+LBatmzpdM3JlVJTUxUfH6+QkBBNnTpV69ev17x58yT9ff2LJLVq1Up//PGHnnvuOR05ckRxcXF64YUXJEk1atTQvn37NGLECJ0/f16dOnVSx44dJf19QW3x4sW1ZcsWp9fu3bv14osvOmrIly+fU002m00ZGRmSJF9fXy1dulSLFi1S5cqV9eGHH6pixYrXDBY+Pn9/NRpjHMMuXbp03T47e/as+vbt61Tr1q1blZiYqJiYmOvOD8B9BBkAOYqOjtbKlSt17NixHMPMrl27dOrUKY0aNUqNGjVSpUqVnC70zRQeHq7u3bvrq6++0tixY/Xpp586xoWEhKhz58767LPPNHPmTH399dc6ffq0atSooWPHjsnPz0/lypVzemVeY+MKm82mBg0aaNiwYdq8ebP8/f0dYcvf31/p6elZapX+vr4m05YtW667nBo1amjHjh1Zai1Xrpz8/f1drheA6wgyAK4pKipKCQkJjluNk5OTncaXKlVK/v7++vDDD/X777/rm2++yfJMlcGDB2vBggXas2ePfv31Vy1cuFB33HGHJGnMmDGaPn26du3apd9++02zZ89WRESEChYsqGbNmqlevXpq166dvv/+e+3fv19r167Vq6++qg0bNrhU/88//6y33npLGzZs0IEDBzR37lydPHnSsfzSpUtr27Zt2r17t/78809dunRJ5cqVU1RUlIYOHarExER9++23Lj0/5+WXX9batWvVv39/bdmyRYmJiVqwYAEX+wK5iCAD4LpKliyphIQE/fnnn1nCTHh4uCZPnqzZs2ercuXKGjVqlN59912n+f39/TVo0CBVr15djRs3lq+vr2bMmCFJCg4O1ttvv61atWqpdu3a2r9/v7777jv5+PjIZrPpu+++U+PGjdWzZ09VqFBBXbp00R9//KFixYq5VHtISIhWrVql++67TxUqVNBrr72m9957T61atZIkPf7446pYsaJq1aql8PBw/fjjj8qXL58jXFWvXl2jR4/WG2+8cd1lVa9eXStXrtRvv/2mRo0a6e6779bgwYMVGRnpalcDcJPNXHkSGAAAwEI4IgMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACyLIAMAACzr/wM5NKfMEs+oEQAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"colors = [\"red\", \"blue\", \"green\", \"yellow\", \"pink\"]\n",
|
||
"plt.bar(sec_school.keys(), sec_school.values(), color=colors)\n",
|
||
"plt.xlabel(\"Klassenstufe\")\n",
|
||
"plt.ylabel(\"Anzahl Kinder\")\n",
|
||
"plt.title(\"Verteilung Kinder einer Hauptschule pro Klassenstufe\")\n",
|
||
"plt.show()\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "bf9e917c-6949-4bb1-8184-270747e8cb4e",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-42bf44a09515d0fd",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Horizontales Bar Chart\n",
|
||
"\n",
|
||
"Analog zum klassischen Bar Chart erzeugt `plt.barh` ein **horizontales Balkendiagramm**. \n",
|
||
"\n",
|
||
"Dieses Format eignet sich besonders, wenn die Kategorienamen länger sind oder die horizontale Darstellung die Lesbarkeit verbessert. \n",
|
||
"\n",
|
||
"Beispiel:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 51,
|
||
"id": "146615f7-1315-41a3-a690-73c98ee465e3",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-54166820b406e29e",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAl8AAAGwCAYAAACXRQDXAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAANNtJREFUeJzt3XtYVXXe///XBuQk7C2iJngAylOWmuKYyNcxEiXTlMzDMKZZmc6EjebVZIyp2VTawVK7uxs7jNrMeMrxMKNjya2ApngW0lQ0U2ASxRsTBBME1u8Pf+579kAObLdrIz4f17Wvy73WZ3/We+3PNLyuz/qstS2GYRgCAACAKTzcXQAAAMDthPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIm83F0AHFVWVur06dMKDAyUxWJxdzkAAKAGDMPQxYsXFRoaKg+P689tEb7qmNOnT6tVq1buLgMAADghNzdXLVu2vG4bwlcdExgYKOnq4FmtVjdXAwAAaqKoqEitWrWy/x2/HsJXHXPtUqPVaiV8AQBwi6nJkiEW3AMAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiL3cXgOrNttnk6+4iAACoZ2YahrtLYOYLAADATIQvAAAAExG+AAAATET4AgAAMBHhCwAAwESELwAAABMRvgAAAExE+AIAADAR4QsAAMBEhC8AAAATEb4AAABMRPgCAAAwEeELAADARIQvAAAAExG+AAAATET4AgAAMBHhCwAAwESELwAAABMRvgAAAExE+AIAADAR4QsAAMBEhC8AAAATEb4AAABMRPgCAAAwEeELAADARIQvAAAAExG+AAAATET4AgAAMBHhCwAAwESELwAAABPdFuErNTVVFotFFy5ccHcpAADgNldnwtecOXNksVg0efLkWn3u1KlTslgsysjIsG+7ePGiYmJi1LFjR/3zn/90baEAAAA3oE6Erz179mjhwoXq3LnzDfd17tw5xcTEqKSkRNu2bVPLli1dUCEAAIBruD18FRcXa9SoUfr4448VFBR0Q33l5uaqd+/estls2rJli4KDg6ttV1BQoISEBLVo0UL+/v7q1KmTli1b5tBm1apV6tSpk/z8/BQcHKzY2FiVlJRIunoZs0ePHmrYsKEaNWqk6OhoZWdn2z+7bt06devWTb6+vrrzzjs1a9YslZeXV1tLaWmpioqKHF4AAKD+cnv4SkxM1MCBAxUbG3tD/WRlZSk6OlodO3bUP/7xDwUEBPxk28uXLysyMlIbNmzQoUOHNH78eI0ePVq7d++WJOXl5SkhIUFPPfWUjhw5otTUVA0dOlSGYai8vFzx8fHq06ePvv76a6Wnp2v8+PGyWCySpG3btmnMmDGaNGmSDh8+rIULF2rx4sV6/fXXq61l9uzZstls9lerVq1u6HsAAAB1m8UwDMNdB1++fLlef/117dmzR76+vnrggQd03333ad68eTXu49SpU4qIiJC3t7eio6OVnJwsT09PhzapqamKiYnRDz/8oEaNGlXbz6BBg9ShQwe988472r9/vyIjI3Xq1CmFhYU5tDt//ryCg4OVmpqqPn36VOknNjZWffv2VVJSkn3bn//8Z7344os6ffp0lfalpaUqLS21vy8qKlKrVq30kiTfGn8LAACgJmbepNhTVFQkm82mwsJCWa3W67b1uikV1EBubq4mTZqk5ORk+freeMwYPHiw1q5dq9WrV2v48OHXbVtRUaE33nhDK1eu1Pfff6+ysjKVlpbK399fktSlSxf17dtXnTp1UlxcnPr3769hw4YpKChIjRs31tixYxUXF6d+/fopNjZWI0aMUEhIiCQpMzNT27dvd5jpqqio0OXLl3Xp0iX7Ma7x8fGRj4/PDZ8/AAC4NbjtsuO+ffuUn5+vbt26ycvLS15eXkpLS9OCBQvk5eWlioqKWvU3bdo0zZgxQ7/85S+1cuXK67Z9++23NX/+fE2dOlUpKSnKyMhQXFycysrKJEmenp5KTk7Wxo0b1bFjR73//vtq3769Tp48KUlatGiR0tPT1atXL61YsULt2rXTzp07JV1dwzZr1ixlZGTYXwcPHtTx48ddEjIBAMCtzW0zX3379tXBgwcdtj355JPq0KGDpk6dWuXSYU1Mnz5dHh4eGjVqlAzD0MiRI6ttt337dg0ZMkSPP/64JKmyslLHjh1Tx44d7W0sFouio6MVHR2tGTNmKCwsTGvWrNGUKVMkSV27dlXXrl2VlJSkqKgoLV26VD179lS3bt2UlZWlNm3a1Lp+AABQ/7ktfAUGBuree+912NawYUMFBwc7bB8zZoxatGih2bNn16jfadOmydPTU6NGjVJlZaUSEhKqtGnbtq1WrVqlHTt2KCgoSO+++67Onj1rD1+7du3S5s2b1b9/fzVr1ky7du3SuXPndPfdd+vkyZP66KOPNHjwYIWGhiorK0vHjx/XmDFjJEkzZszQoEGD1Lp1aw0bNkweHh7KzMzUoUOH9Nprrzn7dQEAgHrCbeGrpnJycuThUburoy+99JI8PDw0evRoGYah0NBQh/0vv/yyvvvuO8XFxcnf31/jx49XfHy8CgsLJUlWq1Vbt27VvHnzVFRUpLCwMM2dO1cDBgzQ2bNndfToUS1ZskQFBQUKCQlRYmKiJkyYIEmKi4vT+vXr9eqrr+rNN99UgwYN1KFDB40bN841XwgAALilufVuR1R17W4J7nYEAMD16sLdjm5/zhcAAMDthPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJvJydwGoXlJhoaxWq7vLAAAALsbMFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiL3cXgOrNttnk6+4iANySZhqGu0sAcB3MfAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgotsifKWmpspisejChQvuLgUAANzm3Bq+PvzwQ3Xu3FlWq1VWq1VRUVHauHFjrfo4deqULBaLMjIy7NsuXryomJgYdezYUf/85z9dXDUAAIDz3Bq+WrZsqTlz5mjfvn3au3evHnzwQQ0ZMkTffPON032eO3dOMTExKikp0bZt29SyZUsXVgwAAHBj3Bq+HnnkET388MNq27at2rVrp9dff10BAQHauXOnU/3l5uaqd+/estls2rJli4KDg6ttV1BQoISEBLVo0UL+/v7q1KmTli1b5tBm1apV6tSpk/z8/BQcHKzY2FiVlJRIunoZs0ePHmrYsKEaNWqk6OhoZWdn2z+7bt06devWTb6+vrrzzjs1a9YslZeXO3VOAACgfvFydwHXVFRU6PPPP1dJSYmioqJq/fmsrCz99re/Vffu3bVs2TL5+Pj8ZNvLly8rMjJSU6dOldVq1YYNGzR69Gjddddd6tGjh/Ly8pSQkKC33npLjz76qC5evKht27bJMAyVl5crPj5ezzzzjJYtW6aysjLt3r1bFotFkrRt2zaNGTNGCxYsUO/evXXixAmNHz9ekjRz5swqtZSWlqq0tNT+vqioqNbnDgAAbh0WwzAMZz54/PhxpaSkKD8/X5WVlQ77ZsyYUeN+Dh48qKioKF2+fFkBAQFaunSpHn744Rp//tSpU4qIiJC3t7eio6OVnJwsT09PhzapqamKiYnRDz/8oEaNGlXbz6BBg9ShQwe988472r9/vyIjI3Xq1CmFhYU5tDt//ryCg4OVmpqqPn36VOknNjZWffv2VVJSkn3bn//8Z7344os6ffp0lfavvPKKZs2aVWX7S5J8a3D+APDvZjr3f+sAbkBRUZFsNpsKCwtltVqv29ap8PXxxx/r17/+tZo0aaLmzZvbZ30kyWKxaP/+/TXuq6ysTDk5OSosLNSqVav0ySefKC0tTR07dqzR56+Fr2HDhmnt2rVaunSphg8f7tDm38NXRUWF3njjDa1cuVLff/+9ysrKVFpaqkcffVQrV65URUWF4uLitHv3bsXFxal///4aNmyYgoKCJElPPvmkli1bpn79+ik2NlYjRoxQSEiIJKlp06YqLi52CIAVFRW6fPmySkpK5O/v71BbdTNfrVq1InwBcBrhCzDfTQ9fYWFhevbZZzV16lSni/wpsbGxuuuuu7Rw4cIatb8Wvg4cOKC///3vevXVV/WXv/xFI0aMsLf59/A1Z84cvfPOO5o3b546deqkhg0bavLkyfLy8tLatWslSYZhaMeOHdq0aZPWrFmjM2fOaNeuXYqIiJAkHThwQF988YX+/ve/6+DBg0pOTlbPnj3l5+enWbNmaejQoVVqvfPOO+Xhcf1ldtcGj/AFwFmEL8B8tQlfTq35+uGHH6rMLrlKZWWlw0xQbUyfPl0eHh4aNWqUDMPQyJEjq223fft2DRkyRI8//rj9mMeOHXOYbbNYLIqOjlZ0dLRmzJihsLAwrVmzRlOmTJEkde3aVV27dlVSUpKioqK0dOlS9ezZU926dVNWVpbatGnj1DkAAID6zanwNXz4cG3atEm/+tWvbujgSUlJGjBggFq3bq2LFy9q6dKlSk1N1ZdffmlvM2bMGLVo0UKzZ8+uUZ/Tpk2Tp6enRo0apcrKSiUkJFRp07ZtW61atUo7duxQUFCQ3n33XZ09e9Yevnbt2qXNmzerf//+atasmXbt2qVz587p7rvv1smTJ/XRRx9p8ODBCg0NVVZWlo4fP64xY8ZIurrebdCgQWrdurWGDRsmDw8PZWZm6tChQ3rttddu6PsCAAC3PqfCV5s2bTR9+nTt3LlTnTp1UoMGDRz2/+Y3v6lRP/n5+RozZozy8vJks9nUuXNnffnll+rXr5+9TU5Ozn+8VPfvXnrpJXl4eGj06NEyDEOhoaEO+19++WV99913iouLk7+/v8aPH6/4+HgVFhZKkqxWq7Zu3ap58+apqKhIYWFhmjt3rgYMGKCzZ8/q6NGjWrJkiQoKChQSEqLExERNmDBBkhQXF6f169fr1Vdf1ZtvvqkGDRqoQ4cOGjduXK3OAQAA1E9Orfm6tu6p2g4tFn333Xc3VNTtjDVfAG4Ua74A8930NV8nT550qjAAAIDb3Q094b6srExZWVk8vR0AAKCGnApfly5d0tNPPy1/f3/dc889ysnJkSQ999xzmjNnjksLBAAAqE+cCl9JSUnKzMxUamqqfH3/b2VSbGysVqxY4bLiAAAA6hun1nytXbtWK1asUM+ePR2ebn/PPffoxIkTLisOAACgvnFq5uvcuXNq1qxZle0lJSUOYQwAAACOnApf3bt314YNG+zvrwWuTz75RFFRUa6pDAAAoB5y6rLjG2+8oQEDBujw4cMqLy/X/PnzdfjwYe3YsUNpaWmurhEAAKDecGrm6//9v/+njIwMlZeXq1OnTtq0aZOaNWum9PR0RUZGurpGAACAeqPGM19TpkzR73//ezVs2FBbt25Vr1699PHHH9/M2gAAAOqdGs98vf/++youLpYkxcTE6Pz58zetKAAAgPqqxjNf4eHhWrBggfr37y/DMJSenq6goKBq2/785z93WYEAAAD1SY1/WHvt2rX61a9+pfz8fFksFv3UxywWiyoqKlxa5O2EH9YGcKP4YW3AfDflh7Xj4+MVHx+v4uJiWa1WZWVlVfusLwAAAPy0Wj9qIiAgQCkpKYqIiJCXl1NPqgAAALhtOZWeIiIidPr06Z/c37p1a6cLAgAAqM+cCl/h4eHX/Rkh1nwBAABUz6nwdeDAAYf3V65c0YEDB/Tuu+/q9ddfd0lhAAAA9ZFT4atLly5VtnXv3l2hoaF6++23NXTo0BsuDAAAoD5y6ueFfkr79u21Z88eV3YJAABQrzg181VUVOTw3jAM5eXl6ZVXXlHbtm1dUhgAAEB95FT4atSoUZUF94ZhqFWrVlq+fLlLCgMAAKiPnApfKSkpDu89PDzUtGlTtWnThmd/AQAAXIdTSclisahXr15VglZ5ebm2bt3KbzsCAAD8BKcW3MfExOj8+fNVthcWFiomJuaGiwIAAKivnApfhmFU+5DVgoICNWzY8IaLAgAAqK9qddnx2vO7LBaLxo4dKx8fH/u+iooKff311+rVq5drKwQAAKhHahW+bDabpKszX4GBgfLz87Pv8/b2Vs+ePfXMM8+4tkIAAIB6pFbha9GiRZKu/rbjCy+8wCXGmyipsFBWq9XdZQAAABdzas3Xiy++6LDmKzs7W/PmzdOmTZtcVhgAAEB95FT4GjJkiD777DNJ0oULF9SjRw/NnTtXQ4YM0YcffujSAgEAAOoTp8LX/v371bt3b0nSqlWr1Lx5c2VnZ+uzzz7TggULXFogAABAfeJU+Lp06ZICAwMlSZs2bdLQoUPl4eGhnj17Kjs726UFAgAA1CdOha82bdpo7dq1ys3N1Zdffqn+/ftLkvLz81kkDgAAcB1Oha8ZM2bohRdeUHh4uO6//35FRUVJujoL1rVrV5cWCAAAUJ9YDMMwnPngmTNnlJeXpy5dusjD42qG2717t6xWqzp06ODSIm8nRUVFstlsKuRREwAA3DJq8/fbqR/WlqTmzZurefPmDtt69OjhbHcAAAC3BafCV0lJiebMmaPNmzcrPz9flZWVDvu/++47lxQHAABQ3zgVvsaNG6e0tDSNHj1aISEh1f7INgAAAKpyKnxt3LhRGzZsUHR0tKvrAQAAqNecutsxKChIjRs3dnUtAAAA9Z5T4ev3v/+9ZsyYoUuXLrm6HgAAgHrNqcuOc+fO1YkTJ3THHXcoPDxcDRo0cNi/f/9+lxQHAABQ3zgVvuLj411cBgAAwO3B6Yes4ubgIasAANx6avP326k1X5J04cIFffLJJ0pKStL58+clXb3c+P333zvbJQAAQL3n1GXHr7/+WrGxsbLZbDp16pSeeeYZNW7cWKtXr1ZOTo4+++wzV9d525lts8nX3UUAwE00kwsvuE05NfM1ZcoUjR07VsePH5ev7/9FhIcfflhbt251WXEAAAD1jVPha8+ePZowYUKV7S1atNCZM2duuCgAAID6yqnw5ePjo6Kioirbjx07pqZNm95wUQAAAPWVU+Fr8ODBevXVV3XlyhVJksViUU5OjqZOnarHHnvMpQUCAADUJ06Fr7lz56q4uFjNmjXTjz/+qD59+qhNmzYKDAzU66+/7uoaAQAA6g2n7na02WxKTk7W9u3blZmZqeLiYnXr1k2xsbGurg8AAKBecSp8XRMdHa3o6GhJV5/7BQAAgOtz6rLjm2++qRUrVtjfjxgxQsHBwWrRooUyMzNdVhwAAEB941T4+sMf/qBWrVpJkpKTk5WcnKyNGzdqwIAB+u1vf+vSAgEAAOoTpy47njlzxh6+1q9frxEjRqh///4KDw/X/fff79ICAQAA6hOnZr6CgoKUm5srSfriiy/sC+0Nw1BFRYXrqgMAAKhnnJr5Gjp0qH75y1+qbdu2Kigo0IABAyRJBw4cUJs2bVxaIAAAQH3iVPh67733FB4ertzcXL311lsKCAiQJOXl5enZZ591aYEAAAD1icUw+Fn5uqSoqEg2m00vSfL9j60B4NY1kz8/qEeu/f0uLCyU1Wq9blun1nwtWbJEGzZssL9/8cUX1ahRI/Xq1UvZ2dnOdAkAAHBbcCp8vfHGG/Lz85Mkpaen64MPPtBbb72lJk2a6Pnnn3dpgQAAAPWJU2u+cnNz7Qvr165dq8cee0zjx49XdHS0HnjgAVfWBwAAUK84NfMVEBCggoICSdKmTZvUr18/SZKvr69+/PFH11UHAABQzzg189WvXz+NGzdOXbt21bFjx/Twww9Lkr755huFh4e7sj4AAIB6xamZrw8++EBRUVE6d+6c/vrXvyo4OFiStG/fPiUkJLi0QAAAgPqER03UMTxqAsDtgkdNoD6pzaMmnLrseM2lS5eUk5OjsrIyh+2dO3e+kW4BAADqLafC17lz5zR27Fh98cUX1e7n9x0BAACq59Sar8mTJ6uwsFC7du2Sn5+fvvjiCy1ZskRt27bV3/72N1fXCAAAUG84NfO1ZcsWrVu3Tt27d5eHh4fCwsLUr18/Wa1WzZ49WwMHDnR1nQAAAPWCUzNfJSUlatasmSQpKChI586dkyR16tRJ+/fvd111AAAA9YxT4at9+/bKysqSJHXp0kULFy7U999/rz/84Q8KCQlxaYEAAAD1iVOXHSdNmqS8vDxJ0syZM/XQQw/pL3/5i7y9vbV48WJX1gcAAFCvOBW+Hn/8cfu/IyMjlZ2draNHj6p169Zq0qSJy4oDAACob27oOV/X+Pv7q1u3bq7oCgAAoF6rcfiaMmVKjTt99913nSrmZklNTVVMTIx++OEHNWrUyN3lAACA21iNw9eBAwdq1O7ixYs1Pvjs2bO1evVqHT16VH5+furVq5fefPNNtW/fvsZ9nDp1ShERETpw4IDuu+8+ew2DBw/W2bNntWnTphr3BQAAcLPVOHylpKTovffe0/PPP/+TbS5evKiHHnqoxgdPS0tTYmKifvazn6m8vFy/+93v1L9/fx0+fFgNGzascT//6ty5cxowYIA8PDy0bds2BQcH69tvv3WqLwAAAFer1aMmfve73+mzzz6rdl9JSYkGDBiggoKCGvf3xRdfaOzYsbrnnnvUpUsXLV68WDk5Odq3b19tyrLLzc1V7969ZbPZtGXLFgUHB1fbrqCgQAkJCWrRooX8/f3VqVMnLVu2zKHNqlWr1KlTJ/n5+Sk4OFixsbEqKSmRdPUyZo8ePdSwYUM1atRI0dHRys7Otn923bp16tatm3x9fXXnnXdq1qxZKi8vr7aW0tJSFRUVObwAAED9Vavw9ac//UkTJkyo8hNCxcXFiouLU35+vrZs2eJ0MYWFhZKkxo0b1/qzWVlZio6OVseOHfWPf/xDAQEBP9n28uXLioyM1IYNG3To0CGNHz9eo0eP1u7duyVJeXl5SkhI0FNPPaUjR44oNTVVQ4cOlWEYKi8vV3x8vPr06aOvv/5a6enpGj9+vCwWiyRp27ZtGjNmjCZNmqTDhw9r4cKFWrx4sV5//fVqa5k9e7ZsNpv91apVq1qfOwAAuHVYDMMwavOBTz75RJMmTdKGDRv0wAMPqKSkRA899JDOnDmjtLQ0hYaGOlVIZWWlBg8erAsXLuirr76q8eeurfny9vZWdHS0kpOT5enp6dCmJgvuBw0apA4dOuidd97R/v37FRkZqVOnTiksLMyh3fnz5xUcHKzU1FT16dOnSj+xsbHq27evkpKS7Nv+/Oc/68UXX9Tp06ertC8tLVVpaan9fVFRkVq1aqWXJPnW+FsAgFvPzNr9+QHqtKKiItlsNhUWFspqtV63ba0fNTFu3DidP39eQ4YM0bp16zRjxgydPn36hoKXJCUmJurQoUO1Cl7/avDgwVq7dq1Wr16t4cOHX7dtRUWF3njjDa1cuVLff/+9ysrKVFpaKn9/f0lXn9rft29fderUSXFxcerfv7+GDRumoKAgNW7cWGPHjlVcXJz69eun2NhYjRgxwv5k/8zMTG3fvt1hpquiokKXL1/WpUuX7Me4xsfHRz4+Pk6dMwAAuPU49fNCL774on7961+rb9+++v7775WamqqWLVs6XcTEiRO1fv16paSkON3PtGnTNGPGDP3yl7/UypUrr9v27bff1vz58zV16lSlpKQoIyNDcXFxKisrkyR5enoqOTlZGzduVMeOHfX++++rffv2OnnypCRp0aJFSk9PV69evbRixQq1a9dOO3fulHT1EuysWbOUkZFhfx08eFDHjx+Xry9zWQAA3O5qNfM1dOhQh/cNGjRQkyZNNGnSJIftq1evrlF/hmHoueee05o1a5SamqqIiIjalFPF9OnT5eHhoVGjRskwDI0cObLadtu3b9eQIUPsT+qvrKzUsWPH1LFjR3sbi8Wi6OhoRUdHa8aMGQoLC9OaNWvszzvr2rWrunbtqqSkJEVFRWnp0qXq2bOnunXrpqysLLVp0+aGzgUAANRPtQpfNpvN4X1CQsINHTwxMVFLly7VunXrFBgYqDNnztiP4+fnJ0kaM2aMWrRoodmzZ9eoz2nTpsnT01OjRo1SZWVltTW2bdtWq1at0o4dOxQUFKR3331XZ8+etYevXbt2afPmzerfv7+aNWumXbt26dy5c7r77rt18uRJffTRRxo8eLBCQ0OVlZWl48ePa8yYMZKkGTNmaNCgQWrdurWGDRsmDw8PZWZm6tChQ3rttddu6PsCAAC3vlqFr0WLFrn04B9++KEk6YEHHqhynLFjx0qScnJy5OFRu6ujL730kjw8PDR69GgZhlFlLdrLL7+s7777TnFxcfL399f48eMVHx9vv9vSarVq69atmjdvnoqKihQWFqa5c+dqwIABOnv2rI4ePaolS5aooKBAISEhSkxM1IQJEyRJcXFxWr9+vV599VW9+eabatCggTp06KBx48Y58Q0BAID6ptZ3O+Lmuna3BHc7AqjvuNsR9Ult7nZ0asE9AAAAnEP4AgAAMBHhCwAAwESELwAAABMRvgAAAExE+AIAADAR4QsAAMBEhC8AAAATEb4AAABMRPgCAAAwEeELAADARIQvAAAAExG+AAAATET4AgAAMBHhCwAAwESELwAAABMRvgAAAExE+AIAADAR4QsAAMBEhC8AAAATEb4AAABMRPgCAAAwEeELAADARIQvAAAAExG+AAAATET4AgAAMBHhCwAAwESELwAAABN5ubsAVC+psFBWq9XdZQAAABdj5gsAAMBEhC8AAAATEb4AAABMRPgCAAAwEeELAADARIQvAAAAExG+AAAATET4AgAAMBHhCwAAwESELwAAABMRvgAAAExE+AIAADAR4QsAAMBEhC8AAAATEb4AAABMRPgCAAAwkZe7C0D1Ztts8nV3EQAAuNhMw3B3CW7HzBcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJrotwtepU6dksViUkZHh7lIAAMBtzq3ha+vWrXrkkUcUGhoqi8WitWvXOtXPv3/2ypUrSkhIUIsWLXTo0CHXFAsAAOACbg1fJSUl6tKliz744AOX9Xnp0iUNHjxYe/bs0VdffaV7773XZX0DAADcKLeGrwEDBui1117To48+6pL+Lly4oH79+un06dP66quvFBERUW27iooKPf3004qIiJCfn5/at2+v+fPnO7RJTU1Vjx491LBhQzVq1EjR0dHKzs6WJGVmZiomJkaBgYGyWq2KjIzU3r177Z/96quv1Lt3b/n5+alVq1b6zW9+o5KSEpecIwAAuLV5ubsAVzlz5oz69OmjgIAApaWlqVGjRj/ZtrKyUi1bttTnn3+u4OBg7dixQ+PHj1dISIhGjBih8vJyxcfH65lnntGyZctUVlam3bt3y2KxSJJGjRqlrl276sMPP5Snp6cyMjLUoEEDSdKJEyf00EMP6bXXXtMf//hHnTt3ThMnTtTEiRO1aNGiKrWUlpaqtLTU/r6oqMi1XwwAAKhTLIZhGO4uQrq6bmvNmjWKj4936rPe3t668847tW/fPvn7+zvsP3XqlCIiInTgwAHdd9991fYxceJEnTlzRqtWrdL58+cVHBys1NRU9enTp0pbq9Wq999/X0888USVfePGjZOnp6cWLlxo3/bVV1+pT58+Kikpka+vr0P7V155RbNmzarSz0uSfKtsBQDg1jazbsQOlysqKpLNZlNhYaGsVut129abux0HDRqkY8eOOYSe6/nggw8UGRmppk2bKiAgQB999JFycnIkSY0bN9bYsWMVFxenRx55RPPnz1deXp79s1OmTNG4ceMUGxurOXPm6MSJE/Z9mZmZWrx4sQICAuyvuLg4VVZW6uTJk1XqSEpKUmFhof2Vm5t7g98EAACoy+pN+Bo9erT++Mc/6oUXXtC777573bbLly/XCy+8oKefflqbNm1SRkaGnnzySZWVldnbLFq0SOnp6erVq5dWrFihdu3aaefOnZKuzlZ98803GjhwoLZs2aKOHTtqzZo1kqTi4mJNmDBBGRkZ9ldmZqaOHz+uu+66q0otPj4+slqtDi8AAFB/1Zs1X5L0xBNPyMPDQ08++aQqKyv1wgsvVNtu+/bt6tWrl5599ln7tn+dvbqma9eu6tq1q5KSkhQVFaWlS5eqZ8+ekqR27dqpXbt2ev7555WQkKBFixbp0UcfVbdu3XT48GG1adPm5pwkAAC4pbl15qu4uNg+OyRJJ0+eVEZGhv3yn3T1styYMWNq3Ofo0aO1ZMkSvfTSS3r77berbdO2bVvt3btXX375pY4dO6bp06drz5499v0nT55UUlKS0tPTlZ2drU2bNun48eO6++679eOPP2rixIlKTU1Vdna2tm/frj179ujuu++WJE2dOlU7duzQxIkTlZGRoePHj2vdunWaOHGiE98QAACob9w687V3717FxMTY30+ZMkXS1RmsxYsXS5Ly8vIcwlhNjBo1Sh4eHho9erQqKys1cuRIh/0TJkzQgQMHNHLkSFksFiUkJOjZZ5/Vxo0bJUn+/v46evSolixZooKCAoWEhCgxMVETJkxQeXm5CgoKNGbMGJ09e1ZNmjTR0KFD7YvmO3furLS0NE2bNk29e/eWYRi66667qtQAAABuT3Xmbkdcde1uCe52BADUR9ztWI8W3AMAANwKCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIi93F4DqJRUWymq1ursMAADgYsx8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAmInwBAACYiPAFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIm83F0AHBmGIUkqKipycyUAAKCmrv3dvvZ3/HoIX3VMQUGBJKlVq1ZurgQAANTWxYsXZbPZrtuG8FXHNG7cWJKUk5PzHwcP7lFUVKRWrVopNzdXVqvV3eWgGoxR3ccY1X2MUe0YhqGLFy8qNDT0P7YlfNUxHh5Xl+HZbDb+x17HWa1WxqiOY4zqPsao7mOMaq6mkyYsuAcAADAR4QsAAMBEhK86xsfHRzNnzpSPj4+7S8FPYIzqPsao7mOM6j7G6OaxGDW5JxIAAAAuwcwXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCVx3zwQcfKDw8XL6+vrr//vu1e/dud5d029q6daseeeQRhYaGymKxaO3atQ77DcPQjBkzFBISIj8/P8XGxur48ePuKfY2NHv2bP3sZz9TYGCgmjVrpvj4eGVlZTm0uXz5shITExUcHKyAgAA99thjOnv2rJsqvv18+OGH6ty5s/0hnVFRUdq4caN9P+NT98yZM0cWi0WTJ0+2b2OcXI/wVYesWLFCU6ZM0cyZM7V//3516dJFcXFxys/Pd3dpt6WSkhJ16dJFH3zwQbX733rrLS1YsEB/+MMftGvXLjVs2FBxcXG6fPmyyZXentLS0pSYmKidO3cqOTlZV65cUf/+/VVSUmJv8/zzz+vvf/+7Pv/8c6Wlpen06dMaOnSoG6u+vbRs2VJz5szRvn37tHfvXj344IMaMmSIvvnmG0mMT12zZ88eLVy4UJ07d3bYzjjdBAbqjB49ehiJiYn29xUVFUZoaKgxe/ZsN1YFwzAMScaaNWvs7ysrK43mzZsbb7/9tn3bhQsXDB8fH2PZsmVuqBD5+fmGJCMtLc0wjKvj0aBBA+Pzzz+3tzly5IghyUhPT3dXmbe9oKAg45NPPmF86piLFy8abdu2NZKTk40+ffoYkyZNMgyD/45uFma+6oiysjLt27dPsbGx9m0eHh6KjY1Venq6GytDdU6ePKkzZ844jJfNZtP999/PeLlJYWGhpP/7cfp9+/bpypUrDmPUoUMHtW7dmjFyg4qKCi1fvlwlJSWKiopifOqYxMREDRw40GE8JP47uln4Ye064n//939VUVGhO+64w2H7HXfcoaNHj7qpKvyUM2fOSFK143VtH8xTWVmpyZMnKzo6Wvfee6+kq2Pk7e2tRo0aObRljMx18OBBRUVF6fLlywoICNCaNWvUsWNHZWRkMD51xPLly7V//37t2bOnyj7+O7o5CF8AbnmJiYk6dOiQvvrqK3eXgn/Tvn17ZWRkqLCwUKtWrdITTzyhtLQ0d5eF/19ubq4mTZqk5ORk+fr6uruc2waXHeuIJk2ayNPTs8odJGfPnlXz5s3dVBV+yrUxYbzcb+LEiVq/fr1SUlLUsmVL+/bmzZurrKxMFy5ccGjPGJnL29tbbdq0UWRkpGbPnq0uXbpo/vz5jE8dsW/fPuXn56tbt27y8vKSl5eX0tLStGDBAnl5eemOO+5gnG4Cwlcd4e3trcjISG3evNm+rbKyUps3b1ZUVJQbK0N1IiIi1Lx5c4fxKioq0q5duxgvkxiGoYkTJ2rNmjXasmWLIiIiHPZHRkaqQYMGDmOUlZWlnJwcxsiNKisrVVpayvjUEX379tXBgweVkZFhf3Xv3l2jRo2y/5txcj0uO9YhU6ZM0RNPPKHu3burR48emjdvnkpKSvTkk0+6u7TbUnFxsb799lv7+5MnTyojI0ONGzdW69atNXnyZL322mtq27atIiIiNH36dIWGhio+Pt59Rd9GEhMTtXTpUq1bt06BgYH29Sc2m01+fn6y2Wx6+umnNWXKFDVu3FhWq1XPPfecoqKi1LNnTzdXf3tISkrSgAED1Lp1a128eFFLly5VamqqvvzyS8anjggMDLSvk7ymYcOGCg4Otm9nnG4Cd99uCUfvv/++0bp1a8Pb29vo0aOHsXPnTneXdNtKSUkxJFV5PfHEE4ZhXH3cxPTp04077rjD8PHxMfr27WtkZWW5t+jbSHVjI8lYtGiRvc2PP/5oPPvss0ZQUJDh7+9vPProo0ZeXp77ir7NPPXUU0ZYWJjh7e1tNG3a1Ojbt6+xadMm+37Gp27610dNGAbjdDNYDMMw3JT7AAAAbjus+QIAADAR4QsAAMBEhC8AAAATEb4AAABMRPgCAAAwEeELAADARIQvAAAAExG+AAAATET4AgAnvfLKK7rvvvuu2+aBBx7Q5MmTb/pxaiI8PFzz5s274X4A3BjCF4BbVnp6ujw9PTVw4EB3l+K0xYsXq1GjRg7bjhw5olatWmn48OEqKyvTCy+84PDDxgBubYQvALesTz/9VM8995y2bt2q06dPu7scl9izZ4969+6thx56SCtWrJC3t7cCAgIUHBzs7tJUVlbm7hKAeoHwBeCWVFxcrBUrVujXv/61Bg4cqMWLFzvsT01NlcVi0ebNm9W9e3f5+/urV69eysrKsrcJDw+XxWKp8rpm6tSpateunfz9/XXnnXdq+vTpunLlSpVa/vSnPyk8PFw2m02/+MUvdPHiRafOacuWLXrwwQf19NNP6+OPP5aHx9X/i/73y45jx45VfHy83nnnHYWEhCg4OFiJiYkOteXn5+uRRx6Rn5+fIiIi9Je//KXK8S5cuKBx48apadOmslqtevDBB5WZmWnff+24n3zyiSIiIuTr6+vUeQFwRPgCcEtauXKlOnTooPbt2+vxxx/XH//4RxmGUaXdtGnTNHfuXO3du1deXl566qmn7Pv27NmjvLw85eXl6Z///Kd69uyp3r172/cHBgZq8eLFOnz4sObPn6+PP/5Y7733nkP/J06c0Nq1a7V+/XqtX79eaWlpmjNnTq3PZ82aNRo4cKBefvllvfnmm/+xfUpKik6cOKGUlBQtWbJEixcvdgigY8eOVW5urlJSUrRq1Sr993//t/Lz8x36GD58uPLz87Vx40bt27dP3bp1U9++fXX+/Hl7m2+//VZ//etftXr1amVkZNT6vABUwwCAW1CvXr2MefPmGYZhGFeuXDGaNGlipKSk2PenpKQYkoz/+Z//sW/bsGGDIcn48ccfq/T3m9/8xggLCzPy8/N/8phvv/22ERkZaX8/c+ZMw9/f3ygqKrJv++1vf2vcf//99vd9+vQxJk2a9JN9Llq0yPD09DQ8PT2N6dOnV9tm5syZRpcuXezvn3jiCSMsLMwoLy+3bxs+fLgxcuRIwzAMIysry5Bk7N69277/yJEjhiTjvffeMwzDMLZt22ZYrVbj8uXLDse66667jIULF9qP26BBg+t+JwBqj5kvALecrKws7d69WwkJCZIkLy8vjRw5Up9++mmVtp07d7b/OyQkRJKqzAB99NFH+vTTT/W3v/1NTZs2tW9fsWKFoqOj1bx5cwUEBOjll19WTk6Ow2fDw8MVGBjocIx/7/8/8fPzU79+/fTxxx/ryJEjNfrMPffcI09Pz2qPe+TIEXl5eSkyMtK+v0OHDg4L+zMzM1VcXKzg4GAFBATYXydPntSJEyfs7cLCwhy+EwA3zsvdBQBAbX366acqLy9XaGiofZthGPLx8dF//dd/yWaz2bc3aNDA/u9r67kqKyvt21JSUvTcc89p2bJlDkEtPT1do0aN0qxZsxQXFyebzably5dr7ty5DrX8a//XjvGv/deEp6en1q5dq6FDhyomJkYpKSm6++67r/uZGz1ucXGxQkJClJqaWmXfv4a0hg0b1rhPADVD+AJwSykvL9dnn32muXPnqn///g774uPjtWzZMv3qV7+qUV/ffvuthg0bpt/97ncaOnSow74dO3YoLCxM06ZNs2/Lzs6+8RP4CT4+Plq9erWGDRummJgYbdmyRR07dnSqrw4dOqi8vFz79u3Tz372M0lXZwsvXLhgb9OtWzedOXNGXl5eCg8Pd8EZAKgpLjsCuKWsX79eP/zwg55++mnde++9Dq/HHnus2kuP1fnxxx/1yCOPqGvXrho/frzOnDljf0lS27ZtlZOTo+XLl+vEiRNasGCB1qxZczNPTT4+PvrrX/+q+++/XzExMfrmm2+c6qd9+/Z66KGHNGHCBO3atUv79u3TuHHj5OfnZ28TGxurqKgoxcfHa9OmTTp16pR27NihadOmae/eva46JQDVIHwBuKV8+umnio2Ndbi0eM1jjz2mvXv36uuvv/6P/Zw9e1ZHjx7V5s2bFRoaqpCQEPtLkgYPHqznn39eEydO1H333acdO3Zo+vTpLj+ff+ft7a1Vq1apV69eiomJ0aFDh5zqZ9GiRQoNDVWfPn00dOhQjR8/Xs2aNbPvt1gs+sc//qGf//znevLJJ9WuXTv94he/UHZ2tu644w5XnQ6AalgMo5p7swEAAHBTMPMFAABgIsIXAACAiQhfAAAAJiJ8AQAAmIjwBQAAYCLCFwAAgIkIXwAAACYifAEAAJiI8AUAAGAiwhcAAICJCF8AAAAm+v8A/d7ALbKnXgcAAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.barh(list(school.keys()), list(school.values()), color=\"maroon\") # barh statt bar\n",
|
||
"\n",
|
||
"plt.xlabel(\"Anzahl Kinder\") \n",
|
||
"plt.ylabel(\"Klassenstufen\") \n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "df9117c3-0ca8-4e0d-8779-9b8826044a3a",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-3adde3f53176bcb0",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Pie Chart\n",
|
||
"\n",
|
||
"Kommen wir als Nächstes zu einer beliebten und anschaulichen Darstellung von Daten: dem **Kuchendiagramm** (Pie Chart).\n",
|
||
"\n",
|
||
"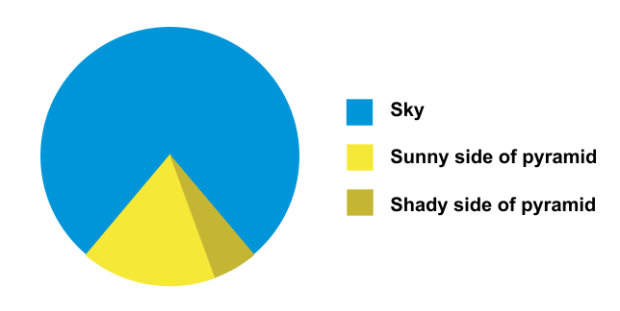\n",
|
||
"\n",
|
||
"Kuchendiagramme lassen sich in Matplotlib mit `plt.pie` erstellen. \n",
|
||
"\n",
|
||
"Wir nutzen dazu wieder das Beispiel aus dem vorherigen Kapitel. Für ein Pie Chart werden in erster Linie nur die **Werte** benötigt, z. B. `school.values` aus dem Datenset."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 52,
|
||
"id": "bb311d1b-978d-41f8-9648-874b4a862bc5",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-46cde6d166912ad0",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAGbCAYAAAAr/4yjAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAPJNJREFUeJzt3Xd4VFXCBvD3zmRm0ntCSAgBQm8iUUCKSE0ixYIgYKGJIH6L7ueK5WMXXV37ggq7IqiIFUVsrEpRQYr0JkgLXXpCCumZcr4/Qu4SkkDKTM7ce9/f8+QJTKa8U99bzpyrCCEEiIiIAJhkByAiIu/BUiAiIhVLgYiIVCwFIiJSsRSIiEjFUiAiIhVLgYiIVCwFIiJSsRSIiEil21J45plnoCiK7BiGdsstt+CWW25R/3/s2DEoioL3339fWiZ34mvMvd5//30oioJjx465/boVRcH//M//uPU6mzRpgrFjx7r1Or2Bpkqh7EWzdevWcqfn5OSgS5cu8PX1xbJlyySl05fvv/8ezzzzjOwYVEvFxcWYPXs2evbsibCwMFitVsTGxmLo0KH49NNP4XQ6ZUckL6WpUqjMxYsXMXDgQPz222/46quvkJKSIjuSLnz//fd49tln63QdK1aswIoVK9yUyPtMnz4dhYWFsmNUkJ6ejh49emDq1KkIDAzE9OnT8fbbb+NPf/oT8vPzMXr0aLzwwguyY5KX8pEdoC5yc3ORnJyMnTt34ssvv0RqaqrsSJqXn5+PgIAAt1yX1Wp1y/V4Kx8fH/j41P9bqKioCFarFSZT5ct09913H3bs2IElS5bgzjvvLPe3p556Clu3bsWBAwfqdBukX5p9xvPy8pCSkoLt27djyZIlGDRo0DUvs2DBAvTt2xfR0dGw2Wxo27Yt3nrrrQrn27p1K5KTkxEZGQk/Pz80bdoU48ePL3eeRYsWISkpCUFBQQgODkaHDh3wxhtvlDtPdnY2Hn30UcTHx8Nms6F58+Z4+eWX4XK51POUbWd/7bXXMG/ePCQmJsJms+HGG2/Eli1b1PO99tprUBQFx48fr5D3qaeegtVqRVZWlnrapk2bkJKSgpCQEPj7+6N3795Yv359ucuVbRPfu3cvRo8ejbCwMPTs2RNjx47Fv/71LwCl22LLfsq4XC68/vrraNeuHXx9fdGgQQNMmjSp3O0DFfcpVKaq84wdOxZNmjSp8eNUZvHixWjbti18fX3Rvn17fPXVVxWu82p++OEH9OrVCwEBAQgKCsKgQYPw+++/lztPZfsUyrZdf/3112jfvj1sNhvatWtX6WbNU6dOYfz48WjQoIF6vvfee6/ceVavXg1FUbBo0SJMnz4dcXFx8Pf3x8WLFyvNvWHDBixfvhwPPvhghUIoc8MNN+Cee+6p1m1Utd+ksu3/TZo0weDBg7Fu3Tp1c26zZs3wwQcfVLj877//jr59+8LPzw+NGjXC888/X+59UaY670WXy4U33ngDHTp0gK+vL6KiopCSklJhMzOAaz4vVb1Gqrv/qDrveW+nyTWF/Px8pKamYsuWLfjiiy8wePDgal3urbfeQrt27TB06FD4+Phg6dKlmDJlClwuFx5++GEAwPnz5zFw4EBERUXhySefRGhoKI4dO4Yvv/xSvZ6VK1di1KhR6NevH15++WUAwL59+7B+/Xo88sgjAICCggL07t0bp06dwqRJk9C4cWP8+uuveOqpp3DmzBm8/vrr5bJ98sknyM3NxaRJk6AoCl555RXceeedOHLkCCwWC0aMGIFp06bh888/x+OPP17usp9//jkGDhyIsLAwAMDPP/+M1NRUJCUlYcaMGTCZTGohrl27Fl26dCl3+eHDh6NFixZ44YUXIITA9ddfj9OnT2PlypX48MMPKzyOkyZNwvvvv49x48Zh6tSpOHr0KObMmYMdO3Zg/fr1sFgs1Xo+auNajxMAfPfdd7j77rvRoUMHvPjii8jKysKECRMQFxdXrdv48MMPMWbMGCQnJ+Pll19GQUEB3nrrLfTs2RM7duy4ZrGsW7cOX375JaZMmYKgoCC8+eabGDZsGE6cOIGIiAgAwLlz59CtWze1RKKiovDDDz9gwoQJuHjxIh599NFy1/ncc8/BarXiL3/5C4qLi6tcC1u6dCkA4N57763Wfa3NbVzNoUOHcNddd2HChAkYM2YM3nvvPYwdOxZJSUlo164dAODs2bPo06cPHA4HnnzySQQEBGDevHnw8/Mrd13VeS8CwIQJE/D+++8jNTUVDzzwABwOB9auXYuNGzfihhtuUM9XneelLmr6nvdaQkMWLFggAIiEhARhsVjE119/XeV5Z8yYIa68ewUFBRXOl5ycLJo1a6b+/6uvvhIAxJYtW6q87kceeUQEBwcLh8NR5Xmee+45ERAQIA4ePFju9CeffFKYzWZx4sQJIYQQR48eFQBERESEyMzMVM/3zTffCABi6dKl6mk33XSTSEpKKnd9mzdvFgDEBx98IIQQwuVyiRYtWojk5GThcrnK3femTZuKAQMGqKeVPUajRo2qkP/hhx+u8PgJIcTatWsFAPHxxx+XO33ZsmUVTu/du7fo3bu3+v+y+7pgwYIqz1NmzJgxIiEhocJlq/M4dejQQTRq1Ejk5uaqp61evVp97VxNbm6uCA0NFRMnTix3+tmzZ0VISEi50yt7jQEQVqtVHDp0SD1t165dAoCYPXu2etqECRNEw4YNRUZGRrnLjxw5UoSEhKiv1VWrVgkAolmzZpW+fq90xx13CAAiOzu73OmFhYUiPT1d/cnKylL/drXbqOw+CvHf9+LRo0fV0xISEgQAsWbNGvW08+fPC5vNJh577DH1tEcffVQAEJs2bSp3vpCQkHLXWZ334s8//ywAiKlTp1b42+Wv/+o+L1e+7q72OCQkJIgxY8ao/6/ue97baXLz0blz5+Dr64v4+PgaXe7yJZGcnBxkZGSgd+/eOHLkCHJycgAAoaGhAID//Oc/sNvtlV5PaGgo8vPzsXLlyipva/HixejVqxfCwsKQkZGh/vTv3x9OpxNr1qwpd/67775bXdIHgF69egEAjhw5Uu4827Ztw+HDh9XTPvvsM9hsNtx2220AgJ07dyItLQ2jR4/GhQsX1NvNz89Hv379sGbNmgqrspMnT67yflR2v0JCQjBgwIBy9yspKQmBgYFYtWpVta+rNq71OJ0+fRq7d+/G/fffj8DAQPV8vXv3RocOHa55/StXrkR2djZGjRpV7v6ZzWZ07dq1Wvevf//+SExMVP/fsWNHBAcHqxmFEFiyZAmGDBkCIUS520lOTkZOTg62b99e7jrHjBlTYUm6MmWblS6/7wAwd+5cREVFqT89e/ascNnq3sbVtG3bVn1OACAqKgqtWrUq9zr+/vvv0a1bt3JrrFFRUeU2aQHVey8uWbIEiqJgxowZFf525eaeaz0vdVXT97y30mQpvP3227BarUhJSbnmDrPLrV+/Hv3790dAQABCQ0MRFRWFp59+GgDUUujduzeGDRuGZ599FpGRkbjtttuwYMECFBcXq9czZcoUtGzZEqmpqWjUqBHGjx9fYdtkWloali1bVu6NGBUVhf79+wMoXTW+XOPGjcv9v+yD7/Lt9MOHD4fJZMJnn30GoPTDZfHixUhNTUVwcLB6u0DpG/zK237nnXdQXFys3tcyTZs2rfZjmJaWhpycHERHR1e4/ry8vAr3y92u9TiV7XNp3rx5hctWdtqVyh6/vn37Vrh/K1asqNb9uzJjWc6yjOnp6cjOzsa8efMq3Ma4ceMAVHx9VPc5CgoKAlC6z+1yw4YNw8qVK7Fy5Up07Nix0svW5HVQlWvdd6D0OWrRokWF87Vq1arc/6vzXjx8+DBiY2MRHh7ulmx1UdP3vLfS5D6Ftm3b4vvvv0e/fv0wYMAArF+//pprDYcPH0a/fv3QunVrzJw5E/Hx8bBarfj+++8xa9YsdelZURR88cUX2LhxI5YuXYrly5dj/Pjx+Oc//4mNGzciMDAQ0dHR2LlzJ5YvX44ffvgBP/zwAxYsWID7778fCxcuBFC682vAgAGYNm1apXlatmxZ7v9ms7nS84nLjpYaGxuLXr164fPPP8fTTz+NjRs34sSJE+p+jbLbBYBXX30VnTp1qvQ6r1yKrMnSocvlQnR0ND7++ONK/x4VFVXt6wJKH29RyRFhqxpHX53HqS7KHr8PP/wQMTExFf5endFG18pYdhv33nsvxowZU+l5r/zgru5z1Lp1awDAnj170KNHD/X0+Ph49T1StiR7pcpuo6qdq/Xx/FTnvVgT1clW0/t7uZq+572VJksBALp06YKvv/4agwYNwoABA7B27dqrfiAtXboUxcXF+Pbbb8stMVS1OaBbt27o1q0b/vGPf+CTTz7BPffcg0WLFuGBBx4AUDrccsiQIRgyZAhcLhemTJmCt99+G3/961/RvHlzJCYmIi8vT11KcJe7774bU6ZMwYEDB/DZZ5/B398fQ4YMUf9etnocHBxcp9uu6s2RmJiIH3/8ET169Kjzpgag9AOqstX3ykZZVUdCQgKA0h2eV6rstCuVPX7R0dFuf+7KREVFISgoCE6n0+23MXjwYLz00kv4+OOPy5VCbZWtiWVnZ6ubc4DaPz9A6XNUtkZ2uarW+q/2XkxMTMTy5cuRmZlZrbWFawkLC0N2dnaF06tzfz31nq9vmtx8VKZfv3749NNPcejQIaSkpFQ5TA/471LC5UsFOTk5WLBgQbnzZWVlVViqKVviLlttvXDhQrm/m0wmdcmu7DwjRoxQhwdeKTs7Gw6Hozp3sYJhw4bBbDbj008/xeLFizF48OBy3ytISkpCYmIiXnvttQqbEIDSTRfVUXadV75BRowYAafTieeee67CZRwOR6VvqKtJTEzE/v37y+XatWtXheGz1RUbG4v27dvjgw8+KHf/f/nlF+zevfual09OTkZwcDBeeOGFSrdjV/fxuxqz2Yxhw4ZhyZIl2LNnj1tvo0ePHhgwYADmzZuHb775ptLz1GSpvawkL98enp+fr64R18att96KjRs3YvPmzepp6enpFdY+q/NeHDZsGIQQlX7RsjZrJ4mJicjJycFvv/2mnnbmzBl89dVX17ysp97z9U2zawpl7rjjDsyfPx/jx4/H0KFDsWzZMvj6+lY438CBA9Wl+0mTJiEvLw/z589HdHQ0zpw5o55v4cKF+Pe//4077rgDiYmJyM3Nxfz58xEcHIxbb70VAPDAAw8gMzMTffv2RaNGjXD8+HHMnj0bnTp1Qps2bQAAjz/+OL799lsMHjxYHZKXn5+P3bt344svvsCxY8cQGRlZ4/sbHR2NPn36YObMmcjNzcXdd99d7u8mkwnvvPMOUlNT0a5dO4wbNw5xcXE4deoUVq1aheDgYHXY4tUkJSUBAKZOnYrk5GSYzWaMHDkSvXv3xqRJk/Diiy9i586dGDhwICwWC9LS0rB48WK88cYbuOuuu6p9f8aPH4+ZM2ciOTkZEyZMwPnz5zF37ly0a9fuqiV/NS+88AJuu+029OjRA+PGjUNWVhbmzJmD9u3bV1qUlwsODsZbb72F++67D507d8bIkSMRFRWFEydO4LvvvkOPHj0wZ86cWuW63EsvvYRVq1aha9eumDhxItq2bYvMzExs374dP/74IzIzM2t93R999BFSUlJw++23IzU1Ff3790dYWBjOnj2LH3/8EWvWrKn2Fz0HDhyIxo0bY8KECXj88cdhNpvx3nvvqY9JbUybNg0ffvghUlJS8Mgjj6hDUhMSEsp9GFfnvdinTx/cd999ePPNN5GWloaUlBS4XC6sXbsWffr0qfF8RyNHjsQTTzyBO+64A1OnTlWHI7ds2bLCzv8reeo9X+8kjHiqtbJhcJUNUXvttdcEADF48GBht9srHUL27bffio4dOwpfX1/RpEkT8fLLL4v33nuv3DC47du3i1GjRonGjRsLm80moqOjxeDBg8XWrVvV6/niiy/EwIEDRXR0tLBaraJx48Zi0qRJ4syZM+VuLzc3Vzz11FOiefPmwmq1isjISNG9e3fx2muviZKSEiHEf4davvrqqxXuEwAxY8aMCqfPnz9fABBBQUGisLCw0sdqx44d4s477xQRERHCZrOJhIQEMWLECPHTTz+p5yl7jNLT0ytc3uFwiD/96U8iKipKKIpS4bGcN2+eSEpKEn5+fiIoKEh06NBBTJs2TZw+fVo9T3WGpAohxEcffSSaNWsmrFar6NSpk1i+fHmVQ1Kr+zgtWrRItG7dWthsNtG+fXvx7bffimHDhonWrVtX+nhdadWqVSI5OVmEhIQIX19fkZiYKMaOHVvudVDVkNSHH364wvVdOXxRCCHOnTsnHn74YREfHy8sFouIiYkR/fr1E/PmzSuXA4BYvHhxtXKXKSwsFK+//rq46aabRHBwsPDx8RExMTFi8ODB4uOPPy43nPpat7Ft2zbRtWtX9bU+c+bMKoekDho0qMLlKxt2/Ntvv4nevXsLX19fERcXJ5577jnx7rvv1vi9KETpa/XVV18VrVu3FlarVURFRYnU1FSxbds29Tw1eV5WrFgh2rdvL6xWq2jVqpX46KOPqjUkVYjqvee9nSKEm/bQEXm5Tp06ISoq6qpDiYmMTtP7FIgqY7fbK2y/Xb16NXbt2nXNaTeIjI5rCqQ7x44dQ//+/XHvvfciNjYW+/fvx9y5cxESEoI9e/a4ZUoDIr3S/I5moiuFhYUhKSkJ77zzDtLT0xEQEIBBgwbhpZdeYiEQXQPXFIiISMV9CkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqlgIREalYCkREpGIpEBGRiqVAREQqH9kBiNzN4XThfG4xzl0sQnaBHQUlTuSXOFBY4kRBiRMFJY5Lv50osjuhADCblIo/igKzWYGfxYxQPwtC/a0I8bcg1M+CMH8rQv0tCPa1wGRSZN9lIrdhKZDmZBeU4ND5PBxOz8Pp7CKczy3CuYulJXDuYhEy80vgEvWTxaQAIX4WxIX5IT7MH/Hh/ogP8yv9He6PRmF+sPmY6ycMkRsoQoh6evsQ1cyZnEIcOp9X7udweh4y8kpkR6s2RQGig2xIjApEq5ggtIkJRquYILSKCYKvhWVB3oelQF6hoMSBXX/kYPuJLOw4kY2df2QjI69YdiyP8TEpaB4diPZxIegQF4KOjUp/+5i5m4/kYimQFH9kFmDT0UzsuFQCB87lwllf23y8VIDVjM4JYejWLALdmkXgukYsCap/LAWqF4VFxfjlUBbWpqVj3aEMHL9QIDuS1/O3mpF0WUlcHx/KndrkcSwF8pyMNODgMuDgctizTqLFuX/ITqRpEQFW9G0djYHtYtCrRST3SZBHsBTIvY5vAPZ9CxxcDmQeLvencf5zsCozXFIwffG3mtGrRSQGto1BvzbRCPW3yo5EOsFSoLrL/gPY9WnpT+aRKs+2vNFUTDrUrR6DGYOPSUGXpuEYel0sBl8Xi0AbR5pT7bEUqHZKCoC93wA7PwaOrQNw7ZdRZkxPdD42xfPZDMzPYkZK+xjcldQI3RMjoCjcB0E1w1Kg6hMCOL4e2PlpaSGU5Nbs4j6+6FQ8Dzl2LsnWh7hQPwzrHIe7kuLROMJfdhzSCJYCXVvW8f9uHso6Vqer+mf0PzD7RFP35KJqURTgxibhuP+mBKS2bwgzRzDRVbAUqGqndwLrZpXuOBYut1zl3vhRuDVtiFuui2ouLtQPY7s3wcgu8QjytciOQ16IpUAVHV1TWgaHf3b7VZeENEVLDk2VLtDmg+E3NML4Hk0RH85NS/RfLAUqJQSw/7vSMji11aM3dbfvXGzKDvbobVD1mE0KBrZtgAd6NUNSQpjsOOQFWApG53QAuz8H1r8BpO+vl5v8ttH/YuqhG+rltqj6erWIxGMDW6FTfKjsKCQRS8GoSgqA7R8AG+YAOX/U602nx/bFjUceqNfbpOrr3yYafx7QEu1iQ2RHIQlYCkbjcgE7PgB+fh7IT5cSQVgD0D7/beQ7Odmbt1IUILV9DP53QEs0jw6SHYfqEUvBSI6tA5Y9CZzdLTsJno94Ge+cipcdg67BpABDr4vFYwNbcYe0QbAUjCDrOLBieunQUi+xM/5+3J6WIjsGVZPNx4QHb26GKbc0h5+VE/HpGUtBz0rygbX/BDb8C3AUyU5TTlF4K7Q+PUN2DKqhuFA/PH1rGwzq2FB2FPIQloIeCQHsWgT89CyQe0Z2mioNsczH7twA2TGoFronRuCZoe3QsgH3N+gNS0Fv/tgCLHsCOLVNdpJrWhw7DY8f6SQ7BtWSj0nBfTcl4M8DWiKY347WDZaCXhTnASv+D9i2ENWZsdQbnIlLxk2Hx8iOQXUUFWTDC3d0wIC2DWRHITdgKejBiY3AV5PqPFldfRO2ELTM/TfsLk7Qpgd3Xh+HGUPaIcSfaw1axoHiWuYoAVbOABakaq4QAEApzsHwBt67z4Nq5ssdpzBg1i/4ad852VGoDlgKWnXud2B+X2D9626bwVSG2wP3yY5AbnQ+txgTFm7FY5/vQk6hXXYcqgWWgta4XMC614F5twDn5H8Jra7aF26RHYE8YMn2k0ietQarDpyXHYVqiPsUtCTrGPDVZODEBtlJ3EZAQX/TOzhc4Cc7CnnIhJ5N8WRqa1jMXAbVAj5LWrFtIfBWD10VAgAoEBjb4LDsGORB7647irve+hV/ZBbIjkLVwFLwdvZC4IsJwNKpQEme7DQe0dv8m+wI5GG7Tubg1jfXYvnvZ2VHoWvg5iNvlnMKWDQaOLNTdhKPcvlFIjH7DQjBoalGMOnmZpiW0prHivZSXFPwVn9sBub30X0hAICpMAO3R8uZxpvq39trjmD0/I04n+td83FRKZaCN9rxMfD+YCDPOOO9hwVzaKqRbDqaidvmrMfe0xdlR6ErsBS8icsJLHsK+GYK4CyWnaZeXVfs/XM1kXudySnC8Lm/4uf9xln40QKWgrcozAY+vgvY+G/ZSaQITN+BOF9jFSEB+SVOTPxgGxasPyo7Cl3CUvAG6QdLv518+GfZSaRRhBNjY47JjkESOF0Czy7dixnf7IHTxXEvsrEUZEv7EXinH5DJsfr9fDg01cgWbjiOCQu3IK/YITuKobEUZPr9a+DTkUAxd7YBQEL2RtkRSLLVB9Jx11u/4vxFjkyShaUgy67PgC/GAy5OGlbGnHcGyZEXZMcgyfafzcXwtzfgZBa/AS0DS0GG7R8AX08GhFN2Eq8zIuyA7AjkBY5fKMDdb2/EsYx82VEMh6VQ3zbPB76dqunprj0pyc6hqVTqVHYhhr+9AQfP5cqOYigshfr062zg+79AK4fLlCEkfRsirNykRqXSc4sxct5G7DmVIzuKYbAU6ssvrwIrpstO4fUUZwnGxJyQHYO8SGZ+CUbN34htx7NkRzEElkJ9+Ok5YNXzslNoRrJtj+wI5GVyixy4/91N2HosU3YU3WMpeNry/wPWviY7haYk5ujrmBHkHvklTox7fwt+P81NSZ7EUvCklTOADXNkp9Acn4sn0Cs8W3YM8kK5RQ6MeW8zjnJUksewFDxl83xg/euyU2jW6PCDsiOQl8rIK8G972zC2Rx+wc0TWAqecOAH4IcnZKfQtC7OHbIjkBc7lV2Ie9/dhKz8EtlRdIel4G4nt5V+U5lfTKuT8IwtCPLhHDhUtUPn8zB2wWbOleRmLAV3yjwKfHo3YOfX8+tKsRfg3oYnZccgL7frZA4mLtyKEge/DOouLAV3KcgsPR5CPg8r6S63+v4uOwJpwIYjFzD9692yY+gGS8Ed7EXAp6OAC4dkJ9GVVnmbZUcgjfh860m8s/aI7Bi6wFKoK5cL+OpB4A9O++xu1qw0dA7hvDdUPS/+sB+rDpyXHUPzWAp1tWI6sPcb2Sl0677INNkRSCOcLoGpn+zAofNckKgLlkJdbHkX2Pgv2Sl0rbvYKTsCaUhusQMPLNyK7AIOVa0tlkJtndoOLHtSdgrdi76wCX5mDu+l6jt2oQAPfbQdDidHJNUGS6E2CrOAxWMAJ5dGPE0pzsWIBmdkxyCN2XDkAl78Yb/sGJrEUqgpIYCvHgKyOb1zfRkasFd2BNKgd9cdxU/7zsmOoTkshZpa/wZw8AfZKQylbcEW2RFIo/6yeBfnSKohlkJNnNgE/Pyc7BSG43thL1oH8lviVHNZBXZMXbQDThePdlhdLIXqKsoBvnwAcHGelfqmQGBs9GHZMUijNh/NxJs/cWhzdbEUqus/f+Z+BIl6KTtlRyANm7PqEDYeuSA7hiawFKpj5yfAniWyUxhawwsbYVY4xJBqx+kSeHTRTmRyqu1rYilcy4XDwPePy05heKaiLAxrwCkMqPbOXizCX7/m8b+vhaVwNUIAX00GSvJkJyEAdwTtkx2BNO673WewbM9Z2TG8GkvharYtAE5ypk5v0bGIQ1Op7v76zR7kFNplx/BaLIWq5KUDPz4jOwVdxj/jNzT245hzqpv03GI8/x9+IbIqLIWqLH+6dBgqeQ1FuDAu5qjsGKQDi7edxJqDPCBWZVgKlTmyGtj9uewUVIk+5l2yI5BOPPXlbuTz+M4VsBSu5CgGvntMdgqqQnzWRigKv51KdXcquxCvLj8gO4bXYSlcad0sHlbTi5nzz2NQZIbsGKQTCzccw28ns2XH8CoshctdOAysnSk7BV3D8FBOiUzuIQTwHHc6l8NSuNx3/ws4i2WnoGu4vmSb7AikI1uOZWHprtOyY3gNlkKZ3xaX7mAmrxeUvgMxNk5XQO7z0g/7UWTnEf4AlkKpooulQ1BJExSXHffHHJcdg3TkVHYh3ll7RHYMr8BSAICN/wbyOa+Olgyw7pYdgXTm36sP4/xFfjmSpVCYBWz4t+wUVENNszfIjkA6U1DixMvLOESVpfDrHKCY31zWGp/cU+gbkSk7BunMlztOYvdJY38eGLsUCjKBTXNlp6BaGhl2UHYE0hkhgH+uNPbagrFLYf3rnBZbw250cGgqud/qA+nYfiJLdgxpjFsKeeeBzfNlp6A6CE3fijAL564h95u5wrhrocYthXWzAHuB7BRUB4qzGPc15HGzyf3WHcrAlmPG3GdlzFK4eAbY+p7sFOQGKbbfZUcgnXrzpzTZEaQwZims/Sfg4HhkPWh+caPsCKRTa9MysOuPbNkx6p3xSiHnJLB9oewU5CbWnKPoGnpRdgzSqdk/G2/GZOOVwrpZgJPz5ujJvRHG3SlInvXT/nNIO5crO0a9MlYpFOcCuxbJTkFu1s21Q3YE0ikhSo+5YCTGKoVdi/i9BB2KzNiMALNLdgzSqS+3n8LFIrvsGPXGWKXAEUe6pNjzMTrmpOwYpFMFJU58vuUP2THqjXFK4fivwHkeYUmvBvtzaCp5zocbj8PlMsaxwY1TClvelZ2APKhV/mbZEUjHjl8owOqDxphe3xilkJcO7PtWdgryIN/MA+gQlC87BunY+78a48BOxiiFHR9yGKoBjIky3phyqj9r09JxOF3/A1X0XwouF7BtgewUVA96KByaSp4jBLBos/7n2tJ/KRz6EcjW/xNJQEzGRthMHJpKnvPNztO63+Gs/1LYyh3MRqEUX8TwBmdkxyAdO59bjPWHM2TH8Ch9l0L2H0DaCtkpqB7dFrhPdgTSua92nJIdwaP0XQp7vwEENycYSbvCLbIjkM4t33MWhSVO2TE8Rt+lsG+p7ARUz/wy9iDRv1B2DNKx/BInVuw9KzuGx+i3FPLOAyf5hSajUSAwtsFh2TFI5/S8CUm/pbD/O246MqhbzL/JjkA6ty4tAxl5xbJjeIR+S4Gbjgwr7sIGmBUuEJDnOFwCy/bocxOSPkuhKAc4ukZ2CpLEVHgBt0Wny45BOvfzfn3OhaTPUji4AnAZZ/5zqmhY8H7ZEUjnfj2cgSK7/kYh6bMUOPmd4V1XvFV2BNK5IrsL6w/p74ts+isFexFw6CfZKUiygPSdiPPV545A8h4/6XATkv5K4fDPgJ1TKBudIpwYG3NUdgzSuVUsBQ3Y/x/ZCchL9PPZLTsC6dyZnCLsPX1Rdgy30l8pcK4juiQhe6PsCGQAP+8/JzuCW+mrFDIOAfkcikilzHlnkBqlvx2B5F1+Oaivzxx9lcIfm2QnIC8zPPSA7Aikc7tO5qDYoZ+hqTorBW4uoPKSSrbJjkA6V+Jw4beTObJjuI2+SuEE1xSovOCM7Yiy8ouM5FlbjmXKjuA2+imFwiwg46DsFORlFGcJ7o85LjsG6dzWY1myI7iNfkrhj80A9H3sVKqdgbY9siOQzm07ngUh9PH5o59SOMH9CVS5xBy+NsizcgrtOHguT3YMt9BPKfzBA+pQ5XwunkCv8GzZMUjn9LJfQR+l4LQDpzjKhKo2Opz7m8izth3Xx34FfZTCmd8AB4/LS1Xr4twuOwLp3L4z+pjuQh+lwC+t0TWEp29BkI9DdgzSsSPp+XA4tX/EP32UwpldshOQl1Mchbgv5qTsGKRjJU4XjmRof4ZmfZRC5mHZCUgDUv1+lx2BdG7/2VzZEepMH6VwgaVA19Yql5sZybMOnNX+fgXtl0JhFlCoj6Fg5FnW7EPoHKL9JTnyXgfOav+7CtovhQtHZCcgDbkvMk12BNKxA+e4piAf9ydQDXQXO2VHIB07mVWI/GJtj3LTQSlwTYGqLzpjI/zM+pn7nryLEMDxCwWyY9SJ9kuBO5mpBpSSPIxscFp2DNKx09na/iKt9kuBm4+ohoYE7JUdgXTsdA5LQS6uKVANtSnYIjsC6dgprilIVJAJFGXLTkEa43dhL9oEanu7L3mvM9lFsiPUibZLgWsJVEtjovnaIc/gPgWZLp6SnYA0qpeyU3YE0imWgkzcdES11PDCRlhM+jh8InmXc7nFcLq0+9rSeCnkyE5AGmUqysKwBmdlxyAdcroE0nOLZceoNY2Xgva/Uk7y3B64T3YE0qncIrvsCLWm8VLgmgLVXodCDk0lz7hYpN2pLlgKZFj+F3ajiZ+2hw+Sd+KagizF3HxEtacIF8bGHJUdg3Qol2sKknBNgeroFjMP5Urux1KQhaVAdRSftRGKot3hg+Sd8oq5+UgOjj6iOjLnn8fgqAzZMUhnuKYgC9cUyA2Gh+yXHYF0hqUgg8sJlGj/eKgkX6firbIjkM4UO7R7ICftloK9AAC3BVPdBWXsQIytRHYM0hGXS3aC2tNuKUCRHYB0QnE5MDbmmOwYpCNOod0FVu2WgqLd6OR9+lt3y45AOuLScCn4yA5QaywFTRNQYDdb4PCxwm7ygd3HCofZCrvZDLvZArviA4fZB3azD+wmM+wmMxwmH9hNJjhMZtgVU+m/FRPsigK7YoJDUWBXlNLfAOwK4IACuyJgh4ADuPRbwC5csMMFhyj996BTFnz/+3zZDwvphDWsF4BOsmPUCktBBxyKufTD1Wy57IPWctmH6qUPWMUMu7nsw9UMh8lUelrZh6vJdOlD1QS7Athx6QNWQelvIS590JZ+uNrhuvQBK+C49CFrFy44hBP2Sz8O4YLd5Sg9zeWA3WWHw+WEQ1Q1OkMAKLn0cwXXpR8PePIXASXtoGeunAzHv10b2RFqTbulYDK7/SoFFDgufbCW/ljh8LGUfrCWW3o1l37QXlqCLf2ALV16Lf2tXPbhWn7ptfT3lR+u/116VZdihQsOuGB3lX24XvqgvewD1uFywCEccImqPikdl34q3FHAeemH0KewCcy7WQjkRmbtLrRquhRe7jy4dClVKftwxWWbBv679OoQrvJLrsIBu8tZ7sPVfukDtnJyll6pfozaHSw7AumMYmIpSPF5zn6UuDiUkGqvsTMUYWv3cHAzuZcHtmTUF+3WGQCbj012BNK4yceaQZRwwYLcy+TvLztCrWm7FMwsBao9qzCjxaojsmOQDpmDg2RHqDWWAhnWhIy2EOmcDI/czxSk3f1Umi4FX7Ov7AikYb03cO4s8gxzUKDsCLWm6VIIsYXIjkAa1b+gKUy/p8mOQTrFNQVJIv0iZUcgjRq5W7vbfMn7cZ+CJCwFqo0mjlAEr+VcR+Q5XFOQJMo/SnYE0qDJR5sBdu0eLpG8H9cUJInwjZAdgTTGJsxovvqQ7Bikc1xTkISbj6imJqa3gysjU3YM0jGTvz/MgQGyY9QaS4EMpeevF2VHIJ2zxMXKjlAnLAUyjJT8RJj2cdMReZYlNk52hDrRdCmE+4bDxOMqUDWN2KXd+WhIOyxxLAVpzCYzQm2hsmOQBiQ6whG4nsNQyfNYCpLFBMTIjkAaMOlIE8BR1fEyiNyHpSBZYkii7Ajk5XyFD5qu4pQWVD+4o1myZqHNZEcgLzfpXDuIzCzZMcgguKYgWfPQ5rIjkJfr/isLgeqH4u8Pn/Bw2THqRPOlkBjKzUdUtcF5iVAO8EA6VD9sTZvKjlBnmi+FuMA4+Pn4yY5BXmrYLr42qP7Y2rSWHaHONF8KJsWEJsFNZMcgL9TCEYGAX/fIjkEG4tu6jewIdab5UgC4X4EqN+lQAoehUr3y5ZqCd+AIJLpSoLAiYfVB2THISBQFtlYsBa/ANQW60oNn20BkZcuOQQZiiY/X9OyoZVgKpEvd1nN6bKpfvq21v5YA6KQUGgU14gF3SHVbbnMg7ajsGGQwetifAOikFACgc4POsiOQl7hjp012BDIgWxvtjzwCdFQKSQ2SZEcgL9DaHgn/DRyGSvVMUeB33XWyU7iFbkrhhgY3yI5AXuDBtMaA0yk7BhmMrWVL+ISFyY7hFrophRZhLRBkDZIdgyQKctkQv3q/7BhkQP5dusiO4Da6KQWTYsL10dfLjkESTT7bBiKHx2Cm+hfQlaXglbhfwdhuXJcuOwIZkaLA/wb9bL5mKZAu3JnbEjh8XHYMMiBb69Ywh4bKjuE2uiqFthFtOWOqQd223Ud2BDKogC43yo7gVroqBYvJgo5RHWXHoHrW3t4Afhs5DJXk8O/aVXYEt9JVKQBAr7hesiNQPZt4IBZwuWTHICMymXS1PwHQYSn0bdxXdgSqRyEuX8RyGCpJ4t+5M8zBwbJjuJXuSiE+KB4tw1rKjkH1ZPKZ1hC5ubJjkEEFDRwgO4Lb6a4UAKBf436yI1A9uWHtedkRyMCC+veXHcHtWAqkWSMutoY4ekJ2DDIo33btYImNlR3D7XRZCq3CW6FRYCPZMcjDhmxTZEcgAwsaoL+1BECnpQBwbUHvOpXEwLb5d9kxyMCCBuhvfwKg51JIYCno2fgDDTkMlaSxNmsGW2Ki7BgeodtS6BTVCZF+kbJjkAeEufzQ8Jd9smOQgelxB3MZ3ZaCoijoE99HdgzygIdOtYbIzZMdgwwsOCVZdgSP0W0pAMDgZoNlRyA3UwRw/dozsmOQgdnatIFv27ayY3iMrkuhc4POSAzR53Y/oxqV0wbi+EnZMcjAQocNkx3Bo3RdCgAwrKW+n0CjSd0mZEcgA1NsNoQM0fcWCN2XwtDEobCZbbJjkBsklTSEbQuHoZI8QQMGwBwSIjuGR+m+FEJsIeifoN+RAkYybn8MILimQPKE3qX/LQ+6LwUAGNZC/0+k3kW6AtBg9V7ZMcjALPHxujt2QmUMUQo3xtyIJsFNZMegOnjoZEuI/HzZMcjAQofdCUXR/9QqhigFALir5V2yI1AtKQLouOaU7BhkZGYzQu64U3aKemGYUhiaOBRWk1V2DKqFe7PbQPxxWnYMMrCgAQNgaRAtO0a9MEwphPmGcT4kjUrZyjmOSK6ICRNkR6g3hikFABjXbpzsCFRDXYrjYNnGHcwkj3/XrvDr0F52jHpjqFJoE9EGveJ6yY5BNTB2XxSHoZJUEQ8YZy0BMFgpAMCk6ybJjkDVFO0MRNRqflmN5LG1bo3AXsZakDRcKVwXdR26xuh/rLEePHSyBURhoewYZGARE8bLjlDvDFcKADCx40TZEegazFDQ/hdOfEfyWGJjEZyaKjtGvTNkKXRt2BWdojrJjkFXcV9mW4hTnCKb5AkfOwaKj4/sGPXOkKUAcG3B2w3cYpcdgQzMHBGB0LuM+YVXw5bCzY1uRpvwNrJjUCW6F8XDZzuHoZI8kZMehMnfX3YMKQxbCgDXFrzVfXvDZUcgA/OJbYjQkSNlx5DG0KXQv3F/ri14mRhnICLXcBgqyRP18P/AZDXulDiGLgVFUfBElydkx6DLPHSiJURhkewYZFDWxESE3H6b7BhSGboUACCpQRIGJgyUHYMA+AgT2v5yXHYMMrDovzwGxWyWHUMqw5cCADx2w2M8ZKcXGJPVFuLMOdkxyKD8u3RBUJ8+smNIx1IAEBsYi/vb3i87huH138jNRiSJoiB62jTZKbwCS+GSBzo8gGg/Y8yX7o16FTWGedd+2THIoEKGDoVf+3ayY3gFlsIl/hZ/PJL0iOwYhnXvnjDZEcigzCEhiH6CawllWAqXGdJsCDpEdpAdw3DinMEIX8thqCRH1F8eg084vxtThqVwGUVRMO1GLjHUt4eON4co4v4Eqn9+SUmGnc6iKiyFK3SK7oShiUNlxzAMqzCj1epjsmOQEVksaPjsM1AURXYSr8JSqMS0G6chwjdCdgxDGHuhDcS587JjkAFFjBsHW/PmsmN4HZZCJUJsIZjebbrsGIbQZ2OB7AhkQJb4eEROeUh2DK/EUqhC/4T+GJAwQHYMXetT2ATm3QdlxyADivnbX2Hy9ZUdwyuxFK7i/7r+H8JsHCrpKaN2B8uOQAYUcvvthjvuck2wFK4iwi+Cm5E8pLEzFGFr98iOQQZjadwYDabzPX01LIVrGNhkIAY3Gyw7hu5MPtoMoqREdgwyEh8fxL3yMsyBAbKTeDWWQjU83fVpxATEyI6hG1ZhRovVR2THIIOJfGgy/Dp1kh3D67EUqiHIGoTnezwPBRzP7A4TMtpCpGfIjkEG4te5MyInT5YdQxNYCtXUtWFXjGs/TnYMXei9IU92BDIQU2AgYl95xfDHSagulkINTL1+KrrGdJUdQ9P6FzSF6fc02THIQGL+9ldYG8XJjqEZLIUaMJvMeKX3K9y/UAcjfwuSHYEMJHjoEIQM5bQ1NcFSqKFw33DM7D0TVpNxD+xdW00coQhet1t2DDIIW9s2aPj3v8uOoTkshVroENUBT3R5QnYMzZl8tBlgt8uOQQZgDg9H/Jw5/NZyLbAUamlEqxG4vfntsmNohk2Y0Xz1IdkxyAh8fBD3+ixYYmNlJ9EklkIdTO82HW3C28iOoQkT09vBlZEpOwYZQIOnnkRAly6yY2gWS6EObGYbZvWZhRBbiOwoXq/XrxdlRyADCLlrGMLvuUd2DE1jKdRRXGAcXrn5FfgoPrKjeK3U/EQo+7jpiDzLr1MnNPzb32TH0DyWght0j+2OZ3s8y288V2H4Ln/ZEUjnfGJiEPfmG1CsHBVYVywFNxmaOBR/Tvqz7BheJ9ERjsD1HIZKnmMOCUHjd+bDEh0tO4ousBTcaFz7cRjTdozsGF5l0pEmgMMhOwbplOLvj/i35/Kwmm7EUnCzx254jFNtX+IrfNB0Fae0IA+xWNDojdc586mbsRTcTFEU/L3H39EjrofsKNJNOt8OIjNLdgzSI0VB7Asv8AhqHsBS8ACLyYKZvWeiQ2QH2VGk6r6ehUCe0eCppxAyhGvknsBS8BB/iz/+1e9faBLcRHYUKQbnJUI5wAPpkPtFTJ6E8Pvvkx1Dt1gKHhTmG4Z5A+YhLtB40/YO2+UnOwLpUNg99yD60Udlx9A1loKHNQxsiIUpCw21xtDCEYGAX/fIjkE6Ez5uHGL+Ol12DN1jKdSDBgEN8H7K+2gZ1lJ2lHox+VACh6GSW0U8NBkNnpgmO4YhsBTqSYRfBN5Lfg/tI9rLjuJRgcKKxqsPyo5BOhL16KOIfuQR2TEMg6VQj0JsIZg/cD46R3eWHcVjHjzbBiIrW3YM0onoJ59A5ORJsmMYCkuhngVaAzF3wFzc1PAm2VE8ott6To9NbqAoiJnxN0SMHSs7ieGwFCTw8/HDnH5zcEv8LbKjuNVtuc2BtKOyY5DWmc1o+PzzCBs1SnYSQ2IpSGI1WzHrllm4temtsqO4zR07bbIjkMaZAgMRP3cuQofdKTuKYbEUJPIx+eDlm1/GlE5TND/tdlt7FPw3cBgq1Z4lNhYJn3yMwF49ZUcxNJaCF3jouofwz1v+CT8f7X7ha2JaI8DplB2DNMq3Y0c0+fwz+LY0xrBtb8ZS8BIDEgZgYcpCxATEyI5SY0EuGxqtPiA7BmlUUHIyEj5YCJ/ISNlRCCwFr9Imog0+HfQpOkZ1lB2lRiafbQORw2MwU81FTJyIuNdnweTrKzsKXcJS8DKRfpFYkLwAQ5oNkR2l2m5cly47AmmMYrWi4T/+gejH/heKou39aXrDUvBCVrMVL/R6AY92fhQmxbufomG5rYDDx2XHIA2xJDRGk88WcYSRl/LuTxyDm9BhAmb3nY0wW5jsKFUaus0sOwJpSFBqCpou+RK+bdrIjkJVYCl4uZsb3Ywvb/sS3WO7y45SQXt7A/ht4jBUujbFakXMjL+h0axZMAcGyI5DV8FS0IBIv0jM7T8Xj9/wOCwmi+w4qokHYgGXS3YM8nKWxo3RZNGn/IayRrAUNEJRFNzf7n58MugTNAtpJjsOQly+iF29X3YM8nJBKSlo+uUS+LZtKzsKVRNLQWNah7fGZ4M/w4iWI6TmmHymNURurtQM5L1MgYFo+PxzaPT6LJgDA2XHoRpQhBBCdgiqnZ9P/Ixnfn0GWcVZ9X7bixfFQhw9Ue+3S94voHt3NPzH87A0bCg7CtUC1xQ0rG/jvlgydEm9z7Y6IqcVC4EqMAUEIOaZGWj83rssBA3jmoJOrDqxCi9ufhFn8s94/LY+XNUGto27PX47pB2BvXsj5pkZLAMdYCnoSKGjEHN3zcUHez+Aw+WZYyR3KonB07NOc9QRAQDM4eFo8PTTCBk8SHYUchOWgg4dyjqE5zc9j23ntrn9ut/cfT1i/rPF7ddLGmM2I+zuEYj805/gE+a9X66kmmMp6Ng3h77BzG0zkVnknkNkhrn8MO/fAiI3zy3XR9oU0L07Gjz1JGwtWsiOQh7AUtC5nOIcvL79dSw5uAQCdXuqn/7jenT6iGsJRmVNSED0E08gqG8f2VHIg1gKBnEg8wDm7JyD1X+srtXlFQF8/mkMxPGTbs1F3s8UFITIKVMQfu89UCze84168gyWgsHsTt+N2TtmY8OZDTW63OjsNrj9LY44MhSLBaHD7kTU1KnwCQ+XnYbqCUvBoLac3YLZO2Zjx/kd1Tr/hz+1hm0zJ78zAsViQcgddyDiwQdhbRQnOw7VM5aCwa07tQ6zd8zG3gt7qzxPUklDPDHzJMCXiq4pVitC7xqGiIkT+X0DA2MpEADgp+M/Yc7OOTiUfajC3+b8dj2iv+MOZr1SbDaEDh+OiIkPwNKggew4JBlLgVRCCKw/vR4f/P6Bus8h0hWAt+Y4IPLzJacjdzP5+5eWwQMT4BMVJTsOeQmWAlUqLSsNH+79ENetPom2H9ZspzR5N2uzZggbPRoht9/GGUypApYCXZUjMxPZi79A1meL4Djt+XmVyEPMZgT17YOw0aMRcNNNstOQF2MpULUIpxN5q1cj65NPkb9hA+c+0ghzRARCh9+FsLvv5s5jqhaWAtWY/dx5XPzuO+QsXYrifftkx6ErKBYLAm6+GSGDbkVQ//5QrFbZkUhDWApUJ8Vpacj5dilyvvsPNy/JZDLBv2sXhAwahKCBA2EODpadiDSKpUBuIYRA4datyPl2KXJXrIAzJ0d2JEPwu+46BA8ahODUFI4gIrdgKZDbCacThbt2IW/1L8hbswbF+/fLjqQbiq8v/G+8EYE9eyCwb19Y4+NlRyKdYSmQx9nPnUPeL6UFUfDrBrgKCmRH0hRrYiICe/ZAQM9e8O9yI0w2m+xIpGMsBapXoqQEBVu3In/TZhTu2IHCPXsgWBLlmCMj4X/99Qjo2ROBvXrCEhsrOxIZCEuBpBJOJ4oPHEDBjh0o3LkLhTt2wH7SONNzK76+8G3bFn4dO8Lvuo7w69gRljhOQkfysBTI6zgyMlC4cyeK9h9A8eFDKDl8BCXHjkGUlMiOViem4GBYmzaBrVki/Dp2gG/HjvBt1QqKj4/saEQqlgJpgnA6YT95EsWHj6DkyGEUHz6C4iOHYT99Gs4Lmd7zZTqLBdb4eFibNCktgKZNL/27KXwiImSnI7omlgJpnnA64bhwAY7z6XCkn4cjPf2ynwy4Ll6Eq6gIoqgIruLi//4uLKy49qEoUCyW0h+r9b8/FgtMfn4wh4bCHBZ26ScUPpGR8ImKgk90dOnviAgoZrOcB4LIDVgKZGjC5YIoLgZcLrUIiIyMpUBERCqT7ABEROQ9WApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGpWApERKRiKRARkYqlQEREKpYCERGp/h+6hC0wRfAp4QAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.pie(school.values()) # Pie Chart\n",
|
||
"\n",
|
||
"plt.title(\"Klassenverteilung einer Grundschule\")\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "76e19a82-7aa7-416d-beae-667b77497cf3",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-aec08dc408437049",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Styling\n",
|
||
"\n",
|
||
"Alle üblichen Parameter wie `title`, `color`, `xlabel`, `ylabel` usw. lassen sich auch bei einem Pie Chart setzen. \n",
|
||
"\n",
|
||
"Die **Beschriftung der einzelnen Stücke** funktioniert jedoch etwas anders. \n",
|
||
"\n",
|
||
"Dazu wird der Parameter `labels` mit den entsprechenden Kategorienamen versehen, sodass jedes Segment des Kuchendiagramms eindeutig gekennzeichnet ist."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 53,
|
||
"id": "09124a3e-1f76-4f32-8638-19e7efc234b0",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-c742155fd484b71b",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAGbCAYAAAAFuq0xAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAUJFJREFUeJzt3XdcE/f/B/DXJSSEDTJkKAg4EMWFtSr6RQRFKu5VRBFHtVVbbX+t1W+nWlv91lr9dlhHRb91Vuuo1kWrKA5wAW7EgThAkb0hyf3+oKQiqCEEPknu/Xw8eIjhcvdKIHnl7j53x/E8z4MQQgjRgIh1AEIIIfqLSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEoEwOeffw6O41jHELQ+ffqgT58+qv+npqaC4zisX7+eWSZtor8x7Vq/fj04jkNqaqrW581xHGbOnKnVebZo0QKRkZFanaeuMNgSqfojO3fuXLXb8/Ly0K1bN8hkMhw8eJBROsOyf/9+fP7556xjEA2VlZXhu+++Q69evWBjYwOpVApnZ2cMHjwYW7ZsgUKhYB2R6DCDLZHa5Ofno3///rh48SJ27dqFAQMGsI5kEPbv34/58+fXax6HDx/G4cOHtZRI93z88ccoKSlhHaOGzMxM+Pn54Z133oG5uTk+/vhjrFq1Cm+//TaKioowduxYfPnll6xjEh1mxDpAYykoKEBwcDASExOxc+dOhISEsI6k94qKimBmZqaVeUmlUq3MR1cZGRnByKjxX26lpaWQSqUQiWr/vDh+/HgkJCTgt99+w/Dhw6v9bN68eTh37hySk5PrtQxi2ATxWy8sLMSAAQNw4cIF/Pbbbxg4cOBL7xMVFYW+ffvCwcEBxsbG8Pb2xsqVK2tMd+7cOQQHB8POzg4mJiZwd3fHpEmTqk2zdetW+Pr6wsLCApaWlvDx8cGKFSuqTZObm4vZs2ejefPmMDY2RsuWLbFkyRIolUrVNFX7CZYuXYrVq1fD09MTxsbGeOWVV3D27FnVdEuXLgXHcbh7926NvPPmzYNUKkVOTo7qtvj4eAwYMABWVlYwNTWFv78/Tp48We1+Vdv0r169irFjx8LGxga9evVCZGQkfvjhBwCV25KrvqoolUosX74c7dq1g0wmQ9OmTTFt2rRqywdq7hOpzfOmiYyMRIsWLer8PFXZvn07vL29IZPJ0L59e+zatavGPF/kwIED6N27N8zMzGBhYYGBAwfiypUr1aapbZ9I1bb33bt3o3379jA2Nka7du1q3cz64MEDTJo0CU2bNlVNt27dumrTxMTEgOM4bN26FR9//DFcXFxgamqK/Pz8WnOfPn0ahw4dwtSpU2sUSJWuXbsiPDxcrWU8b79PbfsvWrRogdDQUJw4cUK1ednDwwP/+9//atz/ypUr6Nu3L0xMTNCsWTN88cUX1V4XVdR5LSqVSqxYsQI+Pj6QyWSwt7fHgAEDamz2BvDS38vz/kbU3f+lzmteHxj8mkhRURFCQkJw9uxZ7NixA6GhoWrdb+XKlWjXrh0GDx4MIyMj7N27F9OnT4dSqcSMGTMAAI8fP0b//v1hb2+PuXPnwtraGqmpqdi5c6dqPtHR0QgLC0NgYCCWLFkCALh27RpOnjyJWbNmAQCKi4vh7++PBw8eYNq0aXB1dcWpU6cwb948pKenY/ny5dWybd68GQUFBZg2bRo4jsN//vMfDB8+HLdv34ZEIsHo0aMxZ84c/Prrr/jggw+q3ffXX39F//79YWNjAwA4cuQIQkJC4Ovri88++wwikUhVoLGxsejWrVu1+48aNQqtWrXCl19+CZ7n0blzZzx8+BDR0dH45ZdfajyP06ZNw/r16zFx4kS88847uHPnDr7//nskJCTg5MmTkEgkav0+NPGy5wkA/vjjD4wZMwY+Pj746quvkJOTg8mTJ8PFxUWtZfzyyy+YMGECgoODsWTJEhQXF2PlypXo1asXEhISXlpEJ06cwM6dOzF9+nRYWFjgv//9L0aMGIG0tDTY2toCAB49eoTu3burSsfe3h4HDhzA5MmTkZ+fj9mzZ1eb58KFCyGVSvH++++jrKzsuWt5e/fuBQCMGzdOrceqyTJe5ObNmxg5ciQmT56MCRMmYN26dYiMjISvry/atWsHAMjIyEBAQADkcjnmzp0LMzMzrF69GiYmJtXmpc5rEQAmT56M9evXIyQkBFOmTIFcLkdsbCzi4uLQtWtX1XTq/F7qo66veZ3GG6ioqCgeAO/m5sZLJBJ+9+7dz532s88+4599KoqLi2tMFxwczHt4eKj+v2vXLh4Af/bs2efOe9asWbylpSUvl8ufO83ChQt5MzMz/saNG9Vunzt3Li8Wi/m0tDSe53n+zp07PADe1taWz87OVk23Z88eHgC/d+9e1W09evTgfX19q83vzJkzPAD+f//7H8/zPK9UKvlWrVrxwcHBvFKprPbY3d3d+X79+qluq3qOwsLCauSfMWNGjeeP53k+NjaWB8Bv2rSp2u0HDx6scbu/vz/v7++v+n/VY42KinruNFUmTJjAu7m51bivOs+Tj48P36xZM76goEB1W0xMjOpv50UKCgp4a2tr/o033qh2e0ZGBm9lZVXt9tr+xgDwUqmUv3nzpuq2pKQkHgD/3XffqW6bPHky7+TkxD958qTa/V9//XXeyspK9bd69OhRHgDv4eFR69/vs4YNG8YD4HNzc6vdXlJSwmdmZqq+cnJyVD970TJqe4w8/89r8c6dO6rb3NzceAD88ePHVbc9fvyYNzY25v/v//5Pddvs2bN5AHx8fHy16aysrKrNU53X4pEjR3gA/DvvvFPjZ0///av7e3n27+5Fz4Obmxs/YcIE1f/Vfc3rA4PfnPXo0SPIZDI0b968Tvd7+pNOXl4enjx5An9/f9y+fRt5eXkAAGtrawDAvn37UFFRUet8rK2tUVRUhOjo6Ocua/v27ejduzdsbGzw5MkT1VdQUBAUCgWOHz9ebfoxY8ao1iQAoHfv3gCA27dvV5vm/PnzuHXrluq2bdu2wdjYGEOGDAEAJCYmIiUlBWPHjkVWVpZquUVFRQgMDMTx48drrFq/+eabz30ctT0uKysr9OvXr9rj8vX1hbm5OY4ePar2vDTxsufp4cOHuHTpEiIiImBubq6azt/fHz4+Pi+df3R0NHJzcxEWFlbt8YnFYrz66qtqPb6goCB4enqq/t+hQwdYWlqqMvI8j99++w2DBg0Cz/PVlhMcHIy8vDxcuHCh2jwnTJhQ45N6bao2cz392AHgp59+gr29veqrV69eNe6r7jJexNvbW/U7AQB7e3u0adOm2t/x/v370b1792prxPb29tU2sQHqvRZ/++03cByHzz77rMbPnt389LLfS33V9TWvywy+RFatWgWpVIoBAwa8dAfh006ePImgoCCYmZnB2toa9vb2+Pe//w0AqhLx9/fHiBEjMH/+fNjZ2WHIkCGIiopCWVmZaj7Tp09H69atERISgmbNmmHSpEk1tq2mpKTg4MGD1V649vb2CAoKAlC5qv40V1fXav+veqN8ej/DqFGjIBKJsG3bNgCVb0bbt29HSEgILC0tVcsFKt8Qnl322rVrUVZWpnqsVdzd3dV+DlNSUpCXlwcHB4ca8y8sLKzxuLTtZc9T1T6jli1b1rhvbbc9q+r569u3b43Hd/jwYbUe37MZq3JWZczMzERubi5Wr15dYxkTJ04EUPPvQ93fkYWFBYDKfYZPGzFiBKKjoxEdHY0OHTrUet+6/B08z8seO1D5O2rVqlWN6dq0aVPt/+q8Fm/dugVnZ2c0adJEK9nqo66veV1m8PtEvL29sX//fgQGBqJfv344efLkS9dKbt26hcDAQHh5eWHZsmVo3rw5pFIp9u/fj2+//Vb16ZzjOOzYsQNxcXHYu3cvDh06hEmTJuGbb75BXFwczM3N4eDggMTERBw6dAgHDhzAgQMHEBUVhYiICGzYsAFA5c6+fv36Yc6cObXmad26dbX/i8XiWqfjn7rSsbOzM3r37o1ff/0V//73vxEXF4e0tDTVfpmq5QLA119/jU6dOtU6z2c/pdbl06dSqYSDgwM2bdpU68/t7e3VnhdQ+XzztVzN+XnHMajzPNVH1fP3yy+/wNHRscbP1RmN9bKMVcsYN24cJkyYUOu0z77Rq/s78vLyAgBcvnwZfn5+qtubN2+ueo1UfVJ+Vm3LeN7O5Mb4/ajzWqwLdbLV9fE+ra6veV1m8CUCAN26dcPu3bsxcOBA9OvXD7GxsS98A9u7dy/Kysrw+++/V/tE8rzNE927d0f37t2xaNEibN68GeHh4di6dSumTJkCoHL46qBBgzBo0CAolUpMnz4dq1atwieffIKWLVvC09MThYWFqk8h2jJmzBhMnz4dycnJ2LZtG0xNTTFo0CDVz6tW1y0tLeu17Oe9mDw9PfHnn3/Cz8+v3ps+gMo3tNo2J9Q2Ck0dbm5uACp38D6rttueVfX8OTg4aP13V8Xe3h4WFhZQKBRaX0ZoaCgWL16MTZs2VSsRTVWt6eXm5qo2LwGa/36Ayt9R1Rrf0563VeFFr0VPT08cOnQI2dnZaq2NvIyNjQ1yc3Nr3K7O422o1zwLBr85q0pgYCC2bNmCmzdvYsCAAc8d9gj88ynk6U8deXl5iIqKqjZdTk5OjU9NVZ/oq1ajs7Kyqv1cJBKpPjlWTTN69GjVcMtn5ebmQi6Xq/MQaxgxYgTEYjG2bNmC7du3IzQ0tNpxHb6+vvD09MTSpUtrbNIAKjelqKNqns++oEaPHg2FQoGFCxfWuI9cLq/1Bfginp6euH79erVcSUlJNYYjq8vZ2Rnt27fH//73v2qP/9ixY7h06dJL7x8cHAxLS0t8+eWXtW6HV/f5exGxWIwRI0bgt99+w+XLl7W6DD8/P/Tr1w+rV6/Gnj17ap2mLmsFVaX69Pb8oqIi1Rq3Jl577TXExcXhzJkzqtsyMzNrrN2q81ocMWIEeJ6v9cBYTdZ+PD09kZeXh4sXL6puS09Px65du15634Z6zbMgiDWRKsOGDcOaNWswadIkDB48GAcPHoRMJqsxXf/+/VVrD9OmTUNhYSHWrFkDBwcHpKenq6bbsGEDfvzxRwwbNgyenp4oKCjAmjVrYGlpiddeew0AMGXKFGRnZ6Nv375o1qwZ7t69i++++w6dOnVC27ZtAQAffPABfv/9d4SGhqqGOBYVFeHSpUvYsWMHUlNTYWdnV+fH6+DggICAACxbtgwFBQUYM2ZMtZ+LRCKsXbsWISEhaNeuHSZOnAgXFxc8ePAAR48ehaWlpWoY6Iv4+voCAN555x0EBwdDLBbj9ddfh7+/P6ZNm4avvvoKiYmJ6N+/PyQSCVJSUrB9+3asWLECI0eOVPvxTJo0CcuWLUNwcDAmT56Mx48f46effkK7du1e+KHgRb788ksMGTIEfn5+mDhxInJycvD999+jffv2tRbr0ywtLbFy5UqMHz8eXbp0weuvvw57e3ukpaXhjz/+gJ+fH77//nuNcj1t8eLFOHr0KF599VW88cYb8Pb2RnZ2Ni5cuIA///wT2dnZGs9748aNGDBgAIYOHYqQkBAEBQXBxsYGGRkZ+PPPP3H8+HG1D8zt378/XF1dMXnyZHzwwQcQi8VYt26d6jnRxJw5c/DLL79gwIABmDVrlmqIr5ubW7U3b3VeiwEBARg/fjz++9//IiUlBQMGDIBSqURsbCwCAgLqfL6s119/HR9++CGGDRuGd955RzW8u3Xr1jUGOzyroV7zTDAYEdYoqoYV1jbkb+nSpTwAPjQ0lK+oqKh1SN7vv//Od+jQgZfJZHyLFi34JUuW8OvWras2rPDChQt8WFgY7+rqyhsbG/MODg58aGgof+7cOdV8duzYwffv3593cHDgpVIp7+rqyk+bNo1PT0+vtryCggJ+3rx5fMuWLXmpVMrb2dnxPXv25JcuXcqXl5fzPP/P0NWvv/66xmMCwH/22Wc1bl+zZg0PgLewsOBLSkpqfa4SEhL44cOH87a2tryxsTHv5ubGjx49mv/rr79U01Q9R5mZmTXuL5fL+bfffpu3t7fnOY6r8VyuXr2a9/X15U1MTHgLCwvex8eHnzNnDv/w4UPVNOoM8eV5nt+4cSPv4eHBS6VSvlOnTvyhQ4eeO8RX3edp69atvJeXF29sbMy3b9+e//333/kRI0bwXl5etT5fzzp69CgfHBzMW1lZ8TKZjPf09OQjIyOr/R08b4jvjBkzaszv2eGgPM/zjx494mfMmME3b96cl0gkvKOjIx8YGMivXr26Wg4A/Pbt29XKXaWkpIRfvnw536NHD97S0pI3MjLiHR0d+dDQUH7Tpk3Vhqe/bBnnz5/nX331VdXf+rJly547xHfgwIE17l/bMO6LFy/y/v7+vEwm411cXPiFCxfyP//8c51fizxf+bf69ddf815eXrxUKuXt7e35kJAQ/vz586pp6vJ7OXz4MN++fXteKpXybdq04Tdu3KjWEF+eV+81rw84ntfSXkZCDEinTp1gb2//wqHZhBAB7RMhpDYVFRU1tj/HxMQgKSnppadhIYQAtCZCBC01NRVBQUEYN24cnJ2dcf36dfz000+wsrLC5cuXtXKKC0IMmaB2rBPyLBsbG/j6+mLt2rXIzMyEmZkZBg4ciMWLF1OBEKIGWhMhhBCiMdonQgghRGNUIoQQQjRGJUIIIURjVCKEEEI0RiVCCCFEY1QihBBCNEYlQgghRGNUIoQQQjRGJUIIIURjVCKEEEI0RiVCCCFEY1QihBBCNEYlQgghRGNUIoQQQjRGJUIIIURjVCKEEEI0RiVCCCFEY1QihBBCNEYlQgghRGNUIoQQQjRGJUIIIURjVCKEEEI0RiVCCCFEY1QihBBCNEYlQgghRGNUIoQQQjRGJUIIIURjVCKEEEI0RiVCCCFEY1QihBBCNEYlQgghRGNUIoQQQjRGJUIIIURjVCKEEEI0RiVCCCFEY1QihBBCNEYlQgghRGNUIoQQQjRGJUIIIURjRqwDEMJaaYUCj/PL8LigFHklFSgqV6CkXI7icsXfX39/X6ZAuUIJjgPEHAcjMQcRx8FIxEEkqvxXLBLBTCqGtZkU1iYSWJtKYG0irfzXVAILmYT1wyVEq6hEiMHLyCvFzceFuPOkEOl5pXj0d2E8yq/8Pq+kotGyGIk4NDGTopmNCZo3MUVzG1M0b/LP987WJhCLuEbLQ0h9cTzP86xDEFJfSiWPu9nFuPm48J+vzELcflyIgjI563hqMxJxcLY2gae9GbycLOHlaIG2TpbwtDenciE6iUqE6KXsonIkpOUgIS0XF9JycPF+Hgr1qCzqSiYRwcvREj4uVvBxsUInV2u0cjAHx1GxELaoRIjO43ke19ILcP5uNi6k5SIhLQepWcWsYzFnayZFN/cm6O5hi+4etmjdlEqFND4qEaKTsvKLcORGNk7cfIKTN5/gSWE560g6r6pUXnVvAr+WdmjV1IJ1JCIAVCJEN/A88OACcOMgcOMg0sVO6HFrAutUes3N1hT92jZF/3aO6OpmAxHtUyENgEqEsKOoAFKigev7Kv8teqz6EW9sCa+CH1GmpEOZtMHWTIrAtg7o5+2I3q3sIJOIWUciBoJKhDS+9CQgcTNwaTtQnPXcyT62+Rob010aMZgwmErF8G9tj6GdXdDXywESMRU10RyVCGkchZnAxW1A0hbg0WW17nK2+SSMSglq4GDCZmsmxZBOLhjVtRnaOlmyjkP0EJUIaTjycuDGASBxC3AzGlDWbQhusZ0PvO/Pa6Bw5FneTpYY6dsMQzu7oImZlHUcoieoRIj2PUwEEjcBl3YAJdkaz4YHh/7itUgpMtFeNvJSUrEIgW0dENmzBV71sGUdh+g4KhGiPTcOASe+BdJOa22Wm5z/jY9ut9fa/Ejd+LhYYXIvdwzs4ET7TgCkpqbC3d0dCQkJ6NSpE+s4OoH+Kkj9KBXAxe3ASj9g82itFggA/EuUpNX5kbq59CAPs7cloveSo/gx5ibyihvvPGN1cfz4cQwaNAjOzs7gOA67d+/WaD7P3reiogJhYWFwcXHB5cvq7csTGioRopmKUuDsWuC7LsDOKWrvLK8rl6w4iDllg8ybqC8jvxT/OZiMHov/wie7LyP1SRHrSNUUFRWhY8eO+OGHH7Q2z+LiYgwePBhnz57FiRMn0L49rRHXhkqE1E1pPhC7DFjRAfjj/4Cc1AZdnKgkC0McMht0GUR9xeUK/BJ3F4HLjuGD7Um4l60bp58JCQnBF198gWHDhmllfrm5uejXrx8ePnyIEydOwN3dvdbpFAoFJk+eDHd3d5iYmKBNmzZYsWJFtWliYmLQrVs3mJmZwdraGn5+frh79y4AICkpCQEBAbCwsIClpSV8fX1x7tw51X1PnDiB3r17w8TEBM2bN8c777yDoiLdKnA6FTxRT+FjIO5H4Ow6oCyvURc9wvI6dj5q2qjLJC+mUPLYfv4+dic+wOiuzfF231ZwtJKxjqUVGRkZ8Pf3h7m5OY4dOwZra+vnTqtUKtGsWTNs374dtra2OHXqFKZOnQonJyeMHj0acrkcQ4cOxRtvvIEtW7agvLwcZ86cUZ3jLDw8HJ07d8bKlSshFouRmJgIiaTymjO3bt3CgAED8MUXX2DdunXIzMzEzJkzMXPmTERFRTXGU6EW2rFOXqy8qHLN4/QPgLyESYRCB1+0T/s/Jssm6jE2EmHsq66Y3qcl7C2MmWbhOA67du3C0KFDNbqvVCqFh4cHzp8/D1NT02o/V2fH+syZM5GRkYEdO3YgOzsbtra2iImJgb+/f41pLS0t8d1332HChJqn+JkyZQrEYjFWrVqluu3EiRPw9/dHUVERZDLdKG3anEVqx/NA0lbgO18gdimzAgEAs8xEuMjKmC2fvFyZXImok6n413+OYvGB6416oS9tCw0NxY0bN6q9eb/IDz/8AF9fX9jb28Pc3ByrV69GWloaAKBJkyaIjIxEcHAwBg0ahBUrViA9PV113/feew9TpkxBUFAQFi9ejFu3bql+lpSUhPXr18Pc3Fz1FRwcDKVSiTt37mj3QdcDlQip6d5ZYG0QsGsaUJD+8ukbGMcrMNExlXUMooaSCgV+OnYLfZfGYOuZNCiV+rehY/z48Vi3bh3ef/99LFu27IXTbt26Fe+//z4mT56Mw4cPIzExERMnTkR5+T9nnY6KisLp06fRs2dPbNu2Da1bt0ZcXBwA4PPPP8eVK1cwcOBAHDlyBN7e3ti1axcAoLCwENOmTUNiYqLqKykpCSkpKfD09Gy4J6COaJ8I+Uf+Q+DPz4GLvwLQrRd/oFESvkAb1jGImrKKyjF35yVsPpOG+YPbobOrDetIdTJhwgSIRCJMnDgRSqUS77//fq3TnTx5Ej179sT06dNVtz29NlGlc+fO6Ny5M+bNm4cePXpg8+bN6N69OwCgdevWaN26Nd59912EhYUhKioKw4YNQ5cuXXD16lW0bNmyYR6kltCaCKkcrnvsa+C7rpXnt9KxAgEA15w41hGIBi7ez8Pwlafw/vYkZBY03CbJwsJC1ad1ALhz5w4SExNVm5UAYN68eYiIiFB7nuPHj8eGDRswd+5cfP3117VO06pVK5w7dw6HDh3CjRs38Mknn+Ds2bOqn9+5cwfz5s3D6dOncffuXRw+fBgpKSlo27YtSkpKMHPmTMTExODu3bs4efIkzp49i7Zt2wIAPvzwQ5w6dQozZ85EYmIiUlJSsGfPHsycOVODZ6jh0JqI0F3eCUR/BuSlvXxahsRFGQixf4IDmXaso5A64nlgx/n7OHQlA7MCWyGyZwsYafno93PnziEgIED1//feew9A5RrF+vXrAQDp6enVSkUd4eHhEIlEGD9+PJRKJcaMGVPt59OmTUNCQgLGjBkDjuMQFhaG6dOn48CBAwAAU1NTXL9+HRs2bEBWVhacnJwwY8YMTJs2DXK5HFlZWYiIiMCjR49gZ2eH4cOHY/78+QCADh064NixY/joo4/Qu3dv8DwPT0/PGhlYo9FZQpV3H9gzA7gdwzqJ2o40n4FJKX6sY5B6autkiaWjOqCdsxXrKEQLaHOWECVtBX7sqVcFAgC+5edZRyBacC09H0N/OInlf95AhYLORqDvaE1ESIqygH2zgWu/s06iEV4sRbeKNcgsl7COQrSknbMllo7qSNcy0WO0JiIUNw4BK3vobYEAAKcoR4TjXdYxiBZdeZiPwd+fwH//SoGc1kr0EpWIoSsrBH5/u/IMu4WPWKept/7GdCZVQ1Oh4LEs+gaG/XgKNx4VsI5D6og2Zxmyu6eB3W82+EkSG5Pc0hUtHy9mHYM0EGMjET4d5I3wV91YRyFqohIxRPJy4OgXwKnvAN7wNhFMMP0Bx7L16+A1UjehHZzw1XAfWMho/5euo81ZhiY/HYgaAJxcYZAFAgCvN7nBOgJpYPsupiP0uxO48rBxzxhN6o5KxJDcPw+s7gM8MOyhsN0UCawjkEZwN6sYI1aewq/n7rGOQl6ANmcZiqStwN5ZgLyUdZIGxxuZoEPpKhTI6YQLQjGma3PMH9IOMomYdRTyDFoT0XdKJXDoo8oz7gqgQACAk5dgvON91jFII9p27h7C1sThSSFdEkDXUInos9K8yqG7p79nnaTRhZhcYR2BNLKEtFwM/eEkUmgYsE6hEtFXT24CawKBm9GskzDRpiCedQTCwP2cEgxfeQqxKZmso5C/UYnoo5Q/gbV9gawU1kmYkebeRBcr+kQqRAWlckyMOovN8bp95mmhoBLRN6d/qNyEVUpDHyPshFuiQidX8vj3rkv4Yt9Vvbx6oiGhEtEnfy0EDv0b4BWsk+iEHjwN9RW6tSfu4M2N51Emp9cEK1Qi+uLQR0DsUtYpdIrDk3iYiOnNQ+gOX32EyevPoaSc/hZYoBLRdTwP/PF/ghyB9TJceSFeb/qQdQyiA07cfIKIdfEoKK1gHUVwqER0mVJZeQbes2tZJ9FZg8yuso5AdMTZ1ByMWxuP3OJy1lEEhUpEVykVlQcQJvzCOolOa1t8lnUEokOS7ufh9dVxyCyggxIbC5WILlJUADsmApd+ZZ1E55lkXUVb82LWMYgOuZ5RgDGrTyMjTxhncGCNSkTXyMuAbeOBq3tYJ9EbExxusY5AdMztzCKMWnUK6XklrKMYPL0okZiYGHAch9zcXNZRGlZFCbDldeDGAdZJ9Epvjob6kpruZZdg/M9nkF1E+0gaUr1K5KuvvsIrr7wCCwsLODg4YOjQoUhOTq7TPFJTU8FxHBITE1W3FRQUICAgAN7e3rh/XyAn2lPIga1jgVtHWCfRO05Z8ZCI6IAzUtPNx4WIjDqDwjI56ygGq14lcuzYMcyYMQNxcXGIjo5GRUUF+vfvj6KiIo3nmZmZiYCAABQVFSE2NhbNmjWrT0T9sXcWFYiGRKU5GNE0g3UMoqMu3s/DlA1nUVpBx5E0hHqVyMGDBxEZGYl27dqhY8eOWL9+PdLS0nD+vGYXRbp37x569+4NKysrHDlyBLa2trVOl5WVhbCwMLi4uMDU1BQ+Pj7YsmVLtWl27NgBHx8fmJiYwNbWFkFBQapyi4mJQbdu3WBmZgZra2v4+fnh7t27qvvu2bMHXbp0gUwmg4eHB+bPnw+5vAE/ycQsBhI3Ntz8BWCo+TXWEYgOi7udjZmbEyBXGObVPlnS6j6RvLzK8zk1adKkzvdNTk6Gn58fvL29sX//fpibmz932tLSUvj6+uKPP/7A5cuXMXXqVIwfPx5nzpwBAKSnpyMsLAyTJk3CtWvXEBMTg+HDh4PnecjlcgwdOhT+/v64ePEiTp8+jalTp4LjOABAbGwsIiIiMGvWLFy9ehWrVq3C+vXrsWjRIg2eETUkbARivmqYeQuITwkN9SUv9ue1R5jz20XQdfi0S2tXNlQqlRg8eDByc3Nx4sQJte+XmpoKd3d3SKVS+Pn5ITo6GmJx9auXxcTEICAgADk5ObC2tq51PqGhofDy8sLSpUtx4cIF+Pr6IjU1FW5ubtWmy87Ohq2tLWJiYuDv719jPkFBQQgMDMS8efNUt23cuBFz5szBw4daPjr65l+VJ1NU0vba+uI5EQKwFqklMtZRiI6b5OeOTwd5s45hMLS2JjJjxgxcvnwZW7du1ej+gwcPRmxsLHbu3PnSaRUKBRYuXAgfHx80adIE5ubmOHToENLSKk8N3bFjRwQGBsLHxwejRo3CmjVrkJOTA6ByLSkyMhLBwcEYNGgQVqxYgfT0dNW8k5KSsGDBApibm6u+3njjDaSnp6O4WIvHI2RcAn6dQAWiJRyvRKTjHdYxiB5Yd/IOfom7+/IJiVq0UiIzZ87Evn37cPToUY13hH/00Uf49NNPMXbsWPz664sPsvv666+xYsUKfPjhhzh69CgSExMRHByM8vLKoXxisRjR0dE4cOAAvL298d1336FNmza4c6fyTSYqKgqnT59Gz549sW3bNrRu3RpxcXEAgMLCQsyfPx+JiYmqr0uXLiElJQUymZY+5ebdBzaNAsrpehjaFCBOYh2B6In5v1/BqVtPWMcwCPUqEZ7nMXPmTOzatQtHjhyBu7t7vcJ88skn+PzzzxEeHo5t27Y9d7qTJ09iyJAhGDduHDp27AgPDw/cuHGj2jQcx8HPzw/z589HQkICpFIpdu3apfp5586dMW/ePJw6dQrt27fH5s2bAQBdunRBcnIyWrZsWeNLJNJC55bmVRZIQfrLpyV10jz7NDiOtneTl5MreUzfdAF3szQfSUoqGdXnzjNmzMDmzZuxZ88eWFhYICOjcpillZUVTExMAAARERFwcXHBV1+pt/P4o48+glgsRnh4OJRKJcLCwmpM06pVK+zYsQOnTp2CjY0Nli1bhkePHsHbu3I7Z3x8PP766y/0798fDg4OiI+PR2ZmJtq2bYs7d+5g9erVGDx4MJydnZGcnIyUlBREREQAAD799FOEhobC1dUVI0eOhEgkQlJSEi5fvowvvviiPk9X5elMto0DHtNJAxuCqDgTg+wz8ftjB9ZRiB7ILa7A5A3nsGt6T1jIJKzj6K16lcjKlSsBAH369Kl2e1RUFCIjIwEAaWlpdf4EP3fuXIhEIowfPx48z8PZ2bnazz/++GPcvn0bwcHBMDU1xdSpUzF06FDV6DBLS0scP34cy5cvR35+Ptzc3PDNN98gJCQEjx49wvXr17FhwwZkZWXByckJM2bMwLRp0wAAwcHB2LdvHxYsWIAlS5ZAIpHAy8sLU6ZM0eAZesa+2cCd4/WfD3mukVbJVCJEbTcfF+LtLQlYN+EViEQc6zh6SWujs8hLXPgF+H0m6xQGL9/hFXRIe5d1DKJnpvRyx8ehNGJLE3px7iy9l3EZ2P8B6xSCYPEkAY7GdK4kUjdrT9zBnsQHrGPoJSqRhlaaD/waAcjpbKKNgVPKEemYyjoG0UMf7bqM1Ce0o72uqEQa2u8zgWw6VXljCpJeYh2B6KHCMjne3pKAcjmdGqUuqEQa0pk1dF0QBlrkxrGOQPTUpQd5WHzgOusYeoVKpKE8ugoc/ph1CkEyKniAINts1jGInlp38g7+uvaIdQy9QSXSECpKgd8mA3K6PCcrY2zqdl0bQp72/vYkuryumqhEGsLhj+mAQsa6yi+wjkD0WE5xBd7ZmgCFko6AeBkqEW1LPgicXcM6heBZZ56DjYRObkk0d+ZONtbE3mYdQ+dRiWhTcTYdUKgjOEUZIhzTWMcgeu7b6Bu4Q8N+X4hKRJv+/AwoymSdgvxtgOwy6whEz5XJlfhwB13I6kWoRLQlLa7y1CZEZ7TMj2cdgRiAM6nZ2EjXH3kuKhFtUFQA+94FQJ9WdIkk7w562OSxjkEMwJKDyXiQS2edqA2ViDac/p5GY+mocNsbL5+IkJcoLJPjo110JoTaUInUV85d4Nh/WKcgz9FdkcA6AjEQMcmZ2HnhPusYOodKpL72fwBUaPHa60SrbJ+chZmRgnUMYiAW7ruKvJIK1jF0CpVIfVz9HUg5xDoFeQGuogjhjvTpkWhHTnEFVvyZwjqGTqES0VRZAXDgQ9YpiBoGmtD+KqI9v8Sl4lZmIesYOoNKRFNHvwQKHrJOQdTgVXiGdQRiQCoUPBb9cY11DJ1BJaKJjEtA/CrWKYiajHOS0cGSPjkS7Tly/TGO36ADiwEqEc38tRDgaWetPomwu8k6AjEwC/ddpRM0gkqk7u6fo53peqgXl8g6AjEwKY8LsSmejmSnEqmro4tYJyAaaPokDsYiuuwp0a5vo28gv1TYQ36pROri7mng1hHWKYgGuLJ8jHZMZx2DGJic4gqsjb3DOgZTVCJ1QWshem2IGQ31JdoXdeIOcovLWcdghkpEXXeOA6mxrFOQemhXfJZ1BGKACsrkWH1cuBevohJR19EvWScg9STLuoJWZnQmVqJ9G06lIqdImGsjVCLquPkXkHaadQpSTxx4RDa9xToGMUBF5Qr8fEKY+0aoRNRB+0IMxr9ESawjEAO14XSqIEdqUYm8TPJB4MF51imIlrhkxUHM0VBfon0FpXJsOJnKOkajoxJ5mWNLWCcgWiQqycIwh8esYxADFXUqFaUVwjqbBZXIi9w/Dzy8wDoF0bLhltdZRyAGKruoHL8nCevErFQiL3LuZ9YJSAPoUHqOdQRiwDacSmUdoVFRiTxPSQ5weSfrFKQBmD1JQjNZGesYxEBdeZiPs6nZrGM0GiqR50nYBMjpmAJDxPEKTHQU5nBM0jjWC2hthEqkNjwPnFvHOgVpQH2NLrKOQAzYocsZyMgrZR2jUVCJ1OZ2DJBNB6UZMtecONYRiAGTK3lsjBPGaeKpRGpDO9QNnrgoAyH2T1jHIAZsy5k0lMkNf7gvlciz8tOB5AOsU5BGMNqahvqShpNVVI5DVx6xjtHgqESedWEDoJSzTkEaQZdyOhMBaVi7Ex6wjtDgqESeppAD5zewTkEaiWXmBdhLhXeuI9J4jt/IRFahYQ8npxJ52o2DQIGwjjYVMk5ZgQmOwtj5SdiQK3nsNfAj2KlEnnaFDi4Umn7Gl1hHIAZuVyKViDDIy4GUaNYpSCPzzItnHYEYuKR7ubjzpIh1jAZDJVLldgxQls86BWlkRvlp8G+SwzoGMXC7DHgHO5VIlet7WScgjIQ1ucE6AjFwhjxKi0oEAJRKOjZEwLrJ6XT/pGGlZRfj0v081jEaBJUIANyLA4oyWacgjNg8OQtLIzo2iDSsv64b5oGHVCIAcI02ZQkZJy/FeKf7rGMQA3fkumFeUZNKBACu7WOdgDAWIrvMOgIxcJce5OFxgeGd2ZdKJD0JyEtjnYIw1rqAhvqShsXzwFEDXBuhEqG1EAJAmnsLXa0KWMcgBu6va1Qihof2h5C/jbNLYR2BGLiTN5+gXK5kHUOrhF0iufeAzGusUxAd0ZNPYB2BGLiicgXibmexjqFVwi6RNLq6HfmH/ZM4mIgN/yJChK1jNwzrcAJhl8g9KhHyD668CGGOhn2yPMLe2dRs1hG0SuAlQiNySHWDTK+yjkAM3NWH+SguN5yDW4VbImUFwCN6wyDVtS06wzoCMXByJY+EtFzWMbRGuCVy/yzA0/ZvUp0s+xramhezjkEMnCFt0hJuiaTRpixSu0iHm6wjEAN3LtVwLj8g3BKh/SHkOXpxiawjEAOXkJYDhZJnHUMrhFkiSgVw/xzrFERHOWXFQyIyjBc40U1F5QpcfWgYF8ETZok8ugKU0ykuSO1EpTkY0TSDdQxi4M7dNYz9IsIsEdqURV5imDmdyYA0rGvptCaiv6hEyEu0LznLOgIxcMkZhrE1RJglkp7EOgHRcaZZl+BhanjXfiC6I+VxIXhe//e9Ca9ElAogJ5V1CqLjOF6JCU1vs45BDFhxuQJp2fp/TJLwSiTvHqAoZ52C6IE+4ousIxADd90ANmkJr0SybrFOQPRE8+zT4Dj939xAdJch7BcRXolk0yYKoh5RcSYG2RvWabuJbqES0Ue0JkLqYKRVMusIxIBdz9D/Yb7CKxFaEyF10LmMhvqShnMvu0TvR2gJsERoTYSoz/xJIpxkNBCDNIxyhRKZBWWsY9SLsEpEqQBy7rJOQfQIp5Qjsmkq6xjEgD3M0+/jkYRVIrl3AWUF6xREzwRKL7GOQAzYw9wS1hHqRVglkkX7Q0jdtciNYx2BGDAqEX1C+0OIBowKHiDI1jDOuEp0z8Nc2pylP/IfsE5A9NQYGxrqSxoGrYnok5Jc1gmInuoqv8A6AjFQD/OoRPRHaR7rBERPWWeeg62UBmUQ7cug0Vl6pEz/jw4lbHCKMkQ43mMdgxigglI56wj1IqwSoTURUg/BxjTUl2hfSYUCcoWSdQyNUYkQoibPfLoiJmkY+rw2IrASoc1ZRHOSvFT0tKEPIkT7qET0Ba2JkHoaa3uDdQRigPJL9XfQhnBKpKIUUOj3ic4Ie90VCawjEANUWEZrIrqPRmYRLbB9cgZmRgrWMYiBoc1Z+oA2ZREt4CqKMd7xPusYxMAU0OYsPUAlQrTkNZMrrCMQA1MmpyG+uq+8iHUCYiDaFJ5hHYEYGKUeX91QOCXCcawTEANhnHMDnSwLWccgBkSppBLRfZxwHippeOPtU1hHIAZEjzsERqwDNBoqEb2m5ESoEEkgN5KiQmyECiMp5GIpKkRiVIglkIskqBCLIRcZVd4mEkP+978VIlHl/zkRKjgOFSIR5ByHCk6ECgAVHAc5h7+/B+QAKsCr/q3glZD//W8FlJDzPN64+BD7r5xj+6QQg2HZbRKAFqxjaIRKRIAqREaVb8YiSeUbcNUbs1jyz5tw1fdiUeW/nOifN2ZOhAoR9/ebctUbMlf9zRhQfV/5ZqxEBc9XvhlD+dQbswJyXokKXoEKpQJyXoEKXo4Kpbzye6UcFcoKKPnn7XhUAij7+6uWHzXA/korXgbHP9LB59OwcaIdpiUFrCNoTEAlItb6LHlwKBdLVW/CcrEUFWLJ399LUCEyqvz+eZ+OOdHfb8pVn46f/mTMoaLqTZjjKj8RP/XpWPXJ+Kk34wpe+fcbslz177NvxgqlAjyet+5c9fb/jKo3Yjo8AgAw9aEX+HxaCyHaw4m1//7UWARTIhlSE6zvHIoKjq/26VgOVNtMUcEr/v5e+c+nZKW88o1Z+dSnZKUcCv5576qN/+mYNJ5XTmSyjkAMjR5vKRFMieRLpdiUe5F1DKLnRuS3AW7TcSJEuzix/paI/iavI5lYxjoCMQBDLujvZgeiu0SmpqwjaEwwJSIVS1lHIHrOp9wBsvjLrGMQAySysGQdQWOCKRFaEyH1NeWGC6CkHVpE+8SWFqwjaEwwJWJsZMw6AtFjVkoZnGOus45BDJTIgkpE55kYmdDaCNHYWw/bgi/Q37H8RLeJqUT0g62JLesIRA9xPOAbm8E6BjFgIkvaJ6IX7EzsWEcgemh0nhf41HusYxADxUmlEBnr7+Z2KhFCXiL0Ap0BmjQcfV4LAahECHmhzuVOMD5Dw3pJw9Hn/SGAwEqE9omQupp03RHQ4wsGEd1nZG/POkK9CKpEaE2E1IWN0gSOx66yjkEMnMTFhXWEehFWicioRIj6pj/wAl9Il1UmDYtKRI/Ym+r3aiNpPBwPdDr+kHUMIgBUInqENmcRdYXleYFPe8A6BhEAiYsz6wj1IqgSsTWxhREnmLPfk3p47RztTCeNQ0prIvpDIpLA1dKVdQyi47qWOUN6jnaok0YgFsOoaVPWKepFUCUCAJ7WnqwjEB0Xed2BhvWSRiFp2hSckX5vHaESIeQpdkozND12jXUMIhD6vlMdEGKJWFGJkOebfq81+CIa1ksah9TDg3WEehNeidCaCHkOMTj4HKcRWaTxyNp6sY5Qb4IrkRaWLWiEFqlVeE5b8Pfp2BDSeGReVCJ6RyKWoLllc9YxiA4KPitnHYEIiUgE4zZtWKeoN8GVCED7RUhNr5a5QHKehvWSxiN1c4PIxIR1jHoTZonQfhHyjMirdEoc0rgMYX8IINASaWnTknUEokMclGawO3aFdQwiMMZebVlH0ApBlkgn+06sIxAdMj2tNfiSEtYxiMDQmogeczRzhLOZfp/0jGiHGBzaHaPrp5PGJ2tLayJ6zbepL+sIRAeMz24L/mEG6xhEYCTNmsHIzjDOKk4lQgSt/5kK1hGIAJm+2o11BK2hEiGC5VfaHEYJdJ4s0vjMulGJ6L0WVi1gK7NlHYMwNP5KE9YRiECZvvoq6whaI9gSAYAuTbuwjkAYcVJYwDaWhvWSxidxc4XE0ZF1DK0RdInQJi3heiutFfiSUtYxiAAZ0qYsQOAl0rVpV9YRCANGvAhtY1JZxyACZdrNcDZlAQIvkVY2rWAhtWAdgzSyiVne4DMes45BBMqQRmYBAi8RESeCn7Mf6xikkfU9Q0enEzak7u6QODiwjqFVgi4RAAh0DWQdgTQi/xI3iJOSWccgAmXepw/rCFon+BLp3aw3pCIp6xikkYRfsWYdgQiYRb9+rCNoneBLxExihledDGtHF6mdi8ISNscvs45BBEpsbweTzp1Yx9A6wZcIAAS5BbGOQBrB9LstwZeVsY5BBMoiMBAcx7GOoXVUIgD6NO8DMSdmHYM0ICkvRuuYO6xjEAGzCDK8TVkAlQgAoImsCTo5dGIdgzSgiU+8wT/KZB2DCJTIygpmBja0twqVyN9olJZh6xNfxDoCETCLPv7gJBLWMRoElcjfqEQMV9/iFhBfusE6BhEw8yDD3e9KJfI3Z3NntG1iGFcaI9WFXbZkHYEImMjMDOa9e7OO0WCoRJ4S6hHKOgLRMje5NaxjaVgvYcfytRCIZDLWMRoMlchThrQcQgceGpg3Uz3Al5ezjkEEzHrkSNYRGhSVyFOsjK3omBEDYsyL0TLmNusYRMCMW7WESceOrGM0KCqRZ4xsbdifGoRkcmY78JlPWMcgAmY1YgTrCA2OSuQZrzi+ghaWLVjHIFrwr7gC1hGIgHESCayGDGEdo8FRidRiRCvD//Rg6PoXeUB0JYV1DCJg5oGBMLKxYR2jwVGJ1GJIyyGQiAzzwCChGHPRjHUEInCGvkO9CpVILWxkNnTwoR7zkNvA4iQN6yXsGDk7waxnD9YxGgWVyHPQDnb9Ne22O1BRwToGEbAmY8eCEwnj7VUYj1ID3Ry7wc3SjXUMUkcy3giex26yjkEETGRhAevXX2cdo9FQiTwHx3GY0G4C6xikjt7I9IbySTbrGETAbMaMhtjcnHWMRkMl8gJDPYeiqWlT1jFIHfQ6lcc6AhEwTiKBTUQE6xiNikrkBSRiCSa2n8g6BlFTSJEHuGu3WMcgAmY5eBAkDg6sYzQqKpGXGNFqBJrImrCOQdQwKsmUdQQiZBwH28mTWadodFQiLyEzkiHCW1irp/qoVYUtzGlYL2HIvG9fGHt4sI7R6KhE1PC61+uwMrZiHYO8wNTbboBczjoGETDbKcJbCwGoRNRiJjFDuFc46xjkOUyVErSIoVOcEHZMX3kFpp07s47BBJWImsa2HQszCZ1KQxdNfewNPjuHdQwiYPbvvss6AjNUImqyMrbCmDZjWMcgtehxigqEsGPu7w/TLsJcCwGoROoksl0kLCQWrGOQpwwqbAkumS48RRjhONi/O5t1CqaoROrARmaDaR2nsY5BnjI80Zh1BCJglgMHQublxToGU1QidTS27Vi6aJWOaFNhB7PTV1jHIALFSaVwEPhaCEAlUmcSkQTvd32fdQwCYOotVxrWS5ixGTcOEhcX1jGYoxLRgH9zf/R07sk6hqCZ81K4Hk1mHYMIlNjKCnZv0qZtgEpEY3NemQMjzoh1DMGaluENPpdOtkjYsHv7bYgtLVnH0AlUIhrytPbEqDajWMcQrFdPPmEdgQiUrH172IwNYx1DZ1CJ1MOMTjPodCgMDC1oBaSkso5BhEgshuP8zwVz1UJ10DNRD1bGVnir41usYwjOsAQp6whEoJqMC4dJu3asY+gUKpF6GtNmDFrbtGYdQzDalTvAJI7O1ksan5GjI+zfeYd1DJ1DJVJPRiIjLPBbADEnZh1FEKbcdAEUCtYxiAA1/ejfEJnR+fOeRSWiBe1s29H12BuBFS9DMxrWSxgwDwiAZb9+rGPoJCoRLZneaTrcrdxZxzBoUx96gc/PZx2DCAxnagrHTz5mHUNnUYloibHYGAt6LoCIo6e0obxyIpN1BCJADv/3HiTOzqxj6Cx6x9OiTg6daLNWAxmZ3wa4fZd1DCIw5v7+aBJOF6R7ESoRLXu709s0WqsBDL5Af6qkcYnt7OD05SLWMXSeTr4yY2JiwHEccnNzWUepM4lYgi97fQmJSMI6isHwKXeALJ7O1ksal/OXi2Bka8s6hs6rU4msXLkSHTp0gKWlJSwtLdGjRw8cOHCgTgtMTU0Fx3FITExU3VZQUICAgAB4e3vj/v37dZqfLmrTpA1mdp7JOobBmHLDBVAqWccgAmITHg7zf/2LdQy9UKcSadasGRYvXozz58/j3Llz6Nu3L4YMGYIrVzT/lJiZmYmAgAAUFRUhNjYWzZo103heuiSyXSS6O3VnHUPvWSllcI65zjoGERDjVi3hMOcD1jH0Rp1KZNCgQXjttdfQqlUrtG7dGosWLYK5uTni4uI0Wvi9e/fQu3dvWFlZ4ciRI7B9zqpjVlYWwsLC4OLiAlNTU/j4+GDLli3VptmxYwd8fHxgYmICW1tbBAUFoaioCEDl5rFu3brBzMwM1tbW8PPzw927/+yk3bNnD7p06QKZTAYPDw/Mnz8f8npep0LEifCff/0HTmZO9ZqP0E1Pbwu+oIB1DCIQnFQK56VLITKmK2aqS+N9IgqFAlu3bkVRURF69OhR5/snJyfDz88P3t7e2L9/P8zNzZ87bWlpKXx9ffHHH3/g8uXLmDp1KsaPH48zZ84AANLT0xEWFoZJkybh2rVriImJwfDhw8HzPORyOYYOHQp/f39cvHgRp0+fxtSpU8FxHAAgNjYWERERmDVrFq5evYpVq1Zh/fr1WLSo/jvUbGQ2+LbPt5CK6FxPmuB4oMvxDNYxiIA4vP8+ZG3asI6hVzie5/m63OHSpUvo0aMHSktLYW5ujs2bN+O1115T+/6pqalwd3eHVCqFn58foqOjIRZXP2VITEwMAgICkJOTA2tr61rnExoaCi8vLyxduhQXLlyAr68vUlNT4ebmVm267Oxs2NraIiYmBv7+/jXmExQUhMDAQMybN09128aNGzFnzhw8fPhQ7cf1Ir/d+A2fn/5cK/MSkjG5Xhixks6TRRqH1ZDBcF6yhHUMvVPnNZE2bdogMTER8fHxeOuttzBhwgRcvXq1zgsePHgwYmNjsXPnzpdOq1AosHDhQvj4+KBJkyYwNzfHoUOHkJaWBgDo2LEjAgMD4ePjg1GjRmHNmjXIyckBADRp0gSRkZEIDg7GoEGDsGLFCqSnp6vmnZSUhAULFsDc3Fz19cYbbyA9PR3FxcV1fly1GdF6BIa3Gq6VeQlJ6AWOdQQiELL27eG4YAHrGHqpzmsizwoKCoKnpydWrVql1vRVayIJCQnYu3cvFixYgE2bNmH06NGqaZ5dE1m8eDGWLl2K5cuXw8fHB2ZmZpg9ezaMjIywe/duAADP8zh16hQOHz6MXbt2ISMjA/Hx8XB3rzwVSUJCAg4ePIi9e/fi0qVLiI6ORvfu3WFiYoL58+dj+PCab/IeHh4Qaem6AeWKckQciMCVLBqqqo7O5U6Yt+w+UL8/T0JeSmxnB/cd2yFxdGQdRS/V+/quSqUSZWVlGt33k08+gUgkQnh4OHiex5gxY2qd7uTJkxgyZAjGjRunWuaNGzfg7e2tmobjOPj5+cHPzw+ffvop3NzcsGvXLrz33nsAgM6dO6Nz586YN28eevTogc2bN6N79+7o0qULkpOT0bJlS40eg7qkYim+7fMtRu8bjdyy3AZdliGYdN0R4O+xjkEMnUSCZiuWU4HUQ51KZN68eQgJCYGrqysKCgqwefNmxMTE4NChQ6ppIiIi4OLigq+++kqteX700UcQi8UIDw+HUqlEWFjNy062atUKO3bswKlTp2BjY4Nly5bh0aNHqhKJj4/HX3/9hf79+8PBwQHx8fHIzMxE27ZtcefOHaxevRqDBw+Gs7MzkpOTkZKSgoiICADAp59+itDQULi6umLkyJEQiURISkrC5cuX8cUXX9Tl6XkpJ3MnLPnXErz151tQ8nTcw/PYKk3heOwqaB2ENDTHjz6Cqa8v6xh6rU4l8vjxY0RERCA9PR1WVlbo0KEDDh06hH5PnSI5LS2tzpuA5s6dC5FIhPHjx4PneTg/c7Kzjz/+GLdv30ZwcDBMTU0xdepUDB06FHl5eQAAS0tLHD9+HMuXL0d+fj7c3NzwzTffICQkBI8ePcL169exYcMGZGVlwcnJCTNmzMC0adMAAMHBwdi3bx8WLFiAJUuWQCKRwMvLC1OmTKnTY1BXT+eemNVlFr49/22DzN8QvPmgDfjCs6xjEANnPWYMbF6vfesHUV+994kQzXwV/xU2X9/MOobO4Xjg181Nwac9YB2FGDDTrl3hGrUOnIROT1RfOnnuLCGY220uBrQYwDqGzgnL86ICIQ3KuHVrNPvxByoQLaESYYTjOHzZ60s6NcozXjtHK8ak4UiaNUPztWsgtrRkHcVgUIkwJBFLsDxgObxtvV8+sQB0LXOG9FzdjzkiRB1iW1u4/rwWEgcH1lEMCpUIY2YSM/wY+CNcLVxZR2Fu4vWmdFwIaRAic3O4rlkN6TNntCD1RyWiA2xNbLGq3yrYmdixjsKMndIMDjF0ICbRPk4qRbPvv4fMm9b4GwKViI5oZtEMPwX9BHPJ809Eacim32sNXkunmSFERSyG89KvYdb9VdZJDBaViA5p06QNvg/8HqZGpqyjNCoxOPgcpxFZRMtEIjgtWADL/v1ZJzFoVCI6xrepL1b3Xw0LqQXrKI0mPKct+PvaOWMyIQAq10CWLIb1CDrxaUOjEtFBHe074uf+P8PG2IZ1lEYRfLZ+FwAjpBqJBC7ffAOrQYNYJxEEKhEd1da2LaIGRMHexJ51lAbVvdQFkvM0rJdoByeVotl/V8ByQDDrKIJBJaLDPK09sX7AeoO+xO6Ea4ZdkqTxcDIZmv34IywCAlhHERQqER3naumKDQM2GORxJA5KM9gdo2G9pP5EpqZovnoVzHv5sY4iOFQiesDJ3AnrB6yHp5Un6yhaNT2tNfiSEtYxiJ4TWVqi+c9rYdatG+sogkQloifsTe0RNSAK7WzbsY6iFWJwaHeMLjpF6kfi6ooWW7fCtHNn1lEEi0pEj9jIbLB+wHoEt9D/nYYR2d7gH2awjkH0mEmXLmixbSuMPdxZRxE0KhE9IzOSYan/UkzvNB0cONZxNNbvTDnrCESPWQ4aBNf1UTCyEcYweF1GJaKn3ur4Fr7p8w1MjExYR6kzv9LmMEq4xjoG0VN2M2fC5ev/QCSVso5CQCWi1/q59cOGARvgaObIOkqdjL/ShHUEooc4qRTOX38N+5kzWEchT6ES0XNtbdtiy8At6GDfgXUUtTgpLGAbS8N6Sd2I7ezguj4KVoNCWUchz6ASMQB2JnaICo7CIA/dP83DW2mtwJeUso5B9Ijpq6/CY9dOmHbpwjoKqQXH83QVIEPyy9Vf8O35b1GhrGAdpQYjXoQt663BZzxmHYXoA5EIdm++CbuZM8CJ6POurqLfjIEZ7z0emwduhoeVB+soNUzM8qYCIWoR29rCde0a2L/zNhWIjqPfjgHyauKFbaHbMLr1aNZRqul7ho5OJy9n2q0b3HfthFnPnqyjEDXQ5iwDdyTtCD479Rlyy3KZ5vAvccOM5beYZiA6TiSC7bSpsJ85E5xYzDoNUROtiRi4vq59sXPwTnR36s40R/gVa6bLJ7pN4uIC13Xr4DBrFhWInqE1EYHgeR4brmzAfxP+2+g73ZvJrfDtfwvBl5U16nKJfrAeMwZN53wAkZkZ6yhEA1QiAnMt6xo+PfUprmdfb7RlLrrVBa1+PdNoyyP6wcjZCU4LF8Lcj07frs+oRARIoVRgy/Ut+D7xexRVFDXosqS8GJuiLME/ymzQ5RA9IhLBZuxYOLw7m9Y+DACViIA9Ln6M/5z9Dw6lHmqwZUzL9EHg2oQGmz/RL9KWnnBauJBO3W5AqEQITj04hUXxi5BWkKb1eW/Z5wHxpRtany/RLyIzM9i+OQ22EyaAoxMnGhQqEQIAKFeU4+dLP2PtpbUoV2rnNO19i1vgzRU3tTIvoqdEIlgNHwaH2bNhZGfHOg1pAFQipJq0/DQsil+EUw9P1Xtea850gNVfF7SQiugj065d0fTf8yDz9mYdhTQgKhFSqxMPTuD7hO9xJUuzM+66ya2xdEU++HK6+JTQSFxc4PDBB7AcoP9X4CQvRwcbklr1cumFraFbsbzPcrS0blnn+7+Z6kEFIjAiCwvYv/suPA7s18sCiYmJAcdxyM3NZR1Fr1CJkBcKdAvEb4N/w+Lei+Fq4arWfYx5MVrG3G7gZERXiKysYDdzJlr+9Sfspk1t0CsOLl68GBzHYfbs2XW6X2pqKjiOQ2Jiouq2goICBAQEwNvbG/fv39duUAExYh2A6D4RJ8JAj4EIbhGMPTf3YNXFVUgvSn/u9JMz24HPpH0hhk5sbY0mkRNgM24cxObmDb68s2fPYtWqVejQof4XYMvMzERISAhEIhFiY2Nha2uLmzdpEIgmaE2EqM1IZIQRrUfgj2F/YG63ubA3sa91un/FFTRyMtKYxDY2sH/vvco1jzffbJQCKSwsRHh4ONasWQMbG5t6zevevXvo3bs3rKyscOTIEdja2tY6XVZWFsLCwuDi4gJTU1P4+Phgy5Yt1abZsWMHfHx8YGJiAltbWwQFBaGoqPIA3piYGHTr1g1mZmawtraGn58f7t69q7rvnj170KVLF8hkMnh4eGD+/PmQy+X1emwsUImQOpOIJQhvG45DIw7hC78v0MamjepnwcUeEF1JYZiONBQje3s4fPBBZXlMfaNRjzafMWMGBg4ciKCgoHrNJzk5GX5+fvD29sb+/fth/oICLC0tha+vL/744w9cvnwZU6dOxfjx43HmTOUpfNLT0xEWFoZJkybh2rVriImJwfDhw8HzPORyOYYOHQp/f39cvHgRp0+fxtSpU8FxHAAgNjYWERERmDVrFq5evYpVq1Zh/fr1WLRoUb0eHws0OotoRVx6HP535X+I/C0PFkdpU5YhMe3aFTbhY2ERFAROImn05W/duhWLFi3C2bNnIZPJ0KdPH3Tq1AnLly9Xex6pqalwd3eHVCqFn58foqOjIX7mbMExMTEICAhATk4OrK2ta51PaGgovLy8sHTpUly4cAG+vr5ITU2Fm5tbtemys7Nha2uLmJgY+Pv715hPUFAQAgMDMW/ePNVtGzduxJw5c/Dw4UO1H5cuoH0iRCu6O3VHd6fuKG+ZihzXLcjdtRvK/HzWsYiGOFNTWA0aBJuxYyFr05pZjnv37mHWrFmIjo6GTCar9/wGDx6M3bt3Y+fOnRg1atQLp1UoFPjyyy/x66+/4sGDBygvL0dZWRlMTU0BAB07dkRgYCB8fHwQHByM/v37Y+TIkbCxsUGTJk0QGRmJ4OBg9OvXD0FBQRg9ejScnJwAAElJSTh58mS1NQ+FQoHS0lIUFxerlqEPaE2ENAhlSQny9u5F7tZtKL16lXUcoiZpixawGRsGq2HDILawYB0Hu3fvxrBhw6qtNSgUCnAcB5FIhLKyshprFLWpWhNJSEjA3r17sWDBAmzatAmjR/9z9c9n10QWL16MpUuXYvny5fDx8YGZmRlmz54NIyMj7N69G0DlJRZOnTqFw4cPY9euXcjIyEB8fDzc3d0BAAkJCTh48CD27t2LS5cuITo6Gt27d4eJiQnmz5+P4cOH18jq4eEBkR5dEpjWREiDEJmYwGb0aNiMHo2ylBTk7d2H/H37UKFnq+pCILKwgEW/frAaFArT7t1V2+11QWBgIC5dulTttokTJ8LLywsffvihWgXyrE8++QQikQjh4eHgeR5jxoypdbqTJ09iyJAhGDduHABAqVTixo0b8H7qCHyO4+Dn5wc/Pz98+umncHNzw65du/Dee+8BADp37ozOnTtj3rx56NGjBzZv3ozu3bujS5cuSE5ORsuWdT8GS9dQiZAGZ9yqFRzeexf2785GyblzyPt9L/IPHaLNXQxxMhnM+/SB5cDXYO7v36DHdtSHhYUF2rdvX+02MzMz2NraVrs9IiICLi4u+Oqrr9Sa70cffQSxWIzw8HAolUqEhYXVmKZVq1bYsWMHTp06BRsbGyxbtgyPHj1SlUh8fDz++usv9O/fHw4ODoiPj0dmZibatm2LO3fuYPXq1Rg8eDCcnZ2RnJyMlJQUREREAAA+/fRThIaGwtXVFSNHjoRIJEJSUhIuX76ML774QtOniwkqEdJoOI6D6SuvwPSVV9D0k49ReOwY8n/fi8LYWPClpazjGT4jI5j59YTVwIEw7xsIsbnhXMsjLS2tzpuA5s6dC5FIhPHjx4PneTg7O1f7+ccff4zbt28jODgYpqammDp1KoYOHYq8vDwAgKWlJY4fP47ly5cjPz8fbm5u+OabbxASEoJHjx7h+vXr2LBhA7KysuDk5IQZM2Zg2rRpAIDg4GDs27cPCxYswJIlSyCRSODl5YUpU6Zo5wlpRLRPhDCnLC1FUVwcio4fR+Gx46h48IB1JIMhtrKCac8eMO/VG+Z9A2BUz2MsCHkWlQjROWU3b6Lw2HEUHj+O4gsXgIrGvSa8XhOJIPNpX1kavXtB5uMDToP9BoSoi0qE6DRFYSGKTp1C8dlzKElMROn161Qqz5C4usLU1xfmvXvBrGdPiJ9zjAMhDYFKhOgVZWkpSi9fRnFCAkoSk1CSmAhFVhbrWI1GZGUFEx8fmHToAJOOHSDr0IE2URGmqESI3itPS0NJUhLKbtxA2a3bKL91C+X37wMKBeto9SK2t4OxWwsYt24FWYcOMOnYEdIWLXRqCC4hVCLEICnLy1Gemory27dRdvMWym/fQtntO5BnZEChQ9eL4ExMIG3RAtIWbjB2d4fU3b3y/+7ujXJiQ0Lqi0qECI6yvByKzEzIMzNR8fe/T38pi4rAl5ZBWVpS+W9ZKfjSMvClpeCf3R8jEoGTSMBJpZVfqu8lEJmZQWxtDSNrG4htbCBu0gRGdnYwcnCAkb09jBzsIba2pjULoteoRAipA16hqDymheMqy8KIDrUiwkYlQgghRGP6c5YvQgghOodKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGiMSoQQQojGqEQIIYRojEqEEEKIxqhECCGEaIxKhBBCiMaoRAghhGjs/wF5Ub/1vcPuPQAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.pie(school.values(), labels=school.keys()) # Setzen der Labels\n",
|
||
"\n",
|
||
"plt.title(\"Klassenverteilung einer Grundschule\")\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "d3e68330-6319-4a87-acda-91abd4f98900",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-5336af155ef45527",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Zum Anzeigen von Prozentwerten im Pie Chart wird der Parameter `autopct` verwendet. \n",
|
||
"\n",
|
||
"Dieser akzeptiert entweder einen **Format-String** oder eine Funktion, mit der die Prozentwerte der einzelnen Segmente definiert werden können. \n",
|
||
"\n",
|
||
"Weitere Informationen findest du in der [Matplotlib-Dokumentation zu autopct](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.pie.html#matplotlib-pyplot-pie) sowie in einer Übersicht zu [Format-Strings](https://www.geeksforgeeks.org/format-specifiers-in-c/). \n",
|
||
"\n",
|
||
"Beispiel für die Darstellung von Prozentwerten:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 54,
|
||
"id": "974a71d0-552c-45d4-bb01-88edd6be608c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-183044afa87a0492",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAGbCAYAAAAFuq0xAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAXvpJREFUeJzt3XlcVPX+x/HXzDDDsIMICiiIuyiuZRp5yRXNNS3N3Je00tZfdfO22t7NSm+r2k29lVpaVppLVuK+7/uOuAAi+77MnN8fJIqgwrCcWT7Px4MHcObMOe8ZmPnM93u+53s0iqIoCCGEEBbQqh1ACCGE7ZIiIoQQwmJSRIQQQlhMiogQQgiLSRERQghhMSkiQgghLCZFRAghhMWkiAghhLCYFBEhhBAWkyICvP7662g0GrVjOLR7772Xe++9t/j3mJgYNBoN8+fPVy1TVZL/sao1f/58NBoNMTExVb5tjUbD1KlTq3SbDRo0YOzYsVW6TWtht0Xk6j/Zrl27SixPS0ujY8eOGI1GVq9erVI6+7Jy5Upef/11tWMIC+Xl5fHJJ59wzz334OPjg8FgIDAwkAEDBrBo0SJMJpPaEYUVs9siUpb09HR69erFgQMHWLZsGb1791Y7kl1YuXIl06dPr9Q2fv/9d37//fcqSmR9Xn75ZXJyctSOUUpiYiIRERE8+eSTuLu78/LLLzN79myeeOIJsrKyePjhh3nnnXfUjimsmJPaAWpKRkYGUVFR7Nu3j59++ok+ffqoHcnmZWVl4ebmViXbMhgMVbIda+Xk5ISTU82/3HJzczEYDGi1ZX9eHDVqFHv37uXHH39k8ODBJW6bNm0au3bt4vjx45Xah7BvDvFXz8zMpHfv3uzZs4cff/yRvn373vY+8+bNo1u3bvj7++Ps7ExYWBhffPFFqfV27dpFVFQUtWvXxsXFhdDQUMaPH19incWLF9OhQwc8PDzw9PQkPDycWbNmlVgnNTWVp59+mvr16+Ps7Ezjxo15//33MZvNxetcPU4wY8YM5syZQ6NGjXB2dubOO+9k586dxevNmDEDjUbDuXPnSuWdNm0aBoOBlJSU4mXbt2+nd+/eeHl54erqSmRkJJs3by5xv6t9+keOHOHhhx/Gx8eHe+65h7Fjx/LZZ58BRX3JV7+uMpvNzJw5k5YtW2I0GqlTpw6TJ08usX8ofUykLDdbZ+zYsTRo0KDCz9NVS5YsISwsDKPRSKtWrVi2bFmpbd7KqlWr6NKlC25ubnh4eNC3b18OHz5cYp2yjolc7Xv/+eefadWqFc7OzrRs2bLMbtaLFy8yfvx46tSpU7ze119/XWKd6OhoNBoNixcv5uWXXyYoKAhXV1fS09PLzL1161bWrFnDpEmTShWQq+644w5GjBhRrn3c7LhPWccvGjRoQL9+/di0aVNx93LDhg353//+V+r+hw8fplu3bri4uFCvXj3eeuutEq+Lq8rzWjSbzcyaNYvw8HCMRiN+fn707t27VLc3cNu/y83+R8p7/Ks8r3lbYPctkaysLPr06cPOnTtZunQp/fr1K9f9vvjiC1q2bMmAAQNwcnJi+fLlPP7445jNZqZMmQLA5cuX6dWrF35+frz44ot4e3sTExPDTz/9VLydtWvXMnz4cLp37877778PwNGjR9m8eTNPPfUUANnZ2URGRnLx4kUmT55McHAwW7ZsYdq0acTFxTFz5swS2RYuXEhGRgaTJ09Go9Hw73//m8GDB3PmzBn0ej1Dhw7lhRde4IcffuD5558vcd8ffviBXr164ePjA8Bff/1Fnz596NChA6+99hparba4gG7cuJGOHTuWuP+DDz5IkyZNeOedd1AUhXbt2nHp0iXWrl3LN998U+p5nDx5MvPnz2fcuHE8+eSTnD17lk8//ZS9e/eyefNm9Hp9uf4elrjd8wTw22+/MWzYMMLDw3n33XdJSUlhwoQJBAUFlWsf33zzDWPGjCEqKor333+f7OxsvvjiC+655x727t1720K0adMmfvrpJx5//HE8PDz4z3/+w5AhQ4iNjcXX1xeAhIQEOnXqVFx0/Pz8WLVqFRMmTCA9PZ2nn366xDbffPNNDAYDzz33HHl5eTdt5S1fvhyAkSNHluuxWrKPWzl16hQPPPAAEyZMYMyYMXz99deMHTuWDh060LJlSwDi4+Pp2rUrhYWFvPjii7i5uTFnzhxcXFxKbKs8r0WACRMmMH/+fPr06cPEiRMpLCxk48aNbNu2jTvuuKN4vfL8XSqjoq95q6bYqXnz5imAEhISouj1euXnn3++6bqvvfaacuNTkZ2dXWq9qKgopWHDhsW/L1u2TAGUnTt33nTbTz31lOLp6akUFhbedJ0333xTcXNzU06cOFFi+YsvvqjodDolNjZWURRFOXv2rAIovr6+SnJycvF6v/zyiwIoy5cvL17WuXNnpUOHDiW2t2PHDgVQ/ve//ymKoihms1lp0qSJEhUVpZjN5hKPPTQ0VOnZs2fxsqvP0fDhw0vlnzJlSqnnT1EUZePGjQqgfPfddyWWr169utTyyMhIJTIysvj3q4913rx5N13nqjFjxighISGl7lue5yk8PFypV6+ekpGRUbwsOjq6+H/nVjIyMhRvb2/lkUceKbE8Pj5e8fLyKrG8rP8xQDEYDMqpU6eKl+3fv18BlE8++aR42YQJE5SAgADlypUrJe7/0EMPKV5eXsX/q+vWrVMApWHDhmX+/97o/vvvVwAlNTW1xPKcnBwlMTGx+CslJaX4tlvto6zHqCjXXotnz54tXhYSEqIAyoYNG4qXXb58WXF2dlb+7//+r3jZ008/rQDK9u3bS6zn5eVVYpvleS3+9ddfCqA8+eSTpW67/v+/vH+XG//vbvU8hISEKGPGjCn+vbyveVtg991ZCQkJGI1G6tevX6H7Xf9JJy0tjStXrhAZGcmZM2dIS0sDwNvbG4AVK1ZQUFBQ5na8vb3Jyspi7dq1N93XkiVL6NKlCz4+Ply5cqX4q0ePHphMJjZs2FBi/WHDhhW3JAC6dOkCwJkzZ0qss3v3bk6fPl287Pvvv8fZ2ZmBAwcCsG/fPk6ePMnDDz9MUlJS8X6zsrLo3r07GzZsKNW0fvTRR2/6OMp6XF5eXvTs2bPE4+rQoQPu7u6sW7eu3NuyxO2ep0uXLnHw4EFGjx6Nu7t78XqRkZGEh4ffdvtr164lNTWV4cOHl3h8Op2Ou+66q1yPr0ePHjRq1Kj499atW+Pp6VmcUVEUfvzxR/r374+iKCX2ExUVRVpaGnv27CmxzTFjxpT6pF6Wq91c1z92gC+//BI/P7/ir3vuuafUfcu7j1sJCwsr/psA+Pn50axZsxL/xytXrqRTp04lWsR+fn4lutigfK/FH3/8EY1Gw2uvvVbqthu7n273d6msir7mrZndF5HZs2djMBjo3bv3bQ8QXm/z5s306NEDNzc3vL298fPz41//+hdAcRGJjIxkyJAhTJ8+ndq1azNw4EDmzZtHXl5e8XYef/xxmjZtSp8+fahXrx7jx48v1bd68uRJVq9eXeKF6+fnR48ePYCipvr1goODS/x+9Y3y+uMMDz74IFqtlu+//x4oejNasmQJffr0wdPTs3i/UPSGcOO+v/rqK/Ly8oof61WhoaHlfg5PnjxJWloa/v7+pbafmZlZ6nFVtds9T1ePGTVu3LjUfctadqOrz1+3bt1KPb7ff/+9XI/vxoxXc17NmJiYSGpqKnPmzCm1j3HjxgGl/z/K+zfy8PAAio4ZXm/IkCGsXbuWtWvX0rp16zLvW5H/g5u53WOHor9RkyZNSq3XrFmzEr+X57V4+vRpAgMDqVWrVpVkq4yKvuatmd0fEwkLC2PlypV0796dnj17snnz5tu2Sk6fPk337t1p3rw5H330EfXr18dgMLBy5Uo+/vjj4k/nGo2GpUuXsm3bNpYvX86aNWsYP348H374Idu2bcPd3R1/f3/27dvHmjVrWLVqFatWrWLevHmMHj2aBQsWAEUH+3r27MkLL7xQZp6mTZuW+F2n05W5nnLdlY4DAwPp0qULP/zwA//617/Ytm0bsbGxxcdlru4X4IMPPqBt27ZlbvPGT6kV+fRpNpvx9/fnu+++K/N2Pz+/cm8Lip5vpYyrOd/sPIbyPE+VcfX5++abb6hbt26p28szGut2Ga/uY+TIkYwZM6bMdW98oy/v36h58+YAHDp0iIiIiOLl9evXL36NXP2kfKOy9nGzg8k18fcpz2uxIsqTraKP93oVfc1bM7svIgAdO3bk559/pm/fvvTs2ZONGzfe8g1s+fLl5OXl8euvv5b4RHKz7olOnTrRqVMn3n77bRYuXMiIESNYvHgxEydOBIqGr/bv35/+/ftjNpt5/PHHmT17Nq+88gqNGzemUaNGZGZmFn8KqSrDhg3j8ccf5/jx43z//fe4urrSv3//4tuvNtc9PT0rte+bvZgaNWrEH3/8QURERKW7PqDoDa2s7oSyRqGVR0hICFB0gPdGZS270dXnz9/fv8r/dlf5+fnh4eGByWSq8n3069eP9957j++++65EEbHU1ZZeampqcfcSWP73gaK/0dUW3/Vu1qtwq9dio0aNWLNmDcnJyeVqjdyOj48PqamppZaX5/FW12teDXbfnXVV9+7dWbRoEadOnaJ37943HfYI1z6FXP+pIy0tjXnz5pVYLyUlpdSnpquf6K82o5OSkkrcrtVqiz85Xl1n6NChxcMtb5SamkphYWF5HmIpQ4YMQafTsWjRIpYsWUK/fv1KnNfRoUMHGjVqxIwZM0p1aUBRV0p5XN3mjS+ooUOHYjKZePPNN0vdp7CwsMwX4K00atSIY8eOlci1f//+UsORyyswMJBWrVrxv//9r8TjX79+PQcPHrzt/aOiovD09OSdd94psx++vM/freh0OoYMGcKPP/7IoUOHqnQfERER9OzZkzlz5vDLL7+UuU5FWgVXi+r1/flZWVnFLW5L3HfffWzbto0dO3YUL0tMTCzVui3Pa3HIkCEoilLmibGWtH4aNWpEWloaBw4cKF4WFxfHsmXLbnvf6nrNq8EhWiJX3X///cydO5fx48czYMAAVq9ejdFoLLVer169ilsPkydPJjMzk7lz5+Lv709cXFzxegsWLODzzz/n/vvvp1GjRmRkZDB37lw8PT257777AJg4cSLJycl069aNevXqce7cOT755BPatm1LixYtAHj++ef59ddf6devX/EQx6ysLA4ePMjSpUuJiYmhdu3aFX68/v7+dO3alY8++oiMjAyGDRtW4natVstXX31Fnz59aNmyJePGjSMoKIiLFy+ybt06PD09i4eB3kqHDh0AePLJJ4mKikKn0/HQQw8RGRnJ5MmTeffdd9m3bx+9evVCr9dz8uRJlixZwqxZs3jggQfK/XjGjx/PRx99RFRUFBMmTODy5ct8+eWXtGzZ8pYfCm7lnXfeYeDAgURERDBu3DhSUlL49NNPadWqVZmF9Xqenp588cUXjBo1ivbt2/PQQw/h5+dHbGwsv/32GxEREXz66acW5bree++9x7p167jrrrt45JFHCAsLIzk5mT179vDHH3+QnJxs8ba//fZbevfuzaBBg+jTpw89evTAx8eH+Ph4/vjjDzZs2FDuE3N79epFcHAwEyZM4Pnnn0en0/H1118XPyeWeOGFF/jmm2/o3bs3Tz31VPEQ35CQkBJv3uV5LXbt2pVRo0bxn//8h5MnT9K7d2/MZjMbN26ka9euFZ4v66GHHuKf//wn999/P08++WTx8O6mTZuWGuxwo+p6zatChRFhNeLqsMKyhvzNmDFDAZR+/fopBQUFZQ7J+/XXX5XWrVsrRqNRadCggfL+++8rX3/9dYlhhXv27FGGDx+uBAcHK87Ozoq/v7/Sr18/ZdeuXcXbWbp0qdKrVy/F399fMRgMSnBwsDJ58mQlLi6uxP4yMjKUadOmKY0bN1YMBoNSu3Zt5e6771ZmzJih5OfnK4pybejqBx98UOoxAcprr71WavncuXMVQPHw8FBycnLKfK727t2rDB48WPH19VWcnZ2VkJAQZejQocqff/5ZvM7V5ygxMbHU/QsLC5UnnnhC8fPzUzQaTanncs6cOUqHDh0UFxcXxcPDQwkPD1deeOEF5dKlS8XrlGeIr6Ioyrfffqs0bNhQMRgMStu2bZU1a9bcdIhveZ+nxYsXK82bN1ecnZ2VVq1aKb/++qsyZMgQpXnz5mU+Xzdat26dEhUVpXh5eSlGo1Fp1KiRMnbs2BL/Bzcb4jtlypRS27txOKiiKEpCQoIyZcoUpX79+oper1fq1q2rdO/eXZkzZ06JHICyZMmScuW+KicnR5k5c6bSuXNnxdPTU3FyclLq1q2r9OvXT/nuu+9KDE+/3T52796t3HXXXcX/6x999NFNh/j27du31P3LGsZ94MABJTIyUjEajUpQUJDy5ptvKv/9738r/FpUlKL/1Q8++EBp3ry5YjAYFD8/P6VPnz7K7t27i9epyN/l999/V1q1aqUYDAalWbNmyrfffluuIb6KUr7XvC3QKEoVHWUUwo60bdsWPz+/Ww7NFkI40DERIcpSUFBQqv85Ojqa/fv333YaFiEESEtEOLSYmBh69OjByJEjCQwM5NixY3z55Zd4eXlx6NChKpniQgh75lAH1oW4kY+PDx06dOCrr74iMTERNzc3+vbty3vvvScFRIhykJaIEEIIi8kxESGEEBaTIiKEEMJiUkSEEEJYTIqIEEIIi0kREUIIYTEpIkIIISwmRUQIIYTFpIgIIYSwmBQRIYQQFpMiIoQQwmJSRIQQQlhMiogQQgiLSRERQghhMSkiQgghLCZFRAghhMWkiAghhLCYFBEhhBAWkyIihBDCYlJEhBBCWEyKiBBCCItJERFCCGExKSJCCCEsJkVECCGExaSICCGEsJgUESGEEBaTIiKEEMJiUkSEEEJYTIqIEEIIi0kREUIIYTEpIkIIISwmRUQIIYTFpIgIIYSwmBQRIYQQFpMiIoQQwmJSRIQQQlhMiogQQgiLSRERQghhMSkiQgghLCZFRAghhMWc1A4ghNpyC0xcTs/jckYuaTkFZOWbyMkvJDvf9PfX3z/nmcg3mdFoQKfR4KTToNVocNJq0GqLvuu0WtwMOrzdDHi76PF21ePtYij67qrHw6hX++EKUaWkiAi7F5+Wy6nLmZy9kklcWi4JfxeMhPSin9NyCmosi5NWQy03A/V8XKhfy5X6Pq7Ur3Xt50BvF3RaTY3lEaKyNIqiKGqHEKKyzGaFc8nZnLqcee0rMZMzlzPJyCtUO165OWk1BHq70MjPjeYBnjSv60GLAE8a+blLcRFWSYqIsEnJWfnsjU1hb2wqe2JTOHAhjUwbKhYVZdRraV7Xk/AgL8KDvGgb7E0Tf3c0GiksQl1SRITVUxSFo3EZ7D6XzJ7YVPbGphCTlK12LNX5uhnoGFqLTg196dTQl6Z1pKiImidFRFilpPQs/jqRzKZTV9h86gpXMvPVjmT1rhaVu0JrEdG4Nk3qeKgdSTgAKSLCOigKXNwDJ1bDidXE6QLofHqM2qlsWoivKz1b1KFXy7rcEeKDVo6piGogRUSox1QAJ9fCsRVF37MuF9+kOHvSPONz8sxyKlNV8HUz0L2FPz3D6tKlSW2Mep3akYSdkCIial7cfti3EA4ugeykm672ss8HfBsXVIPBHIOrQUdkUz8GtQuiW3N/9Dop1MJyUkREzchMhAPfw/5FkHCoXHfZWX88D57sUc3BHJuvm4GBbYN48I56tAjwVDuOsEFSRET1KcyHE6tg3yI4tRbMFRuCm107nLAL06opnLhRWIAnD3Sox6B2QdRyM6gdR9gIKSKi6l3aB/u+g4NLISfZ4s0oaOil+4qTWS5Vl03clkGnpXsLf8be3YC7GvqqHUdYOSkiouqcWAObPobYrVW2ye8C/8VLZ1pV2fZExYQHeTHhnlD6tg6QYydATEwMoaGh7N27l7Zt26odxyrIf4WoHLMJDiyBLyJg4dAqLSAA/9Dur9LtiYo5eDGNp7/fR5f31/F59CnSsmtunrGK2LBhA/379ycwMBCNRsPPP/9s0XZuvG9BQQHDhw8nKCiIQ4fKdyzP0UgREZYpyIWdX8En7eGnieU+WF5RQUnb0GnM1bJtUX7x6bn8e/VxOr/3J6/8fIiYK1lqRyohKyuLNm3a8Nlnn1XZNrOzsxkwYAA7d+5k06ZNtGolLeKySBERFZObDhs/glmt4bf/g5SYat2dNieJgf6J1boPUX7Z+Sa+2XaO7h+t5/kl+zmfbB3Tz/Tp04e33nqL+++/v0q2l5qaSs+ePbl06RKbNm0iNDS0zPVMJhMTJkwgNDQUFxcXmjVrxqxZs0qsEx0dTceOHXFzc8Pb25uIiAjOnTsHwP79++natSseHh54enrSoUMHdu3aVXzfTZs20aVLF1xcXKhfvz5PPvkkWVnWVcBlKnhRPpmXYdvnsPNryEur0V0P8TzGTwl1anSf4tZMZoUluy/w876LDL2jPk90a0JdL6PasapEfHw8kZGRuLu7s379ery9vW+6rtlspl69eixZsgRfX1+2bNnCpEmTCAgIYOjQoRQWFjJo0CAeeeQRFi1aRH5+Pjt27Cie42zEiBG0a9eOL774Ap1Ox759+9Dri645c/r0aXr37s1bb73F119/TWJiIlOnTmXq1KnMmzevJp6KcpED6+LW8rOKWh5bP4PCHFUiZPp3oFXs/6myb1E+zk5aHr4rmMfvbYyfh7OqWTQaDcuWLWPQoEEW3ddgMNCwYUN2796Nq6tridvLc2B96tSpxMfHs3TpUpKTk/H19SU6OprIyMhS63p6evLJJ58wZkzpKX4mTpyITqdj9uzZxcs2bdpEZGQkWVlZGI3WUbSlO0uUTVFg/2L4pANsnKFaAQFwS9xHkDFPtf2L28srNDNvcwz/+Pc63lt1rEYv9FXV+vXrx4kTJ0q8ed/KZ599RocOHfDz88Pd3Z05c+YQGxsLQK1atRg7dixRUVH079+fWbNmERcXV3zfZ599lokTJ9KjRw/ee+89Tp8+XXzb/v37mT9/Pu7u7sVfUVFRmM1mzp49W7UPuhKkiIjSzu+Er3rAssmQEXf79auZRjExrm6M2jFEOeQUmPhy/Wm6zYhm8Y5YzGbb6+gYNWoUX3/9Nc899xwfffTRLdddvHgxzz33HBMmTOD3339n3759jBs3jvz8a7NOz5s3j61bt3L33Xfz/fff07RpU7Zt2wbA66+/zuHDh+nbty9//fUXYWFhLFu2DIDMzEwmT57Mvn37ir/279/PyZMnadSoUfU9ARUkx0TENemX4I/X4cAPgHW9+Ls77ectmqkdQ5RTUlY+L/50kIU7Ypk+oCXtgn3UjlQhY8aMQavVMm7cOMxmM88991yZ623evJm7776bxx9/vHjZ9a2Jq9q1a0e7du2YNm0anTt3ZuHChXTq1AmApk2b0rRpU5555hmGDx/OvHnzuP/++2nfvj1HjhyhcePG1fMgq4i0RETRcN31H8AndxTNb2VlBQQgOGWb2hGEBQ5cSGPwF1t4bsl+EjOqr0syMzOz+NM6wNmzZ9m3b19xtxLAtGnTGD16dLm3OWrUKBYsWMCLL77IBx98UOY6TZo0YdeuXaxZs4YTJ07wyiuvsHPnzuLbz549y7Rp09i6dSvnzp3j999/5+TJk7Ro0YKcnBymTp1KdHQ0586dY/PmzezcuZMWLVoA8M9//pMtW7YwdepU9u3bx8mTJ/nll1+YOnWqBc9Q9ZGWiKM79BOsfQ3SYm+/rop0WfH08bvCqsTaakcRFaQosHT3BdYcjuep7k0Ye3cDnKr47Pddu3bRtWvX4t+fffZZoKhFMX/+fADi4uJKFJXyGDFiBFqtllGjRmE2mxk2bFiJ2ydPnszevXsZNmwYGo2G4cOH8/jjj7Nq1SoAXF1dOXbsGAsWLCApKYmAgACmTJnC5MmTKSwsJCkpidGjR5OQkEDt2rUZPHgw06dPB6B169asX7+el156iS5duqAoCo0aNSqVQW0yOstRpV2AX6bAmWi1k5TbX/WnMP5khNoxRCW1CPBkxoOtaRnopXYUUQWkO8sR7V8Mn99tUwUEoEP+brUjiCpwNC6dQZ9tZuYfJygwyWwEtk5aIo4kKwlWPA1Hf1U7iUUUnYGOBXNJzNerHUVUkZaBnsx4sI1cy8SGSUvEUZxYA190ttkCAqAx5TO67jm1Y4gqdPhSOgM+3cR//jxJobRKbJIUEXuXlwm/PlE0w25mgtppKq2Xs8ykam8KTAofrT3B/Z9v4URChtpxRAVJd5Y9O7cVfn602idJrEmFnsE0vvye2jFENXF20vJq/zBG3BWidhRRTlJE7FFhPqx7C7Z8Aor9dRGMcf2M9cm2dfKaqJh+rQN4d3A4HkY5/mXtpDvL3qTHwbzesHmWXRYQgIdqnVA7gqhmKw7E0e+TTRy+VLMzRouKkyJiTy7shjn3wkX7Hgrb0bRX7QiiBpxLymbIF1v4Ydd5taOIW5DuLHuxfzEsfwoKc9VOUu0UJxda584mo1AmXHAUw+6oz/SBLTHqdWpHETeQloitM5thzUtFM+46QAEB0BTmMKruBbVjiBr0/a7zDJ+7jSuZckkAayNFxJblphUN3d36qdpJalwfl8NqRxA1bG9sKoM+28xJGQZsVaSI2Korp2Budzi1Vu0kqmiWsV3tCEIFF1JyGPzFFjaeTFQ7ivibFBFbdPIP+KobJJ1UO4lqDKmnaO8ln0gdUUZuIePm7WThduueedpRSBGxNVs/K+rCypWhj6NrO24RdXSFZoV/LTvIWyuO2OTVE+2JFBFb8uebsOZfoJjUTmIVOisy1NfRfbXpLI9+u5u8QnlNqEWKiK1Y8xJsnKF2Cqvif2U7Ljp583B0vx9JYML8XeTky/+CGqSIWDtFgd/+zyFHYN2OJj+Th+pcUjuGsAKbTl1h9NfbycgtUDuKw5EiYs3M5qIZeHd+pXYSq9Xf7YjaEYSV2BmTwsivtpOana92FIciRcRamU1FJxDu/UbtJFatRfZOtSMIK7L/QhoPzdlGYoaclFhTpIhYI1MBLB0HB39QO4nVc0k6Qgv3bLVjCCtyLD6DYXO2Ep/mGDM4qE2KiLUpzIPvR8GRX9ROYjPG+J9WO4KwMmcSs3hw9hbi0nLUjmL3bKKIREdHo9FoSE1NVTtK9SrIgUUPwYlVaiexKV00MtRXlHY+OYdR/91BcpYcI6lOlSoi7777LnfeeSceHh74+/szaNAgjh8/XqFtxMTEoNFo2LdvX/GyjIwMunbtSlhYGBcuOMhEe6ZCWPwwnP5L7SQ2JyBpO3qtnHAmSjt1OZOx83aQmVeodhS7Vakisn79eqZMmcK2bdtYu3YtBQUF9OrVi6ysLIu3mZiYSNeuXcnKymLjxo3Uq1evMhFtx/KnpIBYSJubwpA68WrHEFbqwIU0Ji7YSW6BnEdSHSpVRFavXs3YsWNp2bIlbdq0Yf78+cTGxrJ7t2UXRTp//jxdunTBy8uLv/76C19f3zLXS0pKYvjw4QQFBeHq6kp4eDiLFi0qsc7SpUsJDw/HxcUFX19fevToUVzcoqOj6dixI25ubnh7exMREcG5c+eK7/vLL7/Qvn17jEYjDRs2ZPr06RQWVuMnmej3YN+31bd9BzDI/ajaEYQV23YmmakL91Joss+rfaqpSo+JpKUVzedUq1atCt/3+PHjREREEBYWxsqVK3F3d7/purm5uXTo0IHffvuNQ4cOMWnSJEaNGsWOHTsAiIuLY/jw4YwfP56jR48SHR3N4MGDURSFwsJCBg0aRGRkJAcOHGDr1q1MmjQJjUYDwMaNGxk9ejRPPfUUR44cYfbs2cyfP5+3337bgmekHPZ+C9HvVs+2HUh4jgz1Fbf2x9EEXvjxAHIdvqpVZVc2NJvNDBgwgNTUVDZt2lTu+8XExBAaGorBYCAiIoK1a9ei05W8ell0dDRdu3YlJSUFb2/vMrfTr18/mjdvzowZM9izZw8dOnQgJiaGkJCQEuslJyfj6+tLdHQ0kZGRpbbTo0cPunfvzrRp04qXffvtt7zwwgtculTFZ0ef+rNoMkWz9NdWlqLR0pWviMkxqh1FWLnxEaG82j9M7Rh2o8paIlOmTOHQoUMsXrzYovsPGDCAjRs38tNPP912XZPJxJtvvkl4eDi1atXC3d2dNWvWEBtbNDV0mzZt6N69O+Hh4Tz44IPMnTuXlJQUoKiVNHbsWKKioujfvz+zZs0iLi6ueNv79+/njTfewN3dvfjrkUceIS4ujuzsKjwfIf4g/DBGCkgV0ShmxtY9q3YMYQO+3nyWb7adu/2KolyqpIhMnTqVFStWsG7dOosPhL/00ku8+uqrPPzww/zww61Psvvggw+YNWsW//znP1m3bh379u0jKiqK/PyioXw6nY61a9eyatUqwsLC+OSTT2jWrBlnzxa9ycybN4+tW7dy99138/3339O0aVO2bdsGQGZmJtOnT2ffvn3FXwcPHuTkyZMYjVX0KTftAnz3IOTL9TCqUlfdfrUjCBsx/dfDbDl9Re0YdqFSRURRFKZOncqyZcv466+/CA0NrVSYV155hddff50RI0bw/fff33S9zZs3M3DgQEaOHEmbNm1o2LAhJ06cKLGORqMhIiKC6dOns3fvXgwGA8uWLSu+vV27dkybNo0tW7bQqlUrFi5cCED79u05fvw4jRs3LvWl1VZBzc1NKyogGXG3X1dUSP3krWg00t8tbq/QrPD4d3s4l2T5SFJRxKkyd54yZQoLFy7kl19+wcPDg/j4omGWXl5euLi4ADB69GiCgoJ4993yHTx+6aWX0Ol0jBgxArPZzPDhw0ut06RJE5YuXcqWLVvw8fHho48+IiEhgbCwon7O7du38+eff9KrVy/8/f3Zvn07iYmJtGjRgrNnzzJnzhwGDBhAYGAgx48f5+TJk4wePRqAV199lX79+hEcHMwDDzyAVqtl//79HDp0iLfeeqsyT1fRdCbfj4TLMmlgddBmJ9LfL5FfL/urHUXYgNTsAiYs2MWyx+/Gw6hXO47NqlQR+eKLLwC49957SyyfN28eY8eOBSA2NrbCn+BffPFFtFoto0aNQlEUAgMDS9z+8ssvc+bMGaKionB1dWXSpEkMGjSoeHSYp6cnGzZsYObMmaSnpxMSEsKHH35Inz59SEhI4NixYyxYsICkpCQCAgKYMmUKkydPBiAqKooVK1bwxhtv8P7776PX62nevDkTJ0604Bm6wYqn4eyGym9H3NQDXseliIhyO3U5kycW7eXrMXei1WrUjmOTqmx0lriNPd/Ar1PVTmH30v3vpHXsM2rHEDZm4j2hvNxPRmxZwibmzrJ58Ydg5fNqp3AIHlf2UtdZ5koSFfPVprP8su+i2jFskhSR6pabDj+MhkKZTbQmaMyFjK0bo3YMYYNeWnaImCtyoL2ipIhUt1+nQrJMVV6TehgOqh1B2KDMvEKeWLSX/EKZGqUipIhUpx1z5bogKmiQuk3tCMJGHbyYxnurjqkdw6ZIEakuCUfg95fVTuGQnDIu0sM3We0YwkZ9vfksfx5NUDuGzZAiUh0KcuHHCVAol+dUyzCfil3XRojrPbdkv1xet5ykiFSH31+WEwpVdkfhHrUjCBuWkl3Ak4v3YjLLGRC3I0Wkqh1fDTvnqp3C4Xkn7sJHL5NbCsvtOJvM3I1n1I5h9aSIVKXsZDmh0EpoTHmMrhurdgxh4z5ee4KzMuz3lqSIVKU/XoOsRLVTiL/1Nh5SO4KwcXmFZv65VC5kdStSRKpK7LaiqU2E1Wicvl3tCMIO7IhJ5lu5/shNSRGpCqYCWPEMIJ9WrIk+7SydfdLUjiHswPurj3MxVWadKIsUkaqw9VMZjWWlRvieuP1KQtxGZl4hLy2TmRDKIkWkslLOwfp/q51C3EQn0161Iwg7EX08kZ/2XFA7htWRIlJZK5+Hgiq89rqoUr5XduLmZFI7hrATb644QlpOgdoxrEqlLkrl8I78CifXqJ1C3IKmIIsRdS8w50KI2lGqXNrWH8g+sZWC5AtonAw4B7XAJ3Iset96xesUpMSRsu6/5F04gmIqwCW0A7V6Tkbn5lO+fWxbQur6BXh0GECtHpOKlyf/OZesQ3+i0RvxjhyDe8uuxbdlHdtE1qE/8X/gtap7sFYiJbuAWX+c5NX+cu2Rq6QlYqm8DFj1T7VTiHLo62Kfx6tyzx/Co31f6o6cQZ1hb4KpkIQfXsGcXzRdhzk/l8s/vAIaDXWGv0PdkR+gmAu5/OMbKMrtZ6rNiztBxr7V6P0alFiefWo7WUfX4z/0TXzuHUfy6k8wZRcNYDDnZZG64X/U6vVYlT9ea/HNthhOJ2aqHcNqSBGx1Lp3IOOS2ilEOTTP3KF2hGpRZ+gbuIf3wOAXgsG/Ib59n8GUnkh+wikA8i4eoTDtMrXvewaDXwMMfg2o3fcZ8uNOkXvuwC23bc7P4cryGfj2fgKt0b3EbQVJ5zHWD8c5oAluYZFoDK4UphVNWJiybh4e7e7DydN+L1FcYFJ4+7ejasewGlJELBF/ELbPVjuFKCfnlOO09rT/T47mvKIzq6++6Sumor57jU5fvI5GZwCNhrwLh2+5reS1X+DS6E5cGrQtdZvBL5T8+FOYcjPJiz+FUpiHk08guRcOk59wGo8O/avoEVmvv45dZsMJObEYpIhY5s83QZGDtbZkdO1TakeoVopiJuXPuTgHhWH4u/vJObA5Gr2RlOh5mAtyMefnkrLuv6CYMWWm3HRbWUfWkx9/Gp/IMWXe7tKwA24t7yV+wTMk/fYxtfs+g1bvTPKaz6kVNYWMvSu5OHcy8d8+T36i/Z6k9+aKIzJBI3JgveIu7JKD6TboHs0+oK3KKapP8u9fkJ94jrojrg0317l64TfoRZJ//5yM3ctBo8EtLBJDnUag0ZS5ncL0RJL/nEudYW+icTLcdH/e94zA+54Rxb+nblqIsUFbNFodaVu/J3D8Z+Sc2kHSbx8RMHZW1T1QK3LycibfbT/H6M4N1I6iKikiFbXubbUTCAvUubINZ+1o8sz21/hOXvsFOad3Uufh93DyrF3iNpfQ9gRN/gpTdhoarQ6t0Z3zn47E1btumdvKjz+FOTuVuPlPXVuomMk7f5iMPSsIfm4ZGq2uxH0Kks6TdWQdAWP/Q+aBtRjrtULn6oVr8y4krZqFOS8brbNrlT9ua/Dx2hMMaheEp1F/+5XtlBSRiji3FU7/pXYKYQFNXjpD68bxzaUgtaNUGUVRSPnjS7JPbKXO8HfR36QwQFGrBCDn3H7MWWm4Nr6rzPWMIW0IGP9piWVJK2eh962H511DShUQRVFIWvMZPt0mojW4gGJGMf89Bf/V7+UYCWarUrIL+GrjWZ7t2VTtKKqxv49l1UlaITZtoJt9DfVNXvsFmYejqd3/ebQGV0yZKZgyUzAX5BWvk3lgLXkXj1GQEkfm4XVc+fk9PO4cWOJckoTF/yJ993IAtM6uxSO5rn5p9M5ojR7Fx1qul7l/DToXz+Ki5BzUgtxzB8i7eIz0nb+g9w0uNbrL3szbdJbU7Hy1Y6hGWiLldXYDxGxUO4WohJbZO4GeaseoMpl7VwKQsGhaieW+9z2Ne3gPAAqSL5KyYQHmnEycvPzx6jwUjzsHlVi/ICUe55z0Cu/flJVC2tYfqDvyg+JlzoHN8Ox4P5eXTkfr6kXtvs9UeLu2JiOvkDkbzvBC7+ZqR1GFRpGJ8svn694Qu1XtFKISFDT00n3FySwXtaMIO+Nm0LHpn93wcbv5YAR7Jd1Z5XHqTykgdkCDwtg6p9WOIexQVr6J/246q3YMVUgRKQ85FmI3/qHdr3YEYacWbI0hPdfxJmeUInI7x1fDxd1qpxBVJChpGzqN/Y4WEurJyC1kweYYtWPUOCkit7P+fbUTiCqkzUnifv/LascQdmrelhhyCxxrNgspIrdyYTdc2qN2ClHFBnseUzuCsFPJWfn8ut+xJmaVInIru/6rdgJRDVrn7lI7grBjC7bEqB2hRkkRuZmcFDj0k9opRDVwu7Kfesa8268ohAUOX0pnZ0yy2jFqjBSRm9n7HRTmqJ2i3N7dmMedczPxeDcd/w8yGLQ4m+NXSvbNztmdz73zs/B8Nx3N9HRSc8t3itBnO/JpMDMD41vp3PVVJjsultzus2tyqfV+OvU/zuC7AyVHpyw5XED/RdZ1+WCNYmJcXcccjilqxnwHao1IESmLosCur9VOUSHrzxUy5U4D2ya4sXaUKwVm6PVtNln51wpFdoFC78ZO/KuLc7m3+/2hAp79PZfXIp3ZM9mNNnV0RH2bxeWsohFOy48XsPBgAb+PcuPfPYxMXJ7Dleyi29JyFV76K4/P7jNW7YOtAt2cbn1RJiEqY82heOLTctWOUSOkiJTlTDQk29ZJaatHujG2rYGW/jra1NUxf6CR2DSF3XHXWg1Pd3LmxXuc6VRPd4stlfTRtjweaa9nXDsDYX46vuxnxFWv4eu9RS2Oo1fM3NtAxx2BOoaH6/F01nA2pahwvbA2l8fu0BPsZX3/ZsEp29SOIOxYoVnh2232ey2V61nfq9sa2MEB9bS/u/xruZR93YjyyDcp7L5kpkfDa1OsaTUaejR0YuuFouLUpo6OXZdMpOQo7L5kIqdAoXEtLZtiC9kTb+LJu6xzGghdVjx9/K6oHUPYsUU7YskrtP/hvlJEbpQeB8dXqZ2iUsyKwtOrc4mor6OVf/lbHTe6kq1gUqCOW8lCVMdNQ3xmUZdVVGMnRrbWc+fcTMb+ksOCQS64GeCx33L5sq8LX+wqoNmnmUR8ncXhy9b1ghrqLUN9RfVJyspnzeEEtWNUOykiN9qz4Np1EGzUlN9yOXTZxOIHamaiwdfvNXLqSQ8OPubO/S30vLsxnx6hTuh18NaGPDaNc2ViOz2jf7augQrt82UmAlG9ft57Ue0I1U6KyPVMhbB7gdopKmXqyhxWnCxk3Rg36nlW7s9b21WDTgMJWSVHcSVkKdR1L3vbx66Y+PZgAW92cyY6ppB/hOjwc9MytKWePXFmMvKsZ9Joz8Q9+Bkcb64jUXM2nEgkKdO+h5NLEbneidWQYZtnmyqKwtSVOSw7Vshfo10J9an8n9ag09AhUMufZ661zMyKwp9nCulcxsF5RVGYvCKXj3o5427QYDJDwd/TVF39brKeGoLGXMCYuo5x8FOoo9CssNzOz2CXInK9w7Z7cuGUlbl8e6CAhYNd8HAuOmYRn2kmp+Dau3Z8ppl98SZOJRe9ox9MMLEv3kRyzrV1uv8vi093XLtK27OdnJm7p4AF+/I5mmjisRW5ZBUojGtb+prSX+0pwM9VQ/9mRbdFBDvx19lCtl0o5OOteYT5afE2Wn6gvzr0dD6odgRh55bts+8iIlc2vKowH06uVTuFxb7YVdQtc++Ckif2zRtoZGzbohFSX+7KZ/r6awXiH/OzS61zOtlcfJ4HwLBWehKzFV6NziM+U6FtXS2rR7hS54burIRMM29vzGPLBLfiZR2DdPxfZ2f6LszB303DgkHWdzGoRmnbgfvVjiHs2P7zqZy9kkVobbfbr2yD5MqGV534HRY+qHYKoYIxrp+xPtlH7RjCjj3ZvQnP9myqdoxqId1ZVx1brnYCoZLhtU6oHUHYOXsepSVFBMBstvlzQ4TlOhbKdP+iesUmZ3PwQpraMaqFFBGA89sgK1HtFEIlPld24ulk2+cGCev35zH7PPFQigjAUenKcmSawlxGBVxQO4awc38ds88rakoRATi6Qu0EQmV9jIfUjiDs3MGLaVzOsL+ZfaWIxO2HtFi1UwiVNc3YrnYEYecUBdbZYWtEioi0QgRgSD3NHV4ZascQdu7Po1JE7I8cDxF/G1n7pNoRhJ3bfOoK+YXm269oQxy7iKSeh8SjaqcQVuJuZa/aEYSdy8o3se1MktoxqpRjF5FYubqduMbvyjZcdNZ1zRNhf9afsK/TCRy7iJyXIiKu0eRnMbyufU+WJ9S3MyZZ7QhVysGLiIzIESX1dz2idgRh545cSic7335ObnXcIpKXAQnyhiFKapG1Q+0Iws4VmhX2xqaqHaPKOG4RubATFOn/FiUZk4/Swj379isKUQn21KXluEUkVrqyRNnG+p9SO4Kwc7tiUtSOUGUct4jI8RBxE/do9qkdQdi5vbEpmMz2cSknxywiZhNc2KV2CmGlApK2o9faxwtcWKesfBNHLqWrHaNKOGYRSTgM+TLFhSibNjeFIXXi1Y4h7Nyuc/ZxXMQxi4h0ZYnbuN9dZjIQ1etonLREbJcUEXEbrXJ2qh1B2Lnj8fbRG+KYRSRuv9oJhJVzTTpIQ1f7u/aDsB4nL2eiKLZ/7M3xiojZBCkxaqcQVk6jmBlT54zaMYQdy843EZts++ckOV4RSTsPpny1UwgbcK/ugNoRhJ07ZgddWo5XRJJOq51A2Ij6yVvRaGy/u0FYL3s4LuJ4RSRZuihE+WizE+nvZ1/TdgvrIkXEFklLRFTAA17H1Y4g7NixeNsf5ut4RURaIqIC2uXJUF9Rfc4n59j8CC0HLCLSEhHl535lHwFGGYghqke+yUxiRp7aMSrFsYqI2QQp59ROIWyIxlzI2DoxascQduxSmm2fj+RYRST1HJgL1E4hbEx3w0G1Iwg7dik1R+0IleJYRSRJjoeIimuQuk3tCMKOSRGxJXI8RFjAKeMiPXztY8ZVYX0upUp3lu1Iv6h2AmGjhvnIUF9RPaQlYktyUtVOIGzUHYV71I4g7NSlNCkitiM3Te0EwkZ5J+7C1yCDMkTVi5fRWTYkz/bPDhXq0JjyGF33vNoxhB3KyC1UO0KlOFYRkZaIqIQoZxnqK6peToGJQpNZ7RgWkyIiRDk1SpcrYorqYcutEQcrItKdJSynT4vhbh/5ICKqnhQRWyEtEVFJD/ueUDuCsEPpubY7aMNxikhBLphse6Izob5Opr1qRxB2KDNPWiLWT0ZmiSrge2UHbk4mtWMIOyPdWbZAurJEFdAUZDOq7gW1Ywg7kyHdWTZAioioIve5HFY7grAzeYUyxNf65WepnUDYiWaZO9SOIOyM2Yavbug4RUSjUTuBsBPOKSdo65mpdgxhR8xmKSLWT+M4D1VUv1F+J9WOIOyIDdcQnNQOUGOkiNg0s0ZLgVZPoZOBAp0TBU4GCnUGCrQ6CnR6CrV6CnQ6CrVORcu0Ogr//l6g1Rb9rtFSoNFQoNVSqNFQoNFSABRoNBRq+PtnKAQKUIq/FyhmCv/+XoCZQkXhkQOXWHl4l7pPirAbnh3HAw3UjmERKSIOqEDrVPRmrNUXvQFffWPW6a+9CV/9Wact+q7RXntj1mgp0Gr+flO++oasKflmDMU/F70ZmylQlKI3Y8zXvTGbKFTMFCgmCswmChUTBUohBebCop/NhRSYCzArNzvwaAby/v4q46ZqOF7ppRip+1scSroMGxdVwzUnQ+0IFnOgIqKr8k0qaMjXGYrfhAt1Bgp0+r9/1lOgdSr6+WafjjXav9+Ur346vv6TsYaCq2/CGk3RJ+LrPh0XfzK+7s24QDH//YZcWPz9xjdjk9mEws3azlff/m9w9Y1YTo8AYNKl5ijp0goRVUejq/r3p5riMEUk3uDC/Hb9KNAoJT4dF0KJbooCxfT3z+Zrn5LNhUVvzObrPiWbCzEpN3tXrflPx6Lm3LkpUe0Iwt7YcE+JwxSRdIOB71IPqB1D2Lgh6c3gjJwnIqqWRme7RcR2k1eQUWdUO4KwAwP32G63g7BeWldXtSNYzGGKiEFnUDuCsHHh+f4Ytx9SO4awQ1oPT7UjWMxhioi0RERlTTwRBGY5oCWqns7TQ+0IFnOYIuLs5Kx2BGHDvMxGAqOPqR1D2CmthxQRq+fi5CKtEWGxxy61QMmw3bH8wrrppIjYBl8XX7UjCBukUaDDxni1Ywg7pvWUYyI2obZLbbUjCBs0NK05Ssx5tWMIO6UxGNA62253uxQRIW6j3x6ZAVpUH1tuhYAUESFuqV1+AM47ZFivqD62fDwEHKyIyDERUVHjj9UFG75gkLB+Tn5+akeoFIcqItISERXhY3ah7vojascQdk4fFKR2hEpxrCJilCIiyu/xi81RMuWyyqJ6SRGxIX6utt1sFDVHo0DbDZfUjiEcgBQRGyLdWaK8hqc1R4m9qHYM4QD0QYFqR6gUhyoivi6+OGkcZvZ7UQn37ZKD6aJmGKQlYjv0Wj3BnsFqxxBW7o68QAy75IC6qAE6HU516qidolIcqogANPJupHYEYeXGHvOXYb2iRujr1EHjZNu9I1JEhLhObbMbddYfVTuGcBC2flAdHLGIeEkRETf3+PmmKFkyrFfUDEPDhmpHqDTHKyLSEhE3oUND+AYZkSVqjrFFc7UjVJrDFZEGng1khJYo04iUFigX5NwQUXOMzaWI2By9Tk99z/pqxxBWKGpnodoRhCPRanFu1kztFJXmcEUE5LiIKO2uvCD0u2VYr6g5hpAQtC4uaseoNMcsInJcRNxg7BGZEkfULHs4HgIOWkQa+zRWO4KwIv5mN2qvP6x2DOFgnJu3UDtClXDIItLWr63aEYQVeTy2KUpOjtoxhIORlogNq+tWl0A32570TFQNHRparpfrp4uaZ2whLRGb1qFOB7UjCCswKrkFyqV4tWMIB6OvVw+n2vYxq7gUEeHQeu0oUDuCcECud3VUO0KVkSIiHFZEbn2c9so8WaLmuXWUImLzGng1wNfoq3YMoaJRh2upHUE4KNe77lI7QpVx2CIC0L5Oe7UjCJUEmDzw3SjDekXN04cEo69bV+0YVcahi4h0aTmux2KboOTkqh1DOCB76soCBy8id9S5Q+0IQgVOipYW0TFqxxAOyrWj/XRlgYMXkSY+TfAweKgdQ9SwcUlhKPGX1Y4hHJQ9jcwCBy8iWo2WiMAItWOIGtZth5ydLtRhCA1F7++vdowq5dBFBKB7cHe1I4gaFJkTgm7/cbVjCAflfu+9akeocg5fRLrU64JBa1A7hqghIw57qx1BODCPnj3VjlDlHL6IuOnduCvAvg50ibIFmTzx2XBI7RjCQen8auPSrq3aMaqcwxcRgB4hPdSOIGrA4+cao+TlqR1DOCiP7t3RaDRqx6hycrFx4N7696LT6DApJrWjWCTreBZXVl4h51wOhamFBD8RjGcHz+LbTbkmEpYkkL4nHVOmCYOfAd8evtTqdvMztpOjk0ndkkruhaJzKVwauFDngTq4NnQtXufKqiskrkwEwO8+P2r3uTahXPbpbC797xKNXm2ERqf+C8eg6GgafRZF7SDCYXn0sL+uLJCWCAC1jLVo699W7RgWM+eZMQYbCRxV9vT28YviyTyYSb1J9WjyThN8e/ly6dtLpO9Nv+k2s45l4XWXF6H/DKXRy43Q19IT80EMBSlFExbmns8lYVkC9R+rT/3H6pPwUwK554sKjmJSuLTgEoFjAq2igACMuxKGkpCodgzhoLReXrjZ2dDeq6SI/M2WR2l5tPagzpA6JVof18s+lY13hDfuLdwx+BmodW8tjPWN5Jy5+VDX+o/Wx7e7Ly4hLjgHOhM0PggUyDySCUBeXB7Gekbcw9xxD3PHWN9IXlxRV9GVVVdwa+ZWotWitnu3Z6kdQTgwj3sj0ej1aseoFlJE/mbLReR2XBu7krEvg4KUAhRFIfNoJvkJ+bi3ci/3Nsx5ZhSTgs5NB4BzPWfyE/LJT8on/0o+efF5ONdzJu9yHikbU/AfbD1j4btlN0B38ITaMYQDc+9hv8dd5ZjI3wLdA2lRqwVHk+1vavCAkQFcmn+J488cBx1oNBoCxwXi1syt3NtIWJKAk7cT7mFFhccYaKTOkDrEfBADQN0H6mIMNHL232epO7QumYcyufzzZTQ6DQEjAiq0r6o2/FDZLTQhaoLWzQ33Ll3UjlFtpIhcp1/DfnZZRJL/SCb7dDbBTwVjqG0g63gWcd/EoffW497y9q2RxBWJpG1PI/TFULSGa43XWt1qlTg4n7IpBa1Ri2tjV068eIJGrzWiIKWA81+cp+kHTdHqa77hG1LojffGQ3JAXajG874+aI1GtWNUG+nOus7AxgPt7sRDc76ZhKUJBDwUgGc7T4z1jfj28MWroxdXVl257f2vrLpC4m+JNHiuAcb6N38hFGYUcvmXywSODCT7TDbOdZ1xruuMewt3FJNCfnx+VT6scns0piFKvjr7FgLA+4EH1I5QraSIXMfL2cvuzhlRTAqKSSn9l9aCotz683niykQu/3qZBv/XAJdQl1uuG7cwjtq9aqOvpQdz0X5LZDDXfFvAWdHROPpMje9XiKucmzTGpU0btWNUKykiN3igqe19ajDlmsg5l0POuaLRVvlX8sk5l0N+Uj46Fx2uzVyJ/z6+6IB6Yj4pG1NI3ZxaYjTXhTkXiF8SX/x74m+JXP7pMkHjg9DX1lOQWkBBagGm3NLn0mQeKjpQX6t7UdeWS6gLeXF5ZBzIIDk6GY1Wg3OAczU/C6VNSGyJknj71pYQ1cVryBC1I1Q7OSZygzvr3kkDzwbEpMeoHaXccs7mEPN+TPHv8YuKioF3hDf1HqlXdB7H0gQuzL6AKcuE3ldPnSF1qNX12vGM/KR8uO6UjuS/klEKFc5/dr7EvvwG+lHn/jrFv5vzzVz69hL1H6uPRlu0AX0tPQEjA7j41UU0eg31JtYrcSylpvxjW0aN71OIqzR6PV4DB6odo9pplNv1aTig+Yfm8+HuD9WOISqhV1ZDJv5HhvUK9Xj07k29mR+rHaPaSXdWGQY2Hohea58nBjmKYQfUG1IsBNj/AfWrpIiUwcfoY9cnH9q7hoU+eGyW2XqFepwCA3C7u7PaMWqEFJGbsMUD7KLI5DOhUFCgdgzhwGo9/DAarWO8vTrGo7RAx7odCfEMUTuGqCCj4kSj9afUjiEcmNbDA++HHlI7Ro2RInITGo2GMS3HqB1DVNAjiWGYrySrHUM4MJ9hQ9G5l39eOlsnReQWBjUaRB3XOrdfUViNe7akqR1BODCNXo/P6NFqx6hRUkRuQa/TM67VOLVjiHLqk9UQzdHTascQDsxzQH/0/tYzg3VNkCJyG0OaDKGW8eZXABTW48H91nP9EuGANBp8J0xQO0WNkyJyG0YnI6PDHKt5aouaFPjiLsN6hYrcu3XDuWFDtWPUOCki5fBQ84fwcvZSO4a4hUlnQqCwUO0YwoH5TnS8VghIESkXN70bI5qPUDuGuAlXs54G0SfVjiEcmOudd+Larp3aMVQhRaScHm7xMG56mUrDGk26HIaSnKJ2DOHA/J55Ru0IqpEiUk5ezl4MazZM7RiiDJ23SAER6nGPjMS1vWO2QkCmgq+QsS3HsuT4EjIKZIpxa9E/szGa48fUjlHtFqeksDg1lYuFRdO5NDYYeMy3Nv/4+6S2H1JT+S09jSN5eWSZzWxr3ARPne6W2/z0SiKfJyWVWBZqMPBb6LWDw+9fTmBZWhquWi3P+PnR3/PascHVGen8mpbG5/XqV9XDtD0aDX7PPK12ClVJEakAH6MPk9tMZsauGWpHEX8bvK/mL3alhjp6J57x8yPEUHT55p/T0ph68QI/NgilibMzuWYz97i5c4+bOx9fSSz3dhsbDPy3fnDx79e/IazLzGBFejpf1a/PufwCXo6P4x5XN3ycnMgwmZiVmFjivo7Is29fjM2bqx1DVdKdVUEPt3iYBp4N1I4hgGYFtXHbeljtGDWiq7sHke7uNDAYaGAw8LSfH65aLQdyiq5mObpWLR7x9aWNi7FC29VpNPg5ORV/+ThdKyNn8vLp6OpKK6MLfT09cddqufD3xJYzEhN5yNuHQL3jXjJBYzDg7+CtEJAiUmF6rZ7n7nhO7RgCmHQ62CGH9ZoUhZXp6eQoCm1cXCq1rdj8fCJPnaLXmdM8f+kSl66b/biZ0ZlDubmkmUwczs0lV1EINhjYnZ3N0bxcRvr4VPah2DSfkSPRBwWpHUN10p1lgcj6kdwdeDdbLm1RO4rDclcMBK87jiNdlvNEXi7Dz50jX1Fw1Wr5T2AQjZ0t785rbXTh7YAAQvUGEk2FfH4liVGx5/g1NBQ3rY573Nzp75nD0HMxGDVa3q0bgItWyxsJCbwTEMDi1FS+S0nBR6fj9bp1aVKJLLZG5+VF7Ucnqx3DKkhLxEIv3PkCThqpwWqZHB+GkupYky02MDjzU4NQFoc0YJi3N/+Kj+NUXp7F2/uHuzu9PTxpZjRyj5s7X9arR4bZzOr0awNHptb2Y03DRvwSGkoPDw/mJiXR2c0VJ+DLpCt8GxzMEG8vpsVdqoJHaDtqP/EEOk9PtWNYBSkiFmrk3YgHmz2odgyHddfmK2pHqHEGjYYQg4GWRiPP+vnTzNmZb1Kqbnizp05HA4OBcwX5Zd5+Ji+P5elpPFHbjx052dzh6kotJyd6e3j+PSrMVGVZrJmxVSt8Hh6udgyrIUWkEqa0nSLToahgUEYTOBmjdgzVKUCBYq6y7WWZzcTm5+PnVLqFrSgKryfE809/f9y0WswKFCpFnYlXv5scoW9Rp6Pu9Ncd5qqF5SHPRCV4OXvxWJvH1I7hcO7fa1A7Qo37KPEyu7KzuViQz4m8XD5KvMyO7Gz6/X3eRmJhIUdzc4nNLzowfiIvj6O5uaSarrUOxp2P5bvrWi7/vnyZnX9vc29ONk9evIBOo6GvR+lumqVpadTSOdHV3QOAdi4ubM/OZn9ODgtSkmlkMNz2vBR7UGvkCFxatlQ7hlWRTv1KGtZsGD+d/IkTKSfUjuIQWub747LN8WbrTTaZeDHuEokmEx5aLU2dnZlbrz53uxVNxfN9akqJEwdHn48F4O26dbnfyxuA8/n5pJiujWZLKCzguUuXSDWbqKXT0d7FhUXBIdS6oSVypbCQ2UlXWBhy7XLRrV1cGOtTi0cvnMfXyYl36gZU10O3Gk516+L35JNqx7A6GkVRHKERWq0OJx1mxG8jMCmO0Sespo+PtCPol51qxxAOKOiT/+DZs6faMayOdGdVgZa+LeV67DXASzFSb91xtWMIB+TetasUkJuQIlJFHm/7OKFeoWrHsGuTLjVHSU9XO4ZwMBpXV+q+8rLaMayWFJEq4qxz5o2730Crkae0uty5qfxzQglRVfz/71n0gYFqx7Ba8o5Xhdr6t5VurWryQHozOHNO7RjCwbhHRlJrhFyQ7lakiFSxJ9o+QVOfpmrHsDsD9si/qqhZutq1CXjnbbVjWD2rfGVGR0ej0WhITU1VO0qF6XV63rnnHfRax53dtKqF5/tj3O4Ys/UK6xH4zts4+fqqHcPqVaiIfPHFF7Ru3RpPT088PT3p3Lkzq1atqtAOY2Ji0Gg07Nu3r3hZRkYGXbt2JSwsjAsXLlRoe9aoWa1mTG03Ve0YdmPiiSAwV92Z2ULcjs+IEbj/4x9qx7AJFSoi9erV47333mP37t3s2rWLbt26MXDgQA4ftvxTYmJiIl27diUrK4uNGzdSr149i7dlTca2HEungE5qx7B5XmYjgdH2f+VCYT2cmzTG/4Xn1Y5hMypURPr37899991HkyZNaNq0KW+//Tbu7u5s27bNop2fP3+eLl264OXlxV9//YXvTZqOSUlJDB8+nKCgIFxdXQkPD2fRokUl1lm6dCnh4eG4uLjg6+tLjx49yMrKAoq6xzp27Iibmxve3t5ERERw7ty1g7S//PIL7du3x2g00rBhQ6ZPn05hJa9TodVo+fc//k2Am/2fyVudHo9rgZIhlyMWNUNjMBA4YwZaB5rWvrIsPiZiMplYvHgxWVlZdO7cucL3P378OBEREYSFhbFy5Urc/75WdFlyc3Pp0KEDv/32G4cOHWLSpEmMGjWKHTt2ABAXF8fw4cMZP348R48eJTo6msGDB6MoCoWFhQwaNIjIyEgOHDjA1q1bmTRpEhqNBoCNGzcyevRonnrqKY4cOcLs2bOZP38+b79d+QNqPkYfPr73Ywxax5vrqSpoFGi/IV7tGMKB+D/3HMZmzdSOYVMqPO3JwYMH6dy5M7m5ubi7u7Nw4ULuu+++ct8/JiaG0NBQDAYDERERrF27Ft0NE7dFR0fTtWtXUlJS8Pb2LnM7/fr1o3nz5syYMYM9e/bQoUMHYmJiCLlufh+A5ORkfH19iY6OJjIystR2evToQffu3Zk2bVrxsm+//ZYXXniBS5eq5hoJP574kde3vl4l23Ikw1KbM+QLx5snS6jDa+AAAt9/X+0YNqfCLZFmzZqxb98+tm/fzmOPPcaYMWM4cuRIhXc8YMAANm7cyE8//XTbdU0mE2+++Sbh4eHUqlULd3d31qxZQ2xs0SRzbdq0oXv37oSHh/Pggw8yd+5cUv6erbRWrVqMHTuWqKgo+vfvz6xZs4iLiyve9v79+3njjTdwd3cv/nrkkUeIi4sjOzu7wo+rLEOaDmFwk8FVsi1H0m+PRu0IwkEYW7Wi7htvqB3DJlV6AsYePXrQqFEjZs+eXa71r7ZE9u7dy/Lly3njjTf47rvvGDp0aPE6N7ZE3nvvPWbMmMHMmTMJDw/Hzc2Np59+GicnJ37++Weg6HoHW7Zs4ffff2fZsmXEx8ezfft2QkOLpiLZu3cvq1evZvny5Rw8eJC1a9fSqVMnXFxcmD59OoMHl36Tb9iwIdoqum5Avimf0atGczhJhqqWR7v8AKZ9dAFkflBRzXS1axO6dAn6unXVjmKTKj0VvNlsJs/CS3S+8soraLVaRowYgaIoDBs2rMz1Nm/ezMCBAxk5cmTxPk+cOEFYWFjxOhqNhoiICCIiInj11VcJCQlh2bJlPPvsswC0a9eOdu3aMW3aNDp37szChQvp1KkT7du35/jx4zRu3Niix1BeBp2Bj+/9mKErhpKal1qt+7IH44/VBeW82jGEvdPrqTdrphSQSqhQEZk2bRp9+vQhODiYjIwMFi5cSHR0NGvWrCleZ/To0QQFBfHuu++Wa5svvfQSOp2OESNGYDabGT689GUnmzRpwtKlS9myZQs+Pj589NFHJCQkFBeR7du38+eff9KrVy/8/f3Zvn07iYmJtGjRgrNnzzJnzhwGDBhAYGAgx48f5+TJk4wePRqAV199lX79+hEcHMwDDzyAVqtl//79HDp0iLfeeqsiT89tBbgH8P4/3uexPx7DXIVXpLM3vmZX6q4/grRBRHWr+9JLuHbooHYMm1ahInL58mVGjx5NXFwcXl5etG7dmjVr1tDzuimSY2NjK9wF9OKLL6LVahk1ahSKohB4w2RnL7/8MmfOnCEqKgpXV1cmTZrEoEGDSEtLA8DT05MNGzYwc+ZM0tPTCQkJ4cMPP6RPnz4kJCRw7NgxFixYQFJSEgEBAUyZMoXJkycDEBUVxYoVK3jjjTd4//330ev1NG/enIkTJ1boMZTX3YF381T7p/h498fVsn178OjFZiiZcs0QUb28hw3D56Gyez9E+clFqVTy7vZ3WXhsodoxrI5GgR8W1kGJvah2FGHHXO+4g+B5X6PRy/RElWWVc2c5ghc7vkjvBr3VjmF1hqc1lwIiqpVz06bU+/wzKSBVRIqISjQaDe/c845MjXKD+3ZJw1hUH329etT/ai46T0+1o9gNKSIq0uv0zOw6kzDfsNuv7ADuyAvEsKvi5xwJUR46X1+C//sVen9/taPYFSkiKnPTu/F5988J9ghWO4rqxh2rI+eFiGqhdXcneO4cDDfMaCEqT4qIFfB18WV2z9nUdqmtdhTV1Da74R8tJ2KKqqcxGKj36acYw6TFXx2kiFiJeh71+LLHl7jrbz4RpT17/HxTlCqaZkaIYjodgTM+wK3TXWonsVtSRKxIs1rN+LT7p7g6uaodpUbp0BC+QUZkiSqm1RLwxht49uqldhK7JkXEynSo04E5vebgYfBQO0qNGZHSAuVC1cyYLARQ1AJ5/z28h8jEp9VNiogVauPXhv/2+i8+zj5qR6kRUTsrdwEwIUrQ6wn68EO8+vdXO4lDkCJipVr4tmBe73n4ufipHaVadcoNQr9bhvWKqqExGKj3n1l49o5SO4rDkCJixRp5N2J+7/l2fYndMUftu0iKmqMxGqn3+ed4dO2qdhSHIkXEygV7BrOg9wK7PI/E3+xG7fUyrFdUntbVlfpzZuN+T4TaURyOFBEbEOAewPze82nk1UjtKFXq8dimKDk5ascQNk7r6Un9/36FW8eOakdxSFJEbISfqx/zes+jpW9LtaNUCR0aWq6Xi06JytEHB9Ng8WJc27VTO4rDkiJiQ3yMPszvPZ+oBrZ/0HB0chjKpXi1Ywgb5tK+PQ2+X4xzw1C1ozg0KSI2xuhkZEbkDB5v+zgaNGrHsVjPHflqRxA2zLN/f4Lnz8PJxzGGwVszKSI26rE2j/HhvR/i4uSidpQKi8itj9Peo2rHEDaq9tSpBH3wb7QGg9pRBFJEbFrPkJ4s6L2Aum511Y5SIaMO11I7grBBGoOBwA8+wG/qFLWjiOtIEbFxLXxbsKjvIlr7tVY7SrkEmDzw3SjDekXF6GrXJnj+PLz691M7iriBFBE7UNulNvOi5tG/ofVP8/BYbBOUnFy1Ywgb4nrXXTRc9hOu7durHUWUQaMochUge/LNkW/4ePfHFJgL1I5SipOiZdF8b5T4y2pHEbZAq6X2o49Se+oUNFr5vGut5C9jZ0aFjWJh34U09GqodpRSxiWFSQER5aLz9SX4q7n4PfmEFBArJ38dO9S8VnO+7/c9Q5sOVTtKCd12yNnp4vZcO3YkdNlPuN19t9pRRDlId5ad+yv2L17b8hqpeamq5ojMCWHKzNOqZhBWTqvFd/Ik/KZORaPTqZ1GlJO0ROxct+Bu/DTgJzoFdFI1x4jD3qruX1g3fVAQwV9/jf9TT0kBsTHSEnEQiqKw4PAC/rP3PzV+0L1eoRcf/ycTJS+vRvcrbIP3sGHUeeF5tG5uakcRFpAi4mCOJh3l1S2vciz5WI3t8+3T7Wnyw44a25+wDU6BAQS8+SbuETJ9uy2TIuKATGYTi44t4tN9n5JVkFWt+zIoOr6b54mSkFit+xE2RKvF5+GH8X/maWl92AEpIg7scvZl/r3z36yJWVNt+5icGE73r/ZW2/aFbTE0bkTAm2/K1O12RIqIYMvFLby9/W1iM2KrfNuLVjREd/BElW9X2Batmxu+j07Gd8wYNDJxol2RIiIAyDfl89+D/+Wrg1+Rb66aadq7ZTfg0VmnqmRbwkZptXgNvh//p5/GqXZttdOIaiBFRJQQmx7L29vfZsulLZXe1twdrfH6c08VpBK2yPWOO6jzr2kYw8LUjiKqkRQRUaZNFzfx6d5POZxk2Yy7IYXezJiVjpIvF59yNPqgIPyffx7P3rZ/BU5xe3KyoSjTPUH3sLjfYmbeO5PG3o0rfP9HYxpKAXEwWg8P/J55hoarVtpkAYmOjkaj0ZCamqp2FJsiRUTcUveQ7vw44Efe6/IewR7B5bqPs6KjcfSZak4mrIXWy4vaU6fS+M8/qD15UrVecfC9995Do9Hw9NNPV+h+MTExaDQa9u3bV7wsIyODrl27EhYWxoULF6o2qANxUjuAsH5ajZa+DfsS1SCKX079wuwDs4nLirvp+hMSW6IkyrEQe6fz9qbW2DH4jByJzt292ve3c+dOZs+eTevWlb8AW2JiIn369EGr1bJx40Z8fX05dUoGgVhCWiKi3Jy0TgxpOoTf7v+NFzu+iJ+LX5nr/WNbRg0nEzVJ5+OD37PPFrU8Hn20RgpIZmYmI0aMYO7cufj4+FRqW+fPn6dLly54eXnx119/4evrW+Z6SUlJDB8+nKCgIFxdXQkPD2fRokUl1lm6dCnh4eG4uLjg6+tLjx49yMoqOoE3Ojqajh074ubmhre3NxEREZw7d674vr/88gvt27fHaDTSsGFDpk+fTmFhYaUemxqkiIgK0+v0jGgxgjVD1vBWxFs082lWfFtUdkO0h0+qmE5UFyc/P/yff76oeEx6pEbPNp8yZQp9+/alR48eldrO8ePHiYiIICwsjJUrV+J+iwKYm5tLhw4d+O233zh06BCTJk1i1KhR7NhRNIVPXFwcw4cPZ/z48Rw9epTo6GgGDx6MoigUFhYyaNAgIiMjOXDgAFu3bmXSpEloNBoANm7cyOjRo3nqqac4cuQIs2fPZv78+bz99tuVenxqkNFZokpsi9vG/w7/j7E/puGxTrqy7InrHXfgM+JhPHr0QKPX1/j+Fy9ezNtvv83OnTsxGo3ce++9tG3blpkzZ5Z7GzExMYSGhmIwGIiIiGDt2rXobpgtODo6mq5du5KSkoK3t3eZ2+nXrx/NmzdnxowZ7Nmzhw4dOhATE0NISEiJ9ZKTk/H19SU6OprIyMhS2+nRowfdu3dn2rRpxcu+/fZbXnjhBS5dulTux2UN5JiIqBKdAjrRKaAT+Y1jSAleROqynzGnp6sdS1hI4+qKV//++Dz8MMZmTVXLcf78eZ566inWrl2L0Wis9PYGDBjAzz//zE8//cSDDz54y3VNJhPvvPMOP/zwAxcvXiQ/P5+8vDxcXV0BaNOmDd27dyc8PJyoqCh69erFAw88gI+PD7Vq1WLs2LFERUXRs2dPevTowdChQwkICABg//79bN68uUTLw2QykZubS3Z2dvE+bIG0RES1MOfkkLZ8OamLvyf3yBG144hyMjRogM/Dw/G6/350Hh5qx+Hnn3/m/vvvL9FqMJlMaDQatFoteXl5pVoUZbnaEtm7dy/Lly/njTfe4LvvvmPo0GtX/7yxJfLee+8xY8YMZs6cSXh4OG5ubjz99NM4OTnx888/A0WXWNiyZQu///47y5YtIz4+nu3btxMaGgrA3r17Wb16NcuXL+fgwYOsXbuWTp064eLiwvTp0xk8eHCprA0bNkRrQ5cElpaIqBZaFxd8hg7FZ+hQ8k6eJG35CtJXrKDAxprqjkDr4YFHz5549e+Ha6dOxf321qB79+4cPHiwxLJx48bRvHlz/vnPf5argNzolVdeQavVMmLECBRFYdiwYWWut3nzZgYOHMjIkSMBMJvNnDhxgrDrzsDXaDREREQQERHBq6++SkhICMuWLePZZ58FoF27drRr145p06bRuXNnFi5cSKdOnWjfvj3Hjx+nceOKn4NlbaSIiGrn3KQJ/s8+g98zT5Ozaxdpvy4nfc0a6e5SkcZoxP3ee/Hsex/ukZHVem5HZXh4eNCqVasSy9zc3PD19S2xfPTo0QQFBfHuu++Wa7svvfQSOp2OESNGYDabGT58eKl1mjRpwtKlS9myZQs+Pj589NFHJCQkFBeR7du38+eff9KrVy/8/f3Zvn07iYmJtGjRgrNnzzJnzhwGDBhAYGAgx48f5+TJk4wePRqAV199lX79+hEcHMwDDzyAVqtl//79HDp0iLfeesvSp0sVUkREjdFoNLjeeSeud95JnVdeJnP9etJ/XU7mxo0oublqx7N/Tk64RdyNV9++uHfrjs7dfq7lERsbW+EuoBdffBGtVsuoUaNQFIXAwMASt7/88sucOXOGqKgoXF1dmTRpEoMGDSItLQ0AT09PNmzYwMyZM0lPTyckJIQPP/yQPn36kJCQwLFjx1iwYAFJSUkEBAQwZcoUJk+eDEBUVBQrVqzgjTfe4P3330ev19O8eXMmTpxYNU9IDZJjIkJ15txcsrZtI2vDBjLXb6Dg4kW1I9kNnZcXrnd3xv2eLrh364pTJc+xEOJGUkSE1ck7dYrM9RvI3LCB7D17oKBmrwlv07RajOGtiopGl3swhoejseC4gRDlJUVEWDVTZiZZW7aQvXMXOfv2kXvsmBSVG+iDg3Ht0AH3Lvfgdvfd6G5yjoMQ1UGKiLAp5txccg8dInvvXnL27Sdn3z5MSUlqx6oxWi8vXMLDcWndGpc2rTG2bi1dVEJVUkSEzcuPjSVn/37yTpwg7/QZ8k+fJv/CBTCZ1I5WKTq/2jiHNMC5aROMrVvj0qYNhgYNrGoIrhBSRIRdMufnkx8TQ/6ZM+SdOk3+mdPknTlLYXw8Jiu6XoTGxQVDgwYYGoTgHBqKITS06PfQ0BqZ2FCIypIiIhyOOT8fU2IihYmJFPz9/fovc1YWSm4e5tycou95uSi5eSi5uSg3Ho/RatHo9WgMhqKv4p/1aN3c0Hl74+Ttg87HB12tWjjVro2Tvz9Ofn44+fuh8/aWloWwaVJEhKgAxWQqOqdFoykqFk5yqpVwbFJEhBBCWMx2ZvkSQghhdaSICCGEsJgUESGEEBaTIiKEEMJiUkSEEEJYTIqIEEIIi0kREUIIYTEpIkIIISwmRUQIIYTFpIgIIYSwmBQRIYQQFpMiIoQQwmJSRIQQQlhMiogQQgiLSRERQghhMSkiQgghLCZFRAghhMWkiAghhLCYFBEhhBAWkyIihBDCYlJEhBBCWEyKiBBCCItJERFCCGExKSJCCCEsJkVECCGExaSICCGEsJgUESGEEBaTIiKEEMJiUkSEEEJYTIqIEEIIi0kREUIIYTEpIkIIISwmRUQIIYTFpIgIIYSwmBQRIYQQFpMiIoQQwmJSRIQQQlhMiogQQgiLSRERQghhMSkiQgghLCZFRAghhMWkiAghhLCYFBEhhBAWkyIihBDCYlJEhBBCWOz/AcmtnkbrvculAAAAAElFTkSuQmCC",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.pie(school.values(), labels=school.keys(), autopct='%1.1f%%') # Setzen von Prozentwerten\n",
|
||
"\n",
|
||
"plt.title(\"Klassenverteilung einer Grundschule\")\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a0a13fc0-3ae1-4ab5-a488-8c5247cf74c5",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-430a11a7f58f4fa5",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Pie Charts besitzen außerdem den Parameter `shadow`. \n",
|
||
"\n",
|
||
"Standardmäßig ist dieser auf `False` gesetzt. Wird der Wert auf `True` geändert, erscheint das Pie Chart mit einem **Schatten**, was die Darstellung plastischer wirken lässt."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 55,
|
||
"id": "62971d68-8cdd-48c4-8f60-209bffe64e84",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-408e63a1464d64ea",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZEAAAGbCAYAAAAFuq0xAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAbzBJREFUeJzt3Xd4VGX68PHvzGRKeg+QQgihBoJAFMHAAhIISBFEQaSIlV1x1d3XVVldXSyrrq6rq65r+YnuKjYUuyIqSO+EIh0SAqSQ3jPtnPePQCAkQDIkOZnJ/bmuuZKceeac+0xm5p6nnOfRqaqqIoQQQrhAr3UAQggh3JckESGEEC6TJCKEEMJlkkSEEEK4TJKIEEIIl0kSEUII4TJJIkIIIVwmSUQIIYTLJIkIIYRwmSQR4K9//Ss6nU7rMNq1ESNGMGLEiNq/MzIy0Ol0vPPOO5rF1JzkNda83nnnHXQ6HRkZGc2+b51Ox913392s++zSpQtz585t1n22FR6bRE6/yLZs2VJne0lJCYMGDcJisfD9999rFJ1n+fbbb/nrX/+qdRjCRVarlZdffpmhQ4cSHByMyWQiMjKSSZMm8cEHH+B0OrUOUbRhHptEGlJaWsqYMWPYuXMnS5cuZezYsVqH5BG+/fZbFi5ceEn7+OGHH/jhhx+aKaK255FHHqGqqkrrMOrJy8sjOTmZe+65Bz8/Px555BFef/11fv/731NRUcFNN93E3/72N63DFG2Yl9YBtJaysjJSU1NJS0vjs88+Y9y4cVqH5PYqKirw9fVtln2ZTKZm2U9b5eXlhZdX67/dqqurMZlM6PUNf1+cPXs227dv59NPP+W6666rc9+CBQvYsmUL+/fvv6RjCM/WLv7r5eXljB07lm3btvHpp58yfvz4iz5m0aJFXH311URERGA2m0lISOC1116rV27Lli2kpqYSFhaGt7c3cXFx3HrrrXXKfPjhhyQlJeHv709AQACJiYm89NJLdcoUFxdz3333ERMTg9lsplu3bjz77LMoilJb5nQ/wfPPP88bb7xBfHw8ZrOZK664gs2bN9eWe/7559HpdBw9erRevAsWLMBkMlFUVFS7bePGjYwdO5bAwEB8fHwYPnw4a9eurfO40236e/bs4aabbiI4OJihQ4cyd+5cXn31VaCmLfn07TRFUXjxxRfp06cPFouFDh06MG/evDrHh/p9Ig05X5m5c+fSpUuXJj9Pp33yySckJCRgsVjo27cvS5curbfPC/nuu+8YNmwYvr6++Pv7M378eH799dc6ZRrqEznd9v7555/Tt29fzGYzffr0abCZ9cSJE9x666106NChttzbb79dp8zKlSvR6XR8+OGHPPLII0RFReHj40NpaWmDca9fv55ly5Zx55131ksgp11++eXMnDmzUcc4X79PQ/0XXbp0YcKECaxZs6a2eblr167897//rff4X3/9lauvvhpvb2+io6N58skn67wvTmvMe1FRFF566SUSExOxWCyEh4czduzYes3ewEX/L+d7jTS2/6sx73l34PE1kYqKCsaNG8fmzZtZsmQJEyZMaNTjXnvtNfr06cOkSZPw8vLiq6++4q677kJRFObPnw/AyZMnGTNmDOHh4Tz00EMEBQWRkZHBZ599Vruf5cuXM2PGDEaNGsWzzz4LwN69e1m7di333nsvAJWVlQwfPpwTJ04wb948OnfuzLp161iwYAHZ2dm8+OKLdWJbvHgxZWVlzJs3D51Ox9///neuu+46jhw5gtFoZNq0aTzwwAN8/PHH/OlPf6rz2I8//pgxY8YQHBwMwM8//8y4ceNISkriscceQ6/X1ybQ1atXM2jQoDqPv+GGG+jevTt/+9vfUFWVAQMGkJWVxfLly/nf//5X73mcN28e77zzDrfccgv33HMP6enpvPLKK2zfvp21a9diNBob9f9wxcWeJ4BvvvmG6dOnk5iYyNNPP01RURG33XYbUVFRjTrG//73P26++WZSU1N59tlnqays5LXXXmPo0KFs3779oolozZo1fPbZZ9x11134+/vzr3/9i6lTp5KZmUloaCgAubm5DB48uDbphIeH891333HbbbdRWlrKfffdV2efTzzxBCaTifvvvx+r1XreWt5XX30FwKxZsxp1rq4c40IOHTrE9ddfz2233cbNN9/M22+/zdy5c0lKSqJPnz4A5OTkMHLkSBwOBw899BC+vr688cYbeHt719lXY96LALfddhvvvPMO48aN4/bbb8fhcLB69Wo2bNjA5ZdfXluuMf+XS9HU93ybpnqoRYsWqYAaGxurGo1G9fPPPz9v2ccee0w996morKysVy41NVXt2rVr7d9Lly5VAXXz5s3n3fe9996rBgQEqA6H47xlnnjiCdXX11c9cOBAne0PPfSQajAY1MzMTFVVVTU9PV0F1NDQULWwsLC23BdffKEC6ldffVW7bciQIWpSUlKd/W3atEkF1P/+97+qqqqqoihq9+7d1dTUVFVRlDrnHhcXp44ePbp22+nnaMaMGfXinz9/fr3nT1VVdfXq1Sqgvv/++3W2f//99/W2Dx8+XB0+fHjt36fPddGiRectc9rNN9+sxsbG1ntsY56nxMRENTo6Wi0rK6vdtnLlytrXzoWUlZWpQUFB6h133FFne05OjhoYGFhne0OvMUA1mUzqoUOHarft2LFDBdSXX365dtttt92mdurUSc3Pz6/z+BtvvFENDAysfa2uWLFCBdSuXbs2+Po915QpU1RALS4urrO9qqpKzcvLq70VFRXV3nehYzR0jqp65r2Ynp5euy02NlYF1FWrVtVuO3nypGo2m9X/9//+X+22++67TwXUjRs31ikXGBhYZ5+NeS/+/PPPKqDec8899e47+/Xf2P/Lua+7Cz0PsbGx6s0331z7d2Pf8+7A45uzcnNzsVgsxMTENOlxZ3/TKSkpIT8/n+HDh3PkyBFKSkoACAoKAuDrr7/Gbrc3uJ+goCAqKipYvnz5eY/1ySefMGzYMIKDg8nPz6+9paSk4HQ6WbVqVZ3y06dPr61JAAwbNgyAI0eO1CmzdetWDh8+XLvto48+wmw2c+211wKQlpbGwYMHuemmmygoKKg9bkVFBaNGjWLVqlX1qta//e1vz3seDZ1XYGAgo0ePrnNeSUlJ+Pn5sWLFikbvyxUXe56ysrLYtWsXc+bMwc/Pr7bc8OHDSUxMvOj+ly9fTnFxMTNmzKhzfgaDgSuvvLJR55eSkkJ8fHzt3/369SMgIKA2RlVV+fTTT5k4cSKqqtY5TmpqKiUlJWzbtq3OPm+++eZ639QbcrqZ6+xzB/jPf/5DeHh47W3o0KH1HtvYY1xIQkJC7f8EIDw8nJ49e9Z5HX/77bcMHjy4To04PDy8ThMbNO69+Omnn6LT6Xjsscfq3Xdu89PF/i+Xqqnv+bbM45PI66+/jslkYuzYsRftIDzb2rVrSUlJwdfXl6CgIMLDw/nzn/8MUJtEhg8fztSpU1m4cCFhYWFce+21LFq0CKvVWrufu+66ix49ejBu3Diio6O59dZb67WtHjx4kO+//77OGzc8PJyUlBSgpqp+ts6dO9f5+/QH5dn9DDfccAN6vZ6PPvoIqPkw+uSTTxg3bhwBAQG1x4WaD4Rzj/3WW29htVprz/W0uLi4Rj+HBw8epKSkhIiIiHr7Ly8vr3deze1iz9PpPqNu3brVe2xD2851+vm7+uqr653fDz/80KjzOzfG03GejjEvL4/i4mLeeOONese45ZZbgPqvj8b+j/z9/YGaPsOzTZ06leXLl7N8+XL69evX4GOb8jo4n4udO9T8j7p3716vXM+ePev83Zj34uHDh4mMjCQkJKRZYrsUTX3Pt2Ue3yeSkJDAt99+y6hRoxg9ejRr1669aK3k8OHDjBo1il69evHCCy8QExODyWTi22+/5Z///Gftt3OdTseSJUvYsGEDX331FcuWLePWW2/lH//4Bxs2bMDPz4+IiAjS0tJYtmwZ3333Hd999x2LFi1izpw5vPvuu0BNZ9/o0aN54IEHGoynR48edf42GAwNllPPWuk4MjKSYcOG8fHHH/PnP/+ZDRs2kJmZWdsvc/q4AM899xz9+/dvcJ/nfkttyrdPRVGIiIjg/fffb/D+8PDwRu8Lap5vtYHVnM93HUNjnqdLcfr5+9///kfHjh3r3d+Y0VgXi/H0MWbNmsXNN9/cYNlzP+gb+z/q1asXALt37yY5Obl2e0xMTO175PQ35XM1dIzzdSa3xv+nMe/FpmhMbE0937M19T3flnl8EgEYNGgQn3/+OePHj2f06NGsXr36gh9gX331FVarlS+//LLON5LzNU8MHjyYwYMH89RTT7F48WJmzpzJhx9+yO233w7UDF+dOHEiEydORFEU7rrrLl5//XX+8pe/0K1bN+Lj4ykvL6/9FtJcpk+fzl133cX+/fv56KOP8PHxYeLEibX3n66uBwQEXNKxz/dmio+P58cffyQ5OfmSmz6g5gOtoeaEhkahNUZsbCxQ08F7roa2nev08xcREdHs/7vTwsPD8ff3x+l0NvsxJkyYwDPPPMP7779fJ4m46nRNr7i4uLZ5CVz//0DN/+h0je9s52tVuNB7MT4+nmXLllFYWNio2sjFBAcHU1xcXG97Y863pd7zWvD45qzTRo0axQcffMChQ4cYO3bseYc9wplvIWd/6ygpKWHRokV1yhUVFdX71nT6G/3panRBQUGd+/V6fe03x9Nlpk2bVjvc8lzFxcU4HI7GnGI9U6dOxWAw8MEHH/DJJ58wYcKEOtd1JCUlER8fz/PPP1+vSQNqmlIa4/Q+z31DTZs2DafTyRNPPFHvMQ6Ho8E34IXEx8ezb9++OnHt2LGj3nDkxoqMjKRv377897//rXP+v/zyC7t27bro41NTUwkICOBvf/tbg+3wjX3+LsRgMDB16lQ+/fRTdu/e3azHSE5OZvTo0bzxxht88cUXDZZpSq3gdFI9uz2/oqKitsbtimuuuYYNGzawadOm2m15eXn1areNeS9OnToVVVUbvDDWldpPfHw8JSUl7Ny5s3ZbdnY2S5cuvehjW+o9r4V2URM5bcqUKbz55pvceuutTJo0ie+//x6LxVKv3JgxY2prD/PmzaO8vJw333yTiIgIsrOza8u9++67/Pvf/2bKlCnEx8dTVlbGm2++SUBAANdccw0At99+O4WFhVx99dVER0dz9OhRXn75Zfr370/v3r0B+NOf/sSXX37JhAkTaoc4VlRUsGvXLpYsWUJGRgZhYWFNPt+IiAhGjhzJCy+8QFlZGdOnT69zv16v56233mLcuHH06dOHW265haioKE6cOMGKFSsICAioHQZ6IUlJSQDcc889pKamYjAYuPHGGxk+fDjz5s3j6aefJi0tjTFjxmA0Gjl48CCffPIJL730Etdff32jz+fWW2/lhRdeIDU1ldtuu42TJ0/yn//8hz59+lzwS8GF/O1vf+Paa68lOTmZW265haKiIl555RX69u3bYGI9W0BAAK+99hqzZ89m4MCB3HjjjYSHh5OZmck333xDcnIyr7zyiktxne2ZZ55hxYoVXHnlldxxxx0kJCRQWFjItm3b+PHHHyksLHR53++99x5jx45l8uTJjBs3jpSUFIKDg8nJyeHHH39k1apVjb4wd8yYMXTu3JnbbruNP/3pTxgMBt5+++3a58QVDzzwAP/73/8YO3Ys9957b+0Q39jY2Dof3o15L44cOZLZs2fzr3/9i4MHDzJ27FgURWH16tWMHDmyyfNl3XjjjTz44INMmTKFe+65p3Z4d48ePeoNdjhXS73nNaHBiLBWcXpYYUND/p5//nkVUCdMmKDa7fYGh+R9+eWXar9+/VSLxaJ26dJFffbZZ9W33367zrDCbdu2qTNmzFA7d+6sms1mNSIiQp0wYYK6ZcuW2v0sWbJEHTNmjBoREaGaTCa1c+fO6rx589Ts7Ow6xysrK1MXLFigduvWTTWZTGpYWJh61VVXqc8//7xqs9lUVT0zdPW5556rd06A+thjj9Xb/uabb6qA6u/vr1ZVVTX4XG3fvl297rrr1NDQUNVsNquxsbHqtGnT1J9++qm2zOnnKC8vr97jHQ6H+vvf/14NDw9XdTpdvefyjTfeUJOSklRvb2/V399fTUxMVB944AE1Kyurtkxjhviqqqq+9957ateuXVWTyaT2799fXbZs2XmH+Db2efrwww/VXr16qWazWe3bt6/65ZdfqlOnTlV79erV4PN1rhUrVqipqalqYGCgarFY1Pj4eHXu3Ll1XgfnG+I7f/78evs7dzioqqpqbm6uOn/+fDUmJkY1Go1qx44d1VGjRqlvvPFGnTgA9ZNPPmlU3KdVVVWpL774ojpkyBA1ICBA9fLyUjt27KhOmDBBff/99+sMT7/YMbZu3apeeeWVta/1F1544bxDfMePH1/v8Q0N4965c6c6fPhw1WKxqFFRUeoTTzyh/t///V+T34uqWvNafe6559RevXqpJpNJDQ8PV8eNG6du3bq1tkxT/i8//PCD2rdvX9VkMqk9e/ZU33vvvUYN8VXVxr3n3YFOVZupl1EID9K/f3/Cw8MvODRbCNGO+kSEaIjdbq/X/rxy5Up27Nhx0WlYhBAgNRHRrmVkZJCSksKsWbOIjIxk3759/Oc//yEwMJDdu3c3yxQXQniydtWxLsS5goODSUpK4q233iIvLw9fX1/Gjx/PM888IwlEiEaQmogQQgiXSZ+IEEIIl0kSEUII4TJJIkIIIVwmSUQIIYTLJIkIIYRwmSQRIYQQLpMkIoQQwmWSRIQQQrhMkogQQgiXSRIRQgjhMkkiQgghXCZJRAghhMskiQghhHCZJBEhhBAukyQihBDCZZJEhBBCuEySiBBCCJdJEhFCCOEySSJCCCFcJklECCGEyySJCCGEcJkkESGEEC6TJCKEEMJlkkSEEEK4TJKIEEIIl0kSEUII4TJJIkIIIVwmSUQIIYTLJIkIIYRwmSQRIYQQLpMkIoQQwmWSRIQQQrhMkogQQgiXSRIRQgjhMkkiQgghXCZJRAghhMskiQghhHCZJBEhhBAukyQihBDCZV5aByCE1qrtTk6WWjlZVk1JlZ0Km5Mqm4NKm/PU7dTvVic2p4JOBwadDi+DDr1Oh5deh15f89Og1+NrMhDkayLI20iQj5Egb1PNTx8j/haj1qcrRLOSJCI8Xk5JNYdOlpOeX052STW5pxJGbmnN7yVV9laLxUuvI8TXRHSwNzEhPsQE+xATcub3yCBvDHpdq8UjxKXSqaqqah2EEJdKUVSOFlZy6GT5mVteOUdOllNmdWgdXqN56XVEBnkTH+5Lr04B9OroT+9OAcSH+0lyEW2SJBHhlgorbGzPLGJ7ZjHbMovYebyEcjdKFk1lMerp1TGAxKhAEqMC6d85iO4Rfuh0kliEtiSJiDZPVVX2Zpex9Wgh2zKL2Z5ZREZBpdZhaS7U18SguBAGdw1lcNdQenSQpCJanyQR0SYVlFbw84FC1hzKZ+2hfPLLbVqH1OadTipXxoWQ3C2M7h38tQ5JtAOSRETboKpwYhsc+B4OfE+2oRNDDt+sdVRuLTbUh9G9OzCmT0cujw1GL30qogVIEhHacdrh4HLY93XNz4qTtXep5gB6lf0bqyKXMjWHUF8To3pHMDqhI8O6h2ExGrQOSXgISSKi9WXvgLTFsOsTqCw4b7FbbQ/ws9K/9eJqJ3xMBob3CGfygCiu7hWB0SCJWrhOkohoHeV5sPMj2PEB5O5u1EMWO1P4s/3WFg6sfQv1NXFt/yhuuDya3p0CtA5HuCFJIqLlOGxw4DtI+wAOLQelaUNwM/Ux/Kby2RYKTpwroVMA1ydFM3lAFCG+Jq3DEW5CkohofllpkPY+7FoCVYUu70ZFR7LtZbKUkOaLTVyUyaBnVO8I5l7VhSu7hmodjmjjJImI5nNgGaz5J2Sub7ZdPsNt/Kd6VLPtTzRNYlQgtw2NY3y/TtJ3AmRkZBAXF8f27dvp37+/1uG0CfKqEJdGccLOT+C1ZFg8rVkTCMBw/Y5m3Z9oml0nSrjvozSGPbuCf688REll680z1hSrVq1i4sSJREZGotPp+Pzzz13az7mPtdvtzJgxg6ioKHbvblxfXnsjSUS4xl4Nm9+ClwfCZ7c3urO8qfqpe9HjbJF9i8bLKa3m79/vZ8gzP/GXz3eTkV+hdUh1VFRUcNlll/Hqq6822z4rKyuZNGkSmzdvZs2aNfTt27fZ9u1JJImIpqkuhdUvwEv94Jv/B0UZLXo4X7WCocaDLXoM0XiVNif/23CUUS/8wp8+2cGxwrYx/cy4ceN48sknmTJlSrPsr7i4mNGjR5OVlcWaNWuIi4trsJzT6eS2224jLi4Ob29vevbsyUsvvVSnzMqVKxk0aBC+vr4EBQWRnJzM0aNHAdixYwcjR47E39+fgIAAkpKS2LJlS+1j16xZw7Bhw/D29iYmJoZ77rmHioq2lcBlKnjROOUnYcO/YfPbYC1p1UOPNaaxyt6rVY8pLsypqHyy9Tifp51g2uUx/P7q7nQMtGgdVrPIyclh+PDh+Pn58csvvxAUFHTesoqiEB0dzSeffEJoaCjr1q3jzjvvpFOnTkybNg2Hw8HkyZO54447+OCDD7DZbGzatKl2jrOZM2cyYMAAXnvtNQwGA2lpaRiNNWvOHD58mLFjx/Lkk0/y9ttvk5eXx913383dd9/NokWLWuOpaBTpWBcXZquoqXmsfxUcVZqEcFgfx6jKpzQ5tmgcs5eem67szF0juhHub9Y0Fp1Ox9KlS5k8ebJLjzWZTHTt2pWtW7fi4+NT5/7GdKzffffd5OTksGTJEgoLCwkNDWXlypUMHz68XtmAgABefvllbr65/hQ/t99+OwaDgddff71225o1axg+fDgVFRVYLG0jaUtzlmiYqsKOD+HlJFj9vGYJBCBOOUqorkyz44uLszoUFq3N4Dd/X8Ez3+1r1YW+mtuECRM4cOBAnQ/vC3n11VdJSkoiPDwcPz8/3njjDTIzMwEICQlh7ty5pKamMnHiRF566SWys7NrH/vHP/6R22+/nZSUFJ555hkOHz5ce9+OHTt455138PPzq72lpqaiKArp6enNe9KXQJKIqO/YZtS3UmDpPCjLvnj5FqZHYaJ5u9ZhiEaosjv5zy+Hufr5lXy4KRNFcb+GjtmzZ/P2229z//3388ILL1yw7Icffsj999/Pbbfdxg8//EBaWhq33HILNtuZWacXLVrE+vXrueqqq/joo4/o0aMHGzZsAOCvf/0rv/76K+PHj+fnn38mISGBpUuXAlBeXs68efNIS0urve3YsYODBw8SHx/fck9AE0mfiDijNAt+/Cvqzo/R0bbe/CMNabzDb7QOQzRSQYWNhz7bxeJNmSyc1IcBnYO1DqlJbr75ZvR6PbfccguKonD//fc3WG7t2rVcddVV3HXXXbXbzq5NnDZgwAAGDBjAggULGDJkCIsXL2bw4MEA9OjRgx49evCHP/yBGTNmsGjRIqZMmcLAgQPZs2cP3bp1a5mTbCZSExE1w3V/eQ715STY+VGbSyAA/ZU9WocgXLDzeAnXvbaO+z/ZQV6ZtcWOU15eXvttHSA9PZ20tLTaZiWABQsWMGfOnEbvc/bs2bz77rs89NBDPPfccw2W6d69O1u2bGHZsmUcOHCAv/zlL2zevLn2/vT0dBYsWMD69es5evQoP/zwAwcPHqR3795UVVVx9913s3LlSo4ePcratWvZvHkzvXv3BuDBBx9k3bp13H333aSlpXHw4EG++OIL7r77bheeoZYjNZH2bvdnqMsfRVdyjLa82kSgWsogr8NscrSdarxoHFWFJVuPs+zXHO4d1Z25V3XBq5mvft+yZQsjR46s/fuPf/wjUFOjeOeddwDIzs6uk1QaY+bMmej1embPno2iKEyfPr3O/fPmzWP79u1Mnz4dnU7HjBkzuOuuu/juu+8A8PHxYd++fbz77rsUFBTQqVMn5s+fz7x583A4HBQUFDBnzhxyc3MJCwvjuuuuY+HChQD069ePX375hYcffphhw4ahqirx8fH1YtCajM5qr0qOo34+H136Sq0jabRFuutYWHW91mGIS9S7UwDP39CPPpGBWocimoE0Z7VHOz5EeXWwWyUQgKt0u7QOQTSDvdmlTH51LS/+eAC7U9E6HHGJpCbSnlQU4Ph8Pl4Hv9M6Epc4MJBkfZ0S1efihYVb6BMZwPM3XCZrmbgxqYm0E86932J/KcltEwiAF06uMcmEjJ7k16xSJr2yhn/9dBCH1ErckiQRT2ctp/qj2zF8NAOjrUjraC7Z1YY0rUMQzczuVHlh+QGm/HsdB3LlolJ3I81ZHkzJWIvj41sxVeZoHUqzKdCFkFT1itZhiBZi9tLz6MQEZl4Zq3UoopGkJuKJHDasX/0J3TvjPSqBAISqhfQzHNM6DNFCrA6Fh5fu5u7F2yirdt+pU9oTSSIeRi3NovrVYZi3vtEmLxpsDuNN27QOQbSwr3dmM+HlNfya1bozRoumkyTiQaoP/oLtX1diKdqndSgtKlm3U+sQRCs4WlDJ1NfW8fEWqXm2ZdIn4iHylz1P0Pq/4dUOVgG0Y6Rf9RtUoe2U46L1TL88hoXX9sFiNGgdijiH1ETcnN1axfH/3EDY+ifaRQIBMGJnrFkuPGxPPtpyjBlvbiC/vOXm3xKukSTixspyMyj451Cic37QOpRWlyJDfdud7ZnFTH51LQdlGHCbIknETeXtXoHy+gg6Vh/SOhRNXM5urUMQGjheVMV1r61j9cE8rUMRp0gScTOqqnLsh1cIWDKNQMX9Lx50VQflJN0NnjV8WTROWbWDWxZtZvHGps3IK1qGJBE34nQ6Ofq/u4ha+whmbBd/gIebaNqqdQhCIw5F5c9Ld/Hk13vccvVETyJJxE1UV1aQ8e8b6HJkMXqdvGkAhsmsvu3eW2vS+e17W7E62segkrZIkogbKDyZzdFXriW+4CetQ2lTeiv7MSFXNbd3P+zJ5bZ3tlBlk0SiBUkibVzmgd3kvH4dPSs3X7xwO2PBSopJls0VsOZQPnPe3ihTpWhAkkgb9uvmVZS9N4sEp3xQns8YrzStQxBtxOaMIma9tZHiSukvbE2SRNogVVXZse5H9F/cRR99utbhtGlXIP0i4owdx0u48Y0N5JXJRYmtRZJIG6OqKmmrv8f729/T20vmDLqYKCWLzvoCrcMQbci+nDKmv7GenJJqrUNpFySJtCGqqrJ1xZf4/3AvPbyytA7HbUyUWX3FOY7kVXDD6+vILqnSOhSP5xZJZOXKleh0OoqLi7UOpcUoisKm5Z8S+vP/o5tXrtbhuJXhBlkyV9R3rLCK2f+3icIK6SNpSZeURJ5++mmuuOIK/P39iYiIYPLkyezfv79J+8jIyECn05GWlla7raysjJEjR5KQkMDx48cvJUS3oCgK65d9SsQvDxLnJdM5NFVfZR+GdjL5pGiaQyfLmbtoE+VWh9aheKxLSiK//PIL8+fPZ8OGDSxfvhy73c6YMWOoqKhweZ95eXmMHDmSiooKVq9eTXR09KWE2OY5nU7WfPsJ/qv+SpwxX+tw3JKPWskIY9O+vIj2Y+fxEm5/dzPVdvmi0RIuKYl8//33zJ07lz59+nDZZZfxzjvvkJmZydatrk1HcezYMYYNG0ZgYCA///wzoaGhDZYrKChgxowZREVF4ePjQ2JiIh988EGdMkuWLCExMRFvb29CQ0NJSUmpTW4rV65k0KBB+Pr6EhQURHJyMkePHq197BdffMHAgQOxWCx07dqVhQsX4nA0/zcZp8PB6q8/RLf67/Qze36NqyWNMW7XOgTRhm04Usjdi7fjcCpah+JxmrVPpKSkZinLkJCQJj92//79JCcnk5CQwLfffoufn995y1ZXV5OUlMQ333zD7t27ufPOO5k9ezabNm0CIDs7mxkzZnDrrbeyd+9eVq5cyXXXXYeqqjgcDiZPnszw4cPZuXMn69ev584770Sn0wGwevVq5syZw7333suePXt4/fXXeeedd3jqqadceEbOz2G3s/LLxVSs/jfDvNvnTLzN6UqZ1VdcxI97c3ng053IOnzNq9lWNlQUhUmTJlFcXMyaNWsa/biMjAzi4uIwmUwkJyezfPlyDIa6q5etXLmSkSNHUlRURFBQUIP7mTBhAr169eL5559n27ZtJCUlkZGRQWxsbJ1yhYWFhIaGsnLlSoYPH15vPykpKYwaNYoFCxbUbnvvvfd44IEHyMpqnhFTiqKw+tuPyf75TaYFbEXvoWuhtyYFHUNsr5KrBGkdimjjbk2O49GJCVqH4TGarSYyf/58du/ezYcffujS4ydNmsTq1av57LPPLlrW6XTyxBNPkJiYSEhICH5+fixbtozMzJqpoS+77DJGjRpFYmIiN9xwA2+++SZFRTXTpoeEhDB37lxSU1OZOHEiL730EtnZ2bX73rFjB48//jh+fn61tzvuuIPs7GwqKytdOrdzbV+znCMr3ue6gB2SQJqJHpWJJmnSEhf39tp0/rfh6MULikZpliRy99138/XXX7NixQqXO8IffvhhHn30UW666SY+/vjjC5Z97rnneOmll3jwwQdZsWIFaWlppKamYrPVDOUzGAwsX76c7777joSEBF5++WV69uxJenrN1d+LFi1i/fr1XHXVVXz00Uf06NGDDRs2AFBeXs7ChQtJS0urve3atYuDBw9isVhcOrez7UvbwLZv3uYGv80yeWAzG6HfqXUIwk0s/PJX1h2WgSzNwetSHqyqKr///e9ZunQpK1euJC4u7pKC+ctf/oJer2fmzJmoqsr06dMbLLd27VquvfZaZs2aBdQ0Dx04cICEhDNVVJ1OR3JyMsnJyTz66KPExsaydOlS/vjHPwIwYMAABgwYwIIFCxgyZAiLFy9m8ODBDBw4kP3799OtW7dLOpeGZB7aw+rP3mKKeR1+OrkIqrldpu4BFNzk8iehIYeictf72/hifjKxob5ah+PWLimJzJ8/n8WLF/PFF1/g7+9PTk7NSnOBgYF4e3sDMGfOHKKionj66acbtc+HH34Yg8HAzJkzURSFGTNm1CvTvXt3lixZwrp16wgODuaFF14gNze3Nols3LiRn376iTFjxhAREcHGjRvJy8ujd+/epKen88YbbzBp0iQiIyPZv38/Bw8eZM6cOQA8+uijTJgwgc6dO3P99dej1+vZsWMHu3fv5sknn3T5ucrLPsbyj95kjPNnwoylLu9HnJ+/Wkay8RBr7T20DkW4geJKO7e9u4Wld12Fv8WodThu65KSyGuvvQbAiBEj6mxftGgRc+fOBSAzMxO9vmnfDB966CH0ej2zZ89GVVUiIyPr3P/II49w5MgRUlNT8fHx4c4772Ty5Mm1o8MCAgJYtWoVL774IqWlpcTGxvKPf/yDcePGkZuby759+3j33XcpKCigU6dOzJ8/n3nz5gGQmprK119/zeOPP86zzz6L0WikV69e3H777S48QzVKiwpY9uGbXF62jFiLzPPUksYat0sSEY126GQ5v/9gO2/ffAV6vU7rcNxSs43OEg2rrqzg6/dexbL/cyb4/6p1OB7vkD6elMontA5DuJnbh8bxyAQZseUKaTxuQQ67nZ+W/pei3T8x1l+uqG4NcUo6wbpyrcMQbuatNel8kXZC6zDckiSRFqIoCmu+X8K+jcuZFroXL2TuntZgQGG8OU3rMIQbenjpbjLyXZ+yqb2SJNJCdm1cyaafv2ZyyCEC1RKtw2lXrtbLrL6i6cqtDn7/wXZsDpkapSkkibSAE+kHWP3NR1zhe4J45KKm1jZQlb4n4ZpdJ0p45rt9WofhViSJNLPy0mJ+Wvo/vCtOMMxLLn7TQpBaTJKXLCssXPP22nR+2itr+jSWJJFm5HQ6+eWrD8g+vJvrgvfgJWtcaOYamdVXXIL7P9khy+s2kiSRZrR9zQ/s2vQLEzvkEKzI9SBaukq3S+sQhBsrqrRzz4fbcSpyBcTFSBJpJscP72Pdss/oE1BOgrJH63Dave7KYZlaRlySTemFvLn6iNZhtHmSRJpBZXkpK758H6WygBQv1xbkEs3LCwfXmKRPSlyafy4/QLoM+70gSSKXSFEU1ny3hGOH9jA+PAdvtXmmixeXbpRBhvqKS2N1KDy4RBayuhBJIpdo37Z17Fj/M306mulml6GlbclAWe1QNINNGYW8J+uPnJckkUtQkHuC1d9+jNFLz3A2ItO3tS3hSj4JBpnKQly6Z7/fz4li6WNriCQRFzmdTlZ/8zGFJ7P5TWgBQU5Z4KYtmmDapnUIwgOUWx08vFRG/DVEkoiL9m9fz4Gdm+kaGUa/qg1ahyPOY6hOOtdF81i5P4/Pth3XOow2R5KIC8pLili//AsMRiND1Q0yuWIb1lM5iDc2rcMQHuKJr/dQUiXLWp/tkhalao9UVWXTiq/JOX6E5FgLUZUyjrwtM2NjtGk3X9oGah1KsytZ/zGVB9ZjLzyOzsuEOao3wcPnYgyNri1jL8qmaMX/YT2+B9VpxzsuiZDR8zD4BjfuGBs+ofiXd/FPmkRIyp212wt/epOK3T+hM1oIGn4zfn1G1t5XsW8NFbt/IuL6x5rvZNuIoko7L/14kEcnytojp0lNpImOHd7LjvUr6BgRwaDqlVqHIxphtFea1iG0iOpju/EfOJ6Os56nw/QnwOkg9+O/oNhqputQbNWc/PgvoNPRYcbf6DjrOVTFwclPH0dVLz5TrTX7AGVp32MM71Jne+WhjVTs/YWIaU8QPOIWCr9/GWdlzUzVirWC4lX/JWTM75r9fNuK/23I4HCerFlzmiSRJrDbrKz7/jOsVZUkm/fho8gLyR1c7qFDfTtMexy/xBRM4bGYIroSOv4POEvzsOUeAsB6Yg+OkpOEXfMHTOFdMIV3IWz8H7BlH6L66IX7ihRbFflfPU/o2N+jt/jVuc9ecAxLTCLmTt3xTRiOzuSDo6RmwsKiFYvwH3ANXgERLXPSbYDdqfLUN3u1DqPNkCTSBDs3rCR9/056RwXQo1om+HMXnZQcuurztA6jxSnWmiurT3/oq86atnudwVhbRmcwgU6H9fiFr2kqXP4a3vFX4N2lf737TOFx2HIO4awux5pzCNVhxSs4kurjv2LLPYx/0sRmOqO26+d9J1l1wPNfU40hSaSRCk9ms/HnL/HxD+Ryx2b0yBWs7mSC2bOno1FVhaKf3sQclYDpVPOTObIXOqOFopWLUOzVKLZqilb8H6gKzvKi8+6rYs8v2HIOEzz85gbv9+6ahG+fEeS8+wcKvvknYeP/gN5opnDZvwlJnU/Z9m858eY8ct77E7Y8z71I74mv98gEjUgSaRRFUVj3w1KK807SI1RPlF06093Nbzx8qG/hD69hyztK2KQHarcZfAIJn/wQVYc3ceyFGzj24jQUawWmDvGga/jSWEdpHoU/vUnYxPvReZnOe7ygoTOJmvcmkbe9ik+PqyhZ/wmWLv3R6Q2UrP+IjjP/jl+/MRR880Kzn2tbcfBkOe9v9Nwk2VgyOqsRDu3ewt5t6wiP6kz/6uVahyNc0EfZhxcOHB74ki9c/hpVhzfT4aZn8AoIq3Ofd9xAoua9hbOyBJ3egN7ix7FXZuET1LHBfdlyDqFUFpP9zr1nNqoK1mO/UrbtazrfvxSd3lDnMfaCY1TsWUGnuf+ifOdyLNF9MfgE4tNrGAXfvYRirURv9mn2824L/rn8AJMHRBFgMV68sIfyvHdUM7NWVbL+h8/R6aCLpYxOpfLNwx15U80o016W2RK1DqXZqKpK0Y//ofLAejrMeBrjeRID1NRKAKqO7kCpKMGn25UNlrPEXkanW1+ps63g25cwhkYTcOXUeglEVVUKlr1K8NW3ozd5g6qgKqeumzr9sxEjwdxVUaWdt1an88fRPbQORTPSnHURe7atI+voQSKiupBYuU7rcMQlGOPlWYMhCpe/RvmvKwmb+Cf0Jh+c5UU4y4tQ7NbaMuU7l2M9sQ97UTblv64g//Nn8L/i2jrXkuR++GdKt34FgN7sUzuS6/RNZzSjt/jX9rWcrXzHMgzeAbVJyRzVm+qjO7Ge2Efp5i8whnauN7rL0yxak05xZfu9oFVqIhdQVVHOttXLMHv7EUkOHR3HtA5JXIJBHjbUt3z7twDkfrCgzvbQa+7DLzEFAHvhCYpWvYtSVY5XYASBQ6bhf8XkOuXtRTmYq0qbfHxnRREl6z+m46znareZI3sSMGgKJ5csRO8TSNj4PzR5v+6mzOrgjVVHeGBsL61D0YROlYnyz2vrqmUs+/gtouN7MbbiUyIcMiOsO1PRkWx7mSwlROtQhIfxNRlY8+DVBPuefzCCp5LmrPOoLC9j+5of8Pb1J1o5IQnEA+hQmWTyrCYt0TZU2Jz835p0rcPQhCSR89izdQ15WZmEdYymX9VarcMRzWS4XlY7FC3j3fUZlFa3v8kZJYk0oKKshG2rf8DbP5AY5ShhjhytQxLNpJ+6Fz1OrcMQHqis2sG7azO0DqPVSRJpwO5Nq8jPPkZoh0gSK2WtEE/iq1YwzHhQ6zCEh1q0LoNqe/v6kiJJ5BzlJUWkrV2Ob2AwEUoeoU6phXiasUbpFxEto7DCxpc7srQOo1VJEjnH7s2rKMjNIjQikm5WaT/3RFciy5yKlvPuugytQ2hVkkTOUlpUQNraH/ELCsGssxNr3a91SKIFdFEyCdeVaR2G8FC/ZpWyOaNQ6zBajSSRs+zZtpbCk9mEhHci3rrbrZa9fXq1lSveLMf/6VIinitj8oeV7M+v2zb7xlYbI96pIODpUnQLSymubtwlQq9ustHlxTIsT5Zy5VvlbDpRd79/XFZNyLOlxPyzjPd31h2d8smvdiZ+UHlpJ9fM9ChMMEuTlmg577Sj2ogkkVOs1VX8umk1Pv6B6PV6ulW716yvvxx1MP8KExtu82X5bB/sCox5r5IK25lEUWlXGdvNiz8PMzd6vx/ttvPHH6p5bLiZbfN8uayDgdT3KjhZUTMf0lf77SzeZeeH2b78PcXC7V9VkV9Zc19JtcrDP1t59RpL855sMxhhSNM6BOHBlu3OIaekWuswWoUkkVPS9+0gP+cYweGd6GDPJEA5/3oLbdH3s3yZ299EnwgDl3U08M61FjJLVLZmn6k13DfYzENDzQyONlxgT3W9sMHKHQON3DLAREK4gf9MsOBj1PH29poax958hRFdDFweaWBGopEAs470oprE9cDyan53uZHOgW3vZdZf2aN1CMKDORSV9za0j8la2967WwOqqrJn61p0Oj1Gk4nuHtChXnJqDr4Q74bXjWgMm1Nla5ZCStczU6zpdTpSunqx/nhNcrqsg4EtWU6KqlS2Zjmpsqt0C9GzJtPBthwn91zZNqeBCFRLudLrsNZhCA/2waZMrA7PH+4rSQTIPZ7B0QO/EhTeEW+lnGibe3+4KKrKfd9XkxxjoG9E42sd58qvVHGq0MG3biLq4Ksjp7ymySq1mxez+hm54s1y5n5RxbuTvfE1we++qeY/4715bYudnq+Uk/x2Bb+ebFtvqHGmbVqHIDxYQYWNZb/mah1Gi5MkAhzYuZmqijJ8/QOJr96JHvde/2D+N9XsPunkw+u9W+V4fx1h4dA9/uz6nR9Teht5erWNlDgvjAZ4cpWVNbf4cPsAI3M+r2qVeBrrKhnqK1rY59s9f869dp9EKsvL2Lt1Df6BIehR6WZ17w+Wu7+t4uuDDlbc7Et0wKX9e8N8dBh0kFtRdxRXboVKR7+G970v38l7u+w8cbWZlRkOfhNrINxXz7Q+RrZlK5RZ286k0fFKOoG6tjVyTHiWVQfyKCi3XrygG2v3SeTInu0U5ecQFNaBKPthfJRyrUNyiaqq3P1tFUv3Ofh5jg9xwZf+rzUZdCRF6vnpyJmhzoqq8tMRB0Ma6JxXVZV5X1fzwhgzfiYdTgXspyp1p386204OwYCT8eY0rcMQHsyhqHzl4Vewt+skoigKuzevwuBlwuDlRWc3vrhw/rfVvLfTzuLrvPE31/RZ5JQrVNnPfGrnlCuk5Tg5VFjzib4r10lajpPCqjNlRv23glc2nVml7Y+Dzby5zc67aTb25jn53dfVVNhVbulff03pt7bZCffRMbFnzX3Jnb34Od3BhuMO/rneSkK4niCL6x39LeFqmdVXtLClaZ6dRNr1yoZZ6Qc4kX6AkIhO6FUnkXb3XQ/gtS01Q25HvFu3eWbRtRbm9q8ZIfWfLTYW/nImQfzmncp6ZQ4XKrXXeQBM72skr1Ll0ZVWcspV+nfU8/1MHzqc05yVW67w1Gor627zrd02KMrA/xtiZvziKiJ8dbw7uXX6aJpigPqr1iEID7fjWDHp+RXEhflevLAbatcrG/746btsXvENsT37Emk7woiypVqHJDQwyf4sO50xWochPNg9o7rzx9E9tA6jRbTb5qzykiL279hIQEgYANG2QxpHJLQyXob6ihbmyaO02m0SOXZ4L2VF+QSEhIOqEuXm14YI1w3VudcUN8L9ZBZWsut4idZhtIh2m0Qy9u8CvR6DwUC44wTeqgz1bK96KAfxwbOHYQrt/bTPMy88bJdJpLK8jPR9O/EPCgEgxiYr3bVnRhyMM0ttRLSsn/ed1DqEFtEuk8iJ9P2UFRfgHxQKSH+IgFEyq69oYbtOlHCyzPNm9m2XSeTogV9RFRUvLyPBjlz8lFKtQxIauxwZ6italqrCCg+sjbS7JGKtruLInm34BgYBUgsRNSKUk/QwZGsdhvBwP+2VJOL2sjIOUlyQR0BwzdBe6Q8Rp02Qob6iha09lI/N4d4TvJ6r3SWRY4f24nQ4MJrM+DhLCXIWaB2SaCOG6dx78k3R9lXYnGw44lmfOe0qiTjsdg7u3oKPfwAA4Q7PvQBINF2Csh8T9osXFOIS/HIgT+sQmlW7SiI5mYcpysupbcoKt0sSEWeYsTLaJB3somVtzijUOoRm1a6SSObhvdis1Zi9fQAIc3j27Jqi6UZ7pWkdgvBwe7JKqbQ5Ll7QTbSbJKKqKkf2bMfi4weAl2ojyJmvcVSirbmC3VqHIDycQ1HZnlmsdRjNpt0kkbLiQgrzcvD1DwQgzJ6FnnY7gbE4jygli856z+r4FG2PJzVptZskkpedSVV5KT5+pzvVpSlLNGySaavWIQgPtyWjSOsQmk27SSL52cdRFAWDV806XNIfIs7nNwaZR0u0rO2ZRTgVz2gJaTdJ5ET6AbyMNav36VSFMIdcnSwa1lfZhwGn1mEID1Zhc7InyzOmW2oXScRaXUXOsSO1/SGBznyMqu0ijxLtlY9ayQjjfq3DEB5uy1HP6BdpF0kkP/sYlXX6Q+T6EHFhqUaZAkW0rL3ZUhNxG/k5x7FbqzGaLQCE26U/RFzYlTLUV7Sw/TllWofQLNpFEsnJPILeYECn0wEQ7PS8mTRF84pRjtFRX6x1GMKDHTxZjqq6f+e6xycRp9PJsSP78PatacrSqQp+Ts9c61g0Hz0qE03btQ5DeLBKm5PMQvdfltvjk0hRXjblxYW1ky76KGUy8kY0ygj9Dq1DEB5unwc0aXl8EsnPPkZ1VXntdCf+Ts+5yEe0rH7qXsCz1n4QbYsn9It4fBIpys8FVYdeX3Oq/ookEdE4/moZyUZZ+VK0HEkibqDoZDZ6L0Pt3/7OYu2CEW5nrFH6RUTL2Zfj/sN8PT6J5OUcx2T2rv1bkohoiiHIaoei5RwrrHL7EVoenUSs1VVUlBZhtpydRKQ5SzRenJJBiK5c6zCEh7I5FfLKrFqHcUk8OomUFRdgrarCdCqJ6FQFX0WG94rGM6AwwSxNWqLlZJVUax3CJfHwJFKIzXomifgqpRhktI1oopF6mdVXtJys4iqtQ7gkHp9EFEXBYKiZ/l2asoQrBqiy7rpoOZJE2rDykrqzZEoSEa4IUotJ8krXOgzhobKKpTmrzSo8mY3By1j7t48iHaTCNdfIUF/RQqQm0kapqkpB7ok6I7NMqntnfKGdq3Qy1Fe0jKwSSSJtkrWqkvLS4tpOdQCj6t5D6YR2uiuH8de5/2R5ou3JkdFZbVNZSSG26qpzaiKSRIRrvHBwjUlGaYnmV1bt0DqES+KxSaSyrASbrRqjyVK7TWoi4lJcbZBZfUXzq7I7cTjd99IDj00iNms1itOJ3nBm3iyTIklEuC5JhvqKFuLOtRGPTSJ2mxWdTle7miFITURcmjA1nz6GE1qHITyQJJE2yG6zwjkTm0mfiLhU403btA5BeKDSarvWIbjMY5OIzVoNZyoh6FWHrGgoLtlQnXSui+ZXbpWaSJtjt1bXqYhILUQ0h17KQbyxaR2G8DDSnNUGWavrXsAj/SGiOZiwMca0W+swhIcpk+astqe6sqJ24kWQkVmi+aR4yRQoonlZHTLEt82prixD73UmiXjhvpletC1XIEN9RfNS3Hh1Q49NIlUVdWsi7vsvEm1NRyWHeEOu1mEID6Io7vsJ5bFJpLqqbhKpM1RLiEs0UYb6imbkxjkEr4sXcT+KomCrrsLgdeZqdVWSiFtzoMOm02PTeWHV6bHpDKf+NmDV6bHX/n3mZtfpsaPHptdhR49dp6tzc3DW7zqwA3adDuep3x06qLRWU1JVhVdgCKrBgFOn4kRl2tqj/PfAc1o/LcINOZxOdDodHcJCarcFDLoV6KJZTJfCI5OIw25DUZzo9ZJEGmLl1Iew3lDzu95Q82GMHrvegO30NnTYdIbaD9raD+ZTvzvg1N+c9WGsO/UBrDt1Pzh1nPW7igNwnPpZ86EMDpTaD+iaMgqKTsWJghMF1aV/n3LqdgksQKAeKK7d5G0zcPm2UsxWGawhLkFRXu2vPlVlGgZyaTwyiZw91clpLZFEFKBaZ2jw23Hdn2e+GdtOfTu263XYzvl2XPMBXP/bsaPO7zU3J2c+iB2nP4jrfAirpz6UlVPbaj6MFVQXWvbUUzf3HUHSnK7dGY7ZelzrMIQH0Z01x5+78cgkcvpT8uxmxiwvE3/okFjv23HNh7Ja+7sT9cyHMgpOHTUfxLUf0ErtB7Oqc6Uhsxm+HQtNJa8vvHghIZpC577d0x6ZRE5PvKieNWyuxGDkR58SDaMSnmDAZuhQLotTiealM7hvEnHfyC+goeYsL9V9q4ui7Zh1MEjrEIQH0vv4aB2CyzyyJoJOh11RKKsoxYoOp+KkzFAF/loHJtxZfL430ZkFWochPJDeP0DrEFzmmUkE2JKVQUZWJlDTqa6YgDhtYxLubfomH3Sq+46iEW2XIcB9v+F6ZBIxGAyExfVADQgiLCgUvV6P6gXL+Vnr0ISb8qs20GevdKiLlqH3lyTS5vj4+BFgtxMe0al2m0E14NTJmiKi6W7YHoTRJlOdiJZhcOMk4pEd6wBGoxFFrTuU1qJaNIpGuDVFZWhahdZRCA+mD3DfPhGPTSJmoxmnUrfW4a16axSNcGejDwbjX1yudRjCQ+lMJvRms9ZhuMxjk4jRaEQ9Z1YzC1ITEU13zRY3nh1PtHnuXAsBD04iAb4B2J111xCR5izRVN3zvImUYb2iBblzfwh4cBIJCgzC6ZDmLHFppm30kak7RYvyCg/XOoRL4rFJxM/Hr95Eg1ITEU3hV22gzz4Z1italjEqSusQLolnJ5FzSBIRTTF9axBedllWWbQsSSJtlK+3L6qq1pmEUZqzRKMpKslpMiJLtDxJIm2Un48fRi8jdseZb5IyOks0Vur+YPxK5doQ0fKMUZFah3BJPDaJ+Pr4YjKasNlttdu8VW90ri2RJ9qZcTKsV7QSk9RE2iY/Hz+MRiP2s9q09ejxV917OJ1oeT1zfeh0XIb1ilZgMODVoYPWUVwSj00ivt6+mLzq1kQAAtVAjSIS7mLaJm8Z1itahbFDB3Re7j2FoccmES8vL/z9/OsnEUWSiDi/wCoveu+XWohoHe7eqQ4enEQAQoNC6yWRANW9pxgQLWv61kC87A6twxDthKlrV61DuGQenUSiOkRhtVnrbJOaiDgfvQJXybBe0YosvXtpHcIl8+gkEh4Sju6c1m1/1V9GaIkGjd0XjE+ZDOsVrcfSS5JImxYeEo7BYKgzQsuAQUZoiQaN3SILlolWpNdj7tlT6ygumUcnkbDgMHwsPlRWV9bZLv0i4lwJOb50PCHzZInWY4qNRe/t/rNoeHQSCQkMwdfXt14SkX4Rca4bNrrvokDCPXlCfwh4eBIxGAxEdYiisqpuEglSg7QJSLRJwZVe9DogtRDRusy9emsdQrPw6CQCENMxpt4IrVAlVKNoRFs0fUsgBocM6xWtS2oibqKhEVq+qi++iq9GEYm2RK/A4B1lWoch2iFLb6mJuIWGRmgBhCvuvZqYaB7X7AnGp7zy4gWFaEbG6Gi8wsK0DqNZeHwSCQsOw8e7/gitCCVCo4hEW5K6VYb1itbnc+UgrUNoNh6fREKDQgkJDKG0vLTOdqmJiMQsXzpkSYe6aH2+gySJuA29Xk9CfALlFXWnswhQA2S53Hbu+k0yrFdow+fKK7UOodl4fBIB6BLdpd5SuSC1kfYstMJIj4MyW69ofcbYzhg7dtQ6jGbTLpJIdMdofLx9qKisOy9ShFP6Rdqr6VsCMDikP0S0Pk9qyoJ2kkQiIyIJCQqhpLykznapibRPeidcuaP04gWFaAE+gzynKQvaSRLx8vKiZ1xPysrrXg8QpAZhVI0aRSW0MunXYLwrqrQOQ7RTnjQyC9pJEgHoGtMVRVHq9Ivo0NHJ2UnDqIQWRm+Vq9OFNkxxcRgjPKsZvd0kkZhOMVjMFqqq634DjVaiNYpIaKH/cT/Cc4q0DkO0U34jRmgdQrNrN0kkqkMUQQFB9a4XiXRGolfbzdPQ7k3dbNI6BNGO+Y8erXUIza7dfHqaTWa6x3anpKxu57oRIx0VzxluJ84vrNxINxnWKzRiCA/De0B/rcNodu0miQD0iOuBw+mod71ItFOatNqDGzcHYnDKsF6hDf9Ro9DpPG9pbi+tA2hNPeJ6EOAbQEl5CUH+QbXbo5xR6FQdqk49/4PbsIr9FeR/m0/V0SocxQ46/74zAUlnVm90VjvJ/SSX0m2lOMudmMJNhKaEEnJ1yHn3WbiykOJ1xVQfrwbAu4s3Ha7vgE9Xn9oy+d/lk/dtHgDh14QTNu7MhHKVhyvJ+m8W8Y/GozNo/8bxcsKgnSUXLyhEC/FP8bymLGhnNZHIiEhio2IpKKrbpGHBQpjivjNqKlYFS2cLkbMjG7w/54McyneVE31nNN3/1p3QMaFkvZdF6fbzXytRsa+CwCsDiXswjvhH4jGGGMl4LgN7Uc1syNXHqsldmkvM72KI+V0MuZ/lUn2sJuGoTpWsd7OIvDmyTSQQgEm7grFUyrBeoQ19YCC+Hja097R2lUR0Oh0DEgZQVV3lUU1a/v386TC1Q53ax9kqD1USlByEX28/TOEmQkaEYImxUHXk/B+qMb+NIXRUKN6x3pgjzUTdGgUqlO+pmYPMmm3FEm3BL8EPvwQ/LDEWrNk1i3/lf5ePb0/fOrUWraVss1+8kBAtxH/EcHRGz7wmrV0lEahp0vLz8aO8su6EjDFKjEYRtTyfbj6UpZVhL7Kjqirle8ux5drw6+vX6H0oVgXVqWLwNQBgjjZjy7VhK7Bhy7dhzbFijjZjPWmlaHUREde1nbHwA4/5EZZbrHUYoh3zS0nROoQW0676RAA6d+pMVIcoTpw8gb+vf+12X9WXYCWYIr3nXUPQaVYnst7JYv8f9oOhpkYWeUskvj0bv7pj7ie5eAV54ZdQk3gskRY6TO1AxnMZAHS8viOWSAvpf0+n47SOlO8u5+TnJ9EZdHSa2alJx2puUzfJsF6hHb2vL37DhmkdRotpd0nEYDAwsM9ADmQcqHdfF0cXikyel0QKfyyk8nAlne/tjCnMRMX+CrL/l40xyIhfn4vXRvK+zqNkYwlxD8WhN52pvIZcHVKnc75oTRF6ix6fbj4ceOgA8Y/FYy+yc+y1Y/R4rgd6Y+tXfDuUmog/lN/qxxXitIBrxqG3eO6yE+2uOQugZ1xPLCYLlVV1VzuMc8Z53IWHik0hd0kunW7sRMCAACwxFkJTQgkcFEj+dxf/cM3/Lp+8b/Locn8XLDHnfyM4yhyc/OIkkbMiqTxSibmjGXNHM369/VCdKrYcW3OeVqPduDkAvaJocmwhAIKuv17rEFqUZ31iNlJcdBwdwjtQUFx3lJYZMzFOz+obUZ0qqlOt/5/WU29wwbnyvs3j5Jcn6fL/uuAd533BstmLswkbE4YxxAhKzXHrxKC0/vBpo0NH0u7iVj+uEKeZu3fD+7LLtA6jRbXLJGI0GklKSKKsoqzefd2c3TSI6NI4q51UHa2i6mjNaCtbvo2qo1XYCmwYvA349PQh56Ocmg71PBtFq4soXltcZzTX8TeOk/NJTu3fed/kcfKzk0TdGoUxzIi92I692I6zuv7FeuW7azrqQ0bVNG15x3ljzbZStrOMwpWF6PQ6zJ1afxXBa3cFY6msbvXjCnFa4NSpWofQ4tpdn8hpCd0T+OaXb6isqsTH+8xQ1AglAn/FnzJ9/QTTVlWlV5HxbEbt3zkf1CSDoOQgou+IrrmOY0kux18/jrPCiTHUSIepHQgZeaY/w1Zgg7Mu6Sj8uRDVoXLs1WN1jhV+bTgdpnSo/VuxKWS9l0XM72LQ6Wt2YAwx0mlWJ068dQKdUUf07dF1+lJaS8o2bZrQhADQGY0EXnut1mG0OJ16sTYND+VwOHj69ac5mnWUrjFd69y312svacY0bQITzWJQpj/3v+95gySE+/AfO5boF/+pdRgtrl02Z0HNQlVXDbyKquoqlHM6Xrs6unpcB3t7M2Vju61kizbC0zvUT2vXn5T9e/cnNCiU/KK6o5TMmN36Cvb2rlOJibgjMluv0I5XZCd8rxqidRitol0nkdCgUJL6JtWbSwsg3hmvQUSiOdy42V+G9QpNhdx0Ezp9+/h4bR9neQGX970co5ex3jUjHZQO+Cv+53mUaKtMDh0Dd8tsvUI7en9/gm68UeswWk27TyI943rSJboLufm5dbbr0NHL0UujqISrpuwMxlwlw3qFdoKnT8Pg1/h56dxdu08ipzvYK6sr63Wwxznj8FHazky04uKu3mrVOgTRjumMRoLnzNE6jFbV7pMIQP9e/QkJDKl3BbsBg9RG3MiQDH+C86UpS2gnYNJEjBFtZwbr1iBJBAgLCWNgn4HkFebVuy/eGY9Zbf2rrUXTXbtJhvUKDel0hN52m9ZRtDpJIqcM6T8Ei9lCaXnd1f688JLaiBuILjbTJV2G9Qrt+F19NeauXS9e0MNIEjmlZ9eeXNbzMrJys+rd193RHZMqa1K0ZdM3+8mwXqGp0NvbXy0EJInU0ul0jBw8Ei8vL8or6q56aMRID0cPjSITF2O26xggs/UKDflccQU+AwZoHYYmJImcJaFbAn269+F4zvF69/V09MRLlTb3tmhqWgimahmVJbQT/oc/aB2CZiSJnEWv13P14KsxGAz1Lj40YaK7o7tGkYkLGbG9SusQRDvmN3w4PgPbZy0E2vFU8OeT2CORXl17sffIXnp0qduE1dvRm0Neh7Dr7BpFJ86VfCSAoIJCrcNocR8WFfFhcTEnHDWvvW4mE78LDeM3py5q+7i4mG9KS9hjtVKhKGzo1p0Ag+GC+3wlP49/F9QdjBBnMvFN3JnO4WdP5rK0pAQfvZ4/hIczMSCw9r7vy0r5sqSEf0d71kJuTaLTEf6H+7SOQlOSRM7h5eXF1UOuZu+hvVRVV+FtObOinxkzfR192W7crmGE4mzXbr7wB6Wn6GD04g/h4cSaagZ4fF5Swt0njvNplzi6m81UKwpDff0Y6uvHP/PrD1U/n24mE/8X07n277M/EFaUl/F1aSlvxcRw1GbnkZxshvr4EuzlRZnTyUt5eXUe2x4FjB+PpVf7Hr0pzVkN6N+rP927dOdE7ol69/Vw9JA5tdqImCILndMvvk68Jxjp589wPz+6mEx0MZm4LzwcH72enVU1TXlzQkK4IzSUy7wtTdqvQacj3Mur9hbsdSaNHLHaGOTjQ1+LN+MDAvDT6zlur6kJPZ+Xx41BwUQajc13km5GZzIR0c5rISBJpEFGo5FRV43C4XBgtdXtsNWjZ4C9/bZ/tiU3bvJF3w7XVHOqKt+WllKlqlzm7X3xB1xAps3G8EOHGHPkMH/KyiLLfqaptqfFzO7qakqcTn6trqZaVelsMrG1spK91mpmBQdf6qm4teBZszBGRWkdhuakOes8BiQMoFtsN9KPp9O9S90O9Sglio7OjuQYcs7zaNHSvO16+v/avlYuPGCtZsbRo9hUFR+9nn9FRtHN7PpsCv0s3jzVqRNxRhN5Tgf/zi9gduZRvoyLw1dvYKivHxMDqph2NAOLTs/THTvhrdfzeG4uf+vUiQ+Li3m/qIhgg4G/duxI90uIxd3oAwMJ++08rcNoE6Qmch5mk5lrRlwDUO+6EYCB9oHoVF297aJ1TN0ejNHavtZQ72Iy81mXOD6M7cL0oCD+nJPNIavrQ5t/4+fHWP8AelosDPX14z/R0ZQpCt+XltWWuTssnGVd4/kiLo4Uf3/eLChgiK8PXsB/CvJ5r3NnpgYFsiC7/kW6niz897/HEBCgdRhtgiSRCxiYMJCkvklkZmVy7lL0gWog3ZzdNIpMDG+Hw3pNOh2xJhN9LBb+GB5BT7OZ/xU1X20swGCgi8nEUXvDyfmI1cpXpSX8PiycTVWVXO7jQ4iXF2P9A06NCnM2WyxtmaVvH4JvmqF1GG2GJJEL0Ov1XDP8GgL8AuotoQuQaE+U6VA0MPxQAIGFpRcv6OFUwK4231QvFYpCps1GuFf9Vm5VVflrbg4PRkTgq9ejqOA49cXq9E9ne+ie0uvpuHBhu1m1sDHkmbiIrjFdGT5oODn5OTiddb9pmTGTaE/UKLL2a+Lm9veyfSHvJFsqKzlht3HAWs0LeSfZVFnJhFPXbeQ5HOytribTVtMxfsBqZW91NcVnvWZvOZbJ+2fVXP5+8iSbT+1ze1Ul95w4jkGnY7x//WaaJSUlhBi8GOlXMzJxgLc3Gysr2VFVxbtFhcSbTBe9LsUTBM+ahXefPlqH0aZIx3ojpCSnsGX3Fk7knqBzZN1x8d2c3TisHKZYX6xNcO1MlwJvYo62v9l6C51OHsrOIs/pxF+vp4fZzJvRMVzl6wvAR8VFdS4cnHMsE4CnOnZkSmAQAMdsNoqcjtoyuQ4792dlUaw4CTEYGOjtzQedYwk5pyaS73DwekE+i2Nja7f18/ZmbnAIvz1+jFAvL/7WsVNLnXqboQ8PJ+Lee7QOo83Rqec29osG/bT+JxYtWUR8bDxmU91RKIW6Qn4w/4Cqk6eypT34XShJabkXLyhEM4t6+V8EjB6tdRhtTvtrF3BR8sBkesf3JjMrs959IWqIrDnSCnysevrtaV/DekXb4DP8N5JAzkOSSCNZzBauGXENOp2u3sJVAImORAIUGfLXkq5PC8Zoa1/DekUbYLEQ+dhjWkfRZkkSaYLLel3G5YmXcyz7WL0hvwYMXGm/Uq4daUG/2V558UJCNLMO99+PMTJS6zDaLEkiTaDX65mcMpmIkIgG1xwJU8KkWauFXH0giICisosXFKIZWa66ipBZM7UOo02TJNJEkRGRTBw1kYrKinprjkBNs1aQEtT6gXm48Vu0jkC0N2pAADHP/V3rMNq8NplEVq5ciU6no7i4WOtQGjQsaRgD+wwk43hGg81ag22D0att8ql1S/H53kRntr9hvUJb0X9/Fq/QUK3DaPOa9En32muv0a9fPwICAggICGDIkCF89913TTpgRkYGOp2OtLS02m1lZWWMHDmShIQEjh+v30zU1hiNRqamTiU0OJSs3PpzBgWrwSQ65CLE5jJ9kw86GYkuWpH52kkEjBihdRhuoUlJJDo6mmeeeYatW7eyZcsWrr76aq699lp+/fVXlwPIy8tj5MiRVFRUsHr1aqKjo13eV2uK6RTDhJETKC0vbbBZq7ejNx2cHTSIzLP4VRvos9fzVy4UbYfSqRNdHn9c6zDcRpOSyMSJE7nmmmvo3r07PXr04KmnnsLPz48NGza4dPBjx44xbNgwAgMD+fnnnwk9T9WxoKCAGTNmEBUVhY+PD4mJiXzwwQd1yixZsoTExES8vb0JDQ0lJSWFiooKoKZ5bNCgQfj6+hIUFERycjJHjx6tfewXX3zBwIEDsVgsdO3alYULF+JwOLiYEYNGcEW/K0g/no6i1J3DSIeOZFsyPopPU58WcZYbtgdhtMlyxKJ1KAYDca++gr4dTWt/qVxuuHc6nXz44YdUVFQwZMiQJj9+//79JCcnk5CQwLfffovfqbWiG1JdXU1SUhLffPMNu3fv5s4772T27Nls2rQJgOzsbGbMmMGtt97K3r17WblyJddddx2qquJwOJg8eTLDhw9n586drF+/njvvvBOdrmYo7urVq5kzZw733nsve/bs4fXXX+edd97hqaeeuug5GI1Gbhh7Ax3DO5KZXf8iRDNmhtqGSv+IqxSVoWkVWkch2pGgu+/GJyFB6zDcSpOnPdm1axdDhgyhuroaPz8/Fi9ezDXXXNPox2dkZBAXF4fJZCI5OZnly5djOGfitpUrVzJy5EiKiooICgpqcD8TJkygV69ePP/882zbto2kpCQyMjKIPWt+H4DCwkJCQ0NZuXIlw4cPr7eflJQURo0axYIFC2q3vffeezzwwANkZTVujYQ1W9bw1idv0TG8IwF+9S84PGw4zCbTpkbtS5wxen8Qd3zWPpa/FW3AsKH0fvNNraNwO03+ityzZ0/S0tLYuHEjv/vd77j55pvZs2dPkw88adIkVq9ezWeffXbRsk6nkyeeeILExERCQkLw8/Nj2bJlZGbWfPu/7LLLGDVqFImJidxwww28+eabFJ2arTQkJIS5c+eSmprKxIkTeemll8jOzq7d944dO3j88cfx8/Orvd1xxx1kZ2dTWdm4i9uuGngVQ5OGkpmVid1ev+kl3hlPV0fXRu1LnHHNFulMF63DFhlJj5df1joMt9TkJGIymejWrRtJSUk8/fTTXHbZZbz00ktNPvDDDz/Mo48+yk033cTHH398wbLPPfccL730Eg8++CArVqwgLS2N1NRUbKemwDAYDCxfvpzvvvuOhIQEXn75ZXr27El6ejoAixYtYv369Vx11VV89NFH9OjRo7Yfp7y8nIULF5KWllZ727VrFwcPHsRisTTqXPR6PTeMu4He8b05lHmo3rBfgMvtlxOihDTlKWrXuud5EynDekUrsFksxP/fWxga+X4XdV1yY72iKFhdXKLzL3/5C3/961+ZOXMmH3300XnLrV27lmuvvZZZs2Zx2WWX0bVrVw4cOFCnjE6nIzk5mYULF7J9+3ZMJhNLly6tvX/AgAEsWLCAdevW0bdvXxYvXgzAwIED2b9/P926dat30zdh4ZlA/0BmXTuLsKAwjmYdrXe/AQNDbUNlEatGmrbRB5lARrQ0Racj6InH8YuL0zoUt9Wk9UQWLFjAuHHj6Ny5M2VlZSxevJiVK1eybNmy2jJz5swhKiqKp59+ulH7fPjhhzEYDMycORNFUZgxo/6yk927d2fJkiWsW7eO4OBgXnjhBXJzc0k41QG2ceNGfvrpJ8aMGUNERAQbN24kLy+P3r17k56ezhtvvMGkSZOIjIxk//79HDx4kDlz5gDw6KOPMmHCBDp37sz111+PXq9nx44d7N69myeffLIpTw9x0XFMu2Yab378JgVFBYQG1x1t5qv6cpXtKn4x/SLTxl9AQJWBPvtkWK9oeY6bZhA7caLWYbi1JiWRkydPMmfOHLKzswkMDKRfv34sW7aM0WdNkZyZmdmkb/AADz30EHq9ntmzZ6OqKpHnTHb2yCOPcOTIEVJTU/Hx8eHOO+9k8uTJlJSUABAQEMCqVat48cUXKS0tJTY2ln/84x+MGzeO3Nxc9u3bx7vvvktBQQGdOnVi/vz5zJs3D4DU1FS+/vprHn/8cZ599lmMRiO9evXi9ttvb9I5nDa4/2CO5xzn8x8/x8fbB2+Ld537Oymd6Ofoxw7jDpf23x5M2xaEl13WDBEtqzwpicsfeUTrMNyeLErVAqw2K69/+Dobd2ykV9de9UafAWw1buWA14EGHt3OKSpvv2bBr1SG9oqWU96pE/2++hLzBS4tEI0jFzC0ALPJzE0TbiIuOo5DRxvuaB9oH0hnR+cGHt2+pe4PlgQiWlRFYCDdFr0tCaSZSBJpIWEhYcycNBM/Hz+yTta/3kSHjsH2wTI1yjnGybBe0YIqvb2JePlfBHfponUoHkOSSAvqHd+b61Kvo6KygqKS+su6GjAwzDZMhv6e0jPXh07HZVivaBnVRiPGvzxC50GDtA7Fo0gSaWEjrxzJ2GFjyT6Z3eCyukaMDLcOx0+RqvW0Td4yrFe0CJteT/mdd5A4ZYrWoXgcSSItTK/XMzV1KiOHjCQzK7PBGX8tWBhpG4lFbb8XOwVWedF7n9RCRPNz6nTkTr2OwfPm1c6ZJ5qPJJFWYDQauWnCTQwZMITDxw5jtdW/ONNP9WOEdQRG1ahBhNqbvjUQr0bMnCxEUyjA8dQx/GbBAowmudC3JUgSaSXeFm9unnIzAxIGcDDjYINTzQerwfzG9hu81CZdvuP29ApclVaudRjCwyjA0aFDGbpwIRYfWZKhpUgSaUUBfgHcet2t9OraiwPpB3A6nfXKRCgRjLSObFc1krH7gvEpk2G9ovkowOGrhpD8zNP4BQZqHY5HkyTSysJCwrj1+lvpHNmZgxkHG7yGJEwN42rr1ZjV9rEwztgt9ZOpEK5y6nTsvfJKhjz5JIFhYVqH4/EkiWggumM0t15/K+Eh4RzOPNxgIglRQxhlHYW36t3AHjxHn2xfOp6QebJE83DqdOy64nKGPPYo4edMnyRahiQRjXSL7cbc6+bi6+3LkWNHGkwkgWogo6yjPHqJ3es3tY/almh5Dr2ebQMHMHjBAqK6yvo9rUWSiIYSeyZy2w234e/jf97pUfxVf1JsKR55HUlwpRe9DkgtRFw6u17P1ssvJ3nBAuJ699Y6nHZFkojG+vfuzx3T7yAkMIQD6QdQFKVeGV/VlxRrCgFK/aV33dn0LYEYZFivuEQ2g4Ftg69k+IKHiO/bV+tw2h1JIm1An+59uHP6nXQI7cCBjIYTiTfepFhTPGaKFL0Cg3eUaR2GcHNlZjNbfjOMqx96SGogGpEk0kb07NqTeTPmERURxf70/Q0O/zVjZpR1lEfM/nvNnmB8yhu3hr0QDcnz8yPt6pGMvf9+OvfooXU47ZYkkTYkvnM8v73pt8RGxrL/yH4czvpNPV54kWxPJtGeCG484e3YLdKMJVyXERLM3pRRTLz3XqLi47UOp12TJNLGxEbG8rubfke32G7sP7Ifu8PeYLm+jr4MtQ3FoNZf8KqtS8zyJSK7/qzGQjTGrk4dyUxJYfL8+XSSKd01J0mkDYrqEMVvZ/y29sr2amt1g+VilBhSrCluNwRYhvUKVyh6PWtjY6kcPZqpv/sdHWJitA5JIMvjtmkFRQX89/P/snnXZmI6xRDo3/D0DVVUsdq8mgJ9258FN7TCyCv/tmFwyFXqovGsZjOrYjsTmZrK2FmzZCqTNkSSSBtXWVXJku+X8NP6nwj0D6RjeMcGyzlxssm4iQyvjNYNsInm/xLG8HU5Woch3Eh+cDDrusQyYOJERkydisksNdm2RJKIG3A6nfyw5gc+//FznE4ncTFx510XYZ9hHzuMO1B09YcJa03vhEWvGvGuqNI6FOEGVJ2OfdHR7O8Sy4ipU7lyzBj0emmBb2skibiRLbu3sPirxeQV5NG9S3e8vBqeMr5IV8Q60zpK9fVXUtTS5J3B3PRNntZhCDdgs1hYF9uZqrg4xs6cScIVV2gdkjgPSSJuJv14Ou8ufZcD6QeI7xyPt6XhCRodONhu3M4hr0OtHOH5vbrIn/AcGZUlLqw4PJyfO3YgtGdPxt98MzHdu2sdkrgASSJuqKC4gPe/fJ+NOzYS1SGKoICg85Y9rj/ORtNGbDpb6wXYgP7H/fjz/4o1jUG0bapOx+GuXdkSGEDvQYMYc9NNhEREaB2WuAhJIm6q2lpd2+FuMproHNn5vP0kVVSx3rSeXENuK0d5xhNLQ+i576RmxxdtW7WvL5u6dKEgJJgh48aRPH68dKC7CUkibkxRFNZvX89nP3xGTn4O8Z3jsZgtDZZVUdnntY+dXjtbvdM9vMzEv16zYmhgKhchsrp2ZY2/H6FdujB6+nR6DBhw3i9Eou2RJOIBTuSe4MNvPmT7r9sJDQklIiTivG/CQl0hG00bKdYXt1p8v18RxrANMqxX1GX19WVnQm8OOZ30vuIKUm+6iZAOHbQOSzSRJBEPYbVZ+X7V93y36juqrdV0jel63tFbCgoHDQfZadyJQ9eyc1h5OeHtV4xYKmVYr6ih6nTk9OjOxuBgVKNRmq/cnCQRD/PrwV/5+NuPOXj04AWvcgeopJLtxu1kemW2WDzXpQVz43cyrFfUqAwMZM9l/ThQVkbH2FhSpk2T5is3J0nEAxWXFfPZss9YtXkVZpP5gp3uANn6bLYYt1CuL2/2WP79th9hucXNvl/hXpxGI8f79mG7jw92h4N+Q4cycsoUAsPCtA5NXCJJIh5KURTWblvL0h+WkpufS0xkDAF+518Z0YmTPV572OO1p9k63gce8+Oh94qbZV/CPak6HXnx8ezvFs+x3FwioqMZMWUKfQYPlqvPPYQkEQ+XdTKLL3/6kk07NoEOYqNiMXoZz1u+TFfGFuMWcgyX3hH+1KchdD8gw3rbq9IOEaQPGMCh0lJUVSXxqqsYPnkyweHhWocmmpEkkXZAURS27dnGlz99yaGjhwgPCSci9PwjuACy9FnsMu6iUF/o0jE7lJp46bVq9A0s9Ss8W7WfL5kDB5Lh709+VhaRcXEMnzyZXpdfLrUPDyRJpB0pqyjjx3U/8uPaHykpKyE2OhZfb98LPuaY/hi7jLso0Zc06Vj3/hRG8iYZ1tueOIxGsvv2Ib1LF7KPH8fs40P/YcMYOn48/sHBWod3UStXrmTkyJEUFRURFBSkdThuQ74WtCP+vv5MGT2F+2+/n8sTL+d49nEyjmc0uJ77aTFKDOOs4xhiG4Kf4teo4xgdOpJ2FzdT1KKtc5hMHL+sH1smTWSTjw85WVn0GDCAmX/8I2NnzmzWBPLMM8+g0+m47777mvS4jIwMdDodaWlptdvKysoYOXIkCQkJHD9+vNlibG8avpBAeLS46DjunnU3G3ds5KsVX7H38F46hHUgLDiswSYuHTq6OLvQ2dmZdEM6u712U6mvPO/+r90VjKVS+kI8nd1sJqd3b7J79OBkQT6l6elEx8dz1TXXkHDFFRjOc52SqzZv3szrr79Ov379LnlfeXl5jBs3Dr1ez+rVqwkNDeXQobYzWak7kZpIO+Xl5UVyUjIP3vkgk66ehM1uY8/BPRQUF3C+Fk49euKd8UywTiDJloS32vAMwilbtZ3sUbQsu9lM5oABpF03hX3RURw+dBCD0UjqzJnMefBBEocMafYEUl5ezsyZM3nzzTcJvsSazbFjxxg2bBiBgYH8/PPPhIaGNliuoKCAGTNmEBUVhY+PD4mJiXzwwQd1yixZsoTExES8vb0JDQ0lJSWFiooKoKZ5bNCgQfj6+hIUFERycjJHjx6tfewXX3zBwIEDsVgsdO3alYULF+JwtOzFvy1BaiLtXHBAMDdOuJGhlw/l5/U/sz5tPTknc4jsEElQQFCDNRMDBno4exDvjOeo4Si7nbuo8K6pmQw6GkBInmud8aJts3l7k53Qm5M9elBWVcXJgwcx+/gwaPRohowbR2jHhlfdbA7z589n/PjxpKSk8OSTT7q8n/379/OnP/2Jyy+/nA8++ADzBa6Sr66uJikpiQcffJCAgAC++eYbZs+eTXx8PIMGDSI7O5sZM2bw97//nSlTplBWVsbq1atRVRWHw8HkyZO54447+OCDD7DZbGzatKn2/bR69WrmzJnDv/71L4YNG8bhw4e58847AXjsscdcPj8tSMe6qCP9eDo/rfuJzbs2U1FVQVSHqAte9Q6w+avvwN+Kc2Qwd35dTfxBacryJKUdIsjt2ZOizp0pKysj78QJTBYLPfr3Z1BKCp179mzRK84//PBDnnrqKTZv3ozFYmHEiBH079+fF198sdH7yMjIIC4uDpPJRHJyMsuXL8dgMNQp05iO9QkTJtCrVy+ef/55tm3bRlJSEhkZGcTGxtYpV1hYSGhoKCtXrmT48OH19pOSksKoUaNYsGBB7bb33nuPBx54gKysrEafV1sgNRFRR1x0HLfdcBvDrxzO8rXL2fbrNrJys4juFI2/r3+98kV5eTjyS+gf0Z/4gl6U9Skl22s/4YeP4GWTZi135fTyIr9rHLk9e1IZFERFSQkn9+7F4uND4pAhXD5qFLEtnDygpunp3nvvZfny5VgsDc9Q3RSTJk3i888/57PPPuOGG264YFmn08nf/vY3Pv74Y06cOIHNZsNqteLj4wPAZZddxqhRo0hMTCQ1NZUxY8Zw/fXXExwcTEhICHPnziU1NZXRo0eTkpLCtGnT6NSpEwA7duxg7dq1PPXUU3WOV11dTWVlZe0x3IHURMR5qarKviP7WL52OWl703A4HHSK6ESAX0Dth8eOFb/A0QJGXzOpzoSPeoeD0CPpdDhwAN9Cad5yF1UBAeT27EF+fDwOo5Hy4mLys7Iw+/rSa+BALh85kpgePVptrqvPP/+cKVOm1Kk1OJ1OdDoder0eq9Var0bRkNM1ke3bt/PVV1/x+OOP8/777zNt2rTaMufWRJ555hmef/55XnzxRRITE/H19eW+++7Dy8uLzz//HKh5j6xbt44ffviBpUuXkpOTw8aNG4mLiwNg+/btfP/993z11Vfs2rWL5cuXM3jwYLy9vVm4cCHXXXddvVi7du3qVtfTSE1EnJdOp6N3fG96xvVk98HdrNy4kt0HdnM85zgRoRH4WXyoPJZLt+i4ejMGK15e5PXoTl6P7ngXFxN6JJ2w9HTMpzodRdvhMBop7NyZgq5xlHbsiKKqlOTnU3TyJN5+fvT/zW9IGjmSmO7dW32ixFGjRrFr164622655RZ69erFgw8+2KgEcq6//OUv6PV6Zs6ciaqqTJ8+vcFya9eu5dprr2XWrFlAzUW7Bw4cICEhobaMTqcjOTmZ5ORkHn30UWJjY1m6dCl//OMfARgwYAADBgxgwYIFDBkyhMWLFzN48GAGDhzI/v376datW5Pjb2skiYiL0uv19OvZj8QeiRzOPMz67evZtHMTuzZtxMumEBd/4TWwq4KCOD5wAMcH9Mf/5EnCjhwh5GimNHdpyGkwUBwdTUFcF4qjolANBmzV1RQcPUpleTmBoaFcmZrKZcnJRMXHazbLrr+/P3379q2zzdfXl9DQ0Drb58yZQ1RUFE8//XSj9vvwww9jMBiYOXMmiqIwY8aMemW6d+/OkiVLWLduHcHBwbzwwgvk5ubWJpGNGzfy008/MWbMGCIiIti4cSN5eXn07t2b9PR03njjDSZNmkRkZCT79+/n4MGDzJkzB4BHH32UCRMm0LlzZ66//nr0ej07duxg9+7dlzRwQAuSRESj6XQ6usV2o1tsN8YMHcPyZV9xcOU6CrKyKc49SVinTvj41+83OWsHlHXoQFmHDmQMGkTQiROEHUkn8MQJWfWwFSg6HSWRkRTEdaEoJgbFaERVVcqLiynIzUWn09Ghc2dGTp1Kr4EDCXKjOa4yMzOb3AT00EMPodfrmT17NqqqEhkZWef+Rx55hCNHjpCamoqPjw933nknkydPpqSkZvaGgIAAVq1axYsvvkhpaSmxsbH84x//YNy4ceTm5rJv3z7effddCgoK6NSpE/Pnz2fevHkApKam8vXXX/P444/z7LPPYjQa6dWrF7fffnvzPCGtSPpExCWprqzkYFoaO9au5ej+/VgrK/EPDiYoPByjydSofegcDgJzcgg6cYLAEyewlEuTV3Oxm0yUdupEcVQkxdExOCw1Q1oddjtFeXmUFRbiExBAfN++JA4ZQte+fWVxKNEkkkREs1AUheOHDrF/+3b2bdlCQW4uqCqBoaEEhIY2qe3au7iYwBMnCDpxAv+TeTKJYxOoOh0VoaEUR0ZSEhVJeWgonPqG7nQ6KS0ooLigAJ1OR3B4OIlDhpBwxRV06HzhNWeEOB9JIqLZVVdWcnTfPg5s386BHTsoLSjAYDQSFB6Of1DDFzCej8FmIyA7h4DcXPzy8vApKpKkco5qf3/KIiJqEkdkJ5xn1SQURaGsqIji/HwUp5OAkBC69+tHt8suI653b7z9GjcfmhDnI0lEtKiyoiKO/PorezZvJvPAAcpLSjBbLPgHB+MfFIS+iaNrdA4HfgUF+OXl4ZeXh39ePsbq6haKvu1xmEyUh4XV3irCQnGcc/2EoiiUl5RQnJ+Pw2bDPyiIuIQEeg4YQFxCAn4yQ61oRpJERKtQVZWCnByO7N7NwR07yEpPp/xUB6VfUBABwcGYvRuei+tizGVlp2opxXiXlGApKcFSXo7OzV/aNm9vqgP8qQoKqkka4eFU+/vDOTU5VVWxVlVRVlxc85yqKr4BAUR17UrvK64gLiFBFoISLUaSiGh1qqpSWlDA8cOHyTxwgEM7d1Kcn4/dasXs40NAcDC+AQFNrqWcTed0YiktxbukFO+S08mlFFNlJUartRnP5tI4vQxU+wdQHRBAVWDNz9M35wUGJjidTsqLiykrKsJmtWIymwkMC6Nrnz507tGDqPh4gsPDpZ9DtDhJIkJzNquVnIwMjh06xMGdO8nNzKSyvBxVUTBZLPgGBODr74/RbG6WD0Wd04mxqgpTVRXGqiqMlWf9XlWFwW5H73Sidzhqfp79+zn9MapOh6rXo+j1qAZDnZ+K0YjdbMZhNuOwmLGbLdi9vbH7eGPz9sbu7Y3DbK5XsziXqqrYrVYqysqoLCvDWlWFTq/HLzCQyC5diE9MJKprVzrGxjZ6RJwQzUWSiGhTVFWlKC+PvOPHOXn8OJkHDpB77BgVpaU47HZ0Oh0+/v74BgRg8fFp9inHL0pR0J+6pkUxGGpHPjUnp8NBZXk5lWVlNclUVTEajfgGBBAeGUl09+507NyZqK5dCQgJafbjC9EUkkREm1dVUUHe8ePkZWWRlZFB5v79lBUXU11ZiXqqZmA0m7H4+GDx9sbs49Pmv5GrqorDZqO6qgrrqZvt1ACB04kyIDSU2B49iIiJITwykvDISBlNJdocSSLC7TidTorz8ijOz6f41BxPp5NMVUUF1srKmiV/VRWdwYDRaMRoNuNlNGI0mWp/N3h5tUifgaqqKE4nDrsdu81W89NqxWG3Y6uuRlEUUFW8TCbM3t54+/oS0rEjEdHRBIaGEhweTnhkJIFhDa80KURbIklEeAyn00lZYSHFBQUU5+dTWlBAWXExpQUFlBYVUVlejsNmw37qpjidZ/ojVLXmdupvvV6PzmBAr9OhNxhQVRVVUWoSxKmf6rnXq+h0oKqoqoreYKhJWqcSmMliISAkhOCICEIiIggICSEwNJTAkBD8goNdmkhQiLZAkohoNxx2O5VlZVRVVFBZXk5VeTlVFRU4TtUWnA4HDoejpuZQXY3NZsNeXY3dakV3VlIwGI01NZlTf+sNBvR6PSaLBYuPT+1Ps7c3Pv7+ePv6Yvb2llqF8EiSRIQQQrjMfVY+EUII0eZIEhFCCOEySSJCCCFcJklECCGEyySJCCGEcJkkESGEEC6TJCKEEMJlkkSEEEK4TJKIEEIIl0kSEUII4TJJIkIIIVwmSUQIIYTLJIkIIYRwmSQRIYQQLpMkIoQQwmWSRIQQQrhMkogQQgiXSRIRQgjhMkkiQgghXCZJRAghhMskiQghhHCZJBEhhBAukyQihBDCZZJEhBBCuEySiBBCCJdJEhFCCOEySSJCCCFcJklECCGEyySJCCGEcJkkESGEEC6TJCKEEMJlkkSEEEK4TJKIEEIIl0kSEUII4TJJIkIIIVwmSUQIIYTLJIkIIYRwmSQRIYQQLpMkIoQQwmWSRIQQQrhMkogQQgiX/X8HrHcdGDL2lAAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.pie(school.values(), labels=school.keys(), autopct='%1.1f%%', shadow=True) # Zeige einen Schatten\n",
|
||
"\n",
|
||
"plt.title(\"Klassenverteilung einer Grundschule\")\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "59e8be26-c070-4205-8260-f4597074ec6f",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-376fc818f2a3d818",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"Zum Herausheben einzelner Kuchenstücke gibt es den Parameter `explode`. \n",
|
||
"\n",
|
||
"Dieser erwartet eine Liste mit Fließkommazahlen zwischen `0.0` (keine Verschiebung) und `1.0` (maximale Verschiebung), die angibt, wie stark jedes Segment vom Mittelpunkt des Pie Charts herausgezogen wird. \n",
|
||
"\n",
|
||
"Beispiel: Das Segment der Klasse 3 wird um 20 % vom Ursprung entfernt:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 56,
|
||
"id": "bf1ea228-1547-4c1d-975e-d7f49111486c",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-e3921561732c3895",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAakAAAGbCAYAAAB+nm/9AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAYspJREFUeJzt3XdYFOfaBvB7dtlG771IURDFRmIJegg27LEb7C16TjQxyZei6WoSYzQejclJ1CRqYi/RxK5RsXdFxYJYAAsiZWlL2TbfH8RVBGRhB2Z2eX7XxaXMzr57zy67z74z77zDsCzLghBCCBEgEd8BCCGEkKpQkSKEECJYVKQIIYQIFhUpQgghgkVFihBCiGBRkSKEECJYVKQIIYQIFhUpQgghgkVFihBCiGBRkaonn3/+ORiG4TtGg/byyy/j5ZdfNvyekpIChmGwYsUK3jJxif7GuLVixQowDIOUlBTO22YYBlOnTuW0zUaNGmHs2LGctikEVKRM8PiP+OzZs+WW5+XloW3btpDL5di9ezdP6SzLzp078fnnn/Mdg9RSaWkpFi9ejI4dO8LJyQlSqRTe3t7o168f1q5dC51Ox3dEIlBUpDiWn5+P7t2749KlS9iyZQt69OjBdySLsHPnTsycOdOkNvbu3Yu9e/dylEh4Pv74YxQXF/Mdo4LMzExERUXhzTffhK2tLT7++GMsWbIEb7zxBlQqFYYPH46vvvqK75hEoKz4DmBJCgoKEBsbi4SEBPzxxx/o2bMn35HMnkqlgo2NDSdtSaVSTtoRKisrK1hZ1f9buqSkBFKpFCJR5d95R40ahQsXLmDz5s0YOHBgudtmzJiBs2fPIikpyaTHIJaLXnGOFBYWokePHjh//jw2b96M3r17V3uf5cuXo3PnznB3d4dMJkN4eDh+/PHHCuudPXsWsbGxcHV1hUKhQGBgIMaPH19unXXr1iEyMhJ2dnawt7dHREQEFi1aVG6d3NxcvPXWW/Dz84NMJkNISAjmzp0LvV5vWOfxcZr58+dj6dKlCA4Ohkwmw4svvogzZ84Y1ps/fz4YhkFqamqFvDNmzIBUKoVSqTQsO3XqFHr06AEHBwdYW1sjOjoax44dK3e/x8dUrl69iuHDh8PJyQkdO3bE2LFj8cMPPwAo25f/+OcxvV6PhQsXolmzZpDL5fDw8MDkyZPLPT5Q8ZhUZapaZ+zYsWjUqFGNn6fHNm7ciPDwcMjlcjRv3hxbtmyp0Obz7Nq1C506dYKNjQ3s7OzQu3dvXLlypdw6lR2TenzsY+vWrWjevDlkMhmaNWtW6W7o+/fvY/z48fDw8DCs9+uvv5ZbJz4+HgzDYN26dfj444/h4+MDa2tr5OfnV5r7xIkT2LNnDyZNmlShQD32wgsvYMSIEUY9RlXH3So7ftSoUSP06dMHR48eNex+DwoKwm+//Vbh/leuXEHnzp2hUCjg6+uLL774otz74jFj3ot6vR6LFi1CREQE5HI53Nzc0KNHjwqHBQBU+7pU9Tdi7PFHY97zQkc9KQ6oVCr07NkTZ86cwaZNm9CnTx+j7vfjjz+iWbNm6NevH6ysrLBt2za8/vrr0Ov1mDJlCgDg0aNH6N69O9zc3DB9+nQ4OjoiJSUFf/zxh6Gdffv2IS4uDl26dMHcuXMBANeuXcOxY8cwbdo0AEBRURGio6Nx//59TJ48Gf7+/jh+/DhmzJiB9PR0LFy4sFy2NWvWoKCgAJMnTwbDMPjmm28wcOBA3L59GxKJBEOHDsX777+PDRs24L333it33w0bNqB79+5wcnICABw4cAA9e/ZEZGQkPvvsM4hEIkOBPnLkCNq2bVvu/kOGDEHjxo3x1VdfgWVZtG7dGg8ePMC+ffvw+++/V3geJ0+ejBUrVmDcuHF48803cefOHXz//fe4cOECjh07BolEYtTrURvVPU8AsGPHDgwbNgwRERGYM2cOlEolJkyYAB8fH6Me4/fff8eYMWMQGxuLuXPnoqioCD/++CM6duyICxcuVFvojh49ij/++AOvv/467Ozs8N1332HQoEFIS0uDi4sLACAjIwPt27c3FDU3Nzfs2rULEyZMQH5+Pt56661ybc6ePRtSqRTvvvsuSktLq+ylbtu2DQAwcuRIo7a1No/xPDdv3sTgwYMxYcIEjBkzBr/++ivGjh2LyMhINGvWDADw8OFDxMTEQKvVYvr06bCxscHSpUuhUCjKtWXMexEAJkyYgBUrVqBnz56YOHEitFotjhw5gpMnT+KFF14wrGfM62KKmr7nBYsltbZ8+XIWABsQEMBKJBJ269atVa772Wefsc8+3UVFRRXWi42NZYOCggy/b9myhQXAnjlzpsq2p02bxtrb27NarbbKdWbPns3a2NiwN27cKLd8+vTprFgsZtPS0liWZdk7d+6wAFgXFxc2JyfHsN6ff/7JAmC3bdtmWNahQwc2MjKyXHunT59mAbC//fYby7Isq9fr2caNG7OxsbGsXq8vt+2BgYFst27dDMseP0dxcXEV8k+ZMqXC88eyLHvkyBEWALt69epyy3fv3l1heXR0NBsdHW34/fG2Ll++vMp1HhszZgwbEBBQ4b7GPE8RERGsr68vW1BQYFgWHx9v+Nt5noKCAtbR0ZF97bXXyi1/+PAh6+DgUG55ZX9jAFipVMrevHnTsOzixYssAHbx4sWGZRMmTGC9vLzYrKyscvd/9dVXWQcHB8Pf6sGDB1kAbFBQUKV/v88aMGAAC4DNzc0tt7y4uJjNzMw0/CiVSsNtz3uMyraRZZ+8F+/cuWNYFhAQwAJgDx8+bFj26NEjViaTsf/3f/9nWPbWW2+xANhTp06VW8/BwaFcm8a8Fw8cOMACYN98880Ktz3992/s6/Ls393znoeAgAB2zJgxht+Nfc8LHe3u40BGRgbkcjn8/PxqdL+nv6nl5eUhKysL0dHRuH37NvLy8gAAjo6OAIDt27dDo9FU2o6joyNUKhX27dtX5WNt3LgRnTp1gpOTE7Kysgw/Xbt2hU6nw+HDh8utP2zYMENPCAA6deoEALh9+3a5dc6dO4dbt24Zlq1fvx4ymQyvvPIKACAhIQHJyckYPnw4srOzDY+rUqnQpUsXHD58uMKuh3//+99Vbkdl2+Xg4IBu3bqV267IyEjY2tri4MGDRrdVG9U9Tw8ePMDly5cxevRo2NraGtaLjo5GREREte3v27cPubm5iIuLK7d9YrEY7dq1M2r7unbtiuDgYMPvLVq0gL29vSEjy7LYvHkz+vbtC5Zlyz1ObGws8vLycP78+XJtjhkzpkJPozKPdwM+ve0A8NNPP8HNzc3w07Fjxwr3NfYxnic8PNzwmgCAm5sbQkNDy/0d79y5E+3bty/Xo3dzcyu3CxIw7r24efNmMAyDzz77rMJtz+6eq+51MVVN3/NCRUWKA0uWLIFUKkWPHj2qPQD8tGPHjqFr166wsbGBo6Mj3Nzc8OGHHwKAoUhFR0dj0KBBmDlzJlxdXfHKK69g+fLlKC0tNbTz+uuvo0mTJujZsyd8fX0xfvz4Cvu2k5OTsXv37nIfDG5ubujatSuAsl0ZT/P39y/3++MP4qeP8wwZMgQikQjr168HUPZht3HjRvTs2RP29vaGxwXKPnCefeyff/4ZpaWlhm19LDAw0OjnMDk5GXl5eXB3d6/QfmFhYYXt4lp1z9PjY3YhISEV7lvZsmc9fv46d+5cYfv27t1r1PY9m/FxzscZMzMzkZubi6VLl1Z4jHHjxgGo+Pdh7GtkZ2cHoOyY7dMGDRqEffv2Yd++fWjRokWl963J30FVqtt2oOw1aty4cYX1QkNDy/1uzHvx1q1b8Pb2hrOzMyfZTFHT97xQ0TEpDoSHh2Pnzp3o0qULunXrhmPHjlXbq7p16xa6dOmCsLAwLFiwAH5+fpBKpdi5cyf++9//GnoXDMNg06ZNOHnyJLZt24Y9e/Zg/Pjx+Pbbb3Hy5EnY2trC3d0dCQkJ2LNnD3bt2oVdu3Zh+fLlGD16NFauXAmg7GBut27d8P7771eap0mTJuV+F4vFla7Hsqzh/97e3ujUqRM2bNiADz/8ECdPnkRaWprhuNjjxwWAefPmoVWrVpW2+ey37Jp8e9br9XB3d8fq1asrvd3Nzc3otoCy5/vpbXysqvN4jHmeTPH4+fv999/h6elZ4XZjRvNVl/HxY4wcORJjxoypdN1nC4mxr1FYWBgAIDExEVFRUYblfn5+hvfI42/6z6rsMaoaLFAfr48x78WaMCZbTbf3aTV9zwsVFSmOtG3bFlu3bkXv3r3RrVs3HDly5LkfkNu2bUNpaSn++uuvct+oqtp90759e7Rv3x5ffvkl1qxZgxEjRmDdunWYOHEigLLh1X379kXfvn2h1+vx+uuvY8mSJfjkk08QEhKC4OBgFBYWGr5FcWXYsGF4/fXXkZSUhPXr18Pa2hp9+/Y13P54d4a9vb1Jj13VmzU4OBh///03oqKiTN41BJR9YFa2u6WyUYzGCAgIAFB2AP9ZlS171uPnz93dnfPX7jE3NzfY2dlBp9Nx/hh9+vTB119/jdWrV5crUrX1uKeam5tr2P0G1P71Acpeo8c91qdVtVfkee/F4OBg7NmzBzk5OUb1pqrj5OSE3NzcCsuN2d66es/XN9rdx6EuXbpg7dq1uHnzJnr06FHlsFzgybeop7815eXlYfny5eXWUyqVFb71Pe6RPN7NkJ2dXe52kUhk+Ob7eJ2hQ4cahgM/Kzc3F1qt1phNrGDQoEEQi8VYu3YtNm7ciD59+pQ7rykyMhLBwcGYP39+hV0+QNmuJmM8bvPZN+zQoUOh0+kwe/bsCvfRarWVvsGfJzg4GNevXy+X6+LFixWGyxvL29sbzZs3x2+//VZu+w8dOoTLly9Xe//Y2FjY29vjq6++qvQ4iLHP3/OIxWIMGjQImzdvRmJiIqePERUVhW7dumHp0qX4888/K12nJr2ax0X76eMpKpXKsMegNnr16oWTJ0/i9OnThmWZmZkVeufGvBcHDRoElmUrPfG8Nr234OBg5OXl4dKlS4Zl6enp2LJlS7X3rav3fH2jnhTHBgwYgGXLlmH8+PHo168fdu/eDblcXmG97t27G3o/kydPRmFhIZYtWwZ3d3ekp6cb1lu5ciX+97//YcCAAQgODkZBQQGWLVsGe3t79OrVCwAwceJE5OTkoHPnzvD19UVqaioWL16MVq1aoWnTpgCA9957D3/99Rf69OljGIKrUqlw+fJlbNq0CSkpKXB1da3x9rq7uyMmJgYLFixAQUEBhg0bVu52kUiEn3/+GT179kSzZs0wbtw4+Pj44P79+zh48CDs7e0Nw5SfJzIyEgDw5ptvIjY2FmKxGK+++iqio6MxefJkzJkzBwkJCejevTskEgmSk5OxceNGLFq0CIMHDzZ6e8aPH48FCxYgNjYWEyZMwKNHj/DTTz+hWbNmz/3S8TxfffUVXnnlFURFRWHcuHFQKpX4/vvv0bx580oL99Ps7e3x448/YtSoUWjTpg1effVVuLm5IS0tDTt27EBUVBS+//77WuV62tdff42DBw+iXbt2eO211xAeHo6cnBycP38ef//9N3Jycmrd9qpVq9CjRw/0798fPXv2RNeuXeHk5ISHDx/i77//xuHDh40+8b179+7w9/fHhAkT8N5770EsFuPXX381PCe18f777+P3339Hjx49MG3aNMMQ9ICAgHLFwZj3YkxMDEaNGoXvvvsOycnJ6NGjB/R6PY4cOYKYmJgaz9f36quv4oMPPsCAAQPw5ptvGk4/aNKkSYXBLM+qq/d8veNhRKHFeDzstbIhqfPnz2cBsH369GE1Gk2lQ0b/+usvtkWLFqxcLmcbNWrEzp07l/3111/LDXs9f/48GxcXx/r7+7MymYx1d3dn+/Tpw549e9bQzqZNm9ju3buz7u7urFQqZf39/dnJkyez6enp5R6voKCAnTFjBhsSEsJKpVLW1dWVfemll9j58+ezarWaZdknQ6vnzZtXYZsAsJ999lmF5cuWLWMBsHZ2dmxxcXGlz9WFCxfYgQMHsi4uLqxMJmMDAgLYoUOHsvv37zes8/g5yszMrHB/rVbLvvHGG6ybmxvLMEyF53Lp0qVsZGQkq1AoWDs7OzYiIoJ9//332QcPHhjWMWYIOsuy7KpVq9igoCBWKpWyrVq1Yvfs2VPlEHRjn6d169axYWFhrEwmY5s3b87+9ddf7KBBg9iwsLBKn69nHTx4kI2NjWUdHBxYuVzOBgcHs2PHji33d1DVEPQpU6ZUaO/Z4cosy7IZGRnslClTWD8/P1YikbCenp5sly5d2KVLl5bLAYDduHGjUbkfKy4uZhcuXMh26NCBtbe3Z62srFhPT0+2T58+7OrVq8udPlHdY5w7d45t166d4W99wYIFVQ5B7927d4X7V3aawaVLl9jo6GhWLpezPj4+7OzZs9lffvmlxu9Fli37W503bx4bFhbGSqVS1s3Nje3Zsyd77tw5wzo1eV327t3LNm/enJVKpWxoaCi7atUqo4ags6xx73mhY1iWoyO8hJAaadWqFdzc3J576gAhDR0dkyKkjmk0mgr7/+Pj43Hx4sVqp2kipKGjnhQhdSwlJQVdu3bFyJEj4e3tjevXr+Onn36Cg4MDEhMTOZkChxBLRQMnCKljTk5OiIyMxM8//4zMzEzY2Nigd+/e+Prrr6lAEVIN6kkRQggRLDomRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEi4oUIYQQwaIiRQghRLCoSBFCCBEsKlKEEEIEy4rvAIRYOpZlkaNSIyO/FNmqUqhKtShS66BS61CsLvt/sVoH1T//Z1lAxDCwEjEQixmIGQZiUdmPlYiB1EoEe7kEDtYSOFlL4WgtgaPiye8SMX33JJaDihQhJirR6HA7U4VbmYW4qyzCo/xSZOSX/PNTisyCUqh1+nrLYyMVw9NBDj9na/g5WcPPWfHPv2U/DgpJvWUhxFQMy7Is3yEIMQf5JRokZxTi1qNC3MwsxM1HZT/3lEXQm9G7yF5uhUauNgj1sEOopx2aetmjqZc9nG2kfEcjpAIqUoRUQqdnkfSwABfuKnEhLRfn05S4k6WCJb9bvB3kaO7jgAgfB0T4OqBNgBPs5dTrIvyiIkUIynpJp2/n4HxaWVG6dC8XKrWO71i8EjFAuLc92ge6oH2QC9oGOVPRIvWOihRpmHRanLuXj0M3snAkOROX7uVBZ0777HjwuGi1+6dodQh2ga2MDmuTukVFijQcRTnAzb+BG7uBm/sxRTILOzJd+U5ltqRWInQIckH3Zh7oFu4Bdzs535GIBaIiRSxbbhqQ+EdZYbp7GmCf7MKL93sdY5M78hjOcjAM0MrPEd3DPRHbzANBbrZ8RyIWgooUsTxqFXD1TyBhDZByFEDlf+J5Hu3QMnVa/WZrIILdbNC7hTcGt/GFv4s133GIGaMiRSwDy5YVpIQ1wLW/AHVh9XcRSdBO9zMeldJggLrCMMCLjZwxONIXvSO8YEPHsEgNUZEi5i3nDnBxbdlPblqN7/6Dx0zMS21cB8HIs6ylYvRo7okhkX5oH+QMhmH4jkTMABUpYn5KC4ErW8p6TWknUNXuPGMk+w1Bt+QB3GUjRvFzVuDVF/0xop0/HK3pJGJSNSpSxHyosoCT/wPO/AyU5HHSpNbOFyGZ33DSFqk5hUSMQZE+GB8VSIMtAKSkpCAwMBAXLlxAq1at+I4jCDQTJRG+3DRgx7vAf5sDR77lrEABgFXBPcQ453DWHqmZYo0Oq06mocuCQ5iw4gyO38ziO1KlDh8+jL59+8Lb2xsMw2Dr1q21aufZ+2o0GsTFxcHHxweJiYnchLUwVKSIcD26BvwxCfiuNXBmGaAtrpOHedX5Rp20S4zHssD+648w/OdT6LXoCDafuwdNPU7KWx2VSoWWLVvihx9+4KzNoqIi9OvXD2fOnMHRo0fRvHlzztq2JFSkiPDcPQ2seRX4Xwfg0npAr63Th3tRe75O2yc1czU9H/+38SK6fHsIm87dE8RMID179sQXX3yBAQO4OX6Zm5uLbt264cGDBzh69CgCAwMrXU+n02HChAkIDAyEQqFAaGgoFi1aVG6d+Ph4tG3bFjY2NnB0dERUVBRSU1MBABcvXkRMTAzs7Oxgb2+PyMhInD171nDfo0ePolOnTlAoFPDz88Obb74JlUrFyTZyhYoUEY7kfcDyXsAv3YAbu2DKgIiacMo6CwdJ3RZCUnNpOUV4d+NFdPvvIfx18QEs5fD5w4cPER0dDQA4dOgQPD09q1xXr9fD19cXGzduxNWrV/Hpp5/iww8/xIYNGwAAWq0W/fv3R3R0NC5duoQTJ05g0qRJhpGTI0aMgK+vL86cOYNz585h+vTpkEjKTrm4desWevTogUGDBuHSpUtYv349jh49iqlTp9bxM1AzNHCC8O/uaWD3dOD+Od4ifOv2JRbfrfzbLBGGME87vN2tCWKbVf2hXh8YhsGWLVvQv3//Wt1XKpUiKCgI586dg7V1+ROdjRk4MXXqVDx8+BCbNm1CTk4OXFxcEB8fbyh8T7O3t8fixYsxZsyYCrdNnDgRYrEYS5YsMSw7evQooqOjoVKpIJcLY5or6kkR/uTdBzZPBH7pzmuBAoAecjpoLXTXHxZg8u/n0O/7ozh8I5PvOLXWp08f3Lhxo1xxeJ4ffvgBkZGRcHNzg62tLZYuXYq0tLJzAp2dnTF27FjExsaib9++WLRoEdLT0w33feeddzBx4kR07doVX3/9NW7dumW47eLFi1ixYgVsbW0NP7GxsdDr9bhz5w63G20CKlKk/mmKgfi5wPcvAJc3or526z1P44JTfEcgRrp0Lw+jfz2NiSvPIC27iO84NTZq1Cj8+uuvePfdd7FgwYLnrrtu3Tq8++67mDBhAvbu3YuEhASMGzcOarXasM7y5ctx4sQJvPTSS1i/fj2aNGmCkydPAgA+//xzXLlyBb1798aBAwcQHh6OLVu2AAAKCwsxefJkJCQkGH4uXryI5ORkBAcH190TUEM0RwmpX4mbgX2fAXl3+U5SjjT3Nto55uNUrj3fUYiR/r72CIeTszCpUxCmxIRAIRXzHcloY8aMgUgkwrhx46DX6/Huu+9Wut6xY8fw0ksv4fXXXzcse7o39Fjr1q3RunVrzJgxAx06dMCaNWvQvn17AECTJk3QpEkTvP3224iLi8Py5csxYMAAtGnTBlevXkVISEjdbCRHqCdF6seDBODXHsCm8YIrUI+NcKWh6OZGrdXj+4M30eXbeGy/9KDOHqewsNDQ2wCAO3fuICEhwbDbDQBmzJiB0aNHG93mqFGjsHLlSkyfPh3z5s2rdJ3GjRvj7Nmz2LNnD27cuIFPPvkEZ86cMdx+584dzJgxAydOnEBqair27t2L5ORkNG3aFMXFxZg6dSri4+ORmpqKY8eO4cyZM2jatCkA4IMPPsDx48cxdepUJCQkIDk5GX/++afgBk5QT4rUrcJHwP6ZZVMYscI576UyHfQJAF7gOwaphQd5JZi65gJWn0zD5/2aIdTTjtP2z549i5iYGMPv77zzDoCyHtGKFSsAAOnp6eWKljFGjBgBkUiEUaNGQa/XY9iwYeVunzx5Mi5cuIBhw4aBYRjExcXh9ddfx65duwAA1tbWuH79OlauXIns7Gx4eXlhypQpmDx5MrRaLbKzszF69GhkZGTA1dUVAwcOxMyZMwEALVq0wKFDh/DRRx+hU6dOYFkWwcHBFTLwjUb3kbpz/jdgz0dAaT7fSYzCSm3QXLUEKh3tYDBnViIG/3k5GG92aQyJmF5Lc0evIOFeYSawNg746w2zKVAAwKhViPO8z3cMYiKtnsXiAzfRd/FRJN7nbgotwg8qUoRb17YB/2sPJO3kO0mt9LG+wncEwpHrDwvQ/4djWLDvhqCmWCI1Q7v7CDdK8oFdHwAX1/CdxCQlzmEIe/Ap3zEIx5p62ePbIS0R7k2jN80NFSliujuHga2vC3bUXk31lSzD5QIbvmMQjknEDKbGNMaUmGBY0bEqs0GvFKk9TQmw+0NgZT+LKVAAMNotme8IpA5odCz++/cNvLr0JB7k1s2M+oR7VKRI7TxIAJZGAyd/gBBmjOBSR+Yi3xFIHTqbqkSv747g76sZfEchRqDdfaTmzq0Adr4H6NTVrmqOWJkDmhT8Dxo9w3cUUsde6xSID3qE0e4/AaNXhhhPpy27Qu62aRZboACAKc3DEI/06lckZm/ZkTsYvuwUHuWX8B2FVIGKFDFOUQ6wakDZFXIbgP621/iOQOrJ6ZQc9PruKE7ezuY7CqkEFSlSvUfXgGUxZaP4GojmxWeqX4lYjKzCUoz8+RTWnKrZtEak7lGRIs93fSfwczdAmcJ3knqlyLqMYGsaAdaQaPUsPtxyGV/uuAq9AC5ZT8pQkSJVOzQPWDccUBfwnaTeMWAxxuM23zEID5YduYN/rzqHYrWO7ygEVKRIZdRFwMZxwMEvYGnDy2viZfElviMQnuy9moEhS44jgwZU8I6KFCkv/wGwvAdw5Q++k/DON/sEGKbhFumGLvF+Pvr/cAxXHtAktXyiIkWeUKaUXZgwnU5mBQBRcRb6u2fyHYPwKD2vBEN/OoH4pEd8R2mwqEiRMtm3gOW9gNxUvpMIyiB7Gore0KnUOkz67Rx2Jz7kO0qDREWKAI+uA8t7Avl0LaVntSw9x3cEIgBqnR5T15zHnwn0HqlvVKQauoeXgRW9gUKax6wytpkX4CMv5TsGEQCtnsXb6xOw7jSdS1WfqEg1ZPfPASv6AEVZfCcRLIbVYYxnCt8xiEDoWWDGlstYfuwO31EaDCpSDVXaSeC3/kBJLt9JBK+L1WW+IxABYVlg5rar+OHgTb6jNAhUpBqiO4eB3wcCpfl8JzELjXJP8B2BCNC8PUlY9Ddde6yuUZH6R3x8PBiGQW5uLt9R6tbNv4HVQwGNiu8kZkNcmI5YV5p8lFT0379v4NejtOuvLgm+SM2ZMwcvvvgi7Ozs4O7ujv79+yMpKalGbaSkpIBhGCQkJBiWFRQUICYmBuHh4bh37x7HqQXqzmFg7XBAS3PS1dRQp5r9zZGGY/aOq9h8roF8hvBA8EXq0KFDmDJlCk6ePIl9+/ZBo9Gge/fuUKlq3xPIzMxETEwMVCoVjhw5Al9fXw4TC9Sja8D6kYCORqrVRqSGhqKTyrEs8MHmS9h7hc6jqguCL1K7d+/G2LFj0axZM7Rs2RIrVqxAWloazp2r3YfG3bt30alTJzg4OODAgQNwcXGpdL3s7GzExcXBx8cH1tbWiIiIwNq1a8uts2nTJkREREChUMDFxQVdu3Y1FM/4+Hi0bdsWNjY2cHR0RFRUFFJTn5wo++eff6JNmzaQy+UICgrCzJkzodVqa7VN1Sp4CKweApTQ9C615ZB5Di5SDd8xiEBp9Symrr2A4zdppCzXBF+knpWXV/ZB6+zsXOP7JiUlISoqCuHh4di5cydsbW2rXLekpASRkZHYsWMHEhMTMWnSJIwaNQqnT58GAKSnpyMuLg7jx4/HtWvXEB8fj4EDB4JlWWi1WvTv3x/R0dG4dOkSTpw4gUmTJoFhyi5HfuTIEYwePRrTpk3D1atXsWTJEqxYsQJffvllLZ6RapQWAKsHA3l3uW+7AWF0aozxpPNjSNXUWj1e++0sLt7N5TuKRWFYljWbGTT1ej369euH3NxcHD161Oj7paSkIDAwEFKpFFFRUdi3bx/EYnG5deLj4xETEwOlUglHR8dK2+nTpw/CwsIwf/58nD9/HpGRkUhJSUFAQEC59XJycuDi4oL4+HhER0dXaKdr167o0qULZsyYYVi2atUqvP/++3jw4IHR21UtnRZYMxS4tZ+7Nhuw637D0CP5Fb5jEIFzspZg479fQoh71V+CifHMqic1ZcoUJCYmYt26dbW6f79+/XDkyBH88Uf1M3zrdDrMnj0bERERcHZ2hq2tLfbs2YO0tLJv0y1btkSXLl0QERGBIUOGYNmyZVAqlQDKenljx45FbGws+vbti0WLFiE9Pd3Q9sWLFzFr1izY2toafl577TWkp6ejqKioVttWqe3TqEBxKDjvJN8RiBlQFmkwceUZ5Bap+Y5iEcymSE2dOhXbt2/HwYMHaz3Q4aOPPsKnn36K4cOHY8OGDc9dd968eVi0aBE++OADHDx4EAkJCYiNjYVaXfaHJxaLsW/fPuzatQvh4eFYvHgxQkNDcedO2XDU5cuX48SJE3jppZewfv16NGnSBCdPln3IFRYWYubMmUhISDD8XL58GcnJyZDL5bXatgri5wIXVnHTFgEASPJT0dGZjuuR6qVkF+H11eeh1en5jmL2BF+kWJbF1KlTsWXLFhw4cACBgYEmtffJJ5/g888/x4gRI7B+/foq1zt27BheeeUVjBw5Ei1btkRQUBBu3LhRbh2GYRAVFYWZM2fiwoULkEql2LJli+H21q1bY8aMGTh+/DiaN2+ONWvWAADatGmDpKQkhISEVPgRiTh4SRLWAPFfmd4OqWCEMw1FJ8Y5fisbn2+7wncMs2fFd4DqTJkyBWvWrMGff/4JOzs7PHxYNszTwcEBCoUCADB69Gj4+Phgzpw5RrX50UcfQSwWY8SIEdDr9YiLi6uwTuPGjbFp0yYcP34cTk5OWLBgATIyMhAeHg4AOHXqFPbv34/u3bvD3d0dp06dQmZmJpo2bYo7d+5g6dKl6NevH7y9vZGUlITk5GSMHj0aAPDpp5+iT58+8Pf3x+DBgyESiXDx4kUkJibiiy++MO0Ju3UQ+OtN09ogVWqruwCgLd8xiJlYdTINoR52GNWhEd9RzJbgi9SPP/4IAHj55ZfLLV++fDnGjh0LAEhLS6txD2T69OkQiUQYNWoUWJaFt7d3uds//vhj3L59G7GxsbC2tsakSZPQv39/w+hCe3t7HD58GAsXLkR+fj4CAgLw7bffomfPnsjIyMD169excuVKZGdnw8vLC1OmTMHkyZMBALGxsdi+fTtmzZqFuXPnQiKRICwsDBMnTqzFM/SUrGRgw2hAT0Ol64pz1hnYWU1AgVbwbx0iEDO3XUWwmy1eCnHlO4pZMqvRfeQ51EXAss5AJl2kr67NdfsKP95txHcMYkYcrSXY+noUGrna8B3F7Aj+mBQx0o53qEDVk15yOs5Aaia3SIPXfjuLYrWO7yhmh4qUJTi3Eri4tvr1CCeaFJ7mOwIxQ8mPCjGTBlLUGBUpc5d+Cdj1Pt8pGhSZMhltHAr5jkHM0Lozd7HtIocn7DcAVKTMWWkhsHEsoC3hO0mDM9KVriNEaufDPy4jLZvDk/YtHBUpc7bzPSDnFt8pGqQo9gLfEYiZKijV4o2156GhE32NQkXKXF3eBFxcw3eKBss9+xQUYjoITmrn4r08fLP7Ot8xzAIVKXOUmwZsf4fvFA0aU1qAoR7p1a9ISBV+PnoHB68/4juG4FGRMjd6HbD5NaCU5pDjWz+bq3xHIGaMZYH3Nl2iiWirQUXK3Bz/DrhLs3ELQXjRGb4jEDOXVViKWdvpy87zUJEyJ8qUstnNiSDIs68izJZGaRHT/HH+PuKTaLdfVahImZMd7wLaYr5TkH8wYDHanUZXEtN9tCURhaVavmMIEhUpc3FlK3BzH98pyDP+JbrIdwRiAe7nFmPuLhrtVxkqUuagtADYPZ3vFKQS3lknIGbofBdiulWnUnH6Tg7fMQSHipQ5OPAFUEDDnYVIVKLEIA86nkBMx7LA9M2XUKKh8++eRkVK6B5cAE4v4zsFeY4BdjT7POHG7SwV/nfwJt8xBIWu3CZkej2w/W2ApW9WQtai5AyAGL5j1Im8ExtQdOMENDn3wFhJIfNpCqfosZC4+BrW0SjToTz4C0rvXQWr00ARGAnnbpMhtnEy7jFObkTuoZWwi+wH566TDMtz9i+DKnE/GIkcjtFjYNvsyXOsun4UqsT9cB/8GXcbKxBLj9zGsLb+8HFU8B1FEKgnJWRnlpX1pIigWWddgr/CMif5LbmbCLs2veE5cj48hs0GdFpkbPgEenXZ9urVJXi04ROAYeAR9xU8R84Dq9fi0eZZYNnqj9WVpt9AQcJuSNwalVtedPMUVNcOwX3obDi9PA45uxdDV1R2Aru+VIXcw7/Buft/ON9eISjR6PE1DaIwoCIlVAUPy45FEcFjWD3GedzhO0ad8Bg6C7YRXSF1C4DUPQguvd+GLj8T6oyyXVKl969Cm/cIrr3ehtStEaRujeDa+22o02+iJPXSc9vWq4uRtW0+XHq8AZHcttxtmuy7kPtFQObVGDbh0WCk1tDmZQAAlAeXw651L1jZu9fNRgvAtosPcC5VyXcMQaAiJVR7PgRK8/lOQYwUY/X8D2RLoS9VAYChqLA6DQCAEUsM6zBiKcAwKL33/Av85ez7EYrgF6Fo1KrCbVK3QKgf3oSupBClD2+C1ZbCyskbJfeuQJ1xC3aRfTnaIuGatf0qWJblOwbvqEgJUfolIPEPvlOQGvBTngDDWPYHCsvqody/DDKfcEj/2T0n8w4DI5FDGb8cek0J9OoSKA/+ArB66Aqr7gmorh6C+uEtOEWPqfR2RVAkbJq9jIcr30b2jv/CtffbEElkyNnzPzjHTkHBhZ24v2wyHq56D+rM1LrYXN5dvJuLLRfu8x2DdzRwQogOfgXAsj/wLI1Y9Qi9XbOxPdOV7yh1Jmfvj1BnpsJzxDeGZWJrB7j1n46cvf9DwbltAMPAJjwaUo9ggGEqbUebn4mc/cvgMWw2GCtplY/n2HEEHDuOMPyee3QN5I1agRGJkXdiPbzH/4Dim6eRvWMBvMYu4m5DBeSb3Uno0dwT1tKG+1HdcLdcqO6fA27s4jsFqYUhjtewPbMT3zHqRM6+H1F86ww8hn8NK/vyhVgR2AY+k3+GrigPjEgMkdwWd78fCWtHz0rbUj+8CX1RLtJXTHuykNWj9O4VFJzfDv93t4ARicvdR5N9F6qrB+E19jsUXtoHuW9ziK0dYB3WCdm7FkFfWgSRzJrz7ebbw/wSLDl0G293a8J3FN5QkRKag1/xnYDUUmv1OQCWVaRYloXy759QdOMEPOLmQFJF4QHKelUAUJx6EXpVHqxD2lW6njygJbzGf19uWfbORZC4+MK+3aAKBYplWWTv+QFOnSdCJFUArB6s/p957h7/a8RIQnP1y9E7GBfVCI7WVfc6LRkdkxKStFPAzb/5TkFqyS7zAjxllnVtoJx9P6LwSjxc+74HkdQaukIldIVK6DWlhnUKL+1D6f3r0CjTUXjlILK2fg27F18pdy5VxroPkX9uGwBAJLM2jAR8/MNIZBDJ7QzHup5WeHEPxAp7Q9GT+TRFSeollN6/jvwzf0Li4l9hdKAlKSzVYsnh23zH4A31pITk4Jd8JyAmYPQajPZMxTepjfmOwpnCCzsBABlrZ5Rb7tLrLdhGdAUAaHLuQ3l4JfTFhbBycIdDh6Gwe7F/ufU1yoeQFdd8tKpOpUTeiQ3wHDnPsEzmHQr7tgPwaNNMiKwd4Nr77Rq3a25WHk/BxI6BcLGV8R2l3jEsjXEUhpSjwIrefKcgJkr2G4xuyQP5jkEs0KR/BeHDXk35jlHvaHefUNCxKIsQmEtXTSZ1Y9XJVChVlrU72RhUpITg1kEg9RjfKQgHrAruIcaZLrdAuFek1uGXo5Y5s8nzUJESAupFWZQ45xt8RyAWauXxFOQVa/iOUa+oSPHt1gHg3mm+UxAOvag9x3cEYqEKSrVYddIyZ9ioChUpvtG1oiyOY+ZZOEm0fMcgFmr1yVTo9A1nvBsVKT7l3QNu7OE7BeEYoyvFKK80vmMQC/UgrwR7rzzkO0a9oSLFp3Mr6IKGFqqH7PkzgBNiiuXHU/iOUG+oSPFFpwHO/8Z3ihqZc6QULy4rhN2cfLjPK0D/dUVIyipfZJeeU+PlFSrYz8kHMzMfuSXG7Zb44bQajRYWQP5FPtr9XIjT98u3+86eEjjPzYfffwuw+lL5A8cbr2jQd22RaRvHsZB8GopO6s7pOzm4lt4wLuVDRYov17YBhRl8p6iRQ6laTHlRipMTbLBvlDU0eqD7qiKo1E8KUZGGRY8QK3zYyfgz49cnavDO3hJ8Fi3D+ck2aOkhRuwqFR6pyuZj25akwZrLGuwdZYNvusoxcVsxsorKbssrYfHRgVL80EvO7caaSJp3B+0cG8aHCOHHygbSm6IixZezv/KdoMZ2j7TB2FZSNHMXo6WnGCtekSMtj8W59Ce9nrfayzC9owztfcXPaam8BSdL8VobCca1liLcTYyf+shhLWHw64WyHtO1LD1ebiTGC95ixEVIYC9jcEdZVhjf31eC/7wggb+D8P6UR7jSUHRSd7Ym3EdukeWf3Cu8d3ZDkJkEpBzhO4XJ8v6ZY9RZUfl1g4yh1rE490CPrkFPppEUMQy6BlnhxL2y4tfSQ4yzD3RQFrM490CHYg2LEGcRjqZpcf6hDm+2E+bs0B30CXxHIBasRKPHujN3+Y5R56hI8cEMe1HP0rMs3tpdgig/MZq7G99relZWEQsdC3jYlC90HjYMHhaW7dKLDbHCyBYSvLisEGP/LMbK/grYSIH/7CjBT70V+PGsBqHfFyLqVxWuPBLOQBTXzFOwEVvuJSQI/9adtvxRpFSk6pu6CEhYy3cKk03ZUYLERzqsG6yol8f7/GU5br5ph8v/scWAphLMOaJG10ArSMTAF4dLcXScNSa2lmD01uJ6yWMMRqPCcM97fMcgFiwluwjn05R8x6hTVKTqW+ImoDSP7xQmmbqzGNuTtTg4xga+9qb9CblaMxAzQIaq/CjADBULT9vK276epcOqyxrM7ixDfIoW/woQw81GhKHNJDifrkdBqXBOdOxjTUPRSd3acv4+3xHqFBWp+mbGu/pYlsXUncXYcl2LA6OtEehk+p+PVMwg0luE/befzNCgZ1nsv61Fh0oGX7Asi8nbS7Cguwy2UgY6PaD5Z4/a4391wqlRCFXRlFekbu24nA6NznJ3K1ORqk85d4AHF/hOUWtTdpZg1SUN1gxUwE5WdszoYaEexZonVeFhoR4JD3W4mVP2prmcoUPCQx1yip+s0+U3Fb4//WRU0jvtZVh2XoOVCWpcy9ThP9tLoNKwGNdKUiHDz+c1cLNm0De07LYofyscuKPFyXta/PdEKcLdRHCU134gB9fkOUmIsFPxHYNYsByVGoeSMvmOUWfoyrz16do2vhOY5MezZUPCX15Z/sTZ5a/IMbZV2Qi7n86qMfPQkwL0rxVFFda5laM3nOcEAMOaS5BZxOLT+FI8LGTRylOE3SOs4fHM7r6MQj2+PFKK4xNsDMva+ojxfx1k6L2mGO42DFb2r59jZDUx2i0Z7xW04jsGsWBbEu6ja7gH3zHqBF2Ztz790h24e4rvFKSepfvEosOtMXzHIBZMZiXC2Y+7wk5ece+DuaPdffWlIAO4S8cnGiLPrJOQiOi7IKk7pVo9dl22zElnqUjVl+vbAdAHVUPElOZhmMcDvmMQC7fjcjrfEeoEFan6cn073wkIj16xvcZ3BGLhTtzORpHa8q5jRkWqPhTnAnfMfxokUnvNis/wHYFYOLVWj6PJWXzH4BwVqfpwYw+g11S/HrFYiqxEBFsLZzYMYpkOXH/EdwTOUZGqD9fNe+g5MR0DFmM9bvEdg1i4g0mPYGkDtqlI1TVNMXBzP98piABEiy/xHYFYuIz8UiTet6zrmFGRqmu3DgAaYV01lvDDN/skGMayvuUS4dl/3bwuplodKlJ17cYevhMQgRAVZ2GAu+VOX0OEwdKOS1GRqmtpJ/lOQARkkD0NRSd16/L9POSoLOeKvVSk6lJRDpBFlxAnT7QsPct3BGLhWBY4k5LDdwzOUJGqS/fOgGaZIE+zyUyAj7yU7xjEwp2lIkWMQrv6yDMYVoexnnf4jkEs3JkUy7laLxWpukQznpNKdLG6zHcEYuGuPMhDiUbHdwxOUJGqKzoNcP883ymIAAXkUg+b1C2NjsWFtFy+Y3CCilRdSb8EaGkaHFKRuDAdsa7ZfMcgFs5SjktRkaord+nbMqnaUKckviMQC3cm1TKOS1GRqis0aII8R6TmHN8RiIW7kKq0iHn8qEjVFboKL3kOh8xzcJPSzPik7hSUanE3x/wPOVCRqgvKFKDQMi/lTLjB6NQY7ZnKdwxi4ZIyCviOYDIqUnUh/SLfCYgZ6C5L5DsCsXBJD81/RnQqUnUhm64bRKoXnEfHLUnduv6QelKkMjlUpEj1rPLT0Mk5l+8YxIIlUZEilcq+zXcCYiaGO9MExKTu3MlSQa3V8x3DJFSk6gL1pIiR2uou8B2BWDCtnsWtzEK+Y5iEihTXSguBQsu6MiapO86Zp2FnpeU7BrFg5r7Lj4oU13JoVx8xHqMtxijPe3zHIBYsJVvFdwSTUJHiGu3qIzXUU3GF7wjEgj3INe8TeqlIcY2Gn5MaCi2gS7qQupOeV8J3BJNQkeIa7e4jNSTNvYk2DuZ93IAI133qSZFyqCdFamGUazLfEYiFSs+lnhR5Gh2TIrXwEpvAdwRioYo1OihVar5j1BoVKS5p1YAqk+8UxAy5Z5+CQmwZl/smwmPOu/yoSHGpJI/vBMRMMaUFGOaRzncMYqHMeYQfFSkulZr/jMOEP/1saCg6qRsZ+eZ7XIqKFJdKcvlOQMxY06IzfEcgFiq/xHxnNaEixSXa3UdMoMi+iqa2RXzHIBaogIoUAQCU0O4+Ypox7jQ6lHCvoETDd4RaoyLFJepJERN1YhL4jkAsEPWkSBkaOEFM5JV9EmLGvK//Q4SHelKkDPWkiIlEJUoM8njEdwxiYagnRcpQkSIcGGh3je8IxMJQkSJlaOAE4UBE8Wm+IxALQ7v7SBnqSREOWGdfRiOF+Z58SYSnVGu+xzmpSHFJY95XwCTCwLB6jPW8w3cMYkH0LMt3hFqjIsUphu8AxEK8LL7IdwRiQfTmW6OoSHGKoaeTcMNPeRIMY8afLERQ9GZcpaz4DmBRqEiZN5EVIJYCYgkgkvzz/8fLpE/d/tRykaRs/cf3e/x/w3JJJW0+vV4lbYqlQJEaO6cvAqujy3cQDiisAcTynaJWqEhxiYrUPxjuP8zro3Awwtldm/vLr8D1q7QDmXBCZG/Pd4RaoyLFpbooUqLKPnjr+Ft8lR/8xhYOMffPQwPC6vVQrlnDdwxiQRiR+X6BpiLFpcixQEhXDguHsL7dk/pReOAANPfv8x2DWBIqUgQAENaL7wTEAuT8vorvCMTSiM23SJlvckIsUEnSDRSdOsV3DGJhRNbWfEeoNSpShAiIctXvfEcgFkhsZ74DJ6hIESIQutxc5G3bzncMYoHE9nZ8R6g1KlKECIRy40awJTRnH+GeyJaKFCHEBKxOB+XatXzHIBZKRD0pQogpCv7eD+2DdL5jEAtFx6QIISbJ+f03viMQC0bHpAghtVZy7RqKz57jOwaxYCLqSRFCaotO3iV1jXpShJBa0SqVyN+xg+8YxMJZubnxHaHWqEgRwqPc9RvAlpbyHYNYOImPD98Rao3m7iMEgJ7VQ6PXQKPTQKvXQqN/8m9l//ew9oC/vb9Jj8lqtVCuW8fRFhBSBZEIEi8vvlPUGhUpwjnDhz2rLfehX9UHv1Zftl51hcGYdSss01Vz+z//17P6Gm3jz91/NrlIFezdC+3Dhya1QUh1rNzdwUgkfMeoNSpSAvb4273RH7ZPFQYNqzGqQFS1TrXtV7GuTq8DC/O9VLUxQhxD0M6rncnt0IAJUh/MeVcf0ICKFMuyKNGV1GiXTlUfyrVdtyYf9lq9FjqWLh0uRMObDje5jeLEKyi+cIGDNIQ8n8THm+8IJmkwRepazjUM2z6M7xjEzDnIHNAnqI/J7Sh/p9nOSf2QeJt3kWowo/vkYjnfEYgFGNh4IBRWCpPa0GZnI3/XLo4SEfJ85r67r8EUKZmVjO8IxMyJGTHiQuNMbke5fj1YtZqDRIRUT0pFyjzIxFSkiGli/GLgZWvaUF5Wo0HuWhp2TuqPNCiI7wgmoSJFiJG4GDCRv3sPtJmZHKQhpHpiJydIPD35jmGSBlOkFFYKMGD4jkHMVKhTKF70fNHkdnLo8vCkHsnCQvmOYLIGU6SsRFZwlDnyHYOYKU6GnV+6hJKLlzhIQ4hx5GFN+Y5gsgZTpADAReHCdwRihpxkTugd1NvkdujkXVLf5E3D+I5gsgZVpFwVrnxHIGZoUJNBJh/T1Dx6hPzduzlKRIhxZGFUpMwKFSlSU1aMFYaFmn4SeO669YBGw0EiQozDyGSQmfnIPoCKFCHP1dm/MzxtTBsdxarVUG7YwFEiQowjCwkBY2X+kwpRkSLkOUY0HWFyG/m7dkGXlcVBGkKMJw83/0ETABUpQqrU1Lkp2ni0MbkdGjBB+KBo1YrvCJygIkVIFbjoRRVduICSxEQO0hBSM9btTL+cjBBQkSKkEs5yZ/QM7GlyOzTbOeGDxNsbUl9fvmNwgooUIZUY3GQwpGKpSW1oMjKQv3cfR4kIMZ5127Z8R+BMgypSDjIHOMgc+I5BBM5KxM2wc+XatYBWy0EiQmrGUnb1AQ2sSAFAsEMw3xGIwHXz7wZ3a3eT2tCr1cjdsJGjRITUjE1b0+eZFIqGV6QcqUiR5xsRzsGw8+07oMvJ4SANITUj8fU1+wsdPo2KFCFPiXCNQEu3lia3Q7OdE75Yt7Oc41EAFSlCyokLM/3Ku0Vnz6L06jUO0hBSczYWdDwKaIBFKsQxhO8IRKBcFa7o0aiHye3QybuEN2IxbDp14jsFpxpckXJVuNIIP1KpIU2GQCKWmNSGJj0dBfv3c5SIkJqxfuEFWDk58R2DUw2uSAE0wo9UJBFJMDR0qMntKNfQsHPCH7uuXfmOwLmGWaTouBR5RmyjWJNP9taXlCB3Iw07JzxhGNh1oyJlEahIkWeNbDrS5Dbytm2DLjfX9DCE1IK8eXNIPE27rIwQNcgiFeZs/lerJNxp4dYCzVybmdyOctVqDtIQUjt23brxHaFONMgiFeEaAanItHnZiOUYEWb6ybuqU6dRmpTEQRpCascSd/UBDbRIScVSNHdtzncMIgDuCnd0a2T6N1AlnbxLeCQNCYYsMJDvGHWiQRYpAIj0iOQ7AhGAoaFDIRGZOOz8/n0UHDjIUSJCas4+1vTz+4SKihRpsKQiKYaEDjG5nZzVawCdjoNEhNQCw8BhwAC+U9SZBlukWru3hpgR8x2D8KhHYA84y51NakNfXIzczZs5SkRIzdl0aA+pr+VMKPusBlukrCXWNMqvgePi8vB5f/4FfV4eB2kIqR2HQYP4jlCnGmyRAoA2Hm34jkB40tq9NcJdwk1uR7ma5ukj/BE7OFjs0PPHGnSRouNSDdfwpsNNbkN14gRKk29ykIaQ2rHv1w8iqWWfTtOwi5R7JBgwfMcg9czD2gNd/U0/p4RmOyd8cxw8mO8Ida5BFylHuSMaOzXmOwapZ6+GvQorkZVJbajv3kVhfDw3gQipBXlEBOShTfiOUecadJECgBi/GL4jkHokE8swuLHp3z6Vq1YDej0HiQipHUcLHzDxWIMvUl38u/AdgdSjXoG94Ch3NKkNfVERcv/4g5tAhNSC2MEBDv368h2jXjT4ItXUpSl8bC33HANSHhfDznO3boW+oICDNITUjuPwOIisrfmOUS8afJECgM7+nfmOQOrBCx4vINQ51KQ2WJaFcvUajhIRUnOMTAbnUaP4jlFvTDt6bCG6+HfB71fNd4JQVZIKWTuzUJxaDG2uFv5v+MM+0t5wu65Eh4yNGcg/nw9doQ5SNylcurrAuXPVsy3kxOcg93guSu6VAAAUjRTwGOwB66An396ydmUhc2cmAMCtlxtcez65aGDRrSI8+O0Bgj8NBiMWxghKLnpRqmPHob51i4M0hNSOw4D+sHI2baYUc0JFCmUndjrLnZFTksN3lFrRl+oh95fD6V9OSFucVuH2h2sfQnVNBd9JvpC6SlF4pRAPfnsAKycr2Le2r6RFQHVdBYd2DvAa4QWRRITMnZlImZeCxl81hsRJgpK7JcjYkoGAtwIAAKn/TYVtc1vI/eRgdSwerHwA77HegilQ3jbenAySyfn9Nw7SEFJLIhFcxo/nO0W9ot19AESMyKxH+dm1sIPHII9yvaenFd0sgmOUI2yb2kLqJoXzy86Q+8lRfLu4yjb9/u0Hly4uUAQoIPOWwWe8D8AChVcLAQCl6aWQ+8phG24L2/Cy4lSaXgqgrIdlE2pTrtfFt2FhwyAWmTZXozo1FarDRzhKREjN2XXrBqm/P98x6hUVqX9Y8ig/6xBrFCQUQKPUgGVZFF4rhDpDDdvmtka3oS/Vg9WxENuUfdDLfGVQZ6ihzlZDnaVG6cNSyHxlKH1UCuURJdwHutfV5tSYwkqBQY1NH66bs2o1wLIcJCKkdlwmTuQ7Qr2j3X3/aO/VHrYSWxRqCvmOwjmvkV54sOIBkt5OAsQAwzDwHucNm1Abo9vI2JgBK0cr2IaXFTa5txwegzyQMi8FAOA52BNybznufHMHnkM9UZhYiEdbH4ERM/Aa4VWjx+Jar8BecJA5mNSGrlCFvC1bOEpESM1Zt2sHRUTDu1grFal/SMQSRPtFY8ftHXxH4VzO3zkoulUE/2n+kLpKoUpSIf33dEgcJbBtVn1vKnN7JvJO5SFweiBE0iedb+fOzuUGXyiPKiGSi2AdYo0b028g+LNgaJQa3P3xLprMawKRhJ+OOyeznW/ZAn2h5X2BIebDdfIkviPwgnb3PWVgyEC+I3BOr9YjY1MGvF71gn1re8j95HDp6gKHtg7I2pVV7f2zdmUhc0cmGr3bCHI/eZXraQu0ePTnI3iP9EbR7SLIPGWQecpg29QWrI6F+qGay80yWjvPdiZPfcWyLJSraJ4+wh/r9u1h89JLfMfgBRWpp7T1aosA+wC+Y3CK1bFgdWzFV1pU9uH7PJk7M/Hor0do9H+NoAhUPHfd9DXpcO3uComzBNCXPW65DHp+juVwMtv54cNQp6ZykIaQ2nF/axrfEXhDu/ueMajxICw4t4DvGDWiK9FBnfGkp6LOUqM4tRhiWzGkLlJYh1rj4fqHYCRM2e6+6yrkHsuFZ5yn4T73lt6DlZMVPIeULcvckYlHWx7Bd7IvJK4SaHI1AACRXASxvPwoucLEsoEYvq/5AgAUgQqUppei4FIBNDkaMCIGMi9ZXT8NFfjY+uBlv5dNbqehzHa+TqnEutxc3NeWvdYhUin+4+KKf9mW7RLekJuLHfl5uFpaCpVej5MhjWEvfv6Iye+zMvG/7OxyywKlUuwIDDL8PvdRBrbk5cFaJMLbbm7oa//k+OHugnz8lZeH//n6cbWZZse2c2coWrXiOwZvqEg945WQV7D4wmJo9Bq+oxit+E4xUuamGH5/uPYhAMAxyhG+r/nC7z9+yNiUgXtL7kGn0kHiIoHHIA84xzw5nqTOVuPpq5bkHMgBq2Vx94e75R7L7RU3eAzwMPyuV+vxYNUD+P3HD4yorAGJswReI71w/+f7YCQMfCf6ljuWVV/iwuIgYkx73NLbd6A6doyjRMLmIbHC225uCPjn+kRb8/Iw9f49bG4UiMYyGUr0enS0sUVHG1v8NyvT6HZDpFL84vdk2PTTHzoHCwuwPT8fP/v5IVWtwccP09HR2gZOVlYo0OmwKDOz3H0bHLEYbg24FwVQkarAWe6Mzv6dsSdlD99RjGbb1BbNV1Q96kfiKIHvRN/nthE0I6jc76HfGjd9kEgqQpOvK14uwDnaGc7R/J0Vr7BSYEDjASa3o1y1qsEMO4+xtSv3+1tubliXq8Sl4mI0lskw+p9ZDk4XqWrUrphh4GZV+UfN7VI12lpbo7lcgeZyBb5+lIF7Gg2crKwwPzMTrzo6wVsiqd0GWQCHAf0hb2L5l+N4HjomVYnBTSz/QmKWrl9wP9hLKz+52Vi6ggLkbd3KTSAzo2NZ7MzPRzHLoqXi+ccjq5OmViP65k10v30L7z14gAeaJ3spQuUyJJaUIE+nw5WSEpSwLPylUpwrKsK10hKMdHIydVPMFmNtDbc33uQ7Bu+oJ1WJdp7t4Gfnh7sFd6tfmQgOAwbDw0wfMJG7eTP0RUUcJDIfN0pLEJeaCjXLwlokwnfePgiR1f54Ygu5Al96eSFQIkWmTov/ZWVjVFoq/goMhI1IjI42tuhrX4yhqSmQMyLM8fSCQiTCrIwMfOXlhXW5uVitVMJJLMbnnp5obEIWc+MydiwkHsI5KZ4v1JOqBMMwGNjY8oajNxTtvdojyDGo+hWfg9XroVyzlqNE5qORVIY/GgViXUAjDHN0xIcP03GztLTW7f3L1hY97OwRKpejo40tfvL1RYFej935Ty51MtXVDXuCgvFnYCC62tlhWXY2OthYwwrAT9lZWOXvj0GODpiR/oCDLTQPVh4ecJnQsOboqwoVqSr0D+lv8iXGCT+4OHm3MP4QNGkVJ+u1dFKGQYBUimZyOd5xc0eoTIbflUrO2rcXi9FIKkWqpvLz5m6XlmJbfh7ecHXD6eIivGBtDWcrK/Sws/9nVKGOsyxC5vHRhxDZ8DdLi5BQkaqCq8IV3QO68x2D1JC/nT/+5fsvk9tRrjLfS7dwiQWgYfWctafS65GmVlc6kIJlWXye8RAfuLvDRiSCngW0/wxaefyvrgGMYbGNiYF9d/rseYyK1HNMjJgIBsK41AQxTlxYHBjGtNes9OZNqI6f4CiR+ViQ+Qhni4pwX6PGjdISLMh8hNNFRejzz3lLmVotrpWUIE1dNvDhRmkprpWUIFf3pHcz7m4aVj/V8/rm0SOc+afNC8VFePP+PYgZBr3tKg5q2ZSXB2exlWGUYWuFAqeKinCxuBgrlTkIlkqrPS/L3DHW1vD85GO+YwgK7c96jsZOjRHjF4MDdw/wHYUYwUZig/4h/U1up6GcvPusHJ0O09MfIFOng51IhCYyGZb5+uGlf3Y7rc9Vljsxd/Tdst2hX3p6YoCDIwDgrloNpU5rWCdDq8G7Dx4gV6+Ds1iMNgoF1voHwPmZnlSWVosl2VlYE/BkxpcWCgXGOjnj3/fuwsXKCl95etXVpguG25QpkHh78x1DUBi2urlxGrgrWVfw6o5X+Y5BjBAXFocP231oUhu6/HwkR78Mtrjqa20RUhdkoaEI3LwJTBXnlDVUtLuvGs1cmyHKO4rvGKQanA0737iJChSpfyIRvGZ+TgWqElSkjDC55WS+I5BqvOTzEho5NDKpjbJh52u4CURIDTgOHdKg5+d7HipSRmjt3hoveLzAdwzyHCPCOBh2fuAANPfvc5CGEONJfHzg/n//x3cMwaIiZaTXWrzGdwRShUb2jdDRp6PJ7TTUAROER2IxvL+ZC7GdXfXrNlBUpIz0kvdLaOHagu8YpBJcDDsvSbqBolOnOEpEiHFcJr0G68hIvmMIGhWpGpjUomFevlnIbCW2nAw7p5N3SX2Tt2wBtylT+I4heFSkaiDaL5qOTQlM/5D+sJZYm9SGLjcXedu2c5SIkOqJrK3hM28ejeYzAhWpGvqg7QcmX0iPcEPEiDgZdq7cuBFsSQkHiQgxjsdHH0Hq34Av5lgD9GlbQ2HOYRgQYvrF9IjpOvl0gp+9aZcVZ3U6KNc2vNnOCX/sYmPhOIiusmAsKlK18EbrN2ArseU7RoM3vKnpvaiCfX9D+yCdgzSEVM/K2wteMz/nO4ZZoSJVCy4KF0xuQSf48inIIQgveb9kcjs5NGCC1BNGLofv4sUQOzryHcWsUJGqpRFNR8DfjvYp84WLY1El166h+Ow5DtIQUj2vL76AolkzvmOYHSpStSQRS/DuC+/yHaNBspPaoW9wX5PboZN3SX1xnjAeDn168x3DLFGRMkGMfwzae7XnO0aDMyBkgMnDzrVKJfJ37OAoESFVs+nYkaY9MgEVKRN98OIHEDOWfSE2IRExIsSFxZncTu76DWBLSzlIREjVJAH+8FnwLRgRfdTWFj1zJgpxCsHoZqP5jtFgRPtGw9fO16Q2WK2Whp2TOieysYHfDz9AbF/xKsTEeFSkODCl1RQ0sm/Ed4wGYURT02c7L9i7F9qMDA7SEFIFkQje38yFLCSE7yRmj4oUB2RiGWZHzaaZKOpYiGMI2nm1M7kdGjBB6prnp5/ArksXvmNYBPpU5Ugr91acHCshVePi5N3ixCsovnCBgzSEVM71zTfg9OqrfMewGFSkODStzTQ6d6qOOMgc0DfI9GHnyt/p5F1Sd5xGjoTb66/zHcOiUJHikMJKgS87fkmj/erAwMYDIbeSm9SGNjsb+bt2cZSIkPLse/eGx0cf8h3D4lCR4lgr91YY33w83zEsipgRIy7U9F2pynXrwKrVHCQipDybjh3h/fUcky++SSoSZJGKj48HwzDIzc3lO0qt/KfVf9DUuSnfMSxGjF8MvGy9TGqD1WiQu249R4kIeULRsiV8v1sERiLhO4pFqlGR+vHHH9GiRQvY29vD3t4eHTp0wK4a7j5JSUkBwzBISEgwLCsoKEBMTAzCw8Nx7969GrUnRBKRBHM6zYFcbNruKVKGiwET+bv3QJuZyUEaQp6QhYXB96cfIbI2bQYUUrUaFSlfX198/fXXOHfuHM6ePYvOnTvjlVdewZUrV2odIDMzEzExMVCpVDhy5Ah8fU07UVMogh2D8XH7j/mOYfZCnULxoueLJrdDs50TrskjIhCwcgWsnJz4jmLRalSk+vbti169eqFx48Zo0qQJvvzyS9ja2uLkyZO1evC7d++iU6dOcHBwwIEDB+Di4lLpetnZ2YiLi4OPjw+sra0RERGBtc/MGLBp0yZERERAoVDAxcUFXbt2hUqlAlC2+7Bt27awsbGBo6MjoqKikJqaarjvn3/+iTZt2kAulyMoKAgzZ86EVqut1TY97ZWQVzC0yVCT22nIuDh5t/jSJZRcvMRBGkLKKNq0gf/yXyF2cOA7isWr9TEpnU6HdevWQaVSoUOHDjW+f1JSEqKiohAeHo6dO3fC1rbqiwiWlJQgMjISO3bsQGJiIiZNmoRRo0bh9OnTAID09HTExcVh/PjxuHbtGuLj4zFw4ECwLAutVov+/fsjOjoaly5dwokTJzBp0iTDAc4jR45g9OjRmDZtGq5evYolS5ZgxYoV+PLLL2v3xDxjetvpaOHWgpO2GhonmRN6BfUyuZ2c36gXRbhj3b49/H9eBvFzPrMIdxiWZdma3OHy5cvo0KEDSkpKYGtrizVr1qBXL+M/SFJSUhAYGAipVIqoqCjs27cPYnH5Idvx8fGIiYmBUqmEYxUXCOvTpw/CwsIwf/58nD9/HpGRkUhJSUFAQEC59XJycuDi4oL4+HhER0dXaKdr167o0qULZsyYYVi2atUqvP/++3jw4IHR2/U8GaoMDN0+FDklOZy011BMjJiIaW2mmdSG5tEj3OzSFdBoOEpFGjKbTp3g+/1iiGQyvqM0GDXuSYWGhiIhIQGnTp3Cf/7zH4wZMwZXr16t8QP369cPR44cwR9//FHtujqdDrNnz0ZERAScnZ1ha2uLPXv2IC0tDQDQsmVLdOnSBRERERgyZAiWLVsGpVIJAHB2dsbYsWMRGxuLvn37YtGiRUhPf3K58IsXL2LWrFmwtbU1/Lz22mtIT09HUVFRjberMh42Hpj3r3l0/lQNWDFWGBY6zOR2ctetpwJFOGHbpQv8fvieClQ9q3GRkkqlCAkJQWRkJObMmYOWLVti0aJFNX7gjz76CJ9++imGDx+ODRs2PHfdefPmYdGiRfjggw9w8OBBJCQkIDY2Fup/znkRi8XYt28fdu3ahfDwcCxevBihoaG4c+cOAGD58uU4ceIEXnrpJaxfvx5NmjQxHEcrLCzEzJkzkZCQYPi5fPkykpOTIZdzNzqvrVdbvNXmLc7as3Sd/TvD08bTpDZYtRrKav62CDGGfa+e8F20EIxUyneUBsfK1Ab0ej1Ka3ldnk8++QQikQgjRowAy7IYNqzyb87Hjh3DK6+8gpEjRxoe88aNGwgPDzeswzAMoqKiEBUVhU8//RQBAQHYsmUL3nnnHQBA69at0bp1a8yYMQMdOnTAmjVr0L59e7Rp0wZJSUkIqYfZisc2H4tLWZewL3VfnT+WueNiwET+rl3QZWVxkIY0ZC6vvQa3d96mE3V5UqMiNWPGDPTs2RP+/v4oKCjAmjVrEB8fjz179hjWGT16NHx8fDBnzhyj2vzoo48gFosxYsQI6PV6xMVVnFmgcePG2LRpE44fPw4nJycsWLAAGRkZhiJ16tQp7N+/H927d4e7uztOnTqFzMxMNG3aFHfu3MHSpUvRr18/eHt7IykpCcnJyRg9uuwaUJ9++in69OkDf39/DB48GCKRCBcvXkRiYiK++OKLmjw9Rvki6gvcyr2F23m3OW/bUjR1boo2Hm1MbodmOycmkUjg9flncBw0iO8kDVqNitSjR48wevRopKenw8HBAS1atMCePXvQrVs3wzppaWkQ1fAqlNOnT4dIJMKoUaPAsiy8vb3L3f7xxx/j9u3biI2NhbW1NSZNmoT+/fsjLy8PAGBvb4/Dhw9j4cKFyM/PR0BAAL799lv07NkTGRkZuH79OlauXIns7Gx4eXlhypQpmDx5MgAgNjYW27dvx6xZszB37lxIJBKEhYVh4sSJNdoGY1lLrPF95+8xctdIGkhRBS56UUXnL6AkMZGDNKQhEjk4wHfRIti0N/3SMMQ0NR7dR7hxNfsqxu8ZD5VGxXcUQXGWO2Pf4H2Qik3b93//nXeQv5MmkyU1J/H3h99PP0EWFMh3FAKBzt3XEIS7hGNhzEJIRDTf19MGNxlscoHSZGQgfy8d9yM1p4iMRKP166hACQgVKR6192qPOZ3m0BV9/2El4mbYuXLtWoCDGUNIw+LwSj/4L/+VpjkSGJNH9xHTxDaKRXZxNuacNm6giSXrFtAN7tbuJrWhV6uRu2EjR4lIQ8DIZPD46EM4DaUpzISIipQADG86HFnFWVh2eRnfUXjFybDzbduhy6EBKcQ40sBA+Cz8L+ShoXxHIVWg/UwC8WabNzGoccMd6hrhGoGWbi1NbidnNQ07J8ax790bgZs2UoESOOpJCcgn7T+BskSJA3cP8B2l3sWFmX7l3aKzZ1F69RoHaYglY2QyeHz4IZyG0e49c0A9KQERi8SYHz0fXfy78B2lXrkqXNGjUQ+T26GTd0l1pI0aodH6dVSgzAgVKYGRiCWYHz0fvQJNv0SFuRjSZAgkYtOG4mvS01Gwfz9HiYglchw6FIGbN0EeFsZ3FFIDtLtPgKxEVpjTaQ4UVgpsTt7Md5w6JRFJMDTU9G+1yjU07JxUzsrLC15fzIZtVBTfUUgtUJESKBEjwmcdPoPcSo7V11bzHafOxDaKhavC1aQ29CUlyN1Iw85JRQ6DB8Fj+nS6QKEZoyIlYAzDYHrb6VBYKfDz5Z/5jlMnRjYdaXIbedu2QZeba3oYYjEkfn7wmjUTNrW4ajgRFipSZmBam2lQWCmw+MJivqNwqoVbCzRzbWZyO8pVltvTJDUkFsN59Gi4vfkGRAoF32kIB6hImYlJLSZBYaXAN2e+4TsKZ0aEmX7yrurUaZQmJXGQhpg7xQuR8JgxA4pmpn/xIcJBRcqMjAofBUeZIz4//jnUejXfcUzirnBHt0bdql+xGspVv3OQhpgziY8P3N97F/Y9TD+NgQgPFSkz0ze4L/zt/THtwDRkl2TzHafWhoYONXkGeM39+yg4cJCjRMTciKyt4TJpEpzHjYVIJuM7DqkjdJ6UGWrp1hLr+qxDU+emfEepFalIiiGhQ0xuJ2f1GkCn4yARMSsMA4f+/RG0exdc/z2ZCpSFoyJlpjxtPLGy50p0CzB9l1l96xHYA85yZ5Pa0BcXI3ezZZ9DRipSvBCJRhs2wPvrOZC4mzZjPh/i4+PBMAxyaTSq0ahImTGFlQLfRn+LyS0m8x2lRriY7Tzvz7+gz8vjIA0xB9Yvvgj/FSvQaNUqKCKa1+ljff3112AYBm+99VaN7peSkgKGYZCQkGBYVlBQgJiYGISHh+PevXvcBm0g6JiUmWMYBlNbT0WIYwg+OfYJSnQlfEd6rtburRHuEm5yO0qa7bxBsO7QHm6vvw7rF1+sl8c7c+YMlixZghYtWpjcVmZmJnr27AmRSIQjR47AxcUFN2/e5CBlw0I9KQvRI7AHVvRcYfJFA+saF70o1YkTKE2mN7sls4mKQsCa1QhYvrzeClRhYSFGjBiBZcuWwcnEq/PevXsXnTp1goODAw4cOAAXF5dK18vOzkZcXBx8fHxgbW2NiIgIrF27ttw6mzZtQkREBBQKBVxcXNC1a1eoVCoAZbsP27ZtCxsbGzg6OiIqKgqpqamG+/75559o06YN5HI5goKCMHPmTGjNbPowKlIWpJlLM2zuuxkxfjF8R6mUp40nJzO85/xGw84tEsPANjoajdavg/8vP8O6TZt6ffgpU6agd+/e6Nq1q0ntJCUlISoqCuHh4di5cydsnzMlU0lJCSIjI7Fjxw4kJiZi0qRJGDVqFE6fPg0ASE9PR1xcHMaPH49r164hPj4eAwcOBMuy0Gq16N+/P6Kjo3Hp0iWcOHECkyZNAsMwAIAjR45g9OjRmDZtGq5evYolS5ZgxYoV+PLLL03avvrGsCzL8h2CcG9D0gbMPzsfxdpivqMYTGszDRMjJprUhvruXdyK7QHo9RylInwTOTjAccAAOMW9CmlAAC8Z1q1bhy+//BJnzpyBXC7Hyy+/jFatWmHhwoVGt5GSkoLAwEBIpVJERUVh3759EIvF5daJj49HTEwMlEolHB0dK22nT58+CAsLw/z583H+/HlERkYiJSUFAc88Nzk5OXBxcUF8fDyio6MrtNO1a1d06dIFM2bMMCxbtWoV3n//fTx48MDo7eIb9aQs1NDQoVjXZx3CnIVxWQKZWIbBjQeb3I7E0xPe876BIjKSg1SET7KmTeE5exYaxx+Ex/QPeCtQd+/exbRp07B69WrI5XKT2+vXrx+OHDmCP/74o9p1dTodZs+ejYiICDg7O8PW1hZ79uxBWloaAKBly5bo0qULIiIiMGTIECxbtgxKpRIA4OzsjLFjxyI2NhZ9+/bFokWLkJ6ebmj74sWLmDVrFmxtbQ0/r732GtLT01FUVGTydtYX6klZOI1Og4XnF+L3q7+DBX8v9YCQAZgVNYvTNkuSkqBcvQb5O3dCX1jIadukjkgksO/eHU4jhtf77ryqbN26FQMGDCjX69HpdGAYBiKRCKWlpRV6RJV53JO6cOECtm3bhlmzZmH16tUYOvTJpWie7Ul9/fXXmD9/PhYuXIiIiAjY2NjgrbfegpWVFbZu3QoAYFkWx48fx969e7FlyxY8fPgQp06dQmBgIADgwoUL2L17N7Zt24bLly9j3759aN++PRQKBWbOnImBAwdWyBoUFASRyDz6KFSkGojj94/jo2MfIas4i5fH39R3E0KdQ+ukbX1JCQoPHEDeX9tQeOwYoNHUyeOQ2pM3awb73r3h0K8vrFxNuzQL1woKCsoNNgCAcePGISwsDB988AGaNzduyPvTRapVq1b48ssv8fnnn2PVqlUYNmwYgIpFqm/fvnB3d8cvv/wCANDr9QgLC0N4eLihSD1Np9MhICAA77zzDt55550Kt3fo0AEvvvgivvvuO0RFRSEsLMzQtrmiIegNxEs+L+GPfn/g02OfIv5efL0+9gseL9RZgQIAkVwO+169YN+rF7RKJfJ37UL+X9tQ/NT5KqT+SQMDYd+7N+x794Lsn2/9QmRnZ1ehENnY2MDFxaXc8tGjR8PHxwdz5swxqt2PPvoIYrEYI0aMgF6vR1xcXIV1GjdujE2bNuH48eNwcnLCggULkJGRgfDwstM0Tp06hf3796N79+5wd3fHqVOnkJmZiaZNm+LOnTtYunQp+vXrB29vbyQlJSE5ORmjR48GAHz66afo06cP/P39MXjwYIhEIly8eBGJiYn44osvavt01TsqUg2Ik9wJi7ssxo7bOzD/7Px661VxMezcWFZOTnAePhzOw4dDnZaGvG3bkL9jJ9S3b9dbhobMyssL9r16wqF3b8jDTT8fTkjS0tJqvIts+vTpEIlEGDVqFFiWhbe3d7nbP/74Y9y+fRuxsbGwtrbGpEmT0L9/f+T9c6K6vb09Dh8+jIULFyI/Px8BAQH49ttv0bNnT2RkZOD69etYuXIlsrOz4eXlhSlTpmDy5LKT+2NjY7F9+3bMmjULc+fOhUQiQVhYGCZONG3wUn2j3X0NVIG6AIsvLMb6pPXQs3U3Us7bxhs7B+6EWFT9Pv26pE5NReGhwyg8dAhFZ86AVZv3LPKCwTCQNQ2DbcdOsH05GorWrQ1DoAnhAhWpBu5K9hXMPjEbV7Kv1En7b0e+jfHNx9dJ27WlLyqC6uQpFB46hMLDh6F9akQUqZ7YyQk2UVGw7dQRNlFRgjvGRCwLFSkCPavHhqQN+O7CdyhQF3DWrsJKgX2D98FB5sBZm3WhJOkGVMePo/j8eRQnJECbmcl3JEFhFAoomjWD9UsdYNupE+TNmoExk5FhxPxRkSIGWcVZ+Pbst9h+ezsn7Q1uMhifdfiMk7bqk/refRQnJJT9XLiAkqQkwMymkqk1hoE0OAiKFi2haNECipYtIGvcGIwVHb4m/KAiRSo4nX4a88/Ox7Wcaya1s6XfFoQ4hXCUij/64mIUX76MksQrKL19C+pbt1F6+7bZz8LOSKWQ+PtBFhgEebNmULRsAXlEBMTPmcaHkPpGRYpUimVZ/J32N3648ANu5d2q8f3bebbDz7E/10Ey4dBmZaH01m2ob99C6a3bKL11E5q0u9BmZgpqYIaVpyekjRpBGtgIssDAf/4fCImPD+22I4JHRYo8l57VY8ftHfjx4o+4W3DX6PstilmEzv6d6zCZsOlyc6HNzKz8J0cJtrgY+tJSsCUlZf8+9TuefUtKJGAkEogkEjBSKZjH/8pkEDs4QOzkBLGTI8ROTrBydoGVuzus3Nxg5e4GKzc3unItMWtUpIhRtHotttzcgiUXlyCjKOO56/rY+mDnwJ0QMfQtvTb0ajVYtQaMxKqsGNGQbtKAUZEiNaLWqbEhaQOWXV6GnJKcStd594V3MabZmHpORgixRFSkSK0UaYqwIWkDVl9fjYeqh4blCisF/h7yN+yl9jymI4RYCipSxCRavRb7Uvfhtyu/ITE7EcNCh+Hj9h/zHYsQYiGoSBHOnM84D3drd/ja+fIdhRBiIahIEUIIESwafkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSwqEgRQggRLCpShBBCBIuKFCGEEMGiIkUIIUSw/h86OUOgF+meGgAAAABJRU5ErkJggg==",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"school = { \n",
|
||
" \"1. Klasse\": 42,\n",
|
||
" \"2. Klasse\": 30,\n",
|
||
" \"3. Klasse\": 26,\n",
|
||
" \"4. Klasse\": 45,\n",
|
||
"}\n",
|
||
"\n",
|
||
"plt.pie(school.values(), labels=school.keys(), autopct='%1.1f%%', explode=[0, 0, 0.2, 0]) # Zeige einen Schatten\n",
|
||
"\n",
|
||
"plt.title(\"Klassenverteilung einer Grundschule\")\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "cbe9aba9-529d-4d4c-87fa-ff46e3a24e5b",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-ed3d080835960776",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"source": [
|
||
"## Aufgabe\n",
|
||
"\n",
|
||
"*5 Punkte*\n",
|
||
"\n",
|
||
"Dir liegt ein Datenset `sec_school` einer Hauptschule vor, das die Klassenstufen von 5 bis 9 auf die Anzahl der Schüler im jeweiligen Jahrgang abbildet. \n",
|
||
"\n",
|
||
"Erstelle einen **Pieplot** und gehe dabei wie folgt vor: \n",
|
||
"1. Wähle ein passendes **Farbschema**, um die einzelnen Klassenstufen anschaulich darzustellen. \n",
|
||
"2. Extrahiere die **Schlüssel** (Klassenstufen) und **Werte** (Anzahl der Schüler) aus dem Datenset und übergebe diese zusammen mit den Farbwerten an `plt.pie()`. Nutze `autopct='%1.1f%%'`, um die Prozentwerte der Segmente anzuzeigen. \n",
|
||
"3. Lasse die 6. Klasse um 25 % und die 9. Klasse um 40 % aus dem Kuchen hervortreten, indem du den Parameter `explode` entsprechend setzt. \n",
|
||
"4. Setze einen geeigneten **Titel** für den Plot. \n",
|
||
"5. Gib den Plot mit `plt.show()` aus, um die Werte zu visualisieren."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 104,
|
||
"id": "5a2e4c2b-051d-4e9d-ae93-0e6fe4b25003",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": false,
|
||
"grade_id": "cell-bf48088c515caf5c",
|
||
"locked": true,
|
||
"schema_version": 3,
|
||
"solution": false,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [],
|
||
"source": [
|
||
"sec_school = {\n",
|
||
" '5. Klasse': 29,\n",
|
||
" '6. Klasse': 35,\n",
|
||
" '7. Klasse': 25,\n",
|
||
" '8. Klasse': 28,\n",
|
||
" '9. Klasse': 31\n",
|
||
"}"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 105,
|
||
"id": "fdebbc40-17eb-48e5-89fa-f8d12ec65688",
|
||
"metadata": {
|
||
"nbgrader": {
|
||
"grade": true,
|
||
"grade_id": "cell-d201bd3e919fcf1c",
|
||
"locked": false,
|
||
"points": 5,
|
||
"schema_version": 3,
|
||
"solution": true,
|
||
"task": false
|
||
}
|
||
},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAeAAAAGbCAYAAAAcMUOXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjguMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/SrBM8AAAACXBIWXMAAA9hAAAPYQGoP6dpAAB6G0lEQVR4nO3dd3hTZfvA8W+SNt2bttBBaQu0jCJDkCkioyDIVBGRJSjvDxSV14Xi3oK+KiqKAxEU2QIiSxFk7z1LoayWtnTvkZzfH5VKbYG2NDlJen+uK5c2OTnPfUKSO8/WKIqiIIQQQgiz0qodgBBCCFEbSQIWQgghVCAJWAghhFCBJGAhhBBCBZKAhRBCCBVIAhZCCCFUIAlYCCGEUIEkYCGEEEIFkoCFEEIIFUgCNrPXXnsNjUajdhi12l133cVdd91V+ndcXBwajYbvv/9etZhqkrzHatb333+PRqMhLi6uxs+t0Wh4/PHHa/ScDRo0YPTo0TV6TmEakoBrwNUP6J49e8rcn5GRQbt27XB0dGTNmjUqRWdbfvvtN1577TW1wxDVVFBQwIwZM+jcuTNeXl7o9XoCAgLo378/8+fPx2AwqB2iEGYjCdhEMjMz6dWrF4cOHWLZsmX07t1b7ZBswm+//cbrr79+S+dYt24d69atq6GILM/UqVPJy8tTO4xykpOT6dSpE5MmTcLV1ZWpU6fy1Vdf8cQTT5CTk8NDDz3EO++8o3aYQpiNndoB2KKsrCyio6M5cOAAS5cupU+fPmqHZPVycnJwcXGpkXPp9foaOY+lsrOzw87O/B/t/Px89Ho9Wm3Fv+tHjBjB/v37WbJkCYMHDy7z2JQpU9izZw8nT568pTKEsCbyLq5h2dnZ9O7dm3379rFkyRL69u170+fMnj2bu+++Gz8/PxwcHGjatCkzZ84sd9yePXuIjo6mTp06ODk5ERoayiOPPFLmmJ9//pk2bdrg5uaGu7s7UVFRfPLJJ2WOSU9P56mnniI4OBgHBwcaNmzI+++/j9FoLD3mar/o9OnTmTVrFuHh4Tg4ONC2bVt2795detz06dPRaDScO3euXLxTpkxBr9eTlpZWet/OnTvp3bs3Hh4eODs707VrV7Zu3VrmeVf7MI8dO8ZDDz2El5cXnTt3ZvTo0Xz++edASd/Z1dtVRqORjz/+mGbNmuHo6Ii/vz/jx48vUz6U7wOuyPWOGT16NA0aNKjy63TVokWLaNq0KY6OjjRv3pxly5aVO+eNrF69mi5duuDi4oKbmxt9+/bl6NGjZY6pqA/4al/jL7/8QvPmzXFwcKBZs2YVdo1cunSJRx55BH9//9LjvvvuuzLHbNy4EY1Gw88//8zUqVMJDAzE2dmZzMzMCuPevn07a9eu5bHHHiuXfK+6/fbbGT58eKXKuF4/d0X9tQ0aNKBfv35s2bKltEsoLCyMH374odzzjx49yt13342TkxNBQUG89dZbZT4XV1Xms2g0Gvnkk0+IiorC0dERX19fevfuXa6rCrjpv8v13iOV7e+vzGdemJ/UgGtQTk4Offr0Yffu3SxevJh+/fpV6nkzZ86kWbNm9O/fHzs7O1auXMmECRMwGo1MnDgRgKSkJHr16oWvry8vvPACnp6exMXFsXTp0tLzrF+/nmHDhtG9e3fef/99AI4fP87WrVt58sknAcjNzaVr165cunSJ8ePHU79+fbZt28aUKVNISEjg448/LhPbTz/9RFZWFuPHj0ej0fDBBx8wePBgzpw5g729PQ888ADPPfccCxcu5Nlnny3z3IULF9KrVy+8vLwA2LBhA3369KFNmza8+uqraLXa0h8fmzdvpl27dmWef//999OoUSPeeecdFEWhVatWxMfHs379eubOnVvudRw/fjzff/89Y8aMYdKkSZw9e5bPPvuM/fv3s3XrVuzt7Sv171EdN3udAFatWsXQoUOJiori3XffJS0tjbFjxxIYGFipMubOncuoUaOIjo7m/fffJzc3l5kzZ9K5c2f2799/0yS+ZcsWli5dyoQJE3Bzc+PTTz9lyJAhnD9/Hh8fHwASExNp3759acL29fVl9erVjB07lszMTJ566qky53zzzTfR6/U888wzFBQUXLd1YeXKlQA8/PDDlbrW6pRxI6dPn+a+++5j7NixjBo1iu+++47Ro0fTpk0bmjVrBsDly5fp1q0bxcXFvPDCC7i4uDBr1iycnJzKnKsyn0WAsWPH8v3339OnTx/GjRtHcXExmzdvZseOHdx+++2lx1Xm3+VWVPUzL8xIEbds9uzZCqCEhIQo9vb2yi+//HLdY1999VXl3y97bm5uueOio6OVsLCw0r+XLVumAMru3buve+4nn3xScXd3V4qLi697zJtvvqm4uLgop06dKnP/Cy+8oOh0OuX8+fOKoijK2bNnFUDx8fFRUlNTS49bvny5AigrV64sva9Dhw5KmzZtypxv165dCqD88MMPiqIoitFoVBo1aqRER0crRqOxzLWHhoYqPXv2LL3v6ms0bNiwcvFPnDix3OunKIqyefNmBVB+/PHHMvevWbOm3P1du3ZVunbtWvr31WudPXv2dY+5atSoUUpISEi551bmdYqKilKCgoKUrKys0vs2btxY+t65kaysLMXT01N59NFHy9x/+fJlxcPDo8z9Fb3HAEWv1yunT58uve/gwYMKoMyYMaP0vrFjxyr16tVTrly5Uub5Dz74oOLh4VH6Xv3zzz8VQAkLC6vw/ftvgwYNUgAlPT29zP15eXlKcnJy6S0tLa30sRuVUdE1Kso/n8WzZ8+W3hcSEqIAyl9//VV6X1JSkuLg4KD897//Lb3vqaeeUgBl586dZY7z8PAoc87KfBY3bNigAMqkSZPKPXbt+7+y/y7/ft/d6HUICQlRRo0aVfp3ZT/zwvykCboGJSYm4ujoSHBwcJWed+0v7IyMDK5cuULXrl05c+YMGRkZAHh6egLw66+/UlRUVOF5PD09ycnJYf369dcta9GiRXTp0gUvLy+uXLlSeuvRowcGg4G//vqrzPFDhw4trcECdOnSBYAzZ86UOWbv3r3ExsaW3rdgwQIcHBwYMGAAAAcOHCAmJoaHHnqIlJSU0nJzcnLo3r07f/31V7nmsP/85z/XvY6KrsvDw4OePXuWua42bdrg6urKn3/+WelzVcfNXqf4+HgOHz7MyJEjcXV1LT2ua9euREVF3fT869evJz09nWHDhpW5Pp1Oxx133FGp6+vRowfh4eGlf7do0QJ3d/fSGBVFYcmSJdx7770oilKmnOjoaDIyMti3b1+Zc44aNapcDbEiV5umr712gC+//BJfX9/SW+fOncs9t7Jl3EjTpk1L/00AfH19iYiIKPM+/u2332jfvn2ZlhhfX98yzeJQuc/ikiVL0Gg0vPrqq+Ue+3eT8c3+XW5VVT/zwnwkAdegr776Cr1eT+/evW86mORaW7dupUePHri4uODp6Ymvry8vvvgiQGkC7tq1K0OGDOH111+nTp06DBgwgNmzZ1NQUFB6ngkTJtC4cWP69OlDUFAQjzzySLm+pJiYGNasWVPmS8/X15cePXoAJc1r16pfv36Zv68mmWv7Ve+//360Wi0LFiwASr7IFy1aRJ8+fXB3dy8tF0q+TP9d9jfffENBQUHptV4VGhpa6dcwJiaGjIwM/Pz8yp0/Ozu73HXVtJu9Tlf7yBs2bFjuuRXd929XX7+777673PWtW7euUtf37xivxnk1xuTkZNLT05k1a1a5MsaMGQOUf39U9t/Izc0NKBkjca0hQ4awfv161q9fT4sWLSp8blXeB9dzs2uHkn+jRo0alTsuIiKizN+V+SzGxsYSEBCAt7d3jcR2K6r6mRfmI33ANahp06b89ttvdO/enZ49e7J169ab1oZjY2Pp3r07kZGRfPTRRwQHB6PX6/ntt9/43//+V1or1Gg0LF68mB07drBy5UrWrl3LI488wocffsiOHTtwdXXFz8+PAwcOsHbtWlavXs3q1auZPXs2I0eOZM6cOUDJwJCePXvy3HPPVRhP48aNy/yt0+kqPE5RlNL/DwgIoEuXLixcuJAXX3yRHTt2cP78+dJ+6KvlAkybNo2WLVtWeM5/146qUusxGo34+fnx448/Vvi4r69vpc8FJa/3tdd41fXmqVbmdboVV1+/uXPnUrdu3XKPV2bU881ivFrGww8/zKhRoyo89t9JsrL/RpGRkQAcOXKETp06ld4fHBxc+hm5WkP7t4rKuN7AI3P8+1Tms1gVlYmtqtd7rap+5oX5SAKuYe3ateOXX36hb9++9OzZk82bN9/wy3/lypUUFBSwYsWKMr+Er9ek2L59e9q3b8/bb7/NTz/9xPDhw/n5558ZN24cUDLF5t577+Xee+/FaDQyYcIEvvrqK15++WUaNmxIeHg42dnZpb9+a8rQoUOZMGECJ0+eZMGCBTg7O3PvvfeWPn61ic3d3f2Wyr7eF1F4eDi///47nTp1uuXmSihJBhU1AVY02rsyQkJCgJLBQP9W0X3/dvX18/Pzq/F/u6t8fX1xc3PDYDDUeBn9+vXjvffe48cffyyTgKvragtDenp6aZMwVP/fB0r+ja62NFzreq1ZN/oshoeHs3btWlJTUytVC74ZLy8v0tPTy91fmes11Wde3DppgjaB7t27M3/+fE6fPk3v3r2vOzUD/vn1e+2v3YyMDGbPnl3muLS0tHK/1q/WJK82faWkpJR5XKvVltZYrh7zwAMPlE4J+bf09HSKi4src4nlDBkyBJ1Ox/z581m0aBH9+vUrM2+3TZs2hIeHM3369HLNkFDS/FkZV8/57y+jBx54AIPBwJtvvlnuOcXFxRV+ed1IeHg4J06cKBPXwYMHy02ZqqyAgACaN2/ODz/8UOb6N23axOHDh2/6/OjoaNzd3XnnnXcq7Hes7Ot3IzqdjiFDhrBkyRKOHDlSo2V06tSJnj17MmvWLJYvX17hMVWpjV79QXJt/2VOTk5pS0913HPPPezYsYNdu3aV3pecnFyuVaUyn8UhQ4agKEqFi8ZUp9YdHh5ORkYGhw4dKr0vISGBZcuW3fS5pvrMi1snNWATGTRoEF9//TWPPPII/fv3Z82aNTg6OpY7rlevXqW11vHjx5Odnc3XX3+Nn58fCQkJpcfNmTOHL774gkGDBhEeHk5WVhZff/017u7u3HPPPQCMGzeO1NRU7r77boKCgjh37hwzZsygZcuWNGnSBIBnn32WFStW0K9fv9JpGDk5ORw+fJjFixcTFxdHnTp1qny9fn5+dOvWjY8++oisrCyGDh1a5nGtVss333xDnz59aNasGWPGjCEwMJBLly7x559/4u7uXjpV5UbatGkDwKRJk4iOjkan0/Hggw/StWtXxo8fz7vvvsuBAwfo1asX9vb2xMTEsGjRIj755BPuu+++Sl/PI488wkcffUR0dDRjx44lKSmJL7/8kmbNmt3wB9WNvPPOOwwYMIBOnToxZswY0tLS+Oyzz2jevHmFP0qu5e7uzsyZMxkxYgStW7fmwQcfxNfXl/Pnz7Nq1So6derEZ599Vq24rvXee+/x559/cscdd/Doo4/StGlTUlNT2bdvH7///jupqanVPve8efPo3bs3AwcOpE+fPvTo0QMvLy8uX77M77//zl9//VXpRWt69epF/fr1GTt2LM8++yw6nY7vvvuu9DWpjueee465c+fSu3dvnnzyydJpSCEhIWUSX2U+i926dWPEiBF8+umnxMTE0Lt3b4xGI5s3b6Zbt25VXv/5wQcf5Pnnn2fQoEFMmjSpdApa48aNyw2M+zdTfeZFDVBh5LXNuTr1oaJpCdOnT1cApV+/fkpRUVGF0wZWrFihtGjRQnF0dFQaNGigvP/++8p3331XZurDvn37lGHDhin169dXHBwcFD8/P6Vfv37Knj17Ss+zePFipVevXoqfn5+i1+uV+vXrK+PHj1cSEhLKlJeVlaVMmTJFadiwoaLX65U6deooHTt2VKZPn64UFhYqivLP9Jpp06aVuyZAefXVV8vd//XXXyuA4ubmpuTl5VX4Wu3fv18ZPHiw4uPjozg4OCghISHKAw88oPzxxx+lx1x9jZKTk8s9v7i4WHniiScUX19fRaPRlHstZ82apbRp00ZxcnJS3NzclKioKOW5555T4uPjS4+pzDQkRVGUefPmKWFhYYper1datmyprF279rrTkCr7Ov38889KZGSk4uDgoDRv3lxZsWKFMmTIECUyMrLC1+vf/vzzTyU6Olrx8PBQHB0dlfDwcGX06NFl3gfXm4Y0ceLEcuf795QVRVGUxMREZeLEiUpwcLBib2+v1K1bV+nevbsya9asMnEAyqJFiyoV91V5eXnKxx9/rHTo0EFxd3dX7OzslLp16yr9+vVTfvzxxzJT6G5Wxt69e5U77rij9L3+0UcfXXcaUt++fcs9v6KpZocOHVK6du2qODo6KoGBgcqbb76pfPvtt1X+LCpKyXt12rRpSmRkpKLX6xVfX1+lT58+yt69e0uPqcq/y7p165TmzZsrer1eiYiIUObNm1epaUiKUrnPvDA/jaLU0CgRIUS1tGzZEl9f3xtOHxNC2B7pAxbCTIqKisr1t23cuJGDBw/edGlMIYTtkRqwEGYSFxdHjx49ePjhhwkICODEiRN8+eWXeHh4cOTIkRpZdlAIYT1kEJaNi4uLIzQ0lP379193/q0wDy8vL9q0acM333xDcnIyLi4u9O3bl/fee0+SrxC1kDRBq+jSpUs8/PDD+Pj44OTkRFRUVIU7pdyIRqPhl19+Kf27qKiIYcOGERgYWOFUEqEeDw8PFixYwMWLFykoKCA1NZVFixaVWYZQCFF7SA1YJWlpaXTq1Ilu3bqxevVqfH19iYmJKbOecFXl5uYyZMgQYmJi2LJlC6GhoWW2ZRNCCGE5pAaskvfff5/g4GBmz55Nu3btCA0NpVevXtWuDaWnp9OzZ0/i4+NLk29FDAYDY8eOJTQ0FCcnJyIiIsrtF7xx40batWtXujZ1p06dSlfcOXjwIN26dSvdb7hNmzZlau1btmyhS5cuODk5ERwczKRJk8jJyanWNQkhhC2TBKySFStWcPvtt3P//ffj5+dHq1at+Prrr6t1rsuXL9O1a1egZGWlitYKvspoNBIUFMSiRYs4duwYr7zyCi+++CILFy4ESlaNGjhwIF27duXQoUNs376dxx57rHQJyOHDhxMUFMTu3bvZu3cvL7zwQul+t7GxsfTu3ZshQ4Zw6NAhFixYwJYtW6q86IAQQtQGMgpaJVdXxZo8eTL3338/u3fv5sknn+TLL7+87kL4FdFoNOj1esLCwti7dy/Ozs5lHq/MIKzHH3+cy5cvs3jxYlJTU/Hx8WHjxo2lSf1a7u7uzJgxo8IYx40bh06n46uvviq9b8uWLXTt2pWcnJwKVwITQohaS81VQGoze3t7pUOHDmXue+KJJ5T27dtX6TyAMnjwYEWr1SofffRRucevrtS0f//+0vs+++wzpXXr1kqdOnUUFxcXxd7eXmnbtm3p46NHj1YcHByUfv36KR9//HGZVaReffVVxc7OTunevbvy7rvvltlI/Pbbb1f0er3i4uJSenN2dlYA5dixY1W6LiGEsHUyCEsl9erVo2nTpmXua9KkCUuWLKnyuUaMGEH//v155JFHUBSFyZMnX/fYn3/+mWeeeYYPP/yQDh064ObmxrRp09i5c2fpMbNnz2bSpEmsWbOGBQsWMHXqVNavX0/79u157bXXeOihh1i1ahWrV6/m1Vdf5eeff2bQoEFkZ2czfvx4Jk2aVK7civY8tVpGA2RegswEKMqB4gIozoei/JL/Xv273H//vml04OgODu7g6FHy/44e4ODxr7/dQe9883iEEFZJErBKOnXqVG6bs1OnTpVuW1dVo0aNQqvVMmbMGIxGI88880yFx23dupWOHTsyYcKE0vtiY2PLHdeqVStatWrFlClT6NChAz/99BPt27cHSvYPbdy4MU8//TTDhg1j9uzZDBo0iNatW3Ps2LFKbTBv0YwGyLgIGRcg/fy/bucgMx6MZtpBRmv/d0L2BK8Q8GkEda7eGoN7gHniEELUOEnAKnn66afp2LEj77zzDg888AC7du1i1qxZzJo1q/SYKVOmcOnSJX744YdKnXPEiBFotVpGjRqFoig8++yz5Y5p1KgRP/zwA2vXriU0NJS5c+eye/fu0lHTZ8+eZdasWfTv35+AgABOnjxJTEwMI0eOJC8vj2effZb77ruP0NBQLl68yO7duxkyZAgAzz//PO3bt+fxxx9n3LhxuLi4cOzYMdavX18jO/XUuMJciN8HF/dA8sl/kmyWGRPszRiLIDel5JYaC7Ebyj6udwWfhv8kZJ+Gf/83HOxvfV9kIYTpSAJWSdu2bVm2bBlTpkzhjTfeIDQ0lI8//pjhw4eXHpOQkFDlrdWGDx+OVqtlxIgRGI3GctsCjh8/nv379zN06FA0Gg3Dhg1jwoQJrF69GgBnZ2dOnDjBnDlzSElJoV69ekycOJHx48dTXFxMSkoKI0eOJDExkTp16jB48ODSPU9btGjBpk2beOmll+jSpQuKohAeHl4uBtWkxMLF3SW3C7sg6ZjlJNrqKsyGhAMlt2tptOARBP7NIaQTNOgMdVuAViY+CGEpZBS0sE0FWXBp79/Jdjdc2lNSi6zNHD0hpGNJMm7QGfyjJCELoSJJwMI2FBfC2U1wcjWc3wHJx0Exqh2VZXP0/Kd23KAz1I2Cv+d7CyFMTxKwsF6FuXB6PRxfCafWQUGG2hFZNyevkoQceidE9gOPQLUjEsKmSQIW1iUvHU6tKUm6p/+A4jy1I7JRGghqC80GQbOBMtpaCBOQBCwsX3YSnPi1JOme3VwyMliYkQaC7yhJxq1HytxkIWqIJGBhmXJS4NACOLYcLu6S/lxL4OgJz8SAnV7tSISwCTINSViW8ztg97cliddQoHY04lpNB0jyFaIGSQIW6ivIgoM/w57ZkHRU7WjE9UTdr3YEQtgUScBCPSmxsOOLkuRbmK12NOJG3ANLpioJIWqMJGBhfmc3w/bPIWat9O1ai+aDZY6wEDVMErAwD0MRHFkKOz6HhINqRyOqSpqfhahxkoCFaSkKHFoIf75VstGBsD51IqDebWpHIYTNkQQsTOf0H/D7q3D5sNqRiFshtV8hTEISsKh58QdKEu+ZjWpHImpC1H1qRyCETZIELGpOWhxseAsOLwZkfRebENQWvEPVjkIImyQJWNy6nBT4axrs+RYMhWpHI2pS1ANqRyCEzZIELKqvMLdkHu/WT6AgU+1oRE3T2pWs/yyEMAlJwKJ69v8IG96ErAS1IxGmEnYXuPqqHYUQNksSsKiajIuw4gmI3aB2JMLUZPSzECYlCVhU3r4fYO1L0txcG9g5QWQ/taMQwqZJAhY3l3EJVk6C07+rHYkwl4g+4OCqdhRC2DRJwOLG9s+DNS9CQYbakQhzkuZnIUxOErCoWGY8rHwSYtapHYkwNycvaNRT7SiEsHmSgEV5B36CNS9AvtR6a6WmA0Bnr3YUQtg8ScDiH5kJ8OtTcGqN2pEINcniG0KYhSRgUeLUOlj6KOSnqx2JUJN7EIR0VDsKIWoFScACNn9UsqiGYlQ7EqG2qCGg0agdhRC1giTg2qwoD5ZPhCNL1I5EWAoZ/SyE2UgCrq0yLsLPD0HCQbUjEZbCtwnUjVI7CiFqDUnAtdG5bbBwJOQkqx2JsCSy768QZiUJuLbZ8x389hwYi9SORFgaaX4WwqwkAdcWhiL47VnYO1vtSIQlCr4DvELUjkKIWkUScG2QcwUWjIDz29SORFgqqf0KYXaSgG1dwqGSwVYZF9SORFgqrR00G6R2FELUOpKAbdn5nfDjfbJ9oLixsG7gUkftKISodSQB26pz2+DH+6EwW+1IhKVrIUtPCqEGrdoBCBM4+xfMu0+Sr7g5e2eI7Kt2FELUSlIDtjWxG2D+Q1Ccp3YkwhpE3AN6F7WjEKJWkhqwLYlZD/OHSfIVlWem0c85BcUYjYpZyhLCWkgN2FacXA0LR4GhQO1IhLVw8oaG3c1S1KcbYli+P54BLQMY0iaIxv5uZilXCEumURRFfpZau+MrYdEYWd1KVM3tj0C//5m8GEVR6PTeBuIz8kvvaxbgzuDWQQxpHYins97kMQhhiSQBW7sjS0v28TUWqx2JsDZjVptl79+dZ1IYOmtHhY852msZ3DqIsZ1DCfd1NXksQlgSScDW7NAiWDYeFIPakQhr4xEMTx02y96/U5YeZv6u8zc8RqOBbhF+jO0cSqeGMidZ1A7SB2ytjiyBZY+BYlQ7EmGNmg8xS/ItMhhZfSThpscpCmw4kcSGE0lE1nVjbOdQBrQMRG8n40SF7ZIasDW6sAu+7ycDrkT1/d828G9m8mJ+P5bIuB/2VOu5vm4OjGgfwsPtQ/B2kX5iYXskAVubtHPwTXfZy1dUn19TmLDdLEU9/tM+fj108xrwjTjYabmvTRCTujfC392xhiITQn3SvmNN8jPgpwck+YpbY8a5v38cT7rl8xQUG/lx53m6TvuT99ecIDNfRvsL2yAJ2FoYimHRaEg+oXYkwqppIOo+s5S09uhl8opqboBgfpGRmRtjufODP/n6rzMUFMvgQ2HdJAFbi9XPlSwzKcStCL4DPOubpajlB+JNct703CLe/u04d0/fxKI9F2SFLWG1JAFbgx0zYc+3akchbEEL8zQ/X8kuYOvpKyYt41J6Hs8uPkSfTzbzx/FEk5YlhClIArZ0J9fA2hfVjkLYAq09NBtslqJWHUqg2Ew105OJWYyds4cHvtzO/vNpZilTiJogCdiSXT4MS8bKXF9RM8LvBmdvsxT1y4FLZinnWrviUhk8cxsv/3KE7AJZGU5YPknAliorEX56UPb0FTXHTKOfz6fksv98ulnK+jdFgbk7ztHro01sOCHN0sKySQK2REV5MP9ByLyodiTCVti7QOQ9ZilquQq133+Lz8jnke/38MT8/aRky4I1wjJJArZE66ZC/D61oxC2JPIe0LuYpajlB00z+rk6Vh6Mp8dHm1i8V37MCssjCdjSxKyH3d+oHYWwNVEPmKWYo/EZnE6yrG6TtNwinll0kBHf7uRCaq7a4QhRShKwJclJgeUT1Y5C2Bpnn5IBWGZgqrm/NWFzzBWiP/6LbzafkbnDwiJIArYkKydBtgwcETWs6UDQmX7jM6NRYaUFNT9XJLfQwFurjvPwtztJzpK+YaEuScCWYt9cOPGr2lGo6t3NBbT9Ohu3dzPxm5bFwJ9zOXml7HKD41fmEf5pFk5vZ+I7LYsBP+dy4srNlyQ8nmyg//xcPN7LxOWdTNp+nc35jH+md01em4/3+5kE/y+LHw+VXWt40dEi7p1vxU2XLczT/LzzbCoJGflmKetWbYtN4Z5PN7M9NkXtUEQtJgnYEqSegTUvqB2F6jadK2ZiWz07xrqwfoQzRUboNS+XnMJ/mgvbBOiYPcCJ4xNdWfuwM4oCvebmYrhBk2JsqpHOs3OJrKNl4ygXDv3HlZfvdMDx70rhypNF/HS4iHUjXPighyPjVuZxJbckOWfkK7y0oYDP77HSXXg865csP2kGKw6qP/q5KpKzCnj42518tiEG2RROqEG2I1Sb0QDf9YaLu9SOxOIk5xjxm57NptHO3BlScRPqoUQDt32Zw+knXAn3rvj35IOLc7HXaZg7yKnCxz/YWsC+BAM/3+cMgP/0LH4d5kzbQB3jV+YRWUfL0x0cauaizK3zZOjxqsmLKSw20vbt38nIs86diro29uV/Q1vKvsPCrKQGrLbNH0nyvY6Mv7vovJ00FT6eU6gwe38RoZ4agj0qPsaoKKyKKaaxt5boeTn4Tcvijm+y+eXEP4niNn8de+INpOUp7I03kFek0NBby5bzxey7bGDSHVb8pWym5ueNJ5OsNvkCbDqVTN9PN7MnLlXtUEQtIglYTZf2wqb31I7CIhkVhafW5NMpWEdzP12Zx77YXYjrO5m4vpvF6tPFrB/hgl5XcQJOylHILoT3thbQO9yOdSOcGRRpz+AFeWyKK1muMLqhHQ+3sKft19mMXp7HnIFOuOjh/1bl82VfJ2buKSLis2w6fZfD0SQr2gLPvzn4NTFLUZY8+rmyEjLyeXDWDr7aFCtN0sIspAlaLYW58FUXSDmtdiQW6f9+zWP16WK2POJCkHvZ34kZ+QpJOUYSshWmbyvkUpaRrY+44GhXPgnHZxkJ/CibYc3t+GmIc+n9/efn4qKH+dfcd63XNxaQnq8wppU9vebmcvj/XPj1VDGf7S5k72OuNXuxptLjNej8tMmLyS4o5va31pNfZDtrlvdo4seHD7TEw8le7VCEDZMasFrWvSTJ9zoe/y2PX2OK+XNU+eQL4OGooZGPjjtD7Fj8gBMnrhhZdrzixffrOGuw00JT37K16CZ1tJzPqPi354krBuYdLuLNux3YGFfMnSE6fF20PNDMnn0JRrIKrOE3qwaa32eWktYcuWxTyRfg9+NJ3P/lNuLT89QORdgwScBqOLcd9nyndhQWR1EUHv8tj2Unitkw0plQr5u/PRWl5FZgqDgp6nUa2gboOJlSNkGcSjUSUkG/saIojP81n496OeCq12AwwtXccvW/1ynKstTvAJ7BZinKEtZ+NoVTidkM/mIbxxMy1Q5F2ChJwOamKDLl6Dom/pbPvENF/DTYCTcHDZezjVzONpJXVJLxzqQZeXdzAXvjDZzPMLLtQjH3L8rDyV7DPY3+GSUd+Vk2y47/MyDo2Y56Fhwp4uu9hZxONfLZrkJWnixmQtvyg6u+2VeEr7OGeyNKmh471bdjw9lidlws5n/bC2jqq8XTseL+ZosSZZ7ab3JWAdtseC7t5cx8HvhyO1tPX1E7FGGDTL88jijrwE+QcEDtKCzSzD0lSfOuOWUXvZg9wJHRLfU42sHm8wY+3llIWp6Cv6uGO0N0bHvEGT+Xf35LnkwxknFNM/GgJvZ82U/h3S2FTFqTT4SPliUPONG5ftm3f2K2kbc3F7Bt7D+bFrQL1PHfDg70/SkPPxcNcwZWPJXJomjtodkgsxT166H4G87BtgVZBcWMnr2LD+5rwaBWQWqHI2yIDMIyp8Ic+LQ1ZF9WOxJhyxr3hocWmKWogZ9v5cCFdLOUpTaNBp7pFcHEbg3VDkXYCGmCNqct/5PkK0wv6n6zFHMuJafWJF8o6T2atvYkU385bPO1fmEekoDNJf0CbPtM7SiErdO7QsQ9ZinKFub+Vse8HecZP3cveYVWNCdcWCRJwOby+6tQLFMahIlF9gV9xXOba5qtjn6ujN+PJ/LwtzvJKah4+psQlSEJ2Bwu7IIjS9SOQtQGZmp+PnIpg9jkHLOUZan2nktjzPe7pSYsqk0SsKnJtCNhLs51IKybWYr6ZX/trf1ea9fZVB79YQ/5RZKERdVJAja1QwtK1nwWwtSaDQKd6WcWGo0KKw/Vzv7fimw5fYUJP+6jsNi2VgMTpicJ2JQKc+H319WOQtQWZmp+3nEmhcTMArOUZS02nEjiifn7KDZIEhaVJwnYlLZ+DFlSUxBm4BkC9e8wS1G1dfTzzaw9mshTCw7IFCVRaZKATSU3VaYdCfMx09KTBcUGVh9JMEtZ1ujXQwk8u+ggRknCohIkAZvKrllQVLtHiQozinrALMX8eSKZzHyZenMjS/df4qVfDtvMnsIbN25Eo9GQnp6udig2RxKwKRTmwM4v1Y5C1Bb+UeAXaZaiVhyU0c+VMX/XBd5addykZbz22mtoNJoyt8jIqr0P4uLi0Gg0HDhwoPS+rKwsunXrRtOmTbl48WINRy2uJZsxmMLe7yEvTe0oRG3RwjyDr7Lyi/jjeJJZyrIF3245S7ivKw/dUd9kZTRr1ozff/+99G87u1v7Sk9OTqZPnz5otVo2b96Mj48Pp0/LvuWmIjXgmlZcCNs/VzsKUWtooLl5+n/XHLlMgUy1qZJXVxxhuwm3a7Szs6Nu3bqltzp16lT7XBcuXKBLly54eHiwYcMGfHx8KjwuJSWFYcOGERgYiLOzM1FRUcyfP7/MMYsXLyYqKgonJyd8fHzo0aMHOTklXXIbN26kXbt2uLi44OnpSadOnTh37lzpc5cvX07r1q1xdHQkLCyM119/neJi2+z2kARc0w4tgExpphNmEtIJPALNUpSMfq66IoPChB/3cj4l9+YHV0NMTAwBAQGEhYUxfPhwzp8/X63znDx5kk6dOtG0aVN+++03XF1dr3tsfn4+bdq0YdWqVRw5coTHHnuMESNGsGvXLgASEhIYNmwYjzzyCMePH2fjxo0MHjwYRVEoLi5m4MCBdO3alUOHDrF9+3Yee+wxNJqSPbY3b97MyJEjefLJJzl27BhfffUV33//PW+//Xa1rsvSyXaENe3IEvjjDUiLUzsSURv0+xhuH2PyYpKy8unw7gaZYlNNjfxcWTqhI26O9jV2ztWrV5OdnU1ERAQJCQm8/vrrXLp0iSNHjuDm5lapc8TFxREaGoper6dTp06sX78enU5X5piNGzfSrVs30tLS8PT0rPA8/fr1IzIykunTp7Nv3z7atGlDXFwcISEhZY5LTU3Fx8eHjRs30rVr13Ln6dGjB927d2fKlCml982bN4/nnnuO+Hjb+wEoNeCa1nwIPLEP7p8DgberHY2wZTo9NB1glqJWHkyQ5HsLYpKymTR/f41OT+rTpw/3338/LVq0IDo6mt9++4309HQWLlxY5XP179+fzZs3s3Tp0pseazAYePPNN4mKisLb2xtXV1fWrl1bWvu+7bbb6N69O1FRUdx///18/fXXpKWVjInx9vZm9OjRREdHc++99/LJJ5+QkPDPtLaDBw/yxhtv4OrqWnp79NFHSUhIIDfXNK0IapIEbApaHTQbCI/+AWPWQGQ/0MhLLWpYwx7g7G2WolbU4p2PasqfJ5N5d7XpRkZ7enrSuHHjag2aeumll3jllVd46KGHbprAp02bxieffMLzzz/Pn3/+yYEDB4iOjqawsBAAnU7H+vXrWb16NU2bNmXGjBlERERw9uxZAGbPns327dvp2LEjCxYsoHHjxuzYsQOA7OxsXn/9dQ4cOFB6O3z4MDExMTg6Olb5uiydjII2tZAOJbeUWNj+GRyYL9sSipphpsU3zl7J4eDFDLOUZeu+3nyWRn5uPNA2uMbPnZ2dTWxsLCNGjKjW819++WW0Wi3Dhw9HURSGDh1a4XFbt25lwIABPPzwwwAYjUZOnTpF06ZNS4/RaDR06tSJTp068corrxASEsKyZcuYPHkyAK1ataJVq1ZMmTKFDh068NNPP9G+fXtat27NyZMnadiwYbWuwdpIAjYXn3Do9z/oNhV2fwO7v4acZLWjEtZK7wYR95ilqNq8768pTP3lCKG+LrRtcGutF8888wz33nsvISEhxMfH8+qrr6LT6Rg2bFjpMSNHjiQwMJB33323Uud86aWX0Ol0DB8+HKPRWOZcVzVq1IjFixezbds2vLy8+Oijj0hMTCxNwDt37uSPP/6gV69e+Pn5sXPnTpKTk2nSpAlnz55l1qxZ9O/fn4CAAE6ePElMTAwjR44E4JVXXqFfv37Ur1+f++67D61Wy8GDBzly5AhvvfXWLb1elkgSsLm5+MBdz0OnJ+Hg/JIpSykxakclrE1kX7B3MktRK2T0c40qNBj5v3l7+e3JLvi5Vb9Z9eLFiwwbNoyUlBR8fX3p3LkzO3bswNfXt/SY8+fPo9VWrfvrhRdeQKvVMmLECBRFISAgoMzjU6dO5cyZM0RHR+Ps7Mxjjz3GwIEDycgoaSVxd3fnr7/+4uOPPyYzM5OQkBA+/PBD+vTpQ2JiIidOnGDOnDmkpKRQr149Jk6cyPjx4wGIjo7m119/5Y033uD999/H3t6eyMhIxo0bV+3XyZLJKGi1KQqcWgPbZsC5rWpHI6zFw0tK+oBN7NDFdPp/Ju9LU+jSqA4/PNKudAqOqH1kZJDaNBqI6ANjfoNHN5Ts6arR3fx5ovZy8YWwbmYpSub+ms7mmCt8uemM2mEIFUkCtiSBbeD+72HSfrjj/0B//cnwohZrNrhkpL2JGY0KKw9KAjalj9af5MCFdLXDECqRBGyJvEKgz3vw9FHo8Rq41VM7ImFJosyz9vP2MykkZRWYpazaqsigMGn+frILbHOpRXFjkoAtmZMndH4anjoMA2eCXzO1IxJq82oAwW3NUtQv+2X0szmcT83l9RVH1Q5DqEASsDXQ2UPLh2DCNnh4qdn6/4QFMlPtt6DYwJqjl81SloBFey+y/lii2mEIM5MEbG0adoeRv8B/tsJtw0Bbc2vLCisQ9YBZitlwPImsfGkWNacpSw+Rki1N/rWJJGBrVbc5DPoSnjpUMqfYwUPtiISp1W0Bvo3NUpSMfja/K9mFvLjssNphCDOSBGzt3AOg5xsw+ShEvwseptv8W6jMTM3PmflFbDiZZJayRFlrjyaybP9FtcMQZiIJ2FY4uEGHCfDkARjyLQS0UjsiUZM0WrOt/bzm8GUKi41mKUuU9/aq42TmF6kdhjADScC2Rqsr+aJ+bCOMXgWNewOy0o7VC+lU0tphBssPyuhnNV3JLuSjdafUDkOYgSRgW9agMzy0ACbugtYjQeegdkSiuszU/JyUmc/22BSzlCWub+6OcxxPyFQ7DGFikoBrA9/G0H9GycIedz4HTubZQ1bUEJ0emg4wS1ErDsZTg3vGi2oyGBVeXS5zg22dJODaxNUX7n4JJh+Dvh+Cd7jaEYnKaNizZFEWM5DRz5ZjV1yqDMiycZKAayN7J2g7Dh7fA0PnQfAdakckbqSFeZqfzyRnc/hShlnKEpXz7m8nZJlKGyYJuDbTaqHJvTB2HYz9HZr0LxltKyyH3g0a9zFLUb9I7dfiJGUV8PF6GZBlq+TbVpQIbgtD58ITe6HdY2DvonZEAkp+INlXf9P2qlhxQEY/W6Lvt8VxKjFL7TCECUgCFmV5h8E90+DpI3D3VHD1Vzui2s1Mc38PXEgnLiXXLGWJqik2Kryy/IjaYQgTkAQsKubsDXc+W7ITU//PwDdS7YhqHxc/CLvLLEUtl9qvRdtxJpXVhxPUDkPUMEnA4sbsHKD1CJiwAx5aBKF3qh1R7dF8cMnCKiZmMCr8eki+3C3dJ3/EoCgyR8yWSAIWlaPRQONeMGoljP+rZGEIrZ3aUdk2M+18tC32CslZsguPpTtxOYs1R2SLSFsiCVhUXb3bYMg38ORB6PA4OLirHZHt8Q6DoDZmKeqX/TL62VpILdi2SAIW1ecRBNFvl6yw1fNNcA9UOyLbYaalJ/OLDKw7KrUqa3HichZrjyaqHYaoIZKAxa1zdIdOk+DJQzD465J9a8WtMVMC3nAiiSxZ6MGqfCq1YJshCVjUHJ0dtHgA/rMZRi6Hhj3Ujsg61bsN6jQyS1G/7JfRz9bmWEIm645JLdgWSAIWphF2Fzy8pGT0dMuHSzYUEJVjpsFXGXlFbDyVbJayRM369I8YtUMQNUASsDAtvyYw8POS+cRd/gtOXmpHZNk0Wmg+xCxFrT6cQGGx0SxliZp1ND6T9VILtnqSgIV5uNWF7q+UDNjq8wF4NVA7IsvUoDO41zNLUbLzkXX75A9ZI9raSQK2ENvit/HrmV8pNtr4gBi9C9wxHp7YB/fPgcDb1Y7Isphp8NXljHx2nk0xS1nCNI5cyuTPE0lqhyFugSRgC/HZ/s+YsnkKfZb2Yc7ROWQXZqsdkmlpddBsIDz6B4xZA5H9ZCcmnQM0HWCWolYejMcoA2mt3g/b49QOQdyCWv6NZxkOJB3g8JXDAFzOucz0PdPpubgn03dP53JOLZijGdIBHvyxZH/i2x8BOye1I1JHo57g6GGWon6RtZ9twqZTyVxMk000rJUkYAsw7/i8cvdlF2Uz59gc+iztwwubX+BE6gkVIjMzn3Do97+SfuK7XgQXX7UjMq8W5hn9fDopm6PxmWYpS5iWUYGfd11QOwxRTRpFZnSr6nLOZXov6Y1BMdz02Dvq3sGoZqPoEtTFDJFZgKJ8ODgftn8OKTY+7cLBA545ZZa9fz9cd5IZG06bvBxhHn5uDmx74W7sdFKfsjaymr7KlsUsq1TyBdh5eSc7L++koWdDRjYdSb+wftjr7E0coYrsHeH2MdBmNJxaA9tmwLmtakdlGk36mSX5Aqw4qO7o5/wLR8jcuYTCxFgM2an4DnoJ58YdSh835KSRtvF78uP2Y8zPwSG4Gd49xmPvfeOlTo352aT9NZe8U9sw5Gdh5+6Hd/dHcQpvC0D20T9J3zQHpTAPl6geeHd/tPS5xRmJJC54mXqjPkbr4GyaCzeRpKwC1h9LpE+UeUbPi5ojP5lUpCgKK2JXVPl5p9NP88q2V4heEs3Xh74moyDDBNFZEI0GIvrAmN/g0Q3QbBBoTL9Nn1mZafTz/vNpnEtRt89QKczH3i8M757/Kf+YopC09C2K0y/jO3gq9UZ/gp27H4kLpmIszL/+OQ1FJC54GUNGInUGTiHw0a/w6f0EOjcfAAy5GaSumYFXt0fwG/omOcc2knt6V+nzU9Z9gVfX0VaXfK/6ced5tUMQ1SAJWEV7E/dyMftitZ+fnJfMp/s/pefinryz8x0uZNWCvqDANnD/9zBpP9zxf6B3VTuiW+fqD6FdzVKUJcz9dQq/Ha87R+DcuGO5x4rT4imMP4l3rwk41GuMvU8Q3tETUIoLyTm+6brnzD60HmN+Fr6Dp+IY1BQ7D38c60eh9wsrOW/6ZTQOzrg0uROHeo1xrN+CopSSz0vOsU1otHY4R5SPx1psjb3CuZQctcMQVSQJWEXLY5fXyHnyivOYf2I+9y67l8kbJ3Mo+VCNnNeieYVAn/dKBmz1eA3crLj5rfkQ0Jr+o2gwKvx6KMHk5dwKxVAEgMbun6VLNRotGp09BRePXfd5uad34hAQSer6mVyY8TDx304gY/tCFGNJ946ddyBKUUFJs3deFoUJp9D7NsCQn0365nkV1satiaLAT1ILtjqSgFWSW5TLurh1NXpOg2Jg/bn1DP9tOCNXj+SP839gVGx8qUEnT+j8dMlSlwNngl8ztSOquqj7zFLMltNXuJJdYJayqsveOwiduy/pm+ZgyM9GMRSRsWMxhqwrGLJTr/u84vREck5uRTEa8bv/NTw6PkjmrmVkbFsAgM7RlTp9n+bKrx9x+YfJuDS/G6ewNqRt+Ba31v0ozkgkfvYk4r+dQM6JLea63Bq1eO9FWVrUysggLJX8cf4PcotN1xe3P2k/+5P2E+IewogmIxjQcACOduYZ5KMKnT20fKjkdvqPkgFbZ/5UO6qb8w4vaVY3g+VWMPdXo7PDd9BLpKz+hIufPAgaLY4NWuIY1gZuNF9DMaJz9sSn9+NotDoc6jbEkJVC5q6leHZ+CADnxh3LNHvnnz9MUXIc3j3HEz/rMerc+yw6Fy8SfpiMY3BzdC6epr3YGpaSU8jqIwkMaCn7clsLScAqWX66Zpqfb+Zc5jne2vkWnx/4nKGRQ3kw4kF8nHzMUrZqGnYvuV0+Ats/g8OLwVikdlQVM9Pgq/wiA+usZCN3h7oNCRgzA2NBDoqhGJ2zBwk/TEZf9/pbNOpcvdFodWi0/wzOs/cJxpCThmIoQvOv2QJKcRGp62bi028yxWkJKEYDjvWjSp7nHUhBwkmcG95hmgs0oWX7L0kCtiLSBK2ChOwEdl3edfMDa1BaQRpfHvyS6CXRvLbtNc5mnDVr+aqo2xwGfQlPHYJOT5bMtbU0Zlp84/fjiWQXWNc641oHF3TOHhSlXqLw8mmcG10/IToENqEoLQHlmi6XorRLJYm5gql6Gdt+xjGsNQ51G4JiBOM/UwEVYzEYrbMpd9vpFLLyLfTHpihHErAKlscuR7lhe5rpFBgKWBKzhAG/DOCJP55g9+XdqsRhVu4B0PMNmHwUot8Fj/pqR1QioFXJ6l9m8Mt+9Uc/X2UszKMw8QyFiWeAkjm4hYlnKM4s2Vgg58QW8s8foij9MrkxO0hc8DLOjdrjFNq69BxXfv2QtE3fl/7t1uoejPlZpP0+i6LUS+TG7iZj+yLcWvUtV37hlfPknNiMZ+eHAbDzDgKNlqyD68iN3U1RykX09a5f27ZkhQYjG2SDBqshTdAqWBu3Vu0QUFDYeHEjGy9upLlPc0Y1G0XPkJ7otDY2v/ZaDm7QYULJbkxHl5U0T8fvVy8eMzU/Z+QW8depZLOUVRmFl2NInP9i6d9pG74BwKV5d+r0fRpDdippG77BkJOOztUL12Z349HpwTLnKM5MLrN5h527L/4PvEHqH9+Q9d3j2Ln54H57f9zvKLu3sqIopK75DK+7x6HVl4yJ0No74HPPU6Sun4liKMK753+wc6tjqss3uXVHE6UZ2krIUpRmdin7Er2X9FY7jAoFugYyvMlwhjQagrO9dS5IUGVxW0oGbJ1ay41H+dQwjRYmHy/ZJ9nEftp5nheXHTZ5OcIyuOh17H25J472Nvxj2kZIE7SZbbywUe0QrutS9iU+2P0BPRb34H97/0dSbi1oymrQGR5aABN3QeuRJVsCmqXcLmZJvmAdo59FzckpNLAl5oraYYhKkARsZn9d/EvtEG4qqzCL7458R/SSaF7a8hKn0k6pHZLp+TaG/jNKFva48zlw8jZteWYafJWQkceuuOvPnxW2ae3RWrCNqQ2QJmgzyinKocvPXSiy1CkxN9AxoCOjmo6iY6D1LtdXJUV5cOBH2P4FpMbW7LntHOGZGHB0r9nzVuCrTbG8u7oWbGUpyvB20bP7pR7otBq1QxE3IDVgM9oWv80qky+UxD7+9/EMWTGEFbErrPY6Ks3eCdqOg8f3wNB5EFyDc0Ib9TJL8gXLWPtZmF9qTiE7z6aoHYa4CUnAZmTJ/b+VdSrtFC9teYneS3rz7eFvySrMUjsk09Jqocm9MHYdjP0dmvQvM/q2Wsw0+jkmMYtjCZlmKUtYHmtZeKU2kyZoMzEqRrot7EZqvm31x7nYuzCo4SBGNB1BgGuA2uGYR+oZ2DET9v8IRVXcgcbRo6T52c70g72mrz3JZ3+eNnk5wjIFeDiybUp3tcMQNyA1YDM5lHzI5pIvlPRrzzs+j3uW3sOzm57l6JWjaodket5hcM80ePoI3D21ZDvBympyr1mSL8DygzL6uTaLz8gnNjlb7TDEDUgCNpPNlzarHYJJGRQDa+LW8OCqBxm9ZjQbL2zE5htXnL3hzmdLdmLq/xn4Rt78OWZqft57Lo0LqXlmKUtYrj0yAt6iSQI2k/1JKq64ZGZ7E/fyxIYnGLB8AItPLabQUKh2SKZl5wCtR8CEHfDQIgi9s+Lj3OpBg+s8VsNk7q8A2B2XpnYI4gYkAZtBsbGYI1eOqB2G2Z3NOMvr21+n5+KezDw4k/T8dLVDMi2NBhr3glErYfxfJbVd7TWrvTYbXDKoy8SKDUZWHUoweTnC8u2WGrBFkwRsBidST5BXXHubA1PzU/niwBf0XNyTN7e/ybnMc2qHZHr1boMh38CTB6HD4+DgDi3M0/y8+fQVUnJsvNVBVMq5lFySsvLVDkNchyRgMziQdEDtECxCviGfhacW0v+X/jy54cna0SzvEQTRb8PkYyW7H5nBCpn7K66xR5qhLZYkYDOoFYmmCoyKkQ0XNjBy9UiG/zacdXHrMCrWuf9qpTm4maWYvEID62QZQnGNXWelGdpSSQI2A6kBX9+h5EP8d9N/6bu0Lz8d/4ncoly1Q7Jq648nklNouPmBotbYc04SsKWSBGxil7IvkZRXC3YVukUXsy/y7q536bWkF5/u+5QrebKbS3WskNHP4l+OJ2SRXVCsdhiiApKATUxqv1WTUZDB14e/JnpxNK9sfYXY9BreCMGGpecWsulUstphCAtjMCrsOyf9wJZIErCJSf9v9RQaC1l2ehmDlg/i/37/P3Ym7FQ7JIu36nACRQYbX/xEVIssyGGZ7G5+iLgVJ1JlK7hboaCw5dIWtlzaQhPvJoxsNpLeDXpjp5W37r8t3y+jn0XFjiXY+KYpVkpqwCZ2JuOM2iHYjOOpx5myeQp9lvZhztE5ZBfKOrdXXUrPY7cMthHXcUbWhLZIkoBN6EreFdvfrk8Fl3MuM33PdHou7sn03dO5nCPTblYciMfWl94W1Xc+NZcig41P9bNCkoBN6Ey61H5NKbsomznH5tBnSR+e/+t5jqccVzsk1cjaz+JGio0K51KquHWmMDlJwCYkzc/mUawU89vZ33jg1wcYt3Ycf138y/Z3YrrGyctZnLgsLS3ixk4nSQK2NDKSxYRkCo357by8k52Xd9LQsyEjm46kX1g/7HX2aodlUlL7FZVx5or0A1saqQGb0NmMs2qHUGudTj/NK9teodeSXsw6NIuMggy1QzIJRVFYcVBGP4ubi5UasMWRBGxC0gStvit5V5ixfwY9F/fknZ3vcCHrgtoh1ai959K4mFZ7d9oSlRcrI6EtjiRgE8kqzCI5T1YlshR5xXnMPzGffsv6MXnjZA4lH1I7pBqxXHY+EpUkU5EsjyRgE4nLiFM7BFEBo2Jk/bn1DP9tOCNXj+SPc39Y7U5MxQYjqw4nqB2GsBKZ+cWyN7CFkUFYJpKYm6h2COIm9iftZ3/SfkLcQxjRZAQDGg7A0c5R7bAqbXPMFVJzCtUOQ1iRM8k5+LlZz3vc1kkN2ERkNx/rcS7zHG/tfItei3vx2f7PSMlLUTukSvlFRj+LKpLxApZFErCJSAK2PmkFaXx16Cuil0Tz2rbXLHoQXW5hMeuPSSuLqJo0aTGxKJKATSQl3zpqUaK8AkMBS2KWMPCXgTz+x+Psvrxb7ZDKWX8skdxCg9phCCuTmisJ2JJIH7CJSA3Y+ikobLq4iU0XN9HMpxmjmo2iV0gvdFqd2qHJ6GdRLVIDtixSAzYRa+lHFJVzNOUoz/31HH2X9WXusbnkFuWqFktqTiF/nZIpbqLqZNCeZZEEbCJSA7ZNl7Iv8cHuD+ixuAcf7f2IpNwks8ew6nACxcbas9a1qDlp0gRtUSQBm4jUgG1bVmEWs4/MJnpJNC9teYmTqSfNVvYKGf0sqklqwJZFErAJZBZmUmiUN3ptUGwsZkXsCu5beR+PrXuMbZe2mbS8i2m57DmXZtIyhO1Kzy1SOwRxDRmEZQLp+elqhyBUsD1hO9sTttPYqzEjm47knrB7sNfW7E5MKw7GU4t2WhQ1LD2vCEVR0Gg0aocikBqwSRQYCtQOQajoVNoppm6dSu8lvfn28LdkFmbW2LmX75fRz6L6DEaFjDypBVsKScAmIM3PAiApN4mP931Mz0U9eX/X+8Rn31ryPHE5k5OJWTUUnaitpB/YckgCNoEig/zCFP/ILc5l3vF53LP0Hp7Z9AxHrxyt1nl+kdqvqAFSA7YckoBNoNAgvzBFeQbFwNq4tTy46kFGrxnNxgsbUSrZoasoCisPSgIWt67IIIMILIUMwjIBaYIWN7M3cS97E/cS6hHKiKYj6B/eHwedw3WP3x2XxqV0WUhf3DqDzCG3GFIDNgGpAYvKOptxlje2v0Gvxb2YeWAmafkVTzFaLnN/RQ0xyjB6iyEJ2ASkBiyqKjU/lS8OfkGvxb14c/ubnMs8V/pYkcHIb4cTVIxO2BJZRc1ySBO0CcggLFFd+YZ8Fp5ayOKYxdwVdBejmo0iLTWQNFlAQdQQoyRgiyEJ2ASkCVrcKqNiZMOFDWTEHucZ+/tZ+fgDaockbERIHWe1QxB/kwQshIV6PKkFXeefwCFsHaGjH1U7HCFEDZMEbAIOdtcfzSrEzXgojkzbE4Hn73tRgPxjxzBkZqJzd1c7NCFEDZJBWCbgZOekdgjCSnXKD+abBd54/r73nzuNRnJ37VIvKCGESUgCNgEnnSRgUXXPXmrJUzMTUM6eL/dYzvYdKkQkhDAlaYI2AUc7R7VDuKGckzlc+e0KeefyKE4vpv4T9XFvU7Z5Mz8+n8SFieSczEExKDgGOhL8eDB6H32F51SKFZJXJZO2JY3itGIc6jngf78/bi3cSo9J35bO5cWXMeYb8eriRb1h9UofK0wuJG56HOGvhaNz0pnmwi1UHaML07aH4fLXHq43PjVnhyRgIWyNJGATsPQEbCww4ljfEa87vTg/o3xtqyCpgLNvn8XrTi/8BvmhddJScKkArf31G0wSlyaSvi2dwDGBONRzIOtIFudnnCdsahhOIU4UZxVzafYlgsYFYe9rz7n/ncOliQvuLUsSf/zcePzv9691ybd7XgP+szgX5eL+Gx5XGBtLUVIS9n5+ZopMCGFqkoBNwNITsFsLtzI1039LWpyEawtX6g6tW3qfg9+NB5alb0vHt58vbreVnNfnbh9yjuZwZc0VgscHU5hciM5Jh8cdHgC4NHGhIL4AWkL6jnQ0Og0et3vc+sVZkVfOtaL5ogMoRZWb45u7cyce995r4qiEEOYifcAm4GxnvfPsFKNC1qEsHOo6EDc9juNPHCf2jVgy9954T1ulSEFjX3aTb41eQ+6pXAAc/B0wFhpLmr2zi8k7m4djsCOGHANJS5Oo93C9ik5rk+oZ3Jj7ZxOa/7QbKpl8QZqhhbA1UgM2AUedZdeAb6Q4sxhjvpHkVcn4D/HH/35/sg9nc/6z84Q+H4pLpEuFz3ONciVlbQouES7o/fTkHMspSdrGksd1LjqCHg3i4tcXUQoVPDt64hblxsVvL+Ld3ZuiK0Wc/+Q8ikHBb6AfHm1tszbcP7sRIxamoCQervJzc2UglhA2RRKwCTjZW/Eo6L9HAbm3dqdOdB0AnEKcyD2dS+qfqddNwPUeqsel2ZeImRIDGtD76fHq7EXa5n82F3Bv415msFfOiRwKLhYQ8HAAp54/RfB/grHzsCP2jVhcIlywc7edt6cODW/GtqLhkr0oBkO1zlEUH0/h+fPo69ev4eiEEGqwyG+4jRs30q1bN9LS0vD09FQ7nCpz0DngqHMk35CvdihVpnPTgQ4cAsr2+ToEOJQ2J1fEzt2OkCdDMBYaMeQYsPO0I3FRInrfikdNG4uMxP8QT9BjQRQmFaIYlNLk7lDXgdzYXNxb2cbCEw2KPXl7gx/2e299Lm/Ojh2SgIWwEVXqA27QoAEajabcbeLEiZU+R1xcHBqNhgMHDpTel5WVRbdu3WjatCkXL16sSkgWy8fJR+0QqkVrp8Up1ImChIIy9xdcLsC+jv3Nn6/XYu9lDwbI3JOJW+uKB3slr0jGNcoVpwZOKEaltKkaSqY0Xfu3NXsgM5Jp3xmx33usRs6XK/3AQtiMKtWAd+/ejeGa5rMjR47Qs2dP7r///moHkJycTJ8+fdBqtWzevBkfHx9Onz5d7fNZCh8nHy5lW+YeroZ8A4WJ/2wYUXilkLxzeehcdeh99Pj28eXCFxdIjUjFpYkL2YezyTqQRegLoaXPuTjrInZedtS9v2SkdG5sLkVpRTjVd6IorYikX5JQFAXfPr7lys+/lE/GrgwavtEQAId6DqCB1E2p2HvYU5BQgFOYFTfjA3aKlvdPtiR4+R4UY839msjZuQtFUdBoNDc/WAhh0apUA/b19aVu3bqlt19//ZXw8HC6du1arcIvXLhAly5d8PDwYMOGDfj4VFxrTElJYdiwYQQGBuLs7ExUVBTz588vc8zixYuJiorCyckJHx8fevToQU5ODlDSpN2uXTtcXFzw9PSkU6dOnDv3z36ry5cvp3Xr1jg6OhIWFsbrr79OcXFxta7pKl+n8onHUuSdzSP21VhiX40F4PL8y8S+GkvS0iSgpK82YFQAV1Zf4fTU06RtSqP+4/VxafxP/29hSiHF6f+8RkqRQtLSJGJejOH8jPPYe9kT9mIYOpey83oVRSH++3jqDquL1qHk7afVawkcF0jyimQufXeJeiPqldSirVRkUR3mrWpA8LJdUIPJF8CQkkLBqZgaPacQQh3V7gMuLCxk3rx5TJ48uVq/xk+ePMmzzz7L7bffzvz583FwuP480/z8fNq0acPzzz+Pu7s7q1atYsSIEYSHh9OuXTsSEhIYNmwYH3zwAYMGDSIrK4vNmzejKArFxcUMHDiQRx99lPnz51NYWMiuXbtKY968eTMjR47k008/pUuXLsTGxvLYY48B8Oqrr1bvxQHqONWp9nNNzbWJK82/b37DY7zu9MLrTq/rPh42JazM3y6RLjR6p9FNy9ZoNIS9FFbufveW7qWLcliz0WnN6Dv/LErGZZOVkbtjO44RjU12fiGEeWgURanW7swLFy7koYce4vz58wQEBFT6eXFxcYSGhqLX6+nUqRPr169HpytbS6rMIKx+/foRGRnJ9OnT2bdvH23atCEuLo6QkJAyx6WmpuLj48PGjRsrrKn36NGD7t27M2XKlNL75s2bx3PPPUd8fHylr+vfvj70NZ/u/7TazxfWxVGxY9rhKPxX7TZ5Wa533UXwlzNNXo4QwrSqvRDHt99+S58+faqUfK/Vv39/Nm/ezNKlS296rMFg4M033yQqKgpvb29cXV1Zu3Yt58+XLKN422230b17d6Kiorj//vv5+uuvSUsrmf7i7e3N6NGjiY6O5t577+WTTz4hISGh9NwHDx7kjTfewNXVtfT26KOPkpCQQG7u9Uf93kxdl7o3P0jYhJaFdZmzLMAsyRcgd8+eak9lEkJYjmol4HPnzvH7778zbty4ahf80ksv8corr/DQQw+xcOHCGx47bdo0PvnkE55//nn+/PNPDhw4QHR0NIWFJQOJdDod69evZ/Xq1TRt2pQZM2YQERHB2bNnAZg9ezbbt2+nY8eOLFiwgMaNG7Pj79Gk2dnZvP766xw4cKD0dvjwYWJiYnB0rP6CGvVcas/KTrXZhOQWvPRVGpqTZ8xWpjE7m/zDVV/IQwhhWarVBzx79mz8/Pzo27fvLRX+8ssvo9VqGT58OIqiMHTo0AqP27p1KwMGDODhhx8GwGg0curUKZo2bVp6jEajoVOnTnTq1IlXXnmFkJAQli1bxuTJkwFo1aoVrVq1YsqUKXTo0IGffvqJ9u3b07p1a06ePEnDhg1v6Vr+LcC1ei0Dwjq4GR2Yvj8Sr3V7r7uDkSnl7NiBU8uWKpQshKgpVU7ARqOR2bNnM2rUKOzsyj995MiRBAYG8u6771bqfC+99BI6nY7hw4djNBoZNmxYuWMaNWrE4sWL2bZtG15eXnz00UckJiaWJuCdO3fyxx9/0KtXL/z8/Ni5cyfJyck0adKEs2fPMmvWLPr3709AQAAnT54kJiaGkSNHAvDKK6/Qr18/6tevz3333YdWq+XgwYMcOXKEt956q6ovTyk/Zz90Gh0GRZoKbU2H/CCeXq7Amb2qxZCzYyd1/vMf1coXQty6Kifg33//nfPnz/PII49U+Pj58+fRaqvWsv3CCy+g1WoZMWIEiqKU61eeOnUqZ86cITo6GmdnZx577DEGDhxIRkYGAO7u7vz11198/PHHZGZmEhISwocffkifPn1ITEzkxIkTzJkzh5SUFOrVq8fEiRMZP348ANHR0fz666+88cYbvP/++9jb2xMZGXlLzesAdlo7gt2CicuMu6XzCMvy34SWtF9wBCVP3VXO8vbvx1hQgPYGsweEEJat2qOgxc1N3jiZ9efWqx2GqAE+Rmc+2BmO28Yb79trTvVnf4dLhw5qhyGEqCbZjtCEGnnefF6ssHx35zbgy5/cLCr5QkkztBDCekkCNqFGXpKArd3U8634zxfnUC5Y3rKiOTu2qx2CEOIWWORuSLaioWfNjqwW5lPX4Mr7W+rjtM08c3urI//IUQzZ2ehcXdUORQhRDVIDNqH67vVx1FV/LrFQxz054cz4QY/TtkNqh3JjBgO5uyz3B4IQ4sYkAZuQVqMlzLP8usfCMmkUeOtMa0Z/EYtyOUntcCpFmqGFsF6SgE1MmqGtQ0ixJ3P/iKDxgl1wizthmVPudtkfWAhrJX3AJtbYS3atsXT3ZUbw4ILLGK8cVTuUKis4fZrilBTsrrOVpxDCckkN2MQivCPUDkFch52iZdqp1jww8zjGKylqh1M9ikLODqkFC2GNJAGbWIs6LbDTSEODpWlU7MPc1aGELNkFRqPa4dySXEnAQlglScAm5mzvTFOfpjc/UJjNyLRmvPN1PrqDJ9UOpUbIghxCWCdJwGbQxr+N2iEIwEHR8enhVvT76hBKeoba4dSYogsXKLxoeQuFCCFuTBKwGdxe93a1Q6j1WhT688PyIOr+uhtscPnzXJmOJITVkQRsBq38WqHVyEutlvFXonh5Vgaa47Fqh2Iy0gwthPWR0UFm4KZ3I8IrguOpx9UOpVZxVfRM298Un7V7sL06b1k5Oy1zINahPy+SFJepdhjCRtw5rDF6R9tJW7ZzJRaujX8bScBm1K4gkGdWaOD0HrVDMQtD8hUKYmJwaGRZG4AUFxo4ufOy2mEIG9H5Act6f98qaRc1k9v9pR/YXJ66fBvPzkyC03Fqh2JWltgMHRTppXYIwoZotRq1Q6hRkoDNpI1/GzTY1pvH0ngZnfhmZws6zt6LkpendjhmZ4kLcvgGu+HgLA1tomZodLb1HSoJ2Ew8HT1p5tNM7TBsVte8EGbNd8d9wz61Q1FN7q5dKAaD2mGUodFqCGwstWBRM7QaScCimu6uf7faIdikKRda8vgXF1DO1+65sMasLPKPHVM7jHKkGVrUFFubTGJjl2PZutfvrnYINsXP6MKcv5rRat4elMJCtcOxCDkWuDuSJGBREzQa0OpsK2XZ1tVYuDDPMBq4N1A7DJvQOyecz+c64bT1oNqhWBRLXJDDq64LLh56tcMQVs7BxV7tEGqcJGAzk2boW6NR4I2zrXnki1iUeJne8m+5+/ZjtMDWgECpBYtb5ORmez/iJAGbmSTg6gsq9mDuhkgif94FxcVqh2ORlPx88vYfUDuMcoIivNUOQVg5J1epAYtb1KJOC/yc/NQOw+oMymrM/77XoN91RO1QLF6OBTZDSz+wuFVObpKAxS3SaDR0q99N7TCshg4NH5xqzbAvTqAkX1E7HKuQa4ELcrh5O+Lh66R2GMKKSRO0qBF3B0szdGU0KvJh7uqGNFiyC4xGtcOxGnmHD2PIzlE7jHKkFixuhTRBixrRtl5bvBzky+hGhqc34Z1vC7A7IOtnV1lxMbl7dqsdRTmBEfKeF9UnNWBRI+y19vQL76d2GBbJQdHx8dFWDPjyCEpautrhWC1LbIYOivRCVmMV1eUoNWBRU4Y0GqJ2CBaneZE/c1YEE7BiNyi2voGgaVniutBOrnp8Al3VDkNYKWepAYuaEu4Zzm2+t6kdhsUYl9KcV7/KRHvstNqh2ISCkycpTktTO4xygqQZWlSTo4yCFjVJasHgbLTniwMt6TXrAEpWltrh2A5FIXenhTZDC1ENTq5SAxY1KLpBNC72LmqHoZrbCwL4fmld6qzeo3YoNskS14UOaORpc3u6CtPTaDXSByxqlrO9M70b9FY7DFVMSryN57+8AjFn1Q7FZuVaYD+w3tEOvwZuaochrIyHr5NN/nCTBKyywY0Gqx2CWXkYHfl6Vws6f7cXJTdX7XBsWuG5cxQlJKgdRjlBkbIspaga73q22VIoCVhlLXxb0MirkdphmEXn/GC+WeCJxx/71A6l1rDEZmgZiCWqyques9ohmIQkYAtwf+P71Q7B5J6/1JInv4hHibuodii1Su5Oy0vAdcM8sLOXrx5Red4BUgMWJjKw4UCbXRnLz+DK7C3NafPDHpSCArXDqXUssQass9dSN9xD7TCEFfGuZ5vzxyUBWwAnOyeGNRmmdhg1rldOGJ/Pc8Rl8wG1Q6m1ipOSKDhzRu0wypHpSKKyNFoNXv7SBC1M6KHIh3C2s403mUaBV8+1ZtwXZ1DiL6sdTq1niatiyf7AorI8fJ3Q2WiXhW1elRXycPBgSGPrX5gj0ODODxub0OynXVBcrHY4Asi1wGZo3xA39E52aochrICtjoAGScAWZVTTUdhrrXeyef+sRnw8R4fDjsNqhyKukbtrF4qFbeeo1WoIbOypdhjCCtjqCGiQBGxR/F386RvWV+0wqkyHhndPt+bhmadQEpPVDkf8iyEjg/zjlreto2xPKCrDVkdAgyRgizOm+Rg0VrRnW1ixF3PXNCR80S4wGNQOR1yHJa6KJQOxRGXY6ghokARsccI8wugW3E3tMCrlwYxI3v+2GLv9lle7EmVZ4nQknwBXnN1tb4F9UXO0NjwCGiQBW6Txt4236FqwXtHx0bFWDJ55FCXV8ra8E+Xl7tuHUlSkdhjlSDO0uBG/Bm42OwIaJAFbpKY+Tbkn7B61w6hQ0yJffvg1hKDlu0FR1A5HVJKSm0vewYNqh1GONEOLGwlobNvvD0nAFmpSq0notZbVPDcmtRmvz8pBe+SU2qGIarDEZmhZF1rcSJAkYKGGANcAhjcZrnYYADgb7fnsUCv6fHUQJTNT7XBENeVY4LrQ7nWccK/jqHYYwgJpdRrqNrTtJUslAVuwcS3G4eGg7huwTWE9Zv9SD79Vu1WNQ9y6vIOHMFrgFpBSCxYV8W/gjr1ep3YYJiUJ2IK5690Z32K8auVPTGrBC1+mojlpeWsJi2ooKiJ37161oygnUPqBRQVqwwA9ScAW7sGIBwlyDTJrmR6KI7P23EbXb/eh5OSYtWxhWrIutLAWAbVgpTRJwBbOXmfPk22eNFt5HfOD+WaBN57rLa+mJG6dJa4L7eyut+nVjkTVae001Auz7f5fkARsFXo36E0L3xYmL+fZ+JY8PTMB5ex5k5cl1JF/4gSG9HS1wyhH+oHFtfwbuGNn4/2/IAnYaky9Yyp2GtPsHuNjdOa7bVG0nbMHJT/fJGUIC2E0krNrl9pRlCPzgcW1akP/L0gCthpNfJowotmIGj9v97wGfPmjK66b9tf4uYVlssR1oQMae6HRWu7qb8K8Am18/u9VkoCtyITbJlDfrX6Nne/l860Z//k5lIvxNXZOYfkscUEOByc7fOu7qR2GsAB2DjrqhrmrHYZZSAK2Io52jrzW8bVbXie6nsGNHzY2JerHXWCB6wPXlD25uUy4eIGup0/T9OQJfs/KKvN4jtHIW4mX6RZ7mlanTtLv7Bl+Tr/x2tZFisIXV64QfSaWlqdOMijuLJtzssscszIzg7tjT9M+5hTvJyWWeexSUSF9zsSSreLOUYVnz1KUmKRa+dcjzdACILRFHezsbb//FyQBW522ddsyqNGgaj+/X3ZDPp1jj+P2QzUYlWXKNRqJcHDkZX//Ch//ICmRzTk5vF+vHr+GhjLSy5u3ExPZkJ1V4fEAn15JZmFGOi/6+bOyQShDPTyZdOkSx/7uO08rLuaVy5d51tePr4OCWZmZycbsfxL0G4mJTPb1w1Wn7hdM7o7tqpZfEUnAAqBhGz+1QzAbScBW6L+3/5c6TnWq9BwdGt6Obc3ImadRLLD2Ywp3urrypK8vPdwqbtrcn5fHQHcP2jm7EGiv5wFPTyIcHDicd/2BaCsyMnnM24eurq4E6/U86OXFnS4ufJ+aCsCFoiJctVr6uLsT5eREO2dnYgsLAFiVmYmdRkPP68RjTpbYDF0v3AOdnXwl1WZ6JztCmvuoHYbZyLvdCrnr3ZnSbkqlj29Q7MkP6xrRaOEuKC42YWTWpZWTE3/mZJNYVISiKOzMzSGusIhOLtefk1qoGHHQlO0CcNBo2ZdXssRjiF5PvqJwLD+fdIOBI/n5RDg4kGEw8OmVZKb6VVwbN7ecnTvVDqEcO3sddcNrR9+fqFjYbXVq1Y+w2nOlNqZXg17cHXz3TY97IDOSad8Zsd97zAxRWZeX/PwJ1+vpdiaW206d5LGLF3nZ35/bna+/AXhnF1e+T0slrrAQo6KwLSeH37OzSP67T9dDp+PduvWYkpDA0HNx9Hd3p7OLK9OSkxju6cWloiIGx52l/9kzrM1Sb2OL4oQECuPiVCv/emRVrNqtYVvL+IFqLqaZWCrM4uUOL3Mg+QCp+anlHrNTtLx3siX1l+9BMRpViM7yzUtP42BePp8HBhJgZ8+evDzeTEzE186OjtepBU/x8+OVxMv0O3sGDRBsr2eQhwdLMzJKj+nh5lam2Xt3bi6nCgp4yc+f3mfOMD0ggDp2OoaeO8ftTs742KnzMczZsQN9gwaqlH09QZFe7FyhdhRCDY4u9gTXsnEAUgO2YnWc6vBmpzfL3R9RVIe5q0Kpv2wXSPKtUL7RyMfJyTzv50c3VzciHB0Z7uVFH3e30v7cinjb2fFZYBB7GzXm97BwVoWG4qzVEmRvX+HxhUYjbyRe5jX/upwvLMSAQltnZ0L1DjTQ6zmUn2eqS7ypnB2W1wztF+KGvWPtGAErygpr7YtWV7tSktSArdydQXcyvMlwfjz+IwCj0prRb/5ZlIzLKkdm2YoVhWIoN6FLiwYjyk2f76DV4q/VUqQorMvKordbxX2XX6am0NnFhaaOjhzLz6dY+efcRYqC4eZFmUzuzp0oioJGYzkLYGh1WgIbeRJ3OEXtUEqt3f8TB89uITH9PPY6B8LqNmXAHY/h7xlcekxRcSFLt89kb+yfFBuKaBLclqGdJ+HufP0m9czcVJbv/JrjF/eSV5hNw7otuL/z4/h5/LP5ypJtX7Dz1Dr0do4MuGMcbRv1KH1sX+wmdp1ax3/6vG2aCzezRrVo9PNVtevnho2a3GYyLTyaMuNQK/p+eRAlQ72+RUuSYzRyPD+f439PEbpUVMTx/Hzii4pw1elo6+TE9OQkduXmcLGwkGUZ6azIzKCH6z/Nxy8kxPNR8j+jxg/m5bE+K4sLhYXsyc3lsYsXUICx3uW/aE8XFLA6M5Mn6vgCEKbXo9VoWJKezqbsbM4WFhLlqN5m9Ia0NApOnFCt/OuxtGUIT8cf4s5m/Xlm4Gc83u8DDEYDn616joKif1ovlmz/giPndzC256s81f9/ZORc4Zt1r133nIqiMGvtK1zJTGB89Bu8MOQrvN38mPHrs6XnPRy3jT2nNzCx7/sMbP8YP236kOy8kq6OvIJsVu7+lgc6TzLptZuLs7u+1qx+dS1JwDZAr9PzzW3vUe/Po2qHYlGO5ucx5FwcQ87FAfB+chJDzsXx2ZVkAKYHBNLc0YnnEhK4N+4s36Sm8mQdX4Z6epaeI6GoiCvXjBwvVBQ+uZLMvXFnmRR/CX87O+bVr4/7v+b1KorCa4mXed7PH2dtycfMUavlnbr1+CLlClMvJzDVzx//6zRdm4slNkMHRVrWQKyJfd+jfURv6nk3IMgnnIfveo607CQuJMcAJclw+4nVDO7wHyICW1HftzEP3/UcZxKPcjax4sGPSRkXiUs6zoNdniLELxJ/z2CGdnmKouJC9p7eAMDl9PM0CriNEN8Ibm94N456Z1KyEgD4ZecsujTtj7ebbQxaCm/tVyuXIpUmaBvhFBpK3TfeIP6ZZ9QOxWK0c3bhWETkdR/3tbPjnXr1bniOOfVDyvzd1tmZX0PDblq2RqNh3r+eC3CXqyt3uTa86fPNJWfHdnzGjFY7jDJ8Al1wcrMnL8syV2nLLyzZI9vZsaSl5PyVGAzGYiIC25QeU9erPl6ufpxNPEaof9Ny5yg2lFybnU5fep9Wo8VOZ0/s5SN0bNKXQJ9wth5fRW5BFlcyEygqLsTXI5DYhMNcuHKaoZ3Nt02pqTW6vfY1P4PUgG2KR7++eD44VO0whBXJ270HxcLmhms0GottjjQqRhZv+5ywus0J8A4FSvpy7bT2ODu4ljnW3cmLzNyKB/TV9SxJ0Ct2fUNuQRbFhiLWH5hPek4yGX8/p2lwW9o26sEHSycwd+MHjOj2PHo7R37e8gkPdnmKzcdW8sbPo/jol0kkpMaZ9LpNyTvAhXoNPdUOQxWSgG2M/4sv4ti0/C9uISpizM0l79BhtcMox1KXpVy45VMSUuMY033qLZ1Hp7Pj0V6vk5Rxkee+H8jkb+/h1KWDNA1uh/aaQXF9bx/Fa8Pm8tL933BbaGfW7Z9PZGBrdFoda/bN4+kBn9Ah8h5++PO9W7001bToFnTzg2yUJGAbo9XrCfzkY3TX9GMKcSM5si50pSzc8ilHzu1g0r0f4uXqW3q/u7M3xcYicgvKbsqRmZd2w1HQ9X0bM+W+WUwbvZy3RyxiYt/3yCnIxMet4m6Ry2nn2R3zO/3ajiEm/iAN67XAzcmT1uFduXAlhvzC3Jq5UDNydLEn4o66aoehGknANkgfHEzQZzPQ6PU3P1jUerkWuC60h68zbt7qjRC/lqIoLNzyKQfPbmHSvdOp4142Qdav0wid1o6Tl/aV3peYfoG07KQK+3//zcnBFTcnT5IyLnI++RQtGnSqMIafN/+PwR3+g4O9E0bFiMFY0nVgMJaswmZUrG/Of9MuAdjpa++8b0nANsr59tup9/bbYEFzPIVlyjt4EGP+9TegUEughdSCF275lN0xvzO6+0s42juTmZtKZm4qhcUlm2w4ObjSIbIPS7fP5NSl/ZxPPsW8jR8Q6t+0TAJ+c8FoDp7dUvr3vthNnIo/wJXMeA7FbeWzX5+jRYNONAm+vVwM2078hqujB1ENOgIQVrc5p+IPcDbxGH8eWkxdr5ByfdCWTqvVENW19jY/g4yCtmke9/aj6OIFkj/5VO1QhAVTCgvJ3bsX107la15qCorw4sS2BLXDYPOxkrUxP1k5ucz9D9/1LO0jegMwpMMENGj4Zv3rJQtxBN3O0C5lRyknpl8gr/CfZurM3BSWbp9J1t9N1Xc07kXv1g+XKz8zN5W1+35k8sB/PscN/CLp3uI+Zq5+ETcnL0Z0e77Grtdcwlv74urloHYYqtIoiqLiWjzCHOKnvEjGsmVqhyEsmM+j4/D773/VDqOMnIwCvn9+q9phCBMZ8nwb6oZ6qB2GqqQJuhao98brOLdvr3YYwoJZ4oIcLh4OeNW9/s5Uwnr5h7rX+uQLkoBrBY29PUGffoI+PFztUISFyj96FEOm5S1hammrYomacdvdwTc/qBaQBFxL6NzdCf7qK3R16qgdirBERiO5u3apHUU5QRa2LrS4da5eDoS39r35gbWAJOBaRB8USPAXn6NxclI7FGGBLLEZOqCxpwzktzHNuwbWum0Hr0dehVrGqUULgmd+gUbFXXiEZbLEBTkcXezxre928wOFVXB0sa/1U4+uJQm4FnJp357gL2dKEhZlFJ6OpTg5We0wyrG07QlF9bXpE4LeSWa/XiUJuJaSJCwqYonN0Ja4LKWoOjdvR6n9/osk4FpMkrD4N0tshq7X0BOtnXQEW7t2/UPR2UvKuZa8GrWcJGFxrVwLrAHb63UyZ9TK+QS6ENGu9m66cD2SgIUkYVGq6NIlCi9cUDuMcqQZ2rq1HxiORiutGP8mCVgAkoTFP3K2W14ztMwHtl4BjTxpECXrD1REErAodTUJa11c1A5FqMgSm6H9Qt2xd6i929ZZsw6DZAW+65EELMpwad+ekB/nYVdX+mtqq5ydO7G0PVp0Oi31GnqqHYaoorCWvtQNk/7765EELMpxjIykwYKfcWjSRO1QhAoMKSkUnIpRO4xypB/Yumi0GtoPDFM7DIsmCVhUyN7fnwbz5uLatavaoQgV5O7coXYI5Ug/sHVp0qkeXnWlO+tGJAGL69K6uBD0xed4DR+udijCzHK2W14CrhPsiqOLvdphiEpwctfTYaD0/d6MJGBxQxqdjrovT8V/yguglbdLbZG7ezeKwaB2GGVoNBoCIzzVDkNUwp1DG8uPpUqQb1RRKd6jRhE041PZSamWMGZnk3/kiNphlCPN0JYvrJUvDdv4qR2GVZAELCrNrXt3Qn74ATs/+XDVBpbYDB0U6a12COIGHJztuPPBxmqHYTUkAYsqcYpqTugvy3Dp3FntUISJ5eywvATs6e+Mq5eD2mGI6+g4pCEuHvLvU1mSgEWV2Xl7E/z1LPye+S/YydZitipv/36MBQVqh1GObE9omYIivWjaKUDtMKyKJGBRLRqNBp9x4wiZ+wP2AfKhs0VKQQF5+/erHUY5Mh/Y8tg56Oj2cKTaYVgdScDilji3akXosqW49eyhdijCBCyyHzhC+oEtTfv+YbjXkQGaVSUJWNwynYcHQTNm4D91Khq9Xu1wRA3KtcB+YFcvBzz9ndUOQ/zNP9SdFt2C1A7DKkkCFjXG++HhNFjwM/qQELVDETUk78gRDNnZaodRjkxHsgxaOw13j2giWw1WkyRgUaMcmzQhdOkSvB4aJgt32AKDgdxdu9WOohzpB7YMHQc3xDtAlpusLvmGFDVO6+JC3VdeIeTHeTg0aqR2OOIWWeK60IERXiCVLlWFtfLltruD1Q7DqkkCFibj3KoVoUuX4PvUU2gcZG6gtbLEgViOLvbUCXJVO4xay72OI3ePlN3SbpUkYGFSGnt76vxnPGErluPcob3a4YhqKIiJoTglRe0wypFVsdShtdMQ/WhzHJxkDYBbJQlYmIU+JISQ2bOp99676Lyk/86qKAq5O3eqHUU5MhBLHZ2GNMIvxF3tMGyCJGBhVp4DBxL22yo8BgxQOxRRBZbYDB3QyBOtTjqCzanxHf4y5agGSQIWZmfn5UXA++8R8uM8nFq3VjscUQmWuC60vYMO/1CpiZlLnWBXug2X1a5qkiRgoRrnNm1o8NOPBH3xBQ6NZQcVS1Z04QJFly6pHUY5si60eTi62NNnfBR2ep3aodgUScBCdW53dyP0l2UEvP8e9oGBaocjrsMSa8HBMh/Y5DRaDb3GNbOKpSbj4uLQaDQcOHBA7VAqRRKwsAgarRaPAQMIX/0b/i+9hM7HR+2QxL9YYj+wf6gHdnr5GjOlDoPCCW5yayPOs7KyeOqppwgJCcHJyYmOHTuye3fVF3jRaDT88ssvpX8XFRUxbNgwAgMDOXLkyC3FqAZ55wqLotHr8R7xMA3XraXOE4+jdZW5npbCEkdC6+y01GvoqXYYNuu2HsG06ln/ls8zbtw41q9fz9y5czl8+DC9evWiR48eXLqFbo3c3Fz69+/P7t272bJlC82bN7/lOM1NErCwSFoXF3wnTiR8/TrqTJwoNWILUJycTMHp02qHUY5MRzKNiDvq0mlIw1s+T15eHkuWLOGDDz7gzjvvpGHDhrz22ms0bNiQmTNnVuuc6enp9OzZk/j4eLZs2UJoaGiFxxkMBsaOHUtoaChOTk5ERETwySeflDlm48aNtGvXDhcXFzw9PenUqRPnzp0D4ODBg3Tr1g03Nzfc3d1p06YNe/bsKX3uli1b6NKlC05OTgQHBzNp0iRycnIqfR2SgIVFs/PywveJx2n45wbqvf02DhERaodUq1liM7SsC13zQqJ8uHtkJBrNrU/zKi4uxmAw4OjoWOZ+JycntmzZUuXzXb58ma5duwKwadMm6tate91jjUYjQUFBLFq0iGPHjvHKK6/w4osvsnDhwtLYBg4cSNeuXTl06BDbt2/nscceK73u4cOHExQUxO7du9m7dy8vvPAC9vb2AMTGxtK7d2+GDBnCoUOHWLBgAVu2bOHxxx+v9LVoFEVRqvwKCKGinB07SP1+DtmbNoG8fc3KtUd3gj/7TO0wylCMCt8+s5mC3GK1Q7EJ9cI96P9kyxod8dyxY0f0ej0//fQT/v7+zJ8/n1GjRtGwYUNOnjxZ6fNoNBr0ej1hYWHs3bsXZ+ey21LGxcURGhrK/v37admyZYXnePzxx7l8+TKLFy8mNTUVHx8fNm7cWJrUr+Xu7s6MGTMYNWpUucfGjRuHTqfjq6++Kr1vy5YtdO3alZycnHI/OCoiNWBhdVzatyf4y5mEr/4Nr4ceQuMse8OaS+6u3SgGg9phlKHRaghsLLXgmuAd4MI9E1rU+HSjuXPnoigKgYGBODg48OmnnzJs2DC01dgxrV+/fpw6dapM4ruRzz//nDZt2uDr64urqyuzZs3i/PnzAHh7ezN69Giio6O59957+eSTT0hISCh97uTJkxk3bhw9evTgvffeIzY2tvSxgwcP8v333+Pq6lp6i46Oxmg0cvbs2UrFJglYWC19gwbUfeVlGm38E79nn8G+/q0PFhE3ZszMJP/YMbXDKEfmA986N29H+k9qiaOLfY2fOzw8nE2bNpGdnc2FCxfYtWsXRUVFhIWFVflcI0aM4LvvvuOZZ57ho48+uuGxP//8M8888wxjx45l3bp1HDhwgDFjxlBYWFh6zOzZs9m+fTsdO3ZkwYIFNG7cmB1/T7l77bXXOHr0KH379mXDhg00bdqUZcuWAZCdnc348eM5cOBA6e3gwYPExMQQHh5eqWuR1bSF1dO5u+Mzdiw+Y8eSu28fGb8sJ3PNGoyZmWqHZpNyduzAKSpK7TDKkH7gW+PkZk//J1vi4mnaXctcXFxwcXEhLS2NtWvX8sEHH1TrPKNGjUKr1TJmzBiMRiPPPPNMhcdt3bqVjh07MmHChNL7rq3FXtWqVStatWrFlClT6NChAz/99BPt25dsHtO4cWMaN27M008/zbBhw5g9ezaDBg2idevWHDt2jIYNqz9QTWrAwqY4t25NvTdep9GWzQR+/D9cu3dHo9erHZZNybXAgVje9Vxw8ZB/5+qwd9TR7/Hb8PQ3XVfO2rVrWbNmDWfPnmX9+vV069aNyMhIxowZU3rMlClTGDlyZKXPOWLECObMmcMLL7zAtGnTKjymUaNG7Nmzh7Vr13Lq1ClefvnlMvOPz549y5QpU9i+fTvnzp1j3bp1xMTE0KRJE/Ly8nj88cfZuHEj586dY+vWrezevZsmTUq2YXz++efZtm0bjz/+OAcOHCAmJobly5dXaRCW1ICFTdLq9bj37o17794YsrLI+uMPMlevJmfbdigqUjs8q5a7bx9KYaHF/bAJjPDi1K5EtcOwKnb2Wvr8J8rkuxtlZGQwZcoULl68iLe3N0OGDOHtt98uHVEMkJCQUNo3W1nDhw9Hq9UyYsQIjEYjQ4cOLfP4+PHj2b9/P0OHDkWj0TBs2DAmTJjA6tWrAXB2dubEiRPMmTOHlJQU6tWrx8SJExk/fjzFxcWkpKQwcuRIEhMTqVOnDoMHD+b1118HoEWLFmzatImXXnqJLl26oCgK4eHh5WK4ERkFLWoVQ3o6WX9sIGfrFnK278CQlqZ2SFap/g9zcGnXTu0wyji+LZ4NP5xQOwyr4eBsR98JLWQhExVJDVjUKjpPTzyHDMZzyGAURSH/6DFytm0jZ+tW8vbtQ5HacaXk7thhcQk4KPLWlkusTZzc9fSfdBt1gtzUDqVWkxqwEH8z5uWRu3s3OVu3kbNtKwUxlrfqk6o0GhwiInBu2xb3Xj1xbttW7YjKmfvydjKT89QOw6K5+TjS/8mWePrJ9D21SQIW4jqKEpPI27eX/GPHyT9+nPxjxzCkpqodltnoPDxwiIjAsVkznNvejnObNug8PNQO64b+/PEExzbHqx2GxfIOcKH/JNOPdhaVIwlYiCooSkwk/9ixktvfSbk4PuHmT7RkOh36Bg1wjGiMQ0QkjpEROEREYH+DJf4sVcyeRNZ9c1TtMCySf6g7/R6/zSTzfEX1SAIW4hYZ0tPJP36cwnPnKIpPoCghgaKEeIrjEyhKSoJiC1gi0c4OO19f7P38sPP3x75ePRwaN8IhIhKHRg3ROthGjSgvq5DvntsC8q1WRlCkF33+E4XeUYb9WBJJwOKWVGbt1dpMMRopTkr6OzHHU5yQQFHCZQxZmSh5+Rjz8v6+5aLk5l3zd1756VJ2dmj1ejQODmgcHf/5fwcHNA56tA6O2NWpg13dutj5+2Hv74+dnz92/n7Y1amDphrL/lmjn9/cRcqlbLXDsBjhrXzpObYZOrva8e9vTeTnkI0yGAy89tprzJs3j8uXLxMQEMDo0aOZOnVqlXY40Wg0LFu2jIEDBwIlG2CPHDmSv/76i7Vr1+Iq+/XekEarxb5u3b+bc1tV6blKURHGggI0Wm1JktXV7Pq8tioo0ksS8N+adKrHXcMj0WpvfVcjUfMkAduo999/n5kzZzJnzhyaNWvGnj17GDNmDB4eHkyaNKla58zNzWXIkCHExMSU7sEZFxdXs4GLUhp7e3T20l9XVUERXhz844LaYahKq9XQcUhDbuserHYo4gakTcJGbdu2jQEDBtC3b18aNGjAfffdR69evdi1a1e1zmcrG2AL2xfQ2LNW1/ic3fUMeLqVJF8rIAnYRnXs2JE//viDU6dOASWJbcuWLfTp06fK57KlDbCF7dM72uHXoHYuMFEv3IMHXmpLQCNPtUMRlSCDsGyU0WjkxRdf5IMPPkCn02EwGHj77beZMmVKlc5jaxtgi9phx/JY9q4+p3YYZhXVLYhO9zVEp5N6lbWQfykbtXDhQn788Ud++ukn9u3bx5w5c5g+fTpz5syp8rlsaQNsUTvUpmUp7fRaeoxpyp1DG0vytTJSA7ZRwcHBvPDCC0ycOLH0vrfeeot58+Zx4kTlF6y/Ogo6IyODRx55hGnTpjF58uTSx/9dA/75558ZM2YMH374IR06dMDNzY1p06axc+dODhw4UPq8/fv3s2bNGlauXMnhw4dZv3596f6bp06dYtWqVaxevZpNmzbx888/M2jQIJo0aULPnj0rHERWv3599Ba2O49Qj6HIyDeT/6K4yKh2KCbl7utEn/FR1AmS2QjWSEZB26jc3Fy0/5r3qdPpMBqr94VkKxtgi9pBZ6+lbrgHF0/Y7m5XIVE+9BzTFAdnGSlvraS9wkbde++9vP3226xatYq4uDiWLVvGRx99xKBBg0qPqY0bYIvaIyjSS+0QTEJnp6XDoHD6TmghydfKSQ3YRs2YMYOXX36ZCRMmkJSUREBAAOPHj+eVV14pPaY2boAtao+gCG/gjNph1Cj/UHfuHtkE73ouaociaoD0AQshbJLRqPDtfzdTmGcBa3HfIjt7Le36h9GyezCaWjzH2dZIDVgIYZO0Wg0BjTyJO3RF7VBuSb2GHtw9ogme/rJ/r62RBCyEsFlBkV5Wm4Dt9FraDwinRbcgqfXaKEnAQgibFRRhnQOxAhp5cvfISDx8pdZryyQBCyFslk+gK07uevIyC9UOpVLsHXR0GBRO866BVdq1TFgnScBCCJsWFOFFzO5EtcO4IY1WQ2SHutxxbxgung5qhyPMRBKwEMKmWXoCDmnuQ4dB4fgEympWtY0kYCGETbPUBTl867vRcUhDq+2nFrdOErAQwqa513HCvY4jmVfy1Q4FADcfR9oPCKNRW3/p563lJAELIWxeYIQXmVcSbn6gCTk429GmTwNa3BWEzl5WARaSgIUQtUBQpBfHt6qTgO3stTTvGkibPg1wdJG1m8U/JAELIWxeybrQ5uXkrieqayDNuwbi5CpbZYryJAELIWyes7se7wAXUuNzTF6Wd4ALt3UPJqJdXWlqFjckCVgIUSsERXiZNAEHN/WmZY9g6jf1MVkZwrZIAhZC1ApBkV4c+vNijZ5TZ6elcTt/buseLPN4RZVJAhZC1AoBjb3QaDUoxlvfgdXZXU/TzgFE3RWEs7v074rqkQQshKgVHJzs8K3vRlJcZrWer3eyI7yVL43a+hMU4SU7FIlbJglYCFFrBEV6VSkB6+y1NIjyoXHbuoQ095FBVaJGSQIWQtQaQRFe7Ftz7obHaLQagiO9aNTOn7CWvugd5WtSmIa8s4QQtUa9cA90dloMxcYy92u0GuqGutPwdn8atvGTfl1hFpKAhRC1hp1eR91wdy6dTMfV24H6TbwJbupDUKSXrFIlzE6jKMqtDwkUQggrkXQuE3sHHV51XdQORdRykoCFEEIIFciQPiGEEEIFkoCFEEIIFUgCFkIIIVQgCVgIIYRQgSRgIYQQQgWSgIUQQggVSAIWQgghVCAJWAghhFCBJGAhhBBCBZKAhRBCCBVIAhZCCCFUIAlYCCGEUIEkYCGEEEIFkoCFEEIIFfw/C+uTdmTPiTEAAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"# BEGIN SOLUTION\n",
|
||
"plt.pie(\n",
|
||
" sec_school.values(),\n",
|
||
" labels=sec_school.keys(),\n",
|
||
" autopct='%1.1f%%',\n",
|
||
" explode=[0, 0.25, 0, 0, 0.4]\n",
|
||
")\n",
|
||
"\n",
|
||
"plt.title(\"Klassenverteilung einer Grundschule\")\n",
|
||
"\n",
|
||
"plt.show()\n",
|
||
"# END SOLUTION"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "71899ae9-85bb-49ef-a077-1d5caaa4913f",
|
||
"metadata": {},
|
||
"source": [
|
||
"# Bonus\n",
|
||
"\n",
|
||
"Programmatisch lässt sich das Meme, wie folgt, generieren:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 79,
|
||
"id": "c3883c67-06ab-4713-ad96-5706522a7bc3",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"data": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAAArUAAAF2CAYAAABwNGDGAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjcsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvTLEjVAAAAAlwSFlzAAAPYQAAD2EBqD+naQAAVzpJREFUeJzt3Xd4U2X/P/D3SdKmI+luoZNSoGVvECy70FbLHrJtFX0QWc8jPA4UhJ+4UHEBIipKAUWWWLbShwLKEEFAQIbsUVoobaErbcbvj9p8KU2hI8nJSd6v6+JCk5NzPglp+s59Pue+BYPBYAARERERkYTJxC6AiIiIiKi2GGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIYaomIiIhI8hhqiYiIiEjyGGqJiIiISPIUYhdAVF0lOgNyi/XIKdYhR6Mv/W9N6X/nFOv++f/S24t1BggCIOCfPwIgEwQ4ywAXhQwucgEucgFKuQAvpQx13RQIdFOgrpscgW4KuDnxex8REZEUMNSSTcoo0OLv3BL8nVv8z9+l/33uTgmyNXqr1eHhLDMGXGPYdVegvtoJzX2cEenlDLlMsFo9REREZJpgMBgMYhdBjutcbjH2ZxTheJYGf98pDa/ncktwt8R6wbU2XOQCmng7o4WvEi18/vnbV4kgd35fJCIisiaGWrKa/BI9DmYWYd+NIuzPKMT+jCJkFurELssifF1kaOFTGnA7BrigV4gbgy4REZEFMdSSxfydW4x9N4qw70ZpgD2WpYHOgd9tUV5O6BXshl4hbugZ7AZfF7nYJREREdkNhloym/wSPVKvFmDLpXxsuZyPK3lasUuyWQKAVn7K0pAb7IpuQW5QO/OiNCIioppiqKVauZpXgg0X8rDpYj7SrhdC48hDsbWgkAEdA1zQL1yFYQ1UaODpLHZJREREksJQS9V2JqcY68/nYf35u/g9UwO+gcyvtZ8SQyNUGNZQjUgvBlwiIqKHYailKrlVqMOy07n45tQdHL9dLHY5DqWNnxKjI9UY1cgDgbzYjIiIyCSGWqqUwWBA6tUCfHEyFxsu5KNYz7eKmGQC0DPYDWMi1RgSoWYPLhER0T0YaqmC9Hwtvj6Vi6/+uoPzd0rELodMUDvJkNTYA1NaeqEh+2+JiIgYaqmUTm/Atsv5+OKvXGy+lA+tNNY+cHgyAXg8zB1TW3qhd6i72OUQERGJhqHWweWV6LHoeA4+PZaDq/mcgkvKmvs4Y0pLL4yJ9ICrgq0JRETkWBhqHVSuRodP/8zBR8eykVXEYVl74usiw7+aemFic08Eq5zELoeIiMgqGGodzO0iHT48mo1P/8xBbjHDrD1TyIAnGqjxegdfTgtGRER2j6HWQWQWaPHB0WwsOp6DvBL+kzsShQx4qrEnZnfwRRCnBCMiIjvFUGvnrudr8d4ft7HkZC4KtPyndmSuCgGTmnvhlbY+8HaRi10OERGRWTHU2qm8Ej3e+D0LHx/L4dK1VI6XUob/tvbGv1t6w82JF5QREZF9YKi1QytO38GL+24ivUAndilkwwLd5JjZ3hfPNvWEQiaIXQ4REVGtMNTakT9uFmHynkz8eqNI7FJIQhp6OuHtTn4Y2kAtdilEREQ1xlBrB7KKdHjtwC0sOZkLrmRLNdW3njsWdQtAqJrTgBERkfQw1EqYTm/A5ydzMfPALdzWcHouqj21kwxvdfLF8829IBPYkkBERNLBUCtRv6YXYtKeTBy5pRG7FLJDneq44IseddDcVyl2KURERFXCUCsxhVo9Xt53C5/+mQP+w5ElOcmAl9r44LX2PlDKOUsCERHZNoZaCTmQUYjE1Bs4nVMidinkQKK8nLCkRx10C3ITuxQiIqJKMdRKQLHOgNkHszDvj9vglLMkBgHAs009MT/aH+6c25aIiGwQQ62NO51djJE/p+MP9s6SDYj0csL3sYFo7ecidilERETlMNTasC9P5uLfv2Qin8vbkg1RygXM6+yHKS29xS6FiIjIiKHWBmUX6fCvXRlYey5P7FKIKtU/3B1f96oLHxe52KUQEREx1NqaP24WYeDW67icpxW7FKKHqqdWYG1cENoHsB2BiIjExVBrQ9aeu4vE1BsoYLsBSYhSLuDjLv4Y38xL7FKIiMiBMdTaAIOhdHaDN36/zblnSbISozzwWfcAuCo4OwIREVkfQ63ICkr0eDL1BtadZ/8sSV9rPyU2PR6EYJWT2KUQEZGDYagV0eW7JRiw9TqXuiW7EqpSYGvfYDTz4RK7RERkPQy1ItmbXohB264js1AndilEZuellGFDfBC6B3MVMiIisg6GWhF8/VcuntuViWI9X3qyX0q5gGW96mJ4I7XYpRARkQPgFR1W9ur+W3h6ZwYDLdk9jc6AkT+n44Mjt8UuhYiIHABHaq3o379k4uNjOWKXQWR1U1t6YX60P2SCIHYpRERkpxhqrcBgMOD53ZlYfCJX7FKIRDO0gQrLY+rChVN+ERGRBTDUWpjeYMC4nRn45tQdsUshEl2XQFdsejwInkourUtERObFUGtBWr0BY3fcwKq/74pdCpHNeLSuC7b3C4HKiSO2RERkPvytYiHFOgOe2J7OQEt0n703itB38zUUavVil0JERHaEodYCirR6DNp6HT9c4CphRKbsul6IgVuvQ6NjsCUiIvNgqDWzghI9+m65ji2X88Uuhcim/XSlAMO2p6NExw4oIiKqPYZaM9LqDRiy/TpSrxaIXQqRJGy8mI9RO9Kh47zNRERUSwy1ZvRsWga2XWagJaqOtefykJh6A3pes0pERLXAUGsms367xWm7iGpo5dm7+FdaBjgZCxER1RRDrRl8eTIXb/zOpUCJauOrv+5g6i83xS6DiIgkiqG2lrZcysOE3Rlil0FkFz79MwcL/swWuwwiIpIgLr5QC79nFqHHhivI1/IlJDIXhQzY1jcEMSFuYpdCREQSwpHaGjqfW4yEzdcYaInMTKsHhm2/jr9zi8UuhYiIJIShtgZuFeoQv+kaMgt1YpdCZJeyNXr023wduRr+jBERUdUw1FZTic6AgVuv4WxuidilENm1UznFGPlzOqf6IiKiKmGoraZpe2/i1xtFYpdB5BC2Xi7Ai3tviV0GERFJAENtNaw6ewef/pkjdhlEDuWDo9lYdipX7DKIiMjGcfaDKjp5W4OOay/zwjAiESjlAnYOCEHnuq5il0JERDaKI7VVkFeix5Bt6Qy0RCLR6AwYvO06Mgu0YpdCREQ2iqG2CibsysCpHE4vRCSmGwU6PPU/LnRCRESmMdQ+RPKpO1hx5q7YZRARgC2X8/HJMa44RkREFbGn9gHO5BSj3ZpLyCvhS0RkK5RyAb8NCUNLP6XYpRARkQ3hSG0lNDo9RvyUzkBLZGM0OgNG/pyOQq1e7FKIiMiGMNRWYuaBLPxxSyN2GURkwsnsYszYz/lriYjo/7D9wITDN4vQce1l6PjKENksAcDOASHoHuwmdilERGQDOFJ7H53egGfTMhhoiWycAUDS/24gr4RtCERExFBbwYdHs3H4JtsOiKTg4l0tXvj1pthlEBGRDWD7wT0u3ClB81UXUcBFFogk5ed+wegd6i52GUREJCKO1N5jfFoGAy2RBE355SZK2DNEROTQGGr/sfz0Hfx8tUDsMoioBv7KLsanf+aIXQYREYmI7QcAbhXq0OS7i7hVpBO7FCKqIQ9nGc6MCkcdN4XYpRARkQg4UgvgP79mMtASSdydYj1e5ty1REQOy+FD7Y4r+Vhx5q7YZRCRGSw7dQf7bxSKXQYREYnAoUOtwWDA9L0c2SGyFwYAk/dkQs+uKiIih+PQofa7s3dxNItz0hLZk99varD0rztil0FERFbmsKG2RGfArN+yxC6DiCxgxoFbyNGwT56IyJE4bKj94q9cnLtTInYZRGQBNwt1eJ1fWomIHIpDhtqCEj3e+J2/8Ijs2WcncnDpLr+4EhE5CocMtR8dy8aNAp6aJLJnJXrg3cO3xS6DiIisxOFC7e0iHeb9kS12GURkBUtP3cH1fK3YZRARkRU4XKh9+/Bt5BbrxS6DiKxAozNg3h8crSUicgQOFWqv5ZVgAdeHJ3IoS07mIrOAo7VERPbOoULtm4duo0jHSdmJHEmh1oAPjrLliIjI3jlMqL1dpMM3pzkhO5EjWnQ8B1lFvDiUiMieOUyoXXIyF4VajtISOaK8EgM+4mgtEZFdc4hQq9UbsJC9tEQO7dM/c5DLVcaIiOyWQ4Ta9efzcJXT+hA5tNxiPT7hl1siIrvlEKH242M87UhEpb21Wj3bkIiI7JHdh9qDGUXYe6NI7DKIyAbcKNBh08V8scsgIiILsPtQy1FaIrrXFydzxS6BiIgswK5DbXq+FqvP3RW7DCKyIduu5OPK3RKxyyAiIjOz61C76HgOSrgiLhHdQ28Alp7inNVERPbGbkNtsc6Az3makYhMWPpXLvQGXjBGRGRP7DbUbr6Uh5uFnJOSiCq6nKfF9ssFYpdBRERmZLehdsUZ9tISUeV4wRgRkX2xy1Cbo9Fh8yVO20NEldt4KQ83CrgoCxGRvbDLULv2XB40OvbLEVHltHrgG14wRkRkN+wy1K48w19URPRwyxhqiYjsht2F2vR8LXanF4pdBhFJwKmcYpy8rRG7DCIiMgO7C7Xrzt8Fl3Ynoqpafz5P7BKIiMgM7C7Urj3HX1BEVHUMtURE9kEhdgHmlFmgxR62HhBRNfxxS4OLd0oQ7uEkdilWJyw6Y5H9Gp6PtMh+iYgexK5Gatefz2PrARFV24YLHK2VgrNnz2LSpElo2rQp3N3d4eLigpCQEHTo0AGTJk3CunXrym0fHh4OQRBw8eJFcQomIquyq5HalIv8xURE1bfpUj7+3cpb7DLoAdavX49Ro0ZBo9HA19cX0dHR8Pf3R3Z2No4cOYKFCxdi1apVGDJkiNilEpFI7CbUlugMbD0gohrZc70Qd4v1UDvb1ckru5GRkYHExERoNBpMmzYNc+fOhYuLS7ltDh06hLVr14pUIRHZArsJtb9lFiGvhL0HRFR9xXoDdlzNx6AItdilkAmbNm1CXl4egoKC8P7775vcpl27dmjXrp2VKyMiW2I3wxL/u1YgdglEJGFcWtt2ZWRkAAD8/f3Nts+5c+dCEASEhobi6NGjiIiIgCAI2LdvX6WPef755yEIAl588UWz1UFE5mM/ofYqQy0R1dyWS/kwGHi2xxaFhYUBAI4fP47U1NRa7aukpARPP/00Zs6cidatW+PAgQNo1aoVJk2aBABYsGCBycfduXMHy5cvh0wmw/PPP1+rGojIMuwi1BZq9diXUSR2GUQkYekFOpzJKRG7DDJh4MCBCA4Ohk6nQ58+fdCzZ0/MnTsXW7Zswc2bN6u8n9zcXDz++OP4+uuv8dhjj2HPnj0ICgoCAIwbNw7u7u5Yu3atcWT4XsnJycjLy0NCQgLCw8PN9dSIyIzsItT+ml4IjY4jLERUO/szeLGpLVKpVEhNTcUjjzwCg8GAtLQ0zJw5EwkJCQgICECbNm2wePFi6HS6Svdx+fJldOnSBTt27MD48eOxceNGqFQq4/2enp5ITExEcXExvvjiiwqPX7hwIQAYR3SJyPbYRaj93zX+IiKi2tt3g2d8bFVUVBT279+PAwcOYNasWYiLizP22B45cgQTJkxAfHw8iouLKzz28OHD6NSpE06cOIF33nkHixcvhlwur7DdlClTIAgCPv/8c2i1WuPtqampOHXqFKKiotCnTx/LPUkiqhU7CbXspyWi2tvHkVqb17FjR8yZMwfbtm1DRkYGDh06hBEjRgAAduzYgY8//rjCY4YPH4709HS88cYbeOmllyrdd1RUFGJjY3H16lVs2LDBeHvZKG3ZhWJEZJskH2rvFOvweyZHV4io9o7fLkZeiV7sMqiKBEFA27Zt8d1336F///4AUC6MlklMTAQAfPjhhzh06NAD9zl16lQA/xdkr1y5gpSUFKhUKiQlJZmveCIyO8mH2t3XC8F2WiIyB70B+I0XnUpSbGwsAODWrVsV7nvttdfwwQcfICsrC7169cIvv/xS6X7i4+MRGRmJtLQ0nDhxwtirO3bsWHh4eFisfiKqPcmH2t84SktEZrTvBlsQbE1Vplq7fPkyACAkJMTk/S+88AKWLFmCvLw8xMXF4eeffza5nSAImDx5MgBg/vz5+PLLLwHwAjEiKZB8qD2WpRG7BCKyI5we0PYsWrQIiYmJ2Lt3b4X7DAYD1q9fb5xftqy/1pRnn30WK1asQHFxMfr162eyVQEAkpKS4OnpiaVLlyIzMxM9e/ZE06ZNzfJciMhyJB9q/8yqeKUrEVFNcVov21NSUoLk5GRER0cjICAAcXFxGD16NBISEhAREYEhQ4agoKAAY8aMwbhx4x64r5EjR2LdunUAgGHDhmHlypUVtlGpVHjqqaeM/89RWiJpkHSozSvR48IdTpZOROaTVaTH2Rx+WbYl48aNw4YNGzB58mTUr18fJ0+exJo1a7Bz507I5XKMHDkSW7duNa749TD9+/fH5s2boVQq8eSTT2LJkiUVtomLiwMAhIaGYsCAAWZ/TkRkfgqxC6iNE7c14DViRGRu+24UoZGXs9hl0D/UajUGDBhQ7XB58eLFSu+LiYlBXl5epfevWLECADBhwgSTc9oSke2R9EgtWw+IyBJOZrNX35H9+eef+P7776FSqTB+/HixyyGiKpL0SO2fvEiMiCzg71zHaGsyPB8pdgk25ZlnnkF+fj62bt0KrVaL1157DT4+PmKXRURVJO1Qe5uhlojMz1FCLZX31VdfQSaTITQ0FNOnT8eLL74odklEVA3SDrVsPyAiCzh3h58tjqgq8+ESke2SbE9ter4Wt4p0YpdBRHYor8SAGwVascsgIqJqkGyoPc7WAyKyILYgEBFJi2RDLeenJSJL+juXLQhERFIi2VCbXsDWAyKyHI7UEhFJi2RDLfvdiMiSGGqJiKRFsqE2naGWiCyI7QdERNIi3VCbz/YDIrKcc+zbJyKSFMmGWrYfEJEl5Wj0KNFx3lIiIqmQcKjlSC0RWVZusV7sEoiIqIokGWqzinQo1nMEhYgsK6eYX56JiKRCksvksvWAiKwhR2PfI7VFWaMssl8X328tsl8iogeR5Ehtej5DLRFZHtsPiIikQ5Khlv20RGQNORp+1tiKs2fPYtKkSWjatCnc3d3h4uKCkJAQdOjQAZMmTcK6devELlGyZs+eDUEQMHv27Go9Li0tDYIgoEePHhapy1z27t2L2NhY+Pj4QCaTQRAEfPPNN2KXJXmCIEAQhGo/rkePHhAEAWlpaWavSZLtB+xzIyJrsPf2A6lYv349Ro0aBY1GA19fX0RHR8Pf3x/Z2dk4cuQIFi5ciFWrVmHIkCFil0o25vr160hISEBubi66dOmC8PBwyGQyNGzYUOzSyAIkGWqLtLxIjIgsj1+gxZeRkYHExERoNBpMmzYNc+fOhYuLS7ltDh06hLVr14pUofRNmjQJI0aMgJ+fn9ilmN1PP/2EnJwcjBo1CitXrhS7HLvy119/iV1CBdIMtZw7koisgD214tu0aRPy8vIQFBSE999/3+Q27dq1Q7t27axcmf3w8/Ozy0ALAJcvXwYANGrUSORK7E/jxo3FLqECSfbUMtQSkTWw/UB8GRkZAAB/f/9qP/ZhPX+V9fbde/uRI0cwePBg+Pn5QalUomnTpvjggw9gMFT8PZSUlGTs17xw4QLGjh2LunXrQqlUokGDBnjttdeg0WjKPSYxMRGCIODtt9+utM7Vq1dDEAR07Nixys99x44d6NevH+rUqQMnJyd4e3ujUaNGGDNmDHbv3l1u24f11CYnJ6NDhw5wc3ODj48P4uPjsWfPnofWcP36dbzwwgto0qQJ3NzcoFar0aFDByxYsABabc0u+F61ahViYmLg4+MDpVKJevXq4emnn8aZM2fKbffNN99AEAS8/vrrAIA5c+YY3w/h4eFVOlZ4eDgEQcDFixfxww8/oEuXLvDw8IBarUaPHj2wZcuWctvr9XpERERAEATs27ev0v0+//zzEAQBL774ovG2e987x48fx/DhwxEYGAi5XG78dykpKcGKFSswevRoNG7cGB4eHnB1dUVUVBSmTJmC69evmzzeve/n/fv3IyEhAb6+vlCr1ejevXu5f8tt27YhJiYG3t7eUKlU6NOnDw4fPmxyvw/6+bpy5QqefvppBAYGwsXFBY0aNcKrr76KwsLCSl8Xc5BmqGX7ARFZAUdqxRcWFgYAOH78OFJTU6167O3bt+ORRx7BqVOn0KdPH3Tu3BlnzpzB9OnT8Z///KfSxx05cgStW7fGnj170L17d3Tr1g3p6el48803MWLEiHLbTp06FQCwePFi6HSm210WLlwIoLRNoCqWLVuG2NhYbN68GfXr18eQIUPQrVs3eHh4YNWqVVi/fn2V9lNWX2JiIg4fPowOHTogLi4OV65cQY8ePbBhw4ZKH7d79240b94cH374IYqKitCnTx9ER0fj3LlzmDx5MhISElBSUvWlqA0GAxITEzFy5Ejs3r0bbdq0weDBg+Hi4oKvv/4abdq0wbZt24zbN2zYEImJiWjVqhUAoFWrVkhMTERiYiKGDh1a5eMCwCeffILBgwdDo9Ggb9++aNq0KXbt2oWEhAR8+umnxu1kMpnx32jBggUm93Xnzh0sX74cMpkMzz//fIX79+7di/bt2+O3335Dt27dkJCQALVaDaD0C97YsWOxefNmeHt7Iz4+Hr169UJeXh4+/fRTtG7dGn///Xelz2Pz5s3o2rUr0tPT0adPHzRs2BC7d+9Gnz59sHfvXixcuBAJCQkoKipCbGwsgoODsWPHDnTv3v2B+73fqVOn0L59e3z99dcQBAH9+/dHZGQkPvzwQ8TExKC4uLjK+6ouSbYfcOEFIrKGEn7WiG7gwIEIDg7GtWvX0KdPH3Tv3h0xMTFo27YtOnToUKMR3Kp65513sHjxYowfP9542//+9z/07t0bCxYswPTp0xESElLhcR9//DFeffVVzJkzB3K5HEBpKO/UqRM2bNiAffv2oXPnzgCAtm3bIjo6Gr/++itSUlIwaNCgcvs6fvw4du/eDX9/fwwfPrxKdc+ZMwcGgwF79uxBly5dyt2XmZmJa9euVWk/mzdvxieffAJ3d3ds3boVXbt2Nd739ttvY8aMGSYfd+PGDQwePBg5OTlYtGgRxo8fD5msdAwtKysLTzzxBH766Se8/fbbmDVrVpVq+fzzz5GcnAw/Pz/8/PPPaN26NYDSsDtnzhzMmTMHI0eOxJkzZ+Dv748uXbqgS5cumD17No4ePYqBAwdWe3aHMh999JFxhLTM999/j5EjR+KFF15Az5490bx5cwDAuHHjMGvWLKxduxbz589HnTp1yu0rOTkZeXl56Nevn8kR4y+++AIvv/wy3nzzTeNrVsbT0xM//vgj4uPj4ezsbLy9pKQEr7/+Ot5++21MnToVmzdvNvk8PvjgAyQnJ2PMmDHG26ZNm4b58+fj6aefxrVr1/DTTz8hJiYGAKDT6TB8+HCsW7cO7777Lr744osqvV5PPvkkMjMz8cQTT2DZsmXGHvjLly+jV69eOHfuXJX2UxOSHKnVmzjtQ0RkbtWfrIbMTaVSITU1FY888ggMBgPS0tIwc+ZMJCQkICAgAG3atHngKGdtDB48uFygBYBevXohLi4OOp0OO3fuNPm4du3a4Y033jAGWgBo3rw5xo4dC6C0NeBeZaO1ZSOy9yob8XvmmWegVCqrVHdGRgY8PT0rBFoAxtesKj766CMApSPE9wZaAHjllVeMwdLU47KysjBx4kRMmDChXDjz9fVFcnIynJycsGDBApNtHKaU9VPPmjWr3HHLWgxatmyJnJycKgev6hgwYEC5QAsAw4cPx+DBg6HVavHJJ58Yb/f09ERiYiKKi4tN1vKwUffIyEjMnTu3QqAFALVajf79+5cLtADg5OSEt956C0FBQdi2bRvu3r1rct9Dhw4tF2gB4NVXXwUAnD59GhMmTDAGWgCQy+XGLy5VPUvy66+/4uDBg3B3d8eiRYvKXdQZFhZWaV+8uUgy1DLSEpE1MNTahqioKOzfvx8HDhzArFmzEBcXZxyhPXLkCCZMmID4+Hizn9bs16+fydubNGkCAJWOePbt29dkr2Fljxs0aBBCQ0ORmpqKU6dOGW/Pzc3FihUrIJfLMWHChCrX3bFjR+Tm5uLJJ5/EoUOHoNdXv41Gq9Xil19+AYAKQajMk08+afL2spHCykaWg4OD0ahRI9y8eRNnz559aC1Xr141ju4lJiZWuF8QBDz11FMAUOkXjdowdcx7b7+/J3vKlCkQBAGff/55ud7hsn/fqKgo9OnTx+Q+Bw4cWO7LkClHjx7F/PnzMXnyZDz99NNISkpCUlIStFot9Hp9pa0Cjz/+eIXbfHx84OvrW+n9ZRfYVdave7+y1yI+Pt6433sNGDAAnp6eVdpXTUgz1DLVUjV91uk0Pmp96uEbEt2jBvOKkwV17NgRc+bMwbZt25CRkYFDhw4Ze1R37NiBjz/+2KzHK+vnvZ+HhwcAoKioyCyPUygUxv7Ke3sxly1bhvz8fPTv3x+hoaFVrnvRokWIiIjA8uXL0b59e3h5eSEmJgZvvvmmcTaAh8nKyjLWWb9+fZPbVHb7+fPnAQBdu3Y1Xkx0/5+TJ08CAG7evPnQWsq+BPj6+hpfw/s1aNCg3Lbm9LDnf/Xq1XK3R0VFITY2FlevXi3Xd1w2Slt2oZgpD7qILT8/H4MHD0br1q0xbdo0LFiwAF9//TWWLVuGZcuWITMzE0Bp364plb0vVSpVpfeX9fPef4FjZcpei8pes+pcqFcT0gy1YhdAkpIQko3EeusxyP8Quvpki10OSQgzre0SBAFt27bFd999h/79+wPAAy9cMuVhI5imTgFXRU0e9+yzz8LV1RXJycm4e/cuDAYDFi1aBKDqF4iVadKkCU6fPo3Nmzdj2rRpaN68Ofbs2YPXXnsNjRo1wooVK6pdX3WUva5Dhw41XpxV2R9To3lSY6qF4v6WkitXriAlJQUqlQpJSUmV7svV1bXS+1555RX88MMPaNy4MTZs2IBr165Bo9HAYDDAYDAY+7Qra+l42Puypu93WyLJC8U4UktV5a8swbfRayBAAw/3XHxQ71t0zXkOGv2DT+8QAYCMQ7WSEBsbi5SUFNy6davc7U5OTigpKcHdu3eNI073unTpkrVKfChfX1+MHj0aX375JZKTkxEZGYnTp0+jadOm6NWrV7X3p1Ao8PjjjxtPKd+5cwfz58/HnDlzMH78eAwaNAju7u4PrEepVEKj0eDixYto1qxZhW0uXrxo8rGhoaE4e/YsXnrpJbRv377atd8vODgYQOno8Z07d0yO1paNDpdta04XLlwwzqJwr7Lnb+piwfj4eERGRiItLQ0nTpzAt99+C51Oh7Fjx1Y62vwwq1evBlB6kVrLli0r3F+VVg5LK3v9K3tvAJb9uZNkLHeW8xcNVc3u+FQ4o7QXyEWZCWf9bSxt/ovIVZFUKPlZI7qqXEhUdkr9/nBR9gvW1MpHx44dw5UrV8xQoflMmTIFQOnoXlkbwsSJE82ybw8PD8yePRteXl4oKCioMK/r/RQKBaKjowGg0pW4li9fbvL2xx57DMD/hbDaCgkJMbYXfPPNNxXuNxgMxtt79uxplmPeq7LnmZycDKB0Htj7CYKAyZMnAwDmz5+PL7/8EkD1R93vdfv2bQBAvXr1Kty3ffv2Cl/qxNC9e3cApfPdltV7r5SUFOTk5Fjs+JIMtZ7OkiybrOyLR/9CuMv+crd5eIcgUrsRTwSli1QVSYkLQ63oFi1ahMTEROzdu7fCfQaDAevXrzcGwPvngO3duzeA0imu7u0JvHjxIhITE6t85b21tGjRAr169cJff/2FlJQUeHh4VHoxVmUKCgowf/58k72qe/bsQU5ODuRyucnRxfv9+9//BgB8+umnFV7/efPmVTop/3//+194eXlh/vz5+OCDD0xewHfhwoVqtUFMnz4dAPDGG2/g6NGjxtsNBgPmzp2LI0eOwMvLC88++2yV91lVP/zwA1atWlXutrVr12LdunVQKBTG8Hq/pKQkeHp6YunSpcjMzETPnj3RtGnTGtdRdqHhvXPjAqUzFzz33HM13q85de3aFW3btkVeXh4mTpxY7ufuypUrxn9HS5FkOvRSSrJssqKBYbcxOvSHCrd7qPWAQYeXApbD18lyE0CTfeBIrfhKSkqQnJyM6OhoBAQEIC4uDqNHj0ZCQgIiIiIwZMgQFBQUYMyYMRg3bly5x86YMQNeXl7YsmULIiMjMXToUHTv3h1NmzaFn58fHn30UZGeVeXKRmuB0qvryy7iqari4mJMmzYNdevWRevWrTFs2DCMGjUKjz76qHEU7dVXX63S/L79+vXDxIkTkZeXh65du6Jnz54YNWoUmjdvjldeecXYN3q/kJAQ/Pjjj/D29sb06dMRGhqKmJgYjBkzBv369UPDhg0RERFR6QIFpowfPx5jx47FrVu30L59e/Tu3RujRo1CkyZNMGvWLLi6uuLbb7+1yLzFU6dOxciRI9GxY0eMHj0anTp1wrBhw6DX6zFv3jyTrQBA6QVYZbMyALUbpQWA119/HYIgYObMmWjZsiVGjhyJmJgYtGjRAhERETbzfl6+fDn8/f2xatUqREREYPjw4ejXrx8aN24MX19fY++vJUgyHXo6sx+SKlfHpRjJnVdDQMXQ6upyHTK5K/SadKxosc3Eo4n+j4uCoVZs48aNw4YNGzB58mTUr18fJ0+exJo1a7Bz507I5XKMHDkSW7duNa7SdK/69etj7969GDx4MO7evYtNmzYhIyMDr776KrZs2QInJyeRnlXlYmJiIJfLIQhCjVoPVCoVFi9ejOHDh0Oj0eDnn3/Ghg0bkJmZicGDByM1NRVz5syp8v4WLFiApUuXok2bNti/fz+2bNmCwMBApKamYuDAgZU+rlu3bjhx4gRmzpyJkJAQHDx4EGvWrMGRI0dQp04dvP7669WaU1YQBCQnJ+Pbb79Fly5dcOjQIaxduxYFBQVISkrCH3/8YWx7MLepU6di9erVUCgUSElJwfHjx9G1a1ds3LjxgSvLAUBcXByA0j7jAQMG1KqOwYMHY9euXYiJiUF6ejpSUlKQmZmJ2bNnY+vWrTbzfm7atCl+//13JCUlQafTYcOGDTh58iQmT56M1NTUCvPsmpNgsLXzL1Ww9txdDNvO08dk2umBmxGmPFjp/VevBSEnq7THbpVmIj4439BapZHEvPmIL2a0k/7V2ZUpyhplkf26+H5rkf06gi+//BLPPvssYmNjsX37drHLcWjh4eG4dOkSLly4UONpqMaMGYOVK1firbfewiuvvGLeAqkCSY7UerGnlirxdfSJBwZaAFB7/N+3xFHuK9DIvcDSZZFEeSl5VoisJz8/H2+//TaA0uVLSdr+/PNPfP/991CpVBVWpiPLkOSUXvxFQ6YMC8/CiJAND93O3S0TEOSAQQe9NhdLo9ah6+Gxli+QJCfQzb4/aziiahvee+89HD9+HL/88gvOnz+P+Ph4xMbGil0W1dAzzzyD/Px8bN26FVqtFq+99hp8fHzELsshSHLIk7Mf0P3qupbgq0dWAyh56LYKeQFU6v+bEsWl8DA+bPKHBasjqarrJsnv/SQxmzdvRnJyMu7cuYOkpCR8+y2/bEjZV199hdWrV8PLywtvvPEGXnzxRbFLchiS/MTm7Ad0v1/itsEJGVXe3sPTA3n3rCTYVbYaXX3Csee2twWqI6kKZKglK0hLSxO7BDLhQQsIPIgEL1WyG5JMh16c/YDusbzrnwhWHqrWY1SqnHL/b9AX4YN630Ip05mxMpK6QHd+1hARSYUkQ62TXIArp9ohACPq38LQoJRqP87ZKRsuboHlbhOK/uZqY2TkpZRBKZfkRyQRkUOS7Cd2HVeOoDi6ILdifNGxan20pnh41alwW2RJCkYEXa9lZWQP2HpARCQtkg21DTwtN3kvScMvcdugQGaNH69SFZq4VY//BqzgamNk9zMfEBHZG8mG2oYetrFyBonju27HEOhset3xqnJV3oDCybPC7VxtjADOfEBEJDXSDbWeDLWOamyDTAwMrH4f7f0EAfDwDjN5n1/hTkyPOFvrY5B0sf2AiEhaJBxq2X7giMJUGixqvxqA1iz7U6srv2+k+0pEueeb5TgkPZz5gIhIWiQcajlS64h2x26FArfMtj9313QIMtNfkPTaXHwVtd5sxyJpqa/mZwwRkZRINtQ28HQCJ/VyLGt7HEEdpyNm3adMVgIPr4hK71dytTGH1cJXKXYJRERUDZINta4KGYLc2fPmKJIaZiKhzkaL7Fvt4fLA+7vKvkc339sWOTbZJjeFgAY8G0REJCmSToUNPZ1wLd88vZVku+qrirCg3fcALLPal8otE6Xf7/Qm7zfoNXg/7Dt0zX4OGj37LB1BU29nyAT7Pxf0+84Ei+y3fc/NFtkvEdGDSHakFmBfrSMQYMCuuC2QI8tix1Ao8uGuDn1wHUV/42uuNuYwWrL1wOacPXsWkyZNQtOmTeHu7g4XFxeEhISgQ4cOmDRpEtatW1fhMeHh4RAEARcvXrR+wSYIggDBBr8s1bSuHj16QBAEpKWlmb8oM9FoNJgxYwYaNWoEpVIJQRAQHh4udlmSN3v2bAiCgNmzZ1frcWlpaRAEAT169LBIXRIfqeUMCPZufc8/4K84ZvHjqD19kH/30gO3aVSSghFBjbDqepDF6yFxsZ/Wtqxfvx6jRo2CRqOBr68voqOj4e/vj+zsbBw5cgQLFy7EqlWrMGTIELFLJRszc+ZMvPfee6hTpw4GDBgANzc3+Pn5iV0WWYikQ21zH4Zae/ZMZAbiA6xzGlOtuoMbD92qdLWxHbf+jVvFfO/ZM4Za25GRkYHExERoNBpMmzYNc+fOhYtL+T74Q4cOYe3atSJVKH1//fWX2CVYzOrVqwEAe/bsQaNGjUSuxn5MmjQJI0aMsLkvCJIOtY/UefAFPiRdDdRF+KiN5fpo76d0vgWlSwA0RQ9edlevSceK5tsQf7i/VeoicbTgF2absWnTJuTl5SEoKAjvv/++yW3atWuHdu3aWbky+9G4cWOxS7CYy5cvAwADrZn5+fnZXKAFJN5T6++qYF+tHRJgwK7YTZDDujMOeHgFVmk738Kd+G8DrjZmrwJc5QjgamI2IyMjAwDg7+9fq/3s3LkTsbGx8Pb2hqurK9q2bYvk5GST2166dAnvvvsuevXqhbCwMCiVSnh5eaFLly74/PPPodebvqgUAPbt24fHHnsMXl5eUKlUaN++PZYuXWpy23PnzkEul8Pb2xsFBQWV7rNZs2YQBAFbtmyp0nPNzc3Fa6+9hhYtWsDd3R1KpRJBQUGIjo7GrFmzUFJSUm77B/XUXrlyBU8//TQCAwPh4uKCRo0a4dVXX0VhYeFD61i7di3i4+Ph7+8PZ2dnBAcHY8yYMTh58mSVnsf9rl69ismTJ6NRo0ZwcXGBp6cnoqOj8fnnn0OnKz8AUtZPbTAYyj1HQRDwzTffPPRY33zzDQRBQFJSErKysjBx4kTje6FevXr4z3/+g+zs7HKP+frrryEIAuLi4ird7/Xr1+Hk5ARXV1dkZZVeK3Lx4kVjr69Op8P8+fPRpk0bqFSqcv8uJ0+exOuvv47o6GgEBwfD2dkZvr6+6N27t3FE+n739rBqNBrMmTMHkZGRcHFxQVhYGF566SUUFRUBKH3fTJ8+HREREXBxcUF4eDhmz54NrbbiBfkP66lNTk5Ghw4d4ObmBh8fH8THx2PPnj0PfM3NQfKf3J3ruODv3JKHb0iSkdLrEHwVx61+XJW6BDcf3oMAABjhthIp7v/F6Xx3yxZFVsfWA9sSFla6lPXx48eRmpqKmJiYau9j6dKlmDt3Ltq2bYv4+HhcvHgR+/fvR2JiIm7fvo1///vf5bZfvnw5Zs6cifr16yMyMhLR0dFIT0/Hvn378Ouvv+Knn37C2rVrKwTBNWvWYOTIkdDpdGjevDlatGiBK1eu4JlnnsGJEycq1NWgQQMkJCRg48aNWLlyJZ599tkK2+zcuRMnT55EgwYN8Nhjjz30uRYUFKBLly44fvw4/P39ERMTA3d3d9y4cQOnTp3C3r178cILL8DLy+uh+zp16hS6d++OzMxMBAYGon///sjPz8eHH36InTt3Vvo4rVaL0aNHY/Xq1VAqlWjXrh2Cg4Nx5swZrFy5EuvXr8f69esRHx//0BrKHDx4EPHx8bh9+zbCwsIwcOBA5ObmIi0tDXv37sUPP/yAlJQUODuXnmUZOnQobt26hWXLlgEAEhMTjftq2LBhlY+bnZ2NRx55BFlZWeUujPvoo4+wdetW7Nmzx/iFa9SoUXjppZfw888/48yZM4iMjKywv88//xxarRZjx46Fr69vufsMBgMGDx6Mbdu2oWvXrmjSpEm59838+fPx1VdfoXHjxmjRogW8vLxw+fJl7Ny5E6mpqdi/fz/mz59v8nkUFxcjLi4Of/zxB3r06IGoqCjs2bMH8+bNw8mTJ7Fs2TI8+uijuH37Nrp164ZGjRph9+7dmDNnDjIyMvDZZ59V+TWbOnUqPvnkE8hkMnTp0gVBQUE4duwYevTogcmTJ1d5PzUhGMq+xkjUouM5mLj7waeMSTomRN3A/NZLUNn0WpZkMAg49ZcWOm1elbbXuLZFl8NjLVwVWdu/W3rhwy4BYpdhFVKY0isvLw+NGzfGtWvXIAgCunfvjpiYGLRt2xYdOnR44AhueHg4Ll26BCcnJ6xfvx59+/Y13vfNN9/gqaeegqenJ9LT0+Hq6mq87+DBg3B1dUXz5s3L7e/69et4/PHHcfToUaxevRrDhg0z3nfjxg1ERkbi7t27mD9/Pv7zn/8Y70tNTUXfvn2NI2L3/trdsWMH+vTpg1atWuHIkSMVnsPQoUOxbt06fPDBB3jhhRce+nolJycjMTERjz32GH788Uc4Of3f2Uy9Xo89e/agc+fOxvAHwBjO748DHTt2xMGDB/HEE09g2bJlxl7my5cvo1evXjh37hyA0uB979Xsr776Kt566y088sgj+O6771C/fn3jfWvXrsWIESPg4eGB8+fPVylcazQaREVF4dKlS3juuefwySefGJ/X+fPnERMTg4sXL2LGjBl48803yz22suf2MGXvDwDo1KkTNm/eDB8fHwBATk4OEhISsHfvXowYMQLfffed8XGvvfYa3nzzTUyZMgUff/xxuX2WlJQgLCwMN27cwKFDh9C2bVsApSO1Za9RSEgIUlNTTQbiXbt2ITQ0FBER5RcMOn36NHr37o2rV6/iwIED6Nixo/G+tLQ09OzZE0Dpv+eWLVuMYfrSpUto06YNsrOz0aJFC4SHh2PVqlVwc3MDAPz+++/o3Lkz9Ho9Lly4YPyCCZSO1M6ZMwevv/56udHazZs3o2/fvnB3d8fWrVvRtWtX431vv/02ZsyYAQDo3r27RWbNkHT7AVA6Ukv2IcqzCO+3/h5iBFoAEAQDPLzrVXl7ZeFhfNT0sAUrIjGwV9+2qFQqpKam4pFHHoHBYEBaWhpmzpyJhIQEBAQEoE2bNli8eHGF08/3mjx5crlACwBJSUlo3LgxcnNz8fvvv5e7r0OHDhUCLQAEBQVh3rx5AEpHZe/11Vdf4e7du+jUqVO5QAsAMTExGD9+vMnaevfujWbNmuHo0aP45Zfy0wZevXoVP/74I9zc3PD0009X+vzuVdau0adPn3KBFgBkMhm6d+9eLtBW5tdff8XBgwfh7u6ORYsWlbs4LywsrNL+5tu3b+PDDz+Ei4sL1q1bVy7QAqUhffz48cjOzsaKFSuq9JzWrFmDS5cuISgoCB999FG55xUREWGs5dNPPzV+cTCnzz77zBhoAcDLywuLFy+GIAhYvXo1rl69arzv+eefh5OTE5YtW4b8/Pxy+1m3bh1u3LiBzp07GwPt/d566y2TgRYoDYL3B1oAiIqKwsyZMwGg0gsmBUHAV199VW50uF69ehg7tnRg5sKFC/jyyy+NgRYA2rdvj8ceewx6vb7KAfSjjz4CUHoh2b2BFgBeeeUVtG7dukr7qSnJh9qWvkq4K2xv3j+qHrmgx/96p0CG7IdvbEFqdfUWV+girOZqY3ZEANAr2O2h25F1RUVFYf/+/Thw4ABmzZqFuLg44wjtkSNHMGHCBMTHx6O4uNjk4/v162fy9iZNmgAArl27VuE+jUaDjRs3YtasWXjuuefw1FNPISkpCZ9//jmA0tGxe5X90h89erTJY917+vt+U6ZMAQAsWLCg3O1lp6pHjx5dpRFNoDSQA8C8efOQnJyM27dr9vlU9nzi4+MrnCYHgAEDBsDT07PC7Tt37kRhYaGx79OUslHdvXv3VquWESNGQKms2B40ePBgeHt74+7duzh06FCV9llVrVq1MhnEWrRogTZt2kCv12P37t3G24OCgjB06FDk5uZi+fLl5R6zcOFCAKWBrzIPm5YuLy8Pa9aswYwZM/Cvf/0LSUlJSEpKMs7TfP/7skxYWJjJL2plF9C1a9cOAQEVz1CV3X/9+vUH1gWUtp2UfTEbM2aMyW2efPLJh+6nNiTfUyuXCegQ4IK06w9vWifbtSnmEHwUNbt4wJzc3W5AEBQwGKq2Uh1XG7MvzXyceZGYDevYsaPx1KrBYMAff/yB9957D6tWrcKOHTvw8ccf47///W+Fx9172vReHh4eAFBhdG///v0YPny48cp5U+7cuVPu/8tG6+4fmSxT2e1AaQB4+eWXsX79eqSnpyMwMBDFxcX44osvADw4BN2vR48eeOmll/Dee+8hMTERgiCgUaNGiI6OxoABA9CvXz/IZA8fz3rY8ym7sOno0aPlbj9//jyA0paLhy3ocPPmzao8JeOXjgfVUr9+fWRnZ5v8glIbD/p3q1+/Pg4fPlxupBYo/ZLy3XffYeHChXjuuecAAMeOHcMvv/yCOnXqYOjQoSb3FxAQUG6k9H4bN27EU089ZbzAzJT735dlKvsZUKlUD7xfrVYDqPgzYkpWVpZxu5r8HJiD5EdqAaATTxdK2uQm19HDd6vYZQAA5DINVJ7V+6ErXW3M8ld1kuVxlFY6BEFA27Zt8d1336F//9Ip9jZs2GBy26qEuDIFBQUYOHAgLl++jKeeegq//fYbbt++Da1WC4PBYBwJM+flKG5ubnj22WdRUlKCJUuWACg9VZ2RkYGuXbuiZcuW1drfO++8g3PnzuGTTz7BsGHDkJ+fj6+//hoDBw5Ep06dKpwWN6eymSEaNmyIxMTEB/6pyUV/tuj+90KnTp3QsWNHHD9+HLt27QLwf6O0//rXvypt/7i3r/t+165dw/Dhw5GVlYUXX3wRR48eRW5uLnQ6HQwGA7Zv326yljIP+xmozs+ILbOLIYnOdV0BkU9bU8009SrEOy3F66M1xcPTHXdzqveYRiUbMTI4Et9d42pjUtYrhKFWimJjY5GSkoJbt27Vel+7d+9GRkYG2rZta3IqrrNnTU/nFxwcjFOnTlW6JO/DluqdOHEiPvjgAyxZsgQzZswwtiJUZ5T2XuHh4Zg8ebLxavODBw9izJgxOHjwIObNm4c5c+Y88PFlrQMPqvvSpYqrMIaGli45HhUVVaWps6qirJayUWBTLly4UG5bcynbryllr01ISEiF+6ZMmYIxY8ZgwYIFaNWqFVauXAmFQmEcua2ujRs3orCwEIMGDcK7775b4f7K3pfW5OvrC6VSCY1Gg4sXL6JZs2YVtrH0ktV2Ec071+VIrRTJBT1Se/8IGXLFLqUclXvlp3Yqp8d0/+Xwczbd00e2Ty4APYIqHykhcVRlRLSsTcBUuKiush7Uyk7HVnZxU/fu3QEAK1euNHl/ZXPilimbpur69euYNWsW9u7di6CgIAwePLiqpT9Qhw4d8PzzzwOAyVkW7lf2fLZt22ayLzclJQU5OTkVbo+JiYGzszPS0tKQmWmemYnKenC///57k6fBf/jhB2RnZ0OtVpt9EY5jx47h2LGKS7WfOHEChw8fhkwmQ7du3Src/8QTTyAwMBAbNmzAm2++ifz8fAwaNAhBQTUb+Cj7N6hXr+LFzAaDAd9++22N9mtOCoUC0dHRACr/Obi/z9jc7CLU+rsq0IwrAEnOtt6/wUt+SuwyKnBS3IGrKrTaj9NrbmBF820WqIisoa2/Ep5K9kXbmkWLFiExMdHkRUUGgwHr1683jmqOGDGi1scru3gsNTW1wiIBS5Yswffff2/ycePGjYNKpcK+ffvwySeflLsvLS0Nixcvfuixp06dCqC0fQAAxo8fD4WieidUf/jhB+zevbvCAhElJSXYtq3088lUMLpf165d0bZtW+Tl5WHixInQaDTG+65cuYLp06ebfFydOnUwefJk5Ofno1+/fvjzzz8rbKPRaJCSkoJTp6r2+T9s2DCEhYXh+vXreOGFF8otBnDhwgVMmzYNQOksF/cvoVxbBoMBEyZMKLfQQm5uLiZMmACDwYAhQ4YYR6fv5eTkhAkTJkCr1RpnZ6jpqDvwf+/LtWvXIj093Xi7TqczfgmyBWVzPn/66acVapo3bx4OH7bsjEF2EWoBIKEeJ8GXkheaXUMXn+1il1EpD8+KV/tWBVcbky7209qmkpISJCcnIzo6GgEBAYiLi8Po0aORkJCAiIgIDBkyBAUFBRgzZgzGjRtX6+O1adMGAwYMwN27d9GmTRvExcVh5MiRaNKkCZ577jnjPJv3CwoKwhdffAG5XI6pU6eiZcuWGDVqFLp3745evXpV6bRz165d0aZNGwCloehf//pXtevftWsXunfvjjp16iA2NhZjxozBgAEDEBISgm3btiE4OBgvvvhilfa1fPly+Pv7Y9WqVYiIiMDw4cPRr18/NG7cGL6+vujcubPJx73zzjsYNWoUfvvtN7Ru3Rpt27bF0KFDMWLECHTp0gW+vr4YMGBAlU9FK5VKrF27Fj4+Pvjss8/QsGFDjBgxAgkJCWjatCkuXLiAuLg4vP7661V9maqsf//+uHHjBiIiIjB48GAMGTIEERER2LNnDxo1alRhxop7jR8/3jhbQ8uWLU2O6FZVv3790K5dO1y9ehWRkZHo27cvhg8fjgYNGuDdd9/FSy+9VON9m1O/fv0wceJE5OXloWvXrujZsydGjRqF5s2b45VXXjF+cbMUuwm1j4cx1EpFc+8CvNF8NQDbXfdDrar5hRQj3FYiyt1yF2KQZTDU2qZx48Zhw4YNmDx5MurXr4+TJ09izZo12LlzJ+RyOUaOHImtW7di+fLlZrvYZc2aNXjvvfcQFRWFX375BT/99BPCwsKwfft2PPPMM5U+bsSIEUhLS0NcXBwuXbqEH3/8EXfv3sXixYsrXenpfrGxsQBK53OtW7dutWtPSkrCyy+/jMaNGxtfq3379iE0NBRvvfUWjh49WuU2jaZNm+L3339HUlISdDodNmzYgJMnT2Ly5MlITU2t9IInhUKBlStXYsuWLRg4cCAyMzORkpKC7du34/bt2+jXrx++/fbbaoW8Dh064MiRI5g4cSLkcjl++OEH7NmzB23atMFnn32GTZs2VWn+3ery9vY2zoZx8OBBbNq0Ce7u7pgyZQr2799vchqsMgEBAcbpwCZOnFirOhQKBdLS0jBjxgwEBwcjNTUVaWlpaNOmDfbt21et1dksbcGCBVi6dCnatGmD/fv3Y8uWLQgMDERqaioGDhxo0WNLfkWxMlq9Af5fn0OOxnYuOKKKnGR6XBn8PTzlpufSsyVnTitQrKlJfy2gcW2DLoctOx8fmY+zTED2uAZwc7Kb7/lVIoUVxRyJTqdDgwYNcOnSJezdu7fSkVCyvLIVxRITE2t8wduZM2fQuHFjeHp64tq1aw+crovMw24+wRUyAbG8ctnmbe99QBKBFgA8vGp+Fa2y8A+uNiYhneq6OFygJduzZMkSXLp0CZ07d2agtQOzZs0y9uQy0FqHXUzpVaZvuAqrz+WJXQZV4sXmV9HZ+yexy6gytYcOtzJq/vjS1cbCsTvL5+Ebk6gGhKvELoEc1OnTp/Hee+/hxo0b2LZtG2QyWaVL0JLtS0lJwY8//ogTJ07gwIEDqFu3bpV7mKn27CvU1nOHkwwoYQeCzWnrW4DXm30PW+6jvZ+rMh0yuSv0upqtVsfVxqRjaAPHDLVsExBfeno6vvrqKzg7O6NZs2aYPXs2Hn30UbHLoho6fPgwli5dCrVajd69e2P+/PlVXuKYas9uemrLxKZcxc9XC8Qug+7hJNPj2pDvoJZJb1aAq9eCkZNVu+V7/3YegJFHe5ilHjK/jgEuODDU9JykREQkHXbXRDY4wjFHXGzZjj77JBloAUDtUfuTGQ2LN2Jk8HUzVEOW4KijtERE9sbuQu3ACBVkgthVUJlXW15CR68dYpdRYyq3TECobesAVxuzZcMaqMUugYiIzMDuQm1dNwUerculLm1Be988vNpkDaTUR3s/ubwQKo+Hr77zMHrNDaxottUMFZE5dQxwQbiHk9hlEBGRGdhdqAWApCgPsUtweEq5Dlt7bYAA6c9G4eHpaZb9+BalcbUxGzMmkqO0RET2wi5D7YhGaqg556So/he7FyrZ32KXYRZq9+yHb1RFXG3MdihkpZ8VRERkH+wy+bk7yTCSv6xEM6vVJbT1+J/YZZiNk1M2XNyCzLIvvTYXX0WtM8u+qHZiQ9zh72pXsxoSETk0uwy1APBsU/OcMqbqecQvDy83lnYfrSkeXpWv711dysI/8DFXGxPdmCh+8SUisid2G2rbB7igtZ9S7DIciqtch8291ttFH+391Oois+4vWliNbr63zbpPqjpvpYyriBER2Rm7DbUA8EwTjtZa0864X+EunBe7DItwcU6HwtnLbPsrW21MKdOZbZ9Udc808YQb++6JiOyKXX+qj45Uw1XBSWutYW6bC2iltp8+2vsJAuDhFWrefRb9jW9a7DbrPunh5AIwqYWX2GUQEZGZ2XWo9VLKObG6FUQH3MELkWvELsPiPNTm7xNuWLyJq41Z2aAIFcLUnJuWiMje2HWoBXjBmKW5y3VI6bEeAgrELsXi3FzTIZOZu09bj+l+yVxtzIqmtvQWuwQiIrIAuw+1XQJd0cTbWewy7FZa/G64CRfFLsMqZDIt1F7hZt+vvjiDq41ZSTt/JboEcsVBIiJ7ZPehFgCmtvQSuwS79E67c2iu2iV2GVal9rBMIPItSsOLDc5YZN/0fzhKS0Rkvxwi1D7V2BMh7pxk3Zy6172DKQ3Xil2G1ancMmGpH5vhbivRWMXVxiylrpscwxuyx56IyF45RKh1lgt4sQ1HaMxF7aTDD93WQkCh2KVYnUKRD3d1mEX2rdfewZeRXG3MUp5r5gVnOWdDISKyVw4RaoHSC8bquMrFLsMu7IpLg6twWewyROPhabkvSFxtzDKUcgHPNeNFo0RE9sxhQq2LQobprTlaW1vvt/8bTdz3iF2GqFTqXIvuP1pYjR5cbcysRjdSo44bW5CIiOyZw4RaAJjQ3At+LhytramYwFw838Dx+mjvp3TKgtK1jsX2b9Br8F7Yt3DhamNm4SwTMKuDr9hlEBGRhTlUqHV3kuE/rbzELkOSPJ20WNt1LQQUiV2KTfDwqmvZAxSdw9dcbcwsnmvmiXpcbIGIyO45VKgFSpfH9FY63NOutd3xaXARrohdhs1Qqyy/WAJXG6s9lZOA19r7iF0GERFZgcOlOw9nOaZw3fdq+bjjWUS6/SJ2GTbF1SUdcoWlp4fiamO19UIrb/i7speWiMgROFyoBUonYFc7OeRTr7bYoBw8W5/TTN1PEAzw9K5n8ePoizOwsjlXG6sJPxc5prfmKC0RkaNwyGTn7SLHy205E8LDeDtrsZp9tJVSe1hnzlOfwjS8xNXGqu3Vdj5QOzvkRxwRkUNy2E/8aa290cCDF488yO74/0GJq2KXYbPcXG5AEKzzHnqCq41VSz21AhOac15aIiJH4rChVimX4aMu/mKXYbMWdjqNhq57xS7DpsnlxVB5hlvlWFxtrHpmd/CFUu6wH29ERA7JoT/1+4ar8HiYu9hl2JzHQ7LxVL31YpchCR6e1nv/KAv/wCdND1nteFLVzMcZT0Z5iF0GERFZmUOHWgD4qIs/nGVcD76Mn7IE30WvgQCN2KVIgso9C4D13j+PcrWxh5rX2Q8ygT/TRESOxuFDbSMvZy7IcI/d8TvgDM6NWlVOijtwU4VY7XgGfTFXG3uA4Q3VeLyeSuwyiIhIBA4fagHgtfa+CHLn8rmfdz6F+i4HxC5Dcjy8/Kx7wKJz+IarjVXgrZThY/bJExE5LIZaAConGd7r7Ni/DAeE3sbYMPbR1oTK/a7Vj9mgeBNGBV+z+nFt2fuP+qOOGxdaICJyVAy1/xgV6YEuga5ilyGKOi7FSH50DQRw5aqacFHehLPS18pH1WOa33IEcLUxAECvYFc83YRTeBEROTKG2nss6BoAhQO+IqV9tOlilyFpHl7BVj+mvjgDy7naGFzkAj7vUUfsMoiISGQOGOEq18pPiRltHWtZzaXRJxCm/E3sMiRP7SHOhVtcbQx4vYMvGno6i10GERGJjKH2Pq+180Vbf6XYZVjFkHpZGBmyQewy7IKby3XI5W6iHNuRVxtr5avE9NZc8pqIiBhqK3CSC0iOqQul3L7nuazrWoKvO60GUCJ2KXZBEPRQe4WLcmxHXW1MJgBf9KgDBeeZJiIiMNSa1MxHif/X0doX/ljXnrjtcEKG2GXYFbWHk2jHdsTVxqa29EKHOi5il0FERDaCobYS01t7o1uQfc6GkNz1OEKUv4tdht1Rud8ABPHmO35UWI2eDrLaWCtfJd7uZOX5gYmIyKYx1FZCJghYEVMX3kr7eomG17+FYUE/il2GXZLLiqDyCBft+AZ9MeY5wGpj7goBq2IDoZTb188mERHVDn8rPECo2glf2NFUQUFuxfiyI/toLcnDUy1uAQ6w2tinXQPQ2JuzHRARUXkMtQ8xpIEa45p4iF2GWeyJ2wYFMsUuw66p3bPFLsGuVxsb1UiNp7jIAhERmcBQWwUfdwlAYy9pjwx92+1PBDkfFrsMu+fklAMXN+svxFCefa42FunlhMXd7efMCRERmRdDbRW4O8nw4+NB8JJof+3oiJsYFMg+Wmvx9PIXu4R/VhvbInYZZuOuELA+PghqZ2n+DBIRkeXxN0QVRXo54/s+gZDa9LWh7hos7rAagFbsUhyGSlUgdgkAAJ/CXXaz2tiSHnXQzMcxFkUhIqKaYaithtgwd7z/qPijcNWxO3YrFLgpdhkOxUWZASdnL7HLAGAfq41NbO6JUZH20ddORESWw1BbTf9u5Y2nG0vjF+zq7kdQ1/mI2GU4HEEAPLxCxS4DQOlqY19FrhW7jBrrXMcF86MDxC6DiIgkgKG2Bj7rXgfRdW17JaPEhpnoV3ej2GU4LLWHQewSjJwLj+DTptJbbKORpxNSHg+Gs9R6foiISBQMtTXgLC+9aCVMpRC7FJPCVRosbLcagH1Pwm/L3FzSIZPZzhefzsIaSa02FuAqx7a+wfBzFW+FNiIikhaG2hoKcFMg5fFguCtsbRTJgF2xmyHHLbELcWgymRZqr3CxyzCS0mpj7goBmxOCEeEp7Wn0iIjIuhhqa6GVnxLJMXVhS7F2fc8jCHA6JnYZBEDtaTsjtQD+WW1sl9hVPJBcAFbHBaJ9gI29dkREZPMYamtpcAM13u3sJ3YZAIBnGmXgsYBNYpdB/1C5ZcDWfsQaFG/GGBtebWxx9zp4vJ5K7DKIiEiCbOs3rkT9t40PXm/vI2oNDdRF+Kjt92Afre1QyAvg7hEmdhn30eM/Nrra2Mz2PnimKZfAJSKimmGoNZPZHf3wUhtvUY4twIC02E2QQzoXAjkKD09x3hMPYourjT3V2AP/r6NtnPEgIiJpYqg1o3c6+2NqSy+rHzel1yH4KY5b/bj0cGr3HLFLMMmncBdebmgbq43FhbphSY86YpdBREQSx1BrZh91CcC/rHgKdXzUDfT232q141H1ODvfhtLVNgPbMNcVaKrOE7WGPiFu+OGxIChktnS5JRERSRFDrQUs7h6AJ6Msv+pYpEcRPmjNPlpb5+FVV+wSTNJr7+KLRutEO37feu7YmBAEVwU/hoiIqPb428QCBEHA0p51MLyh2nLHgAE7+2yEHNkWOwaZh1ptexdllRFrtbEhESqsjw+CUs6PICIiMg/+RrEQuUzAit51MbC+u0X2vznmd/goTlhk32RersrrUDhZ7gtObVl7tbFRjdT4PjYQTlz+loiIzIih1oIUMgHfxwZhSIR5592c3OQ6evqxj1YqBAFQe9UTu4xKla42ttIqq4093dgDy3vXhZw9tEREZGYMtRbmLBewOi7QbLMiNPEsxDstVwPQm2V/ZB0eHjb+o1Z0HsssvNrY88098WXPOpAJDLRERGR+Nv6b1j7IBAEfdQnA+4/61WpJXbmgx//6pECGHHOVRlbi7poOQeYsdhkPFGHB1camtfLGwm51IDDQEhGRhTDUWtG01j74rk8glDXsJdza+yC85H+ZuSqyBpmsGGrPcLHLeAjLrDY2s70P3o/2N+s+iYiI7sdQa2XDG6mxvW8wvJTVe+n/0/Qauvpss1BVZA0eHm5il/BQ+uIMrGi+2Sz7UsoFJMfU5UphRERkFQy1Iuge7IZfB4UiVKWo0vbNvQswt8VqAAbLFkYW5e5+E6hVA4p1eBfurvVqY3Xd5Ng1MARjrTBfMxEREcBQK5qmPkrsHxKGlr4P7rN0kumxI+ZHyJBrpcrIUpwUeXBThYpdRpXUZrWxdv5K/D40DI/UcTVzVURERJVjqBVRkLsCewaFIja08tPS23ofgKf8tBWrIkvy8PIRu4QqKV1tbC2Eap4dGN5QjT2DQhGscrJQZURERKYx1IrMw1mOrX2DMaOtT4UT0/9tdhWPev8kSl1kGSpVzUY/xeBceBSfNjtUpW0FAHM7+mJVbCCXvSUiIlHwt48NkAkC3uzkh5THg4wXkLXyzsfs5t+DfbT2xcX5JpyV0rlwqhPWIMbvwauNqZwErI8Pwqvtfa1UFRERUUUMtTakb7gKh4aGoaO/E37q/SNkuCt2SWQBHt5BYpdQZQZ9Md4JrXy1sfoeTvh1UBgGmnnVPCIioupiqLUxEZ7O2DckGN6u0rigiKpPrdKKXUL1VLLa2MhGahx5Igwt/ZQiFEVERFQeQ60Nksmc4aQaByfVVECw/blNqXrcXNMhV7iLXUa1RBRvxtiQ0tXG1E4yLOtVF9/2CYSHs1zkyoiIiEoJBoOBTZs2TK/LREneIhi0tZs3lGzLteshyL51QuwyqkXmHICZWa/ik+5haOBp20v+EhGR42GolQCDQQ9d0VZoC9YAMO8SpiSOO3n1cPn8MbHLqDJBUCCw3nAE1hsOQcbRWSIisj0MtRKi16WjJO9zjtraAZ3eBadOZMFgsP3+Whf3eqjf5AW4qxuKXQoREVGlGGolpnTUdhu0BavBUVtpu3jJH3m5f4tdxgPIUCd0EIIjxkIm42IKRERk2xhqJap01HYJDFquNiZVt3MicP3yH2KXYZKbOhJhkc9B5REldilERERVwlArYQaDHjrNztJRWwPntJWaYq0nzpy8LHYZ5SicvBDSIBG+dftAEO5f446IiMh2MdTaAYM+D9rCddAV7QBgepJ8sk3nzqlQmH9N7DIgCHL4B/dFUP3RUEhsujEiIiKAodau6LVXoS1YBn2JtKaKcmQ3s+oj49oRUWtQe7VCWOR4uLrXE7UOIiKi2mCotUM6zUFoC1bAoL8pdin0EIWaOjh3WpzZLJyV/ghp+Ax8ArqIcnwiIiJzYqi1UwZDceksCYWbAEOe2OVQJQwG4MxpGUqKs612TJlMiTqhg1C33jDI5S5WOy4REZElMdTaOYOhELrCrdAWbQEMBWKXQyakZ4QhK+NPix9HJlPCP/hx1A0bAidnb4sfj4iIyJoYah2EQV8AbdEW6Iq2MdzamLyCUFz8+7jF9i/InOEf9BgCw4bCSeljseMQERGJiaHWwRj0ef+E2+2AoVDscgiAXq/Aqb/yodcVmXW/Mrkr/IPiUSd0MJwZZomIyM4x1Doogz4POk0qtEU/A/rbYpfj8K5cDULu7b/Msi+FkwcCQvojILgvFE5qs+yTiIjI1jHUOjiDQQd98W/QFm2FQWvLS7bat5y74bh64Wit9qF0DUJAcF/4BcXxAjAiInI4DLVkpC/5G9qibdAXHwAXcbAurc4Vp05kAtBX63GCzAne/tHwC4yD2qsFVwEjIiKHxVBLFRj02dAWpUKv2cO5bq3o4kUf5N25UKVtXdzrwT8wDr51e7HFgIiICAy19AAGgwEG7SnoNL9AV3yAsyZYWFZ2BNKv/FHp/TKZEt4B3eAfFAeVZxMrVkZERGT7GGqpSgyGYuiLD0Gn2QN9yZ9ge4L5FZf44Mxf94/UCnD3iIRv3d7wrdMDcoWbKLURERHZOoZaqjaDPhe64gPQFx+CvuQvAFqxS7IbZ8+6QlOUCbVnc3j7Pwov/85wVvqJXRYREZHNY6ilWjEYCqEv/hO6ksPQFx8BDHfELkmiXCBzboFibXso3VvCydlT7IKIiIgkhaGWzMZg0MOg/Ru64sPQlxyFQXcZAN9epgkQ5GGQOTWFzKk1ZE5NIAgKsYsiIiKSLIZashiDvgB67RnotaegLzkNg/Y8gBKxyxKJHIKiPmSKxpA5NYZMEQVB5i52UURERHaDoZasxmAogUF7DvqSU9Brz0KvvQgYssUuyzJkvpDJw/4JslGQOTWCIHBBBCIiIkthqCVRGfR3oNdegkF3GQbdNeh1V2HQXQMMhWKXVkVKCIpQyOShpe0EijAI8jCOwhIREVkZQy3ZJIMuCwb9TRj0WaV/dFkw6G/BoL8Ng/4WYMi3UiUuEOR+EGS+EGR+EOT+pX//8wcyLwiCzEq1EBERUWUYakmSDIYiQH8XBkMhYCio5O/iex4h3Pc3AMggCK6AzA2C4AYI9/7t/s/trlZ8VkRERFRTDLVEREREJHk8b0pEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESSx1BLRERERJLHUEtEREREksdQS0RERESS9/8BFU2p5zk9orUAAAAASUVORK5CYII=",
|
||
"text/plain": [
|
||
"<Figure size 640x480 with 1 Axes>"
|
||
]
|
||
},
|
||
"metadata": {},
|
||
"output_type": "display_data"
|
||
}
|
||
],
|
||
"source": [
|
||
"from matplotlib.patches import Patch\n",
|
||
"\n",
|
||
"colors = ['#0095D9','#F7EC59','#CBBE4A'] # Color Picker helps\n",
|
||
"\n",
|
||
"plt.pie(\n",
|
||
" [0.8, 0.15, 0.05], # Try and Error ratios\n",
|
||
" colors=colors,\n",
|
||
" startangle=-55\n",
|
||
")\n",
|
||
"\n",
|
||
"plt.legend(\n",
|
||
" labels=[\"Sky\", \"Sunny side of pyramid\", \"Shady side of pyramid\"],\n",
|
||
" # Set right color and size for Patches\n",
|
||
" handles=[Patch(facecolor=color) for color in colors],\n",
|
||
" handlelength=1,\n",
|
||
" handleheight=1,\n",
|
||
" # Move Legend to the right\n",
|
||
" loc=\"center left\",\n",
|
||
" bbox_to_anchor=(1, 0.5),\n",
|
||
" fontsize=16,\n",
|
||
" # Disable background and edge\n",
|
||
" facecolor='none',\n",
|
||
" edgecolor='none'\n",
|
||
")\n",
|
||
"\n",
|
||
"plt.tight_layout() # Layout shouldnt Overflow\n",
|
||
"\n",
|
||
"plt.show()"
|
||
]
|
||
}
|
||
],
|
||
"metadata": {
|
||
"kernelspec": {
|
||
"display_name": "Python 3 (ipykernel)",
|
||
"language": "python",
|
||
"name": "python3"
|
||
},
|
||
"language_info": {
|
||
"codemirror_mode": {
|
||
"name": "ipython",
|
||
"version": 3
|
||
},
|
||
"file_extension": ".py",
|
||
"mimetype": "text/x-python",
|
||
"name": "python",
|
||
"nbconvert_exporter": "python",
|
||
"pygments_lexer": "ipython3",
|
||
"version": "3.11.6"
|
||
}
|
||
},
|
||
"nbformat": 4,
|
||
"nbformat_minor": 5
|
||
}
|